رگرسیون خطی چندگانه (Multiple Linear Regression) برای پایگاه های داده مبتنی گراف – به زبان ساده


در این نوشته به شما نشان خواهیم داد که چگونه میتوانید با استفاده از یک مجموعه رویههای تعریف شده از سوی کاربر، یک مدل رگرسیون خطی با چندین متغیر مستقل برای مجموعه دادههایی در خصوص املاک برای اجاره کوتاهمدت بسازید. چنین رگرسیونهایی بنام رگرسیون خطی چندگانه نامیده میشوند.

هدف ما در این نوشته آن است که از یک فهرست املاک برای اجاره کوتاهمدت استفاده کرده و بتوانیم هزینه اجاره هر شب یک اتاق را تخمین بزنیم. با این حال مسلماً موارد زیادی هستند که بر روی قیمت اجاره چنین املاکی تأثیر میگذارند. برای نمونه نزدیک بودن یک ملک به مکانهای توریستی میتواند تأثیر زیادی بر روی ارزش آن داشته باشد. در شکل زیر برخی عواملی که میتوانند بر روی قیمت تأثیر داشته باشند را به نمایش گذاردهایم.

با توجه به این که در فهرست فوق ما آدرس خانهها را نداریم امکان تجزیه و تحلیل مکان ملک نسبت به مقاصد گردشگری آستین دشوار است. اما در عوض میتوانیم از رابطه (:Review)-[:REVIEWS]->(:Listing) استفاده کنیم. همه املاکی که در فهرست ما حضور دارند، دستکم یک بررسی از سوی کاربران داشتهاند. اینک کمی عمیقتر دادههای خود را بررسی میکنیم و از تعداد بررسیهای هر ملک، علاوه بر تعداد اتاقها برای تخمین قیمت شبانه آن استفاده میکنیم.
توجه داشته باشید که همه این تحلیلها جنبه آموزشی دارد و توجیه آماری واقعی برای تصور این که تعداد بررسیهای کاربران میتواند بر روی قیمت یک ملک تأثیر بگذارد در دست نیست. این کار به طور عمده بدین دلیل صورت میگیرد که نشان داده شود چگونه میتوان یک مدل با چند متغیر مستقل ایجاد کرد. همچنین مشاهده تعداد نظرات هر ملک و کمّیسازی بازخوردهای مثبت و منفی کاربران نیز میتواند در این خصوص راهگشا باشد.
پیشزمینه
پیش از آن که بخواهیم به بررسی بازار املاک اجارهای آستین بپردازیم، برخی جزییات مهم رگرسیون خطی چندگانه را بررسی میکنیم. به خاطر داشته باشید که در رگرسیون خطی ساده قصد ما این است که متغیر وابسته یعنی y را با استفاده از مقدار یک متغیر منفرد مستقل به نام x پیشبینی کنیم. اما در رگرسیون خطی چندگانه قصد بر این است که از متغیرهای چندگانه مستقل (x1, x2, …,xp) برای پیشبینی متغیر وابسته y استفاده شود.
درک بصری رگرسیون خطی چندگانه اندکی دشوارتر است و به تعداد متغیرهای مستقل (p) بستگی دارد. اگر p=1 باشد، رگرسیون چندگانه به یک رگرسیون خطی ساده تبدیل میشود و نقاط دادهای (x1,y) بر روی یک سیستم مختصات دوبعدی استاندارد (با محورهای x و y) قرار میگیرد. رگرسیون خطی را که بیشترین برازش را بر روی همه دادهها دارد مییابد.

اگر p=2 باشد، نقاط دادهای (x1,x2,y) در یک سیستم مختصات 3 بعدی (با محورهای x، y و z) قرار میگیرد و رگرسیون خطی چندگانه صفحهای که بیشترین برازش را روی همه نقاط دادهای دارد مییابد.

برای تعداد بالاتری از متغیرهای مستقل، درک بصری این نوع رگرسیون حالتی انتزاعی دارد. در مورد تعداد p متغیرهای مستقل، نقاط دادهای (x1, x2, x3 …, xp, y) در یک فضای p+1-بعدی قرار دارند. آنچه واقعاً مهم است، این است که مدل خطی (که p-بعدی است) را میتوان به وسیله p+1 ضریب β0, β1, …, βp نشان داد به طوری که y به وسیله معادله y = β0 + β1*x1 + β2*x2 + … + βp*xp تخمین زده شود.
انواع مختلف رگرسیونهای خطی چندگانه
میبایست توجه کنید که دو نوع رگرسیون خطی چندگانه وجود دارد، یکی کمترین مربعات معمولی (OLS) و دیگری کمترین مربعات تعمیم یافته (GLS) است. تفاوت اصلی بین این دو نوع آن است که در OLS فرض میشود همبستگی قوی بین هیچ دو متغیر مستقل وجود ندارد. GLS با متغیرهای مستقل همبسته سروکار دارد و در آن ابتدا دادهها تبدیل میشوند و سپس از OLS برای ساخت مدلی از دادههای تبدیل یافته استفاده میشود.
هر دو رویههای فوق از OLS استفاده میکنند. از این رو برای ساخت یک مدل موفق ابتدا باید در مورد رابطه بین متغیرها به خوبی اندیشه کنید. شاید درست نباشد که تعداد اتاق خواب bedrooms و فضای موجود accommodates را به عنوان دو متغیر مستقل از هم در نظر بگیریم چون مشخص است که تعداد اتاقهای خواب یک بنا با فضای موجود آن همبستگی کامل دارند. از سوی دیگر رابطه منطقی روشنی بین تعداد نظرات و تعداد اتاقهای خواب یک بنا وجود ندارد. برای تحلیل کمّیتر میتوانید متغیرهای مستقل را طوری انتخاب کنید که هر جفت ضریب همبستگی پیرسون نزدیک به صفر داشته باشند.
کاربرد عملی رگرسیون خطی چندگانه
اینک زمان آن رسیده است که با استفاده از یک سری کوئری یک مدل رگرسیون خطی چندگانه را در Neo4j بسازیم.
راهاندازی
ابتدا باید فایل jar آخرین نسخه رگرسیون خطی را دانلود و نصب کنید. به این منظور دستور زیر را در مرورگر Neo4j وارد کنید:
:play http://guides.neo4j.com/listings
سپس کوئریهای مهم را دنبال کنید تا بتوانید فهرستی از املاک اجاره کوتاهمدت را بسازید. برای راهنمایی بیشتر در خصوص نصبNeo4j و نصب رگرسیون خطی چندگانه و وارد کردن مجموعه داده املاک اجارهای آستین میتوانید به این آدرس مراجعه کنید.
افراز دادههای تمرینی و تست
زمانی که مجموعه دادهها وارد شدند و رویهها نصب شدند، میبایست این مجموعه داده را به دو بخش 75:25 درصد (تمرینی: تست) افراز کنیم. بدین منظور از مدل نهایی که در این آدرس معرفی شده است، استفاده میکنیم و 75 درصد آن را به صورت Train: برچسبگذاری میکنیم.
MATCH (list:Listing)-[:IN_NEIGHBORHOOD]->(:Neighborhood {neighborhood_id:'78704'})
WHERE exists(list.bedrooms)
AND exists(list.bathrooms)
AND exists(list.price)
AND (:Review)-[:REVIEWS]->(list)
WITH regression.linear.split(collect(id(list)), 0.75) AS trainingIDs
MATCH (list:Listing) WHERE id(list) in trainingIDs
SET list:Train
سپس برچسب:Test را به 25 درصد باقیمانده اضافه میکنیم.
MATCH (list:Listing)-[n:IN_NEIGHBORHOOD]->(hood:Neighborhood {neighborhood_id:'78704'})
WHERE exists(list.bedrooms)
AND exists(list.bathrooms)
AND exists(list.price)
AND (:Review)-[:REVIEWS]->(list)
AND NOT list:Train
SET list:Test
کمّیسازی همبستگی
اگر مایل باشید که همبستگی پیرسون بین متغیرهای مستقل را بدانید، میتوانید از تابع regression.linear.correlation(List<Double> first, List<Double> second) استفاده کنید. یکی از ورودیهای List<Double> برای این تابع شامل مجموع «تعداد بررسیها» از فهرست بندیهای زیاد است و هر «تعداد بررسی» از طریق تجمیع روابط از فهرستها به دست میآید. امکان اجرای دو سطح از تجمیع در یک کوئری وجود ندارد (collect(count(r))). از این رو باید دو کوئری را اجرا کنیم.
ابتدا یک مشخصه num_reviews را روی فهرست مجموعه دادهها ذخیره میکنیم.
MATCH (:Review)-[r:REVIEWS]->(list) WHERE list:Train OR list:Test WITH list, count(r) AS num_reviews SET list.num_reviews = num_reviews
سپس دادههای (num_reviews, rooms) را از همه فهرستها جمعآوری کرده و همبستگی را محاسبه میکنیم.
MATCH (list) WHERE list:Test OR list:Train WITH collect(list.num_reviews) as reviews, collect(list.bedrooms + list.bathrooms) as rooms RETURN regression.linear.correlation(reviews, rooms)

ضرایب همبستگی پیرسون در محدوده [1,1-] هستند و 0 به معنی عدم همبستگی است. 1 نشاندهنده همبستگی کامل و 1- به معنی همبستگی منفی است. تعداد بررسیها و تعداد اتاقها همبستگی برابر با 0.125- دارند که نشاندهنده همبستگی منفی ضعیفی است. OLS روش قابل قبولی برای این همبستگی ضعیف محسوب میشود و از این رو میتوانیم با این مدل کار خود را به پیش ببریم. در مورد تفسیر ضرایب همبستگی در این آدرس بیشتر میتوانید بخوانید.
راهاندازی مدل
در این مدل رگرسیون از متد create استفاده میکنیم، چارچوب کار به صورت ‘Multiple’ خواهد بود و تعداد متغیرها نیز برابر با 2 است.
CALL regression.linear.create( 'mlr rental prices', 'Multiple', true, 2)
افزودن دادههای تمرینی
دادههای معین را به همان قالبی که در رگرسیون خطی ساده عمل میشود به کل اضافه میکنیم. کافی است یک مدخل دیگر (تعداد بررسیها) به فهرست خود از متغیرهای مستقل اضافه کنیم.
MATCH (list:Train) WHERE NOT list:Seen CALL regression.linear.add( 'mlr rental prices', [list.bedrooms + list.bathrooms, list.num_reviews], list.price) SET list:Seen RETURN count(list)
تمرین دادن مدل
ما میبایست مدل خود را تمرین دهیم به طوری که پارامترهای خط (βi)، ضرایب تعیین (R²) و موارد دیگر پیش از پذیرش دادههای تست یا انجام پیشبینی به دست آیند. اگر این گام را فراموش کنید و سپس تلاش کنید تا دادههای تمرینی را به مدل اضافه نمایید و یا پیشبینی انجام دهید، در این صورت مدل شما به طور خودکار ابتدا تمرین میبیند.
CALL regression.linear.train('mlr rental prices')
توجه کنید که پس از فراخوانی رویه train نیز میتوانید دادههای تمرینی بیشتری به مدل اضافه کنید. تنها کاری که باید انجام دهید این است که پیش از تست کردن مدل جدید، یک فراخوانی دیگر به train بفرستید.
افزودن دادههای تمرینی
عملکرد مدل را بر اساس دادههای مشاهده نشده تحلیل کنید و به خاطر داشته باشید که وقتی دادههای تست را اضافه میکنید یک پارامتر اضافی به نام ‘test’ به عنوان ورودی برای رویه regression.linear.add مورد نیاز است.
MATCH (list:Test) WHERE NOT list:Seen CALL regression.linear.add( 'mlr rental prices', [list.bedrooms + list.bathrooms, list.num_reviews], list.price, 'test') SET list:Seen RETURN count(list)
تست مدل
اینک که همه دادههای تست اضافه شدند، میتوانید رویه test را برای محاسبه اندازهگیریها (در testInfo در ادامه) فراخوانی کنید. این کار به شما امکان میدهد که عملکرد مدل خود را تجزیه و تحلیل کنید.
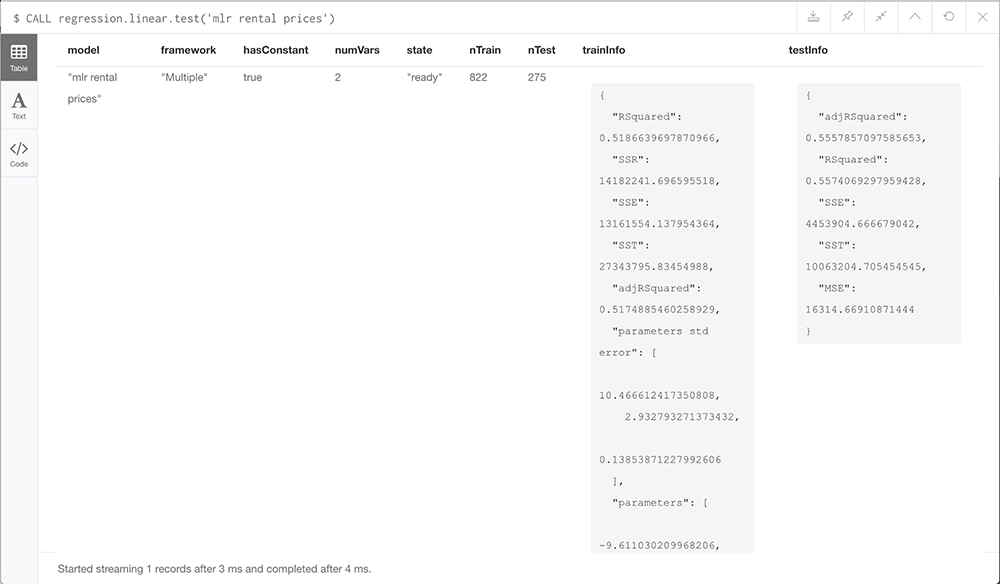
CALL regression.linear.test('mlr rental prices')
همچنین میتوانید هر زمان از طریق فراخوانی رویه Info اطلاعاتی در مورد مدل به دست آورید.
CALL regression.linear.info('mlr rental prices')
اجازه بدهید نگاهی به R2 تعدیل یافته داشته باشیم. این مقدار مشابه R² در رگرسیون خطی ساده است اما تعدیل یافته است زیرا که متغیرهای مستقل به مدل اضافه شدهاند و از این رو R² تعدیل یافته افزایش نمییابد مگر این که مدل بیش از مقدار تصادفی افزایش یابد. از این رو وقتی مدل رگرسیون خطی ساده خود (با دو متغیر مستقل) را با مدلهای رگرسیون ساده خطی مقایسه میکنیم، میبینیم که R2 تعدیل یافته اندازهگیری بهتری ارائه میکند.
ما معمولاً به دنبال مقادیر R² تعدیلیافتهای بالاتر از 0.6 هستیم؛ اما مقادیر نزدیک به 1 برازش خطی بهتری را از خود نشان میدهند و در این مدل مقدار R² تعدیل یافته تمرینی برابر با 0.517 و مقدار R² تعدیل یافته تست برابر با 0.556 است. مدلی که با استفاده از رگرسیون خطی چندگانه ساختهایم کمی بهتر از روشهای رگرسیون خطی ساده عمل میکند.
یک گام به پس
سؤالی که اینک به طور جدی مطرح میشود این است که یادگیری ماشین و هوش مصنوعی چه جایگاهی در پایگاههای داده گراف دارند؟ چند پاسخ به این سؤال وجود دارد؛ اما هیچ یک آز آنها پاسخ «صحیح» محسوب نمیشوند. قبلاً مشخص شده است که چگونه میتوان یک مدل یادگیری ماشین ساده را بر مبنای دادههایی در قالب گراف ایجاد کرد و از اکسپورت کردن دادهها به نرمافزارهای دیگر اجتناب نمود. در این مقاله جنبه جالب دیگری ظهور مییابد: توانایی ساخت مدلهایی با دادههایی که ذاتاً در ساختار گراف ذخیره شدهاند. ما میتوانیم روابط «تعداد بررسیها» را به راحتی در هر فهرست استخراج کنیم. در این زمینه پایگاههای داده گراف، باعث افزایش انواع دادهای میشوند که میتوان به سادگی برای ساخت مدلهای یادگیری ماشین مورد استفاده قرار داد.
اگر بخواهیم از این هم جلوتر برویم، میتوانیم بررسی کنیم که چگونه مدلهای یادگیری ماشین میتوانند به طور مؤثری برای استفاده از ساختارهای گراف مجموعه دادهها جهت یادگیری و انجام پیشبینی مورد بهرهبرداری قرار گیرند.
خلاصه
در این بخش فهرست خلاصهای از ترفندهایی که برای استفاده از رویههای regression.linear.* در رگرسیون خطی چندگانه مورد نیاز است را ارائه کردهایم:
- تعیین نوع مدل “Multiple” در طی regression.linear.create.
- تعیین تعداد متغیرهای مستقل در طی regression.linear.create.
- عدم استفاده از متد regression.linear.remove برای دادههای تست یا تمرینی.
- شما نمیتوانید دادههای تمرینی را با استفاده از regression.linear.copy از یک مدل به مدل دیگر کپی کنید.
- شما میتوانید مدل را پیش از تست، تجزیه و تحلیل یا پیشبینی با یک فراخوانی به regression.linear.train تمرین بدهید.
- از adjusted R² برای مقایسه دقیق مدلها با تعداد مختلفی از متغیرهای مستقل استفاده کنید.
- regression.linear.data پارامترهای مدل را باز میگرداند و نه سریالسازی بایتی [] آن. از این رو نمیتوانید از regression.linear.load استفاده کنید.
اگر به این نوشته علاقهمند بودید، احتمالاً موارد زیر نیز مورد توجه شما قرار خواهند گرفت:
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مدل سازی، برازش و تخمین
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزشهای نرمافزارهای آماری
==