گراف در علوم کامپیوتر – راهنمای مقدماتی
گرافها در همه وجوه زندگی ما حضور دارند؛ اما احتمالاً آن چنان که باید با آنها آشنا نیستیم. از نظر بسیاری از توسعهدهندگان خودآموخته، مفهوم گراف دشوار به نظر میرسد. به همین جهت، ممکن است درک گرافها برای توسعهدهندههای باتجربه و فارغالتحصیلان علوم رایانه که با آنها کار نکردهاند، دشوار باشد. اما واقعیت این است که گراف روشی جذاب و ضروری برای بازنمایی اطلاعات و روابط در دنیای پیرامون ما محسوب میشود. ما میتوانیم از گرافها برای انجام کارهایی بسیار جذاب به وسیله رایانه استفاده کنیم. الگوریتمهای گراف ابزارهای زیادی برای درک شبکهها و رابطههای پیچیده ارائه میکنند. در این مقاله مقدماتی، شما را با مبانی گراف در علوم کامپیوتر آشنا میکنیم. ناگفته نماند که با مفاهیم پیچیده، دشوار یا ریاضیاتی سر و کار نخواهیم داشت و صرفاً مفاهیم مقدماتی را معرفی میکنیم.
انگیزه بحث راجع به گراف در علوم کامپیوتر
پیش از آن که وارد مباحث نظری گراف بشویم، در این بخش برخی انگیزههایی که ممکن است برای یادگیری گراف مورد نیاز باشد را ارائه میکنیم. در واقع به این سؤال پاسخ میدهیم که گرافها چه هستند و با آنها چه میتوان کرد؟
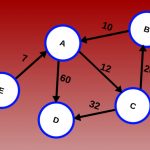
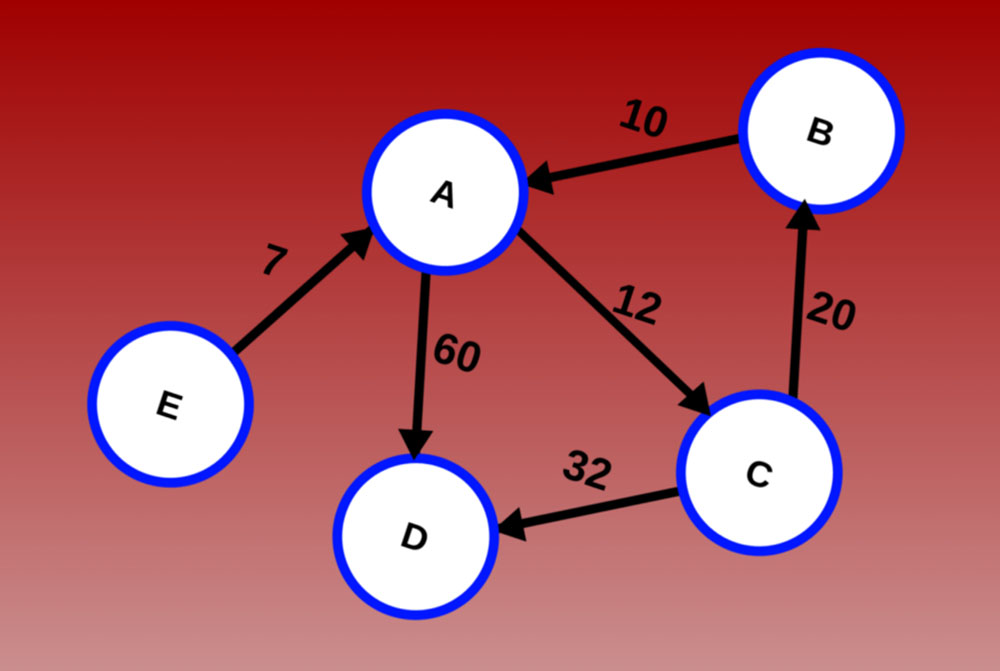
گراف در بنیادیترین شکل خود گروهی از نقطهها است که با خطوطی به هم وصل شدهاند.
این همان تصوری است که باید در ذهن خود داشته باشید. همه مفاهیم پیچیدهای مانند (G(V, E که در کتب درسی ارائه میشوند صرفاً روشی برای بیان همان مفهوم انتزاعی اتصال نقطهها به هم با استفاده از خطوط است.
ما از گرافها برای مدلسازی روابط در دنیای واقعی استفاده میکنیم. برای نمونه:
- Google Maps از یک سری نقطهها و خطوط برای مدلسازی شبکه جادهها استفاده میکند و مسیری برای رسیدن به مقصد نهایی به شما معرفی میکند.
- شبکه دوستان فیسبوک یک گراف است که در آن هر فرد یک نقطه به حساب میآید و رابطه دوستی بین افراد نیز به صورت خطوط نشان داده میشود.
- اینترنت یک گراف عظیم است که صفحههای وب نقطه هستند و لینکهای بین صفحات، خطوط ارتباط آن محسوب میشوند.
ما میتوانیم شیءهای فضای فیزیکی، روابط بین افراد و ساختارهای سند را با استفاده از گرافها یعنی نقطههای ساده و خطوط ارتباط آنها نشان دهیم.
زمانی که روابط مدلسازی شدند، موارد زیر در اختیار ما خواهند بود:
- یافتن کوتاهترین مسیر بین دو نقطه
- شناسایی گروههای رابطهها
- ذخیرهسازی دادهها و ایجاد لینکهایی بین تقریباً هر نوع چارچوب (برای مثال لیستهای پیوندی و درختها)
گرهها، رأسها و یالها
زمانی که دانشمندان رایانه در مورد گراف صحبت میکنند، از واژههای نقطه و خط استفاده نمیکنند. به جای آن به هر نقطه، یک گره یا رأس و به هر خط، یک یال یا کمان گفته میشود. متداولترین اصطلاحها رأس و یال هستند. زمانی که میبیند فردی برای نمایش گراف از نماد (G(V, E استفاده میکند، در واقع منظور وی این است که گراف G دارای مجموعه رأس V و مجموعه یال E است.
جهتدار یا غیر جهتدار
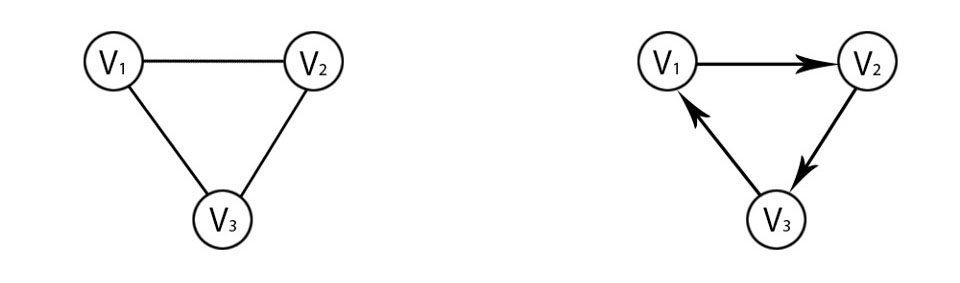
مهمترین مزیت گوگل مپ این است که وقتی مسیری را اشتباه میروید به شما هشدار میدهد. برخی اوقات یالهای یک گراف باید به یک جهت اشاره کنند. در چنین مواردی آن گراف، به نام گراف جهتدار نامیده میشود. از فلشهایی برای نشان دادن جهت یالهای گراف استفاده میشود تا همگان متوجه جهت یالهای گراف بشوند.
توییتر یک گراف جهتدار است، زیرا روابط در آن تنها در یک جهت حرکت نمیکند. شما در توییتر میتوانید فالوورهای زیادی داشته باشید؛ اما لزومی نیست که همه آنها را نیز فالو بکنید. به طور عکس رابطههای دوستی در فیسبوک یک گراف غیر جهتدار هستند. زمانی که فردی با یک فرد دیگر دوست میشود، این رابطه دوطرفه است و در رابطه جهتی وجود ندارد. جهت اشاره به وضعیت یال از اصطلاحهای زیر استفاده میشود.
- مبدأ یک یال (head) رأسی است که یال از آن خارج میشود.
- مقصد یک یال (tail) آن رأسی است که یال به آن وارد میشود.
گرافهای دوری یا غیر دوری
اگر یک گراف غیر جهتدار شامل حلقهای باشد که با دنبال کردن آن از میان یالها بتوان به نقطه شروع رسید، در این صورت آن را گراف دوری مینامیم.
اگر یک گراف جهتدار حلقهای داشته باشد که بتوان با دنبال کردن برخی یالها در جهت صحیح به نقطه آغاز بازگشت. در این صورت آن را گراف دوری مینامیم.
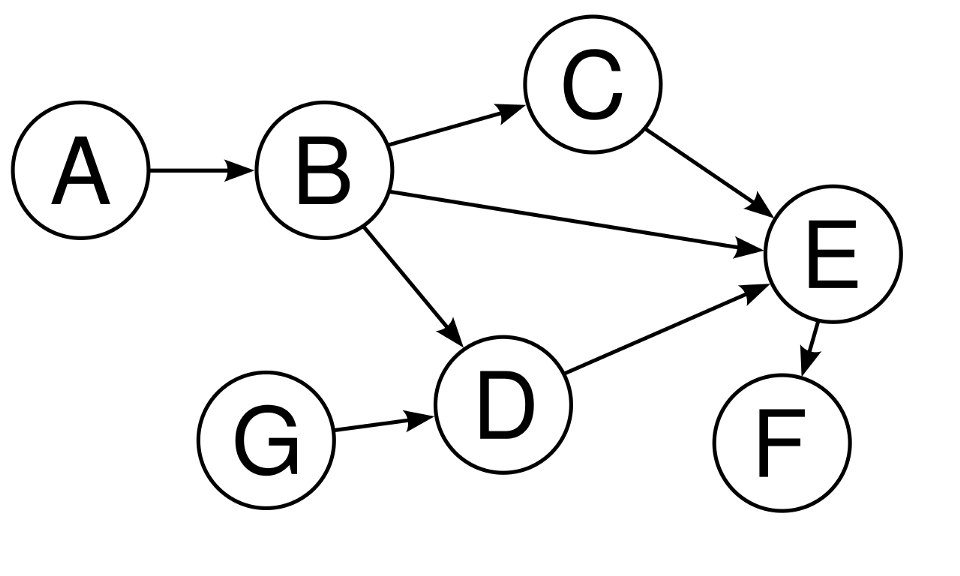
از سوی دیگر، یک گراف غیر دوری هیچ حلقهای ندارد. برای نمونه گراف زیر غیر دوری است، زیرا هیچ حلقهای ندارد. با این که همه رأسها کاملاً به هم متصل هستند؛ اما تنها در یک جهت میتوان حرکت کرد.
یالهای وزندار
اگر بخواهیم هنگام یافتن کوتاهترین مسیر محاسبات دیگری را نیز در این فرایند وارد کنیم، میتوانیم برای هر یک از یالهای گراف یک وزن تعیین کنیم.

گوگل هنگام محاسبه مسیر بین مبدأ تا مقصد از وزن دهی برای محاسبه مواردی مانند ترافیک استفاده میکند. انتزاعهای زیادی برای مفهوم یال وزندار میتوان تصور کرد. وزن میتواند نشان دهنده شدت، مسافت، دشواری یا مطلوبیت باشد.
مسائلی که میتوان با گراف حل کرد
تا به این جای مقاله با برخی واژهها و اصطلاحات مرتبط با گراف آشنا شدیم؛ اما گراف میتواند مسائل مختلفی را در علوم رایانه حل کند. برخی از الگوریتمهای مطرح گراف را در ادامه ملاحظه میکنید.
- وجود یک مسیر بین دو نقطه
- یافتن کوتاهترین مسیر
- یافتن بهترین نقطه شروع
- ایجاد کوتاهترین برش (تقسیم یک گراف به دو قطعه از طریق برش کمترین تعداد یالهای ممکن)
- پیمایش عمق-اول و عرض-اول کد گراف قابل دسترس از یک رأس مفروض
- جستجو/درج کردن/حذف کردن از یک درخت
- جستجو/درج کردن/حذف کردن از یک لیست پیوندی
- یافتن بیشترین گردش
این الگوریتمها میتوانند به حل مسائل زیر کمک کنند:
- ساخت یک حلکننده پازلهای سودوکو
- یافتن راهحلی برای بحث بین دوستان در مورد کمترین مقداری که باید پرداخت شود.
- تعین مسیرهای تحویل کارآمد
- ساخت یک موتور جستجو
- ایجاد یک اپلیکیشن دوستیابی آنلاین هوشمند
سخن پایانی
در صورتی که مشغول ساخت هر چیز پیچیدهای توسط رایانه باشید به احتمال زیاد مجبور خواهید بود از گراف استفاده کنید. امیدواریم این راهنما مقدماتی توانسته باشد شما با را مبانی گراف آشنا سازد.
این راهنما به هیچ وجه یک راهنمای جامع محسوب نمیشود و چه بسا دانشجویان دکترا که همه عمر خود را صرف مطالعه گرافها کردهاند. به یک معنا و از جهات مختلف رشته علوم کامپیوتر را میتوان هم ارز با مطالعه گراف دانست.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای علوم کامپیوتر
- آموزش نظریه گراف و کاربردها
- مجموعه آموزشهای مهندسی نرم افزار
- گراف — ساختار داده و الگوریتم ها
- نظریه گراف (Graph Theory) در علوم کامپیوتر – به زبان ساده
- آموزش گراف در ساختمان گسسته
- آموزش رنگ آمیزی گراف در نظریه گراف و کاربردها
- گراف — تعاریف و انواع به زبان ساده
==













یکی از کاربرد گراف ها در شجره نامه های خانوادگی است.