مجموعه فازی (Fuzzy Set) — به زبان ساده

شاید با اصطلاح منطق فازی (Fuzzy Logic) در نوشتار منطق فازی (Fuzzy Logic) و کاربردهای آن — به زبان ساده آشنا شده باشید. در آنجا اشاره کردیم که رویکرد منطق فازی را می‌توان به شکلی تصور کرد که به جای در نظر گرفتن دو وضعیت مثلا سیاه یا سفید، طیفی از رنگ خاکستری را جایگزین نتایج منطقی کرد که از یک طرف به رنگ سفید و از طرف دیگر به رنگ سیاه محدود می‌شود. اگر همین ایده را برای تعریف مجموعه‌ها و اعداد نیز به کار ببریم، مجموعه فازی و اعداد فازی ایجاد خواهند شد. در این نوشتار به بررسی مجموعه‌ های فازی و خصوصیاتشان خواهیم پرداخت و در مورد شیوه ترکیب این مجموعه‌ها نیز بحث خواهیم کرد.

برای آشنایی با مفهوم مجموعه و اعضای آن بهتر است نوشتار مجموعه ها در ریاضیات – مفاهیم پایه را مطالعه کنید. همچنین برای شیوه استفاده از گزاره‌ها و روابط بین گزاره‌ها خواندن مطلب گزاره ها و سورهای منطقی — به زبان ساده خالی از لطف نیست.

مجموعه فازی (Fuzzy Set)

همانطور که می‌دانید، مجموعه، گردایه‌ای از اشیا است. هر یک از اشیا درون مجموعه را یک عضو (Element) می‌نامند. به این ترتیب مشخص است که یک مجموعه با اعضای آن تعیین می‌شود. معمولا مجموعه‌ها را با حروف بزرگ و اعضای آن را با حروف کوچک لاتین نشان می‌دهند.

فیلم آموزش کنترل فعال سازه با رویکرد فازی با میراگر ATMD در فرادرس

کلیک کنید

برای نشان دادن تعلق یک شئ به یک مجموعه از علامت $$\in$$ استفاده می‌کنیم. برای مثال اگر بخواهیم نشان دهید که شئ $$x$$ در مجموعه $$A$$‌ است از عبارت ریاضی زیر کمک می‌گیریم.

$$\large x \in A$$

و می‌خوانیم «$$x$$ در $$A$$‌ است» یا «$$x$$ عضو $$A$$‌ است». همچنین اگر شئ در مجموعه $$A$$‌ نباشد، از عبارت $$x \notin A$$ استفاده می‌کنیم و می‌خوانیم «$$x$$ در مجموعه $$A$$ قرار ندارد» یا «$$x$$ عضو $$A$$‌ نیست». حال فرض کنید برای نشان دادن عضویت یک شئ در مجموعه $$A$$ از یک تابع استفاده کنیم. به این ترتیب اگر تابع نشانگر $$\mu_A(x)$$ بیانگر تعلق شئ $$x$$ به مجموعه $$A$$ باشد، آنگاه خواهیم داشت:

$$\large \mu_A(x)=\begin{cases}1 & x \in A\\0 & x \notin A \end{cases}$$

در این حالت تابع $$\mu_A(x)$$ را تابع عضویت مجموعه $$A$$ می‌نامیم. برای مثال اگر $$A=\{1,3,5,7\}$$ آنگاه مقدار تابع عضویت برای $$x=5$$ برابر با $$\mu_A(5)=1$$ ولی برای $$x=2$$ به صورت $$\mu_A(2)=0$$ است. ولی در منطق فازی، شیوه نمایش تابع عضویت متفاوت است. در ادامه به بررسی تابع عضویت و در نتیجه معرفی مجموعه‌های فازی می‌پردازیم.

مجموعه‌ فازی و تابع عضویت (Fuzzy Set and Membership function)

در منطق فازی به جای استفاده از یک تابع نشانگر به عنوان تابع عضویت مجموعه $$A$$ از یک تابع با شرایط زیر استفاده می‌شود. فرض کنید در اینجا $$\mu(x)$$‌ تابع عضویت فازی باشد.

• اگر $$x$$ شامل مجموعه فازی $$A$$ نباشد، آنگاه $$\mu(x)=0$$. در این حالت $$x$$ عضو $$A$$ نیست.
• اگر $$x$$ به صورت جزئی شامل مجموعه فازی $$A$$ باشد، آنگاه $$0<\mu(x)< 1$$. دراین حالت $$x$$ را عضو فازی می‌گوییم.
• اگر $$x$$ عضو قطعی مجموعه فازی $$A$$ باشد، آنگاه $$\mu(x)=1$$. مشخص است که باز هم در این حالت $$x$$ عضو فازی نامیده می‌شود.

بنابراین به نظر می‌رسد برای مشخص کردن مجموعه فازی $$A$$ باید از دو مولفه استفاده کرد به این معنی که ابتدا عضو و سپس درجه عضویت آن عضو را نام برد. به همین علت مجموعه‌های فازی مثل $$A$$ را به صورت زوج مرتب $$A= (U,\mu)$$ نشان می‌دهند که مولفه اول اعضا و مولفه دوم نیز درجه عضویت را نشان می‌دهد. هنگامی که مجموعه $$U$$ متناهی باشد، معمولا مجموعه فازی $$A$$ را به صورت زیر نشان می‌دهند.

$$\large A=\{\frac{\mu(x_1)}{x_1},\frac{\mu(x_2)}{x_2},\frac{\mu(x_3)}{x_3}, \cdots, \frac{\mu(x_n)}{x_n}\},\;\;\;x_1,x_2\cdots,x_n \in U$$

مشخص است که منظور از کسرها، اعداد کسری نیست.

نکته: گاهی مجموعه فازی را به صورت زیر نیز نشان می‌دهند. باز هم باید دقت شود که منظور از علامت +، جداسازی اعضا از یکدیگر است، همچنین کسرهای نیز به معنی کسر عددی نیستند.

$$\large A=\dfrac{\mu(x_1)}{x_1}+\dfrac{\mu(x_2)}{x_2}+\dfrac{\mu(x_3)}{x_3}+\cdots+\dfrac{\mu(x_n)}{x_n}=\sum_{i=1}^n \dfrac{\mu(x_i)}{x_i}$$

اگر مجموعه $$U$$ نامتناهی باشد، مجموعه فازی را نامتناهی گویند. در این حالت مجموعه فازی را به جای استفاده از علامت $$\sum$$ با $$\int$$ نشان می‌دهند. برای مثال اگر $$x$$ در فاصله ۰ تا ۲ باشد، آنگاه مجموعه فازی $$A$$ را برحسب تابع عضویت $$\mu(x)$$ به صورت زیر نشان می‌دهند.

$$\large  A = \int_x \dfrac{\mu_A(x)}{x}$$

همانطور که می‌بینید در اینجا منظور از $$\int$$ «انتگرال» نیست زیرا اثری از $$dx$$ دیده نمی‌شود.

معمولا برای نمایش مجموعه‌های فازی، از نموداری در مختصات دکارتی استفاده می‌کنند. محور افقی در این نمودار، مقدارهای مربوط به مجموعه $$U$$‌ و محور عمودی نیز درجه عضویت برای اعضای مجموعه را نشان می‌دهد. فرض کنید که می‌خواهیم مجموعه‌ای از طول قد افراد بالای ۱۸۰ و کمتر از آن بسازیم. نمودار زیر تفاوت بین این مجموعه در حالت فازی و عادی را نشان می‌دهد.

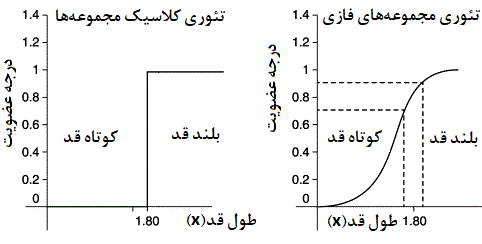
مجموعه‌ فازی و چند تعریف

فرض کنید $$A=(U,\mu_A)$$ و $$B=(U,\mu_B)$$ دو مجموعه فازی باشند. آنگاه روابط زیر برقرار است.

• اگر درجه عضویت تمام اعضای $$U$$ برای مجموعه فازی $$A$$ برابر با صفر باشد، مجموعه $$A$$ را تهی گویند. البته عکس این رابطه نیز صحیح است. یعنی اگر مجموعه فازی $$A$$ تهی باشد، درجه عضویت همه اعضای $$U$$ در آن برابر با صفر است. به بیان ریاضی خواهیم داشت: $$\forall x\in U:\mu _{A}(x)=0 \; \iff A=\emptyset$$

فیلم آموزش مکان یابی در سیستم اطلاعات جغرافیایی GIS با عملگرهای فازی در فرادرس

کلیک کنید

برای مثال اگر مجموعه $$A$$ به صورت زیر باشد، آنگاه تهی خواهد بود:

$$\large \{\frac{0}{x_1},\frac{0}{x_2},\cdots,\frac{0}{x_n}\}$$

• دو مجموعه $$A$$ و $$B$$ را برابر گویند اگر درجه‌های عضویت آن یکسان باشد. به بیان ریاضی خواهیم داشت: $$\forall x\in U:\mu _{A}(x)=\mu _{B}(x) \iff A=B$$

• مجموعه فازی $$A$$ زیر مجموعه یا مشمول مجموعه فازی $$B$$ است ($$A \subseteq B$$) اگر درجه عضویت برای همه اعضای مجموعه فازی $$A$$ از $$B$$ کمتر یا مساوی باشد. این گزاره را به زبان ریاضی به صورت $$\forall x\in U:\mu _{A}(x)\leq \mu _{B}(x) \iff A \subset B$$ می‌نویسیم.
• اگر عضوی از مجموعه فازی $$A$$ مثل $$x$$ وجود داشته باشد که $$\mu(x)=0.5$$ آنگاه $$x$$ را «نقطه گذر» (Crossover) می‌نامند.
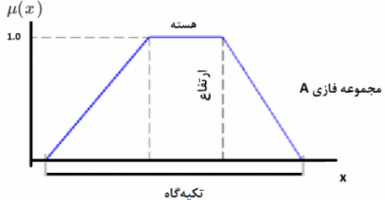
• مجموعه اعضای $$U$$ که برای آن‌ها مقدار درجه عضویت در مجموعه فازی A بزرگتر از صفر باشد، تکیه‌گاه (Support) مجموعه $$A$$ نامیده می‌شود. به این ترتیب $$S(A)=\{x \in U; \mu_A(x)>0\}$$
• $$\alpha$$-برش مجموعه $$A$$، که خود یک مجموعه فازی است، شامل اعضایی از مجموعه فازی $$A$$ با درجه عضویت بزرگتر از $$\alpha$$ خواهد بود. این مجموعه را به صورت $$A^{>\alpha}$$ نشان می‌دهند. تعریف ریاضی این مجموعه به صورت زیر نوشته می‌شود.

$$\large A^{>\alpha}=\{x \in A, \mu_A \geq \alpha \}, \;\; 0\leq \alpha \leq 1$$

نکته: اگر در تعریف $$\alpha$$-برش، از علامت < (بزرگتر اکید) استفاده کنیم، مجموعه حاصل را مجموعه، «$$\alpha$$-برش قوی» (Strong $$\alpha$$-cut) می‌گویند. با این بیان می‌توان گفت، تکیه‌گاه مجموعه فازی $$A$$، یک $$\alpha$$-برش قوی به ازاء $$\alpha=0$$ است. پس می‌توان نوشت: $$S(A)=Support(A)=A^{>0}=\{x\in U\mid \mu_A(x)>0\}$$.

• منظور از هسته (Kernel) یا (Core) مجموعه فازی $$A$$، زیر مجموعه‌ای از آن است که اعضای آن دارای درجه عضویت ۱ هستند، به این معنی که هسته مجموعه فازی A همان $$\alpha$$-برش مجموعه A به ازای $$\alpha=1$$ است. بیان ریاضی این گزاره به صورت $$kernel(A)=\{x \in U, \mid \mu_A(x) =1\}$$ نوشته می‌شود.
• ارتفاع (Height) مجموعه فازی $$A$$ را سوپریمم (کوچکترین کران بالا) برای درجه عضویت مجموعه $$A$$ می‌نامیم. به این ترتیب خواهیم داشت: $$Hgt(A)=sup\{\mu _{A}(x)\mid x\in {U}\}=sup_{x\in U}(\mu _{A}(x))$$
• براساس مفهوم ارتفاع، یک مجموعه فازی را نرمال می‌نامند، اگر ارتفاع آن برابر با ۱ باشد. بنابراین مجموعه $$A$$ نرمال است، اگر $$Hgt(A)=1$$.

نکته: اگر حداکثر درجه عضویت (ماکزیمم) یک مجموعه فازی غیر نرمال (زیر نرمال) یعنی $$\max{\big{(}\mu(x_i)\big{)}}$$

$$\large \mu(x_i)'=\dfrac{\mu(x_i)}{\max_{i}(\mu(x_i))}$$

• عدد اصلی یک مجموعه فازی مجموع درجه‌های عضویت آن مجموعه است. به این ترتیب برای مجموعه فازی A عدد اصلی که به صورت $$|A|$$ نشان داده می‌شود به صورت $$|A|=\sum_{x\in U} \mu_A(x)$$ محاسبه می‌شود.
• عدد اصلی نسبی برای یک مجموعه فازی نیز از تقسیم عدد اصلی بر تعداد اعضای مجموعه U ساخته می‌شود. پس اگر عدد اصلی نسبی را به صورت $$||A||$$ نشان دهیم خواهیم داشت: $$||A||=\frac{|A|}{|U|}$$. در اینجا منظور از $$|U|$$، تعداد اعضای مجموعه $$U$$ است.

مثال ۱

فرض کنید که مجموعه $$U$$, $$A$$ و $$B$$ به صورت زیر نوشته شده باشند.

$$\large U=\{x_1,x_2,x_3,x_4,x_5\} ,\\ \large A=\{\frac{0.1}{x_1},\frac{0.5}{x_2}, \frac{0.6}{x_3},\frac{0.9}{x_4}\}, \\ \large B=\{\frac{0.2}{x_1},\frac{0.5}{x_2},\frac{0.8}{x_3},\frac{1}{x_4},\frac{1}{x_5}\}$$

آنگاه، مشخص است که $$A\subset B$$ و تکیه‌گاه برای $$A$$ نیز به صورت $$S(A)=\{x_1,x_2,x_3,x_4\}$$ است. همچنین $$\alpha$$-برش مجموعه $$A$$ به ازای $$\alpha=0.5$$ برابر است با $$\{\frac{0.5}{x_2},\frac{0.6}{x_3},\frac{0.9}{x_4}\}$$. برهمین اساس، هسته برای مجموعه فازی $$B$$ برابر است با $$Core(B)=\{x_4,x_5\}$$. مشخص است که در مجموعه $$A$$ عضو $$x_2$$ نقطه گذر محسوب می‌شود.

نکته: بدیهی است که مجموعه‌های فازی $$\alpha$$-برش از مجموعه فازی $$A$$ همگی زیرمجموعه‌های $$A$$ محسوب می‌شوند.

رابطه مجموعه‌های فازی با یکدیگر

همانطور که در نظریه کلاسیک، «اشتراک» (Intersection)، «اجتماع» (Union) و همچنین «متمم» (Complement) دو مجموعه‌ها را معرفی کردیم، برای مجموعه‌های فازی نیز این مفاهیم تعریف شده و به کار می‌روند. در ادامه به بررسی این روابط بین مجموعه‌های فازی می‌پردازیم. در این قسمت فرض کنید که $$A=(U,\mu_A)$$ و $$B=(U,\mu_B)$$ دو مجموعه فازی باشند.

فیلم آموزش کاربرد فازی در سیستم های قدرت در فرادرس

کلیک کنید

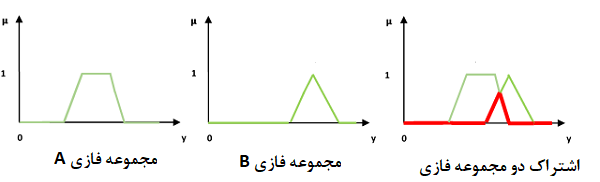
اشتراک دو مجموعه فازی

منظور از اشتراک دو مجموعه $$A$$ و $$B$$، مجموعه‌ای فازی از اعضای دو مجموعه است که درجه عضویت برای هر یک از اعضای آن حداقل درجه عضویتی است که در بین دو مجموعه $$A$$ و $$B$$ دارند. به این ترتیب خواهیم داشت:

$$\large \forall x\in {U}:\mu _{A\cap {B}}(x)=\min(\mu _{A}(x),\mu _{B}(x))$$

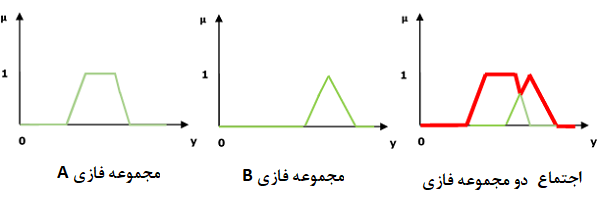
اجتماع دو مجموعه فازی

منظور از اجتماع دو مجموعه فازی $$A$$ و $$B$$، مجموعه‌ای فازی از اعضای دو مجموعه است که درجه عضویت برای هر یک از اعضای آن حداکثر درجه عضویتی است که در بین دو مجموعه $$A$$ و $$B$$ دارند. به این ترتیب خواهیم داشت:

$$\large \forall x\in {U}:\mu _{A\cup {B}}(x)=\max (\mu _{A}(x),\mu _{B}(x))$$

متمم مجموعه فازی

منظور از متمم مجموعه فازی $$A$$، باز هم یک مجموعه‌ای فازی مثل $$A'$$ است که تابع عضویت برای اعضای آن به صورت زیر نوشته می‌شود.

$$\large \forall x\in {U}:\mu _{A'}(x)=1-\mu _{A}(x)$$

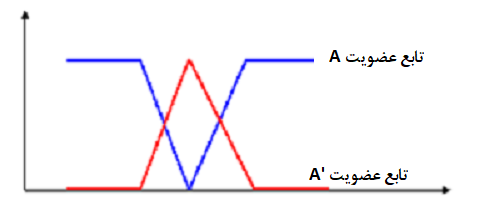
نکته: باید توجه داشت که برای محاسبه اشتراک، اجتماع دو مجموعه فازی $$A$$ و $$B$$، مجموعه $$U$$ باید یکسان باشد. به این ترتیب امکان مقایسه درجه‌های عضویت وجود داشته و می‌توان اشتراک و اجتماع را محاسبه کرد. در بیشتر موارد مجموعه $$U$$ را اعداد حقیقی در نظر می‌گیرند.

مثال ۲

فرض کنید که مجموعه‌های فازی $$A$$ و $$B$$ مربوط به مثال ۱ را در اختیار داریم. بنابر تعریف‌های گفته شده برای اشتراک، اجتماع و متمم مجموعه‌های فازی خواهیم داشت:

$$\large A\cap B = \dfrac{0.1}{x_1}+\dfrac{0.5}{x_2}+\dfrac{0.6}{x_3}+\dfrac{0.9}{x_4}+\dfrac{0}{x_5}$$

$$\large A\cup B = \dfrac{0.2}{x_1}+\dfrac{0.5}{x_2}+\dfrac{0.8}{x_3}+\dfrac{1}{x_4}+\dfrac{1}{x_5}$$

نکته: در این مثال دیده می‌شود که اشتراک دو مجموعه فازی، زیرمجموعه اجتماع آن دو مجموعه محسوب می‌شود، زیرا اعضای مجموعه اشتراک دارای درجه عضویت کمتری نسبت به مجموعه اجتماع هستند. می‌توان به صورت کلی نیز این قانون را بیان کرد که اشتراک دو مجموعه فازی زیر مجموعه اجتماع آن‌ها است. این وضعیت، به عنوان یک قضیه در نظریه مجموعه‌های کلاسیک نیز وجود دارد.

متمم مجموعه A و B‌ به ترتیب برابر هستند با:

$$\large A'=\dfrac{1-0.1}{x_1}+\dfrac{1-0.5}{x_2}+\dfrac{1-0.6}{x_3}+\dfrac{1-0.9}{x_4}+\dfrac{1-0}{x_5}=\\ \large \dfrac{0.9}{x_1}+\dfrac{0.5}{x_2}+\dfrac{0.4}{x_3}+\dfrac{0.1}{x_4}+\dfrac{1}{x_5}$$

$$\large B'=\dfrac{1-0.2}{x_1}+\dfrac{1-0.5}{x_2}+\dfrac{1-0.8}{x_3}+\dfrac{1-1}{x_4}+\dfrac{1-1}{x_5}=\\ \large \dfrac{0.8}{x_1}+\dfrac{0.5}{x_2}+\dfrac{0.2}{x_3}+\dfrac{0}{x_4}+\dfrac{0}{x_5}$$

همانطور که می‌بینید اشتراک مجموعه فازی $$A$$ با متممش یعنی $$A'$$ برخلاف تئوری کلاسیک مجموعه‌ها $$\emptyset$$ نیست. زیرا برای مثال

$$\large A \cap A'= \dfrac{0.1}{x_1}+\dfrac{0.5}{x_2}+\dfrac{0.4}{x_3}+\dfrac{0.1}{x_4}+\dfrac{1}{x_5}$$

و همچنین اجتماع مجموعه $$A$$ با متممش نیز مجموعه مرجع یعنی U را نمی‌سازد.

$$\large A \cup A'= \dfrac{0.9}{x_1}+\dfrac{0.5}{x_2}+\dfrac{0.6}{x_3}+\dfrac{0.9}{x_4}+\dfrac{1}{x_5}$$

نکته: همانطور که به یاد دارید اجتماع و اشتراک مجموعه‌ها در نظریه کلاسیک قابلیت جابجایی دارد. در اینجا نیز با توجه به رابطه‌ای که برای اشتراک و اجتماع دو مجموعه فازی بیان شد، می‌توان خاصیت جابجایی را برای این عملگرها روی مجموعه‌های فازی نیز اثبات کرد. همچنین مشخص است که اگر از مجموعه فازی $$A$$ دوبار متمم گرفته شود با مجموعه فازی $$A$$ برابر خواهد بود، یعنی $$(A')' = A$$.

دو مجموعه فازی جدا از هم (Disjoint)

اگر دو مجموعه فازی دارای تکیه‌گاه‌های متفاوت باشند، آنگاه «مجزا» (Disjoint) هستند. به این ترتیب می‌توان رابطه زیر را بین دو مجموعه فازی جدا از هم مشاهده کرد.

$$\large \forall x\in {U}:min(\mu _{A}(x),\mu _{B}(x))=0 \iff S(A) \neq S(B)$$

انواع مجموعه‌های فازی

براساس مجموعه مقدارها و شکل نمودار عضویت مجموعه‌های فازی آن را به چند دسته طبقه‌بندی می‌کنند. برای مثال اگر تابع درجه عضویت برای مجموعه فازی $$A$$ به شکل یک مثلث ترسیم شود، آن مجموعه را «مجموعه فازی مثلثی» (Triangle Fuzzy Set) می‌نامند.

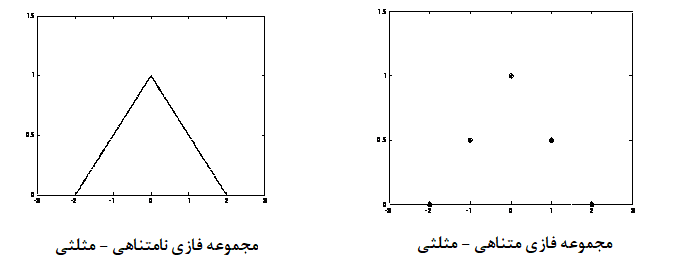
همانطور که می‌بینید، در تصویر سمت راست، فقط برای تعداد محدودی از نقاط اعداد حقیقی در محور افقی تابع عضویت مخالف صفر است. در نتیجه تکیه‌گاه این مجموعه متناهی است. از آنجایی که شکل این تابع به صورت مثلث ظاهر شده آن را مجموعه فازی متناهی مثلثی می‌نامند. برای این حالت می‌توان مجموعه فازی A را به صورت زیر نوشت:

$$\large A=\dfrac{\mu(x_1)}{x_1}+\dfrac{\mu(x_2)}{x_2}+\dfrac{\mu(x_3)}{x_3}+\dfrac{\mu(x_4)}{x_4}+\dfrac{\mu(x_5)}{x_5}=\sum_{i=1}^5 \dfrac{\mu(x_i)}{x_i}$$

همچنین در سمت چپ برای محدود اعداد حقیقی در فاصله ۲- تا ۲ تابع عضویت مشخص شده که به صورت یک تابع پیوسته است. بنابراین تکیه‌گاه مجموعه فازی دارای نامتناهی عضو است. به همین علت مجموعه را فازی نامتناهی نامیده‌اند. به این ترتیب مجموعه فازی A را به صورت انتگرال زیر نشان می‌دهیم.

$$\large \int_{-2}^0 \dfrac{\frac{2+x}{x}}{x}+\int_0^2 \dfrac{\frac{2-x}{x}}{x}$$

مشخص است که تابع عضویت برای مقدارهای کمتر از ۰ دارای شیب مثبت و برابر 0.5 و برای مقدارهای بزرگتر از ۰ دارای شیب منفی و برابر 0.5- است. به همین علت خطوط مثلث با محور افقی زاویه ۴۵ درجه و 135 درجه می‌سازند.

همینطور توابع عضویت «ذوزنقه‌ای» (Trapezoid) و «نمایی» (Exponent) نیز برای مجموعه‌های فازی وجود دارد. تصویر زیر این گونه مجموعه‌ها را معرفی کرده‌ است.

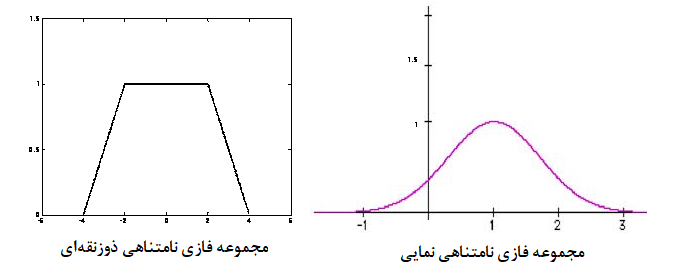
این مجموعه‌ها را می‌توان به صورت انتگرال نیز معرفی کرد. برای مثال در تصویر سمت چپ مجموعه فازی ذوزنقه‌ای را به صورت زیر نشان می‌دهیم.

$$\large A=\int_{-4}^{-2}\dfrac{\frac{4+x}{2}}{x}+\int_{-2}^2\dfrac{1}{x}+\int_2^4\dfrac{\frac{4-x}{2}}{x}$$

همچنین مجموعه فازی نمایی طبق رابطه زیر شناخته می‌شود.

$$\large A = \int_{x} e^{-0.5 (x-1)^2}$$

مشخص است که حداکثر این تابع در نقطه $$x=1$$ رخ داده و مقدار آن نیز برابر با ۱ است.

برای نمایش مجموعه‌های فازی بخصوص مجموعه‌های نامتناهی فازی، انتخاب تابع عضویت بسیار متنوع است و در هر شاخه ممکن است تابع خاصی را در نظر بگیرند.

در صورت علاقه‌مندی به مباحث مرتبط با مبانی و کاربردهای منطق فازی در حوزه‌های مختلف، آموز‌ش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه فیلم های آموزشی سیستم‌های فازی
• آموزش طراحی و تنظیم ضرایب کنترل کننده PID با منطق فازی
• محموعه آموزش‌های دروس مهندسی کنترل
• آموزش کنترل فعال سازه با رویکرد فازی با میراگر (ATMD)
• آموزش کاربرد فازی در سیستم‌های قدرت
• منطق دیجیتال — از صفر تا صد
• گزاره و سورهای منطقی — به زبان ساده

^^