لگاریتم طبیعی (ln) چیست؟ – به زبان ساده

در یکی از مطالب قبلی مجله فرادرس به بررسی تابع‌های نمایی پرداختیم و اینک نوبت به لگاریتم طبیعی رسیده است. با توجه به روش توصیف لگاریتم طبیعی در کتاب‌های درسی، می‌توان گفت که موارد طبیعی اندکی در مورد آن ارائه شده است، و اغلب به صورت معکوس ($$e^x$$) تعریف شده است که خود مفهوم پیچیده‌ای محسوب می‌شود. با این وجود، یک تعریف شهودی جذاب دیگر نیز برای لگاریتم طبیعی وجود دارد:

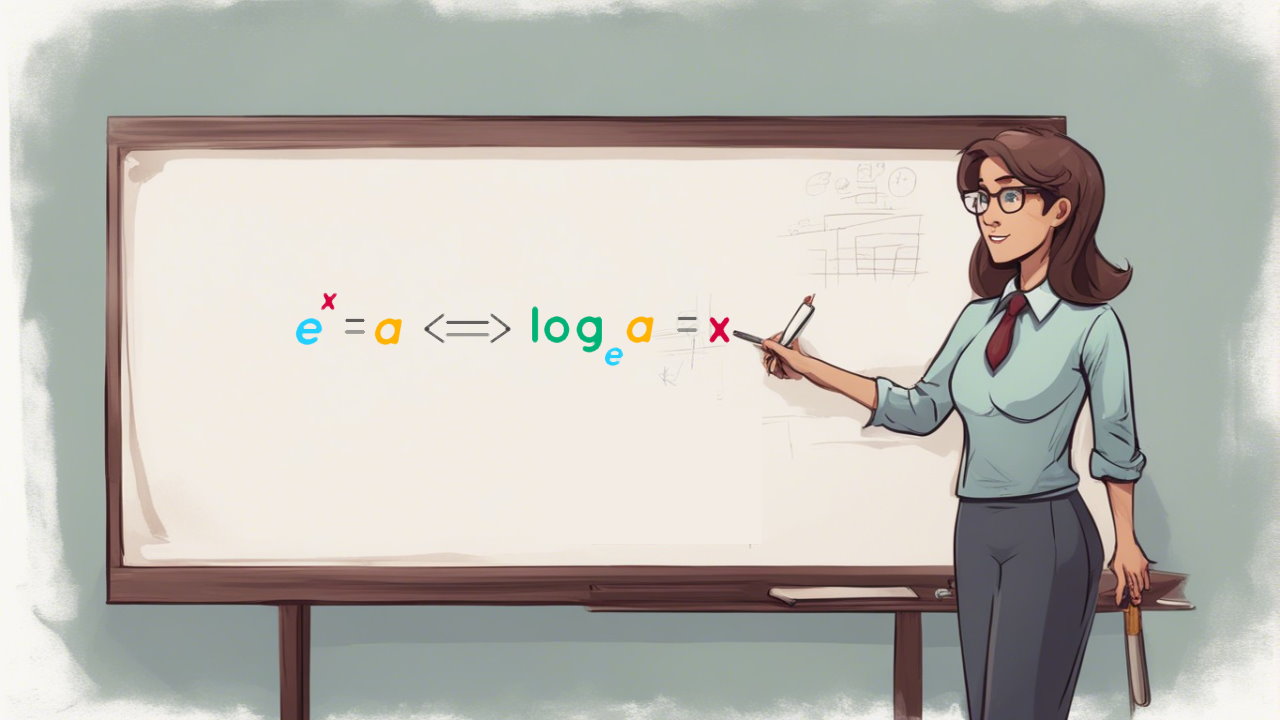
لگاریتم طبیعی زمان مورد نیاز برای رسیدن به حد معینی از رشد را ارائه می‌کند.

فرض کنید روی سهامی با نرخ بهره 100% سالانه سرمایه‌گذاری کرده باشید که به طور پیوسته‌‌ای رشد می‌کند. اگر بخواهید به رشد 10 برابری برسید با فرض ترکیب مداوم بهره روی سرمایه، کافی است زمانی برابر با (ln(10 یعنی 2.302 سال صبر کنید. اگر می‌خواهید در مورد این نرخ رشد بیشتر بدانید به مطلب عدد e مراجعه کنید.

e و لگاریتم طبیعی دو برادر دوقلو هستند:

• $$e^x$$ مقدار رشد پیوسته پس از مقدار معینی زمان است.
• لگاریتم طبیعی (ln) مقدار زمان مورد نیاز برای رسیدن به سطح خاصی از رشد پیوسته را نشان می‌دهد.

توضیح و تعریف ساده‌ای به نظر می‌رسد. زمانی که ریاضیدان‌ها تلاش می‌کنند توضیحات فنی پیچیده‌ای را ارائه کنند، سعی کنید مفاهیم ریاضی را به صورت شهودی درک کنید.

e به رشد مربوط است

عدد e در مورد رشد پیوسته است. همان طور که در مطلب قبلی دیدیم، $$e^x$$ امکان ادغام نرخ رشد و زمان را می‌دهد. 3 سال رشد با نرخ 100% همان نرخ رشد 1 ساله 300 درصدی است که به طور پیوسته ترکیب می‌شود.

می‌توان هر ترکیبی از نرخ رشد و زمان (50% برای 4 سال) را در نظر گرفت و نرخ رشد را برای سهولت به 100% تبدیل کرد (برای مثال نرخ رشد فوق به صورت 100% دو ساله خواهد بود). با تبدیل نرخ رشد به مقدار 100% کافی است، تنها عامل زمان را در نظر بگیریم:

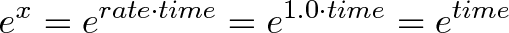
به طور شهودی $$e^x$$ به معانی زیر است:

• پس از x واحد زمان (و رشد پیوسته 100%) چه مقدار رشد به دست می‌آوریم.
• برای نمونه: پس از 3 دوره زمانی که $$e^3 = 20.08$$ برابر رشد به دست می‌آید.

$$e^x$$ عامل مقیاس‌بندی است که میزان رشدی را که پس از x دوره زمانی به دست می‌آوریم را نشان می‌دهد.

لگاریتم طبیعی در مورد زمان است

لگاریتم طبیعی معکوس e است که اصطلاحی جذاب برای یک متضاد به نظر می‌آید. منظور ما از جذاب نام لاتین logarithmus naturali است که به صورت ln اختصار می‌یابد.

اینک سؤال این است که معکوس یا متضاد در این زمینه به چه معنی است؟

• $$e^x$$ به ما کمک می‌کند با استفاده از زمان، رشد را محاسبه کنیم.
• (ln(x به ما کمک می‌کند با استفاده از رشد، زمانی که برای آن صرف شده است بیابیم.

برای نمونه:

• فرض کنید $$e^3$$ برابر با 20.08 باشد. پس از 3 واحد زمانی، به رشد 20.08 برابر آن چه که در آغاز داشتیم، می‌رسیم.
• (ln(20.08 در حدود 3 است. اگر بخواهیم رشدی به اندازه 20.08 برابر داشته باشیم، باید 3 واحد زمان (در این مورد نیز با فرض نرخ رشد پیوسته 100 درصدی) سپری شده باشد.

لگاریتم طبیعی زمان مورد نیاز به رسیدن به رشد مطلوب را مشخص می‌کند.

محاسبات لگاریتمی نرمال نیستند

اگر قبلاً لگاریتم‌ها را مطالعه کرده باشید، می‌دانید که موجودات عجیبی هستند. با استفاده از آن‌ها می‌توان ضرب را به جمع تبدیل کرد و همچنین تقسیم را به تفریق بدل ساخت.

برای مثال (ln(1 چیست؟ به طور شهودی سؤال این است که چه قدر باید صبر کنیم تا 1 برابر مقدار کنونی خود به دست آوریم؟

بدیهی است که پاسخ صفر است. ما هم‌اکنون نیز 1 برابر مقدار خود را داریم و زمانی برای رسیدن از 1 به 1 لازم نیست.

ln(1)=0

در مورد مقدار کسری چه می‌توان گفت، چه مقدار طول می‌کشد تا ½ مقدار کنونی خود را به دست آوریم؟ با فرض نرخ رشد پیوسته 100 درصدی می‌دانیم که( ln(2 مقدار زمان مورد نیاز برای رسیدن به دو برابر وضعیت کنونی است. اگر آن را معکوس کنیم (یعنی زمان را منفی در نظر بگیریم، باید نیمی از مقدار کنونی را به دست آوریم:

ln(0.5) =-ln(2) = -0.693

در واقع اگر 0.693 واحد زمانی به عقب بازگردیم (با فرض زمان منفی) نیمی از مقدار کنونی را خواهیم داشت. به طور کلی می‌توان با معکوس کردن کسر، مقدار منفی را به دست آورد: $$ln({1\over 3}) = – ln(3) = -1.09$$. این بدان معنی است که اگر 1.09 واحد زمانی به عقب بازگردیم، یک‌سوم آنچه اکنون داریم را به دست می‌آوریم.

اینک سؤال این است که در مورد لگاریتم طبیعی اعداد منفی چه می‌توان گفت؟ چه مقدار طول می‌کشد تا کولنی باکتری از 1 به 3- «رشد» کند؟

بدیهی است که ما نمی‌توانیم مقداری منفی از باکتری داشته باشیم. در کمترین مقدار، کلونی باکتری برابر با صفر خواهد بود؛ اما هیچ راهی برای این که مقداری منفی از یک چیز داشته باشیم وجود ندارد. لگاریتم منفی هیچ معنی ندارد.

 تعریف نشده است ln(عدد منفی)

منظور از تعریف نشده این است که هیچ مقداری از زمان وجود ندارد که شما منتظر بمانید تا یک مقدار منفی به دست آورید.

ضرب لگاریتمی می‌تواند جالب باشد

چه قدر طول می‌کشد تا مقدار کنونی خود را 4 برابر کنید. بدیهی است که باید از (ln(4 استفاده کنیم. اما این مثال ساده‌ای است و از این رو در ادامه وضعیت متفاوتی را بررسی می‌کنیم.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

می‌توان رشد 4 برابری را معادل دو بار رشد دو برابری در نظر گرفت. یعنی دو بار (ln(2 زمان را در نظر می‌گیریم.

زمان مورد نیاز برای رشد 4 برابر = (ln(4، یعنی دو برابر زمان مورد نیاز برای رشد دو برابری به صورت:

ln(2) + ln(2)

در واقع هر نرخ رشدی را می‌توان به صورت مضربی از رشد دو برابری یا مضارب دیگر تبدیل کرد. برای مثال رشد 20 برابری معادل 10 بار رشد دو برابری یا 4 بار رشد 5 برابری یا 3 بار رشد 6.666 برابری است. در این صورت الگوی زیر به دست می‌آید:

Ln(a×b) = ln(a) + ln(b)

لگاریتم a بار رشد b برابری برابر است با (log(a) + log(b. این رابطه در صورتی معنی می‌یابد که برحسب زمان مورد نیاز برای رشد فکر کنید.

اگر بخواهیم یک رشد 30 برابری داشته باشیم، هم می‌توانیم (ln(30 منتظر بمانیم و هم این که به مدت (ln(3 و سپس (ln(10 منتظر بمانیم. تأثیر خالص یکسان است و از این رو زمان مورد نیاز هم باید یکسان باشد و هست.

در مورد تقسیم نیز چنین است: $$ln({5\over 3})$$ یعنی چه قدر طول می‌کشد تا 5 برابر رشد کنیم و سپس $${1\over 3}$$ آن را محاسبه می‌کنیم.

می‌دانیم که زمان مورد نیاز برای رشد 5 برابری به صورت (ln(5 است. رشد $${5\over 3}$$ برابر با $$-ln({ 3})$$است و از این رو:

$$ln({a \over b}) = ln(a) – ln(b)$$

اینک قدرت محاسبات لگاریتمی خودش را نشان می‌دهد، به طوری که ضرب رشد به جمع زمان تبدیل می‌شود و تقسیم رشد به تفریق زمان. کافی است فرمول‌ها را صرفاً حفظ نکنید؛ بلکه درک کنید.

استفاده از لگاریتم طبیعی در هر نرخ رشد

مطمئناً تا کنون از خود پرسیده‌اید که همه این محاسبات در نرخ رشد 100% هستند، اما در مورد نرخ‌های رشد دیگر چه می‌توان گفت؟

در این مورد هیچ مانعی وجود ندارد. زمانی که ما از لگاریتم طبیعی کمک می‌گیریم در واقع ترکیبی از نرخ رشد و زمان است یعنی x در معادله $$e^x$$. ما آن را صرفاً به خاطر سادگی محاسبات 100% فرض کرده‌ایم؛ اما می‌توانیم از هر عدد دیگری نیز استفاده کنیم.

فرض کنید می‌خواهیم یک رشد 30 برابری داشته باشیم. با محاسبه (ln(30 عدد 3.4 را به دست می‌آوریم. این بدان معنی است که:

• $$e^x$$ =رشد
• $$e^{3.4} = 30$$

و به طور شهودی این معادله به این معنی است که «بازدهی 100% برای 3.4 سال معادل رشد 30 برابری است.» می‌توان معادله را به صورت زیر در نظر گرفت:

در واقع می‌توانیم نرخ و زمان را تا زمانی که مقدار نرخ×زمان برابر با 3.4 باشد تغییر دهیم. برای نمونه فرض کنید می‌خواهیم رشد 30 برابری داشته باشیم. در بازدهی 5% چه قدر باید صبر کنیم؟

ln(30) = 3.4

نرخ × زمان = 3.4

.05 ×زمان = 3.4

زمان = 3.4 /.05 = 68 سال

به طور شهودی می‌دانیم که ln(30) = 3.4 است و از این رو نرخ رشد 100 درصدی، 3.4 سال طول می‌کشد. اگر نرخ رشد را دو برابر کنیم، مقدار زمان نصف به دست می‌آید:

• 100% برای 3.4 سال = 1.0 × 3.4 = 3.4
• 200% برای 1.7 سال = 2.0 × 1.07 = 3.4 (رشد 200% باعث نصف شدن زمان می‌شود)
• 50% برای 6.8 سال = 0.5 × 6.8 = 3.4 (رشد 50 درصدی به معنی دو برابر شدن زمان است)
• 5% برای 8 سال = 0.05 × 68 = 3.4 (5 درصد رشد به معنی 20 برابر شدن زمان است)

لگاریتم طبیعی را می‌توان تا زمانی که محصول نهایی یکسان باشد، با هر نرخ بهره و هر زمانی استفاده کرد. می‌توانید متغیرها را به هر ترتیب که دوست دارید تغییر دهید.

مثال جالب: قاعده 72

قاعده 72 یک میانبر ذهنی ریاضی برای تخمین زمان مورد نیاز برای دو برابر کردن پول است. در ادامه این قاعده را بررسی کرده و سعی می‌کنیم آن را به طور شهودی درک کنیم.

با نرخ رشد 100% که به طور سالانه ترکیب می‌شود، چه مقدار طول می‌کشد تا پول خود را دو برابر کنید؟

ما تا کنون از لگاریتم طبیعی برای نرخ رشد پیوسته استفاده کرده‌ایم؛ اما اینک در مورد بهره سالانه سؤال شده است. بدین ترتیب فرمول تغییر می‌یابد؛ اما در مورد نرخ‌های بهره معقولی مانند 5، 6 و یا حتی 15 درصد تفاوت چندانی بین ترکیب سالانه و یا ترکیب کاملاً پیوسته وجود ندارد. بنابراین فرمول اولیه همچنان به طور نسبی کار می‌کند و می‌توان نرخ بهره کاملاً مرکب را به دست آورید.

اینک سؤال این است که با نرخ بهره 100% چه مقدار طول می‌کشد تا موجودی خود را دو برابر کنیم؟ می‌دانیم که ln(2) = 0.693 است. یعنی 0.693 واحد زمانی (در این مثال سال) طول می‌کشد تا پول خود را با نرخ بهره مرکب 100 درصدی دو برابر کنیم.

حال اگر نرخ بهره 100 درصد نباشد و 5 یا 10 درصد باشد چطور؟

پاسخ ساده است. تا زمانی که نرخ * زمان = 0.693 باشد، می‌توانیم به صورت زیر دو برابر پول خود را حساب کنیم:

• نرخ × زمان = 0.693
• زمان = نرخ÷0.693

بنابراین اگر ما تنها یک نرخ رشد 10% داشته باشیم، می‌توانیم در طی حاصل تقسیم 0.1÷0.693 یا 6.93 سال آن را دو برابر کنیم.

برای ساده‌تر کردن موضوع، حالت ضرب در 100 یعنی درصد را فرض کنید، بدین ترتیب می‌توانیم به جای 0.1 مقدار 10 را استفاده کنیم:

زمان مورد نیاز برای رشد دو برابری = (نرخ ÷ 693) که نرخ رشد به صورت درصد به دست می‌آید.

اینک زمان مورد نیاز برای دو برابر کردن موجودی با نرخ 5% برابر با 5÷69.3 یا 13.86 سال خواهد بود. با این حال 69.3 عدد چندان تقسیم‌پذیری محسوب نمی‌شود. می‌توانیم همسایه نزدیک‌تر آن 72 را در نظر بگیریم که می تواند بر 2، 3، 4، 6، 8 و اعداد زیاد دیگری تقسیم شود.

زمان مورد نیاز برای رشد دو برابری = نرخ÷72

که به قاعده 72 مشهور است.

اگر بخواهید زمان مورد نیاز برای رشد سه برابری را حساب کنید، می‌توانید از ln(3) ~ 109.8 استفاده کنید:

زمان مورد نیاز برای رشد سه برابری = نرخ÷110

که قاعده سرانگشتی مفید دیگری محسوب می‌شود. قاعده 72 برای نرخ‌های بهره، رشد جمعیت، کِشت باکتری و هر چیزی که با رشد نمایی سر و کار دارد، مفید است.

یک سؤال ساده

(ln(e چه مقدار است؟

به بیان خشک ریاضی می‌توان گفت از آنجا که این دو تابع معکوس هم هستند، بدیهی است که ln(e) = 1 خواهد بود.

اما به طور شهودی می‌توان تصور کرد که (ln(e مقدار زمان مورد نیاز برای رسیدن به e واحد از رشد (حدود 2.718) است؛ اما از طرف دیگر می‌دانیم که e مقدار رشد به دست آمده پس از 1 واحد زمانی است. بنابراین ln(e)=1.

سخن پایانی

امیدواریم با مطالعه این نوشته، لگاریتم طبیعی معنای عمیق‌تری در ذهن شما یافته باشد. در واقع لگاریتم طبیعی در مورد زمان مورد نیاز برای حد مشخصی از رشد نمایی صحبت می‌کند. دلیل این که آن را طبیعی می‌نامیم این است که e ثابت کلی رشد است و از این رو می‌توان آن را روشی کلی برای محاسبه مدت زمان مورد نیاز برای رشد تصور کرد.

هر زمان که (ln(x را می‌بینید بدانید که در مورد «زمان مورد نیاز برای رشد به x صحبت می‌شود».