فاصله اطمینان (Confidence Interval) – به زبان ساده

محققان و تحلیلگران، اغلب در مباحث آمار و داده‌کاوی، از عبارت «فاصله اطمینان» (Confidence Interval) استفاده می‌کنند تا نشان دهند که تقریبا مطمئن هستند یک فاصله یا محدوده‌ای عددی، شامل پارامتر مورد جامعه است. پس می‌توان فاصله اطمینان را نوعی برآورد فاصله‌ای در نظر گرفت. این پارامتر را اغلب با CI نشان می‌دهند.

فاصله اطمینان با مفهوم مربوط به «سطح اطمینان» (Confidence Level) ارتباط نزدیکی دارد. منظور از سطح اطمینان، تعیین میزان شک یا یقینی است که نسبت به دربرگیری پارامتر توسط CI، داریم.

در حقیقت این محدوده، توسط یک نمونه تصادفی محاسبه می‌شود، در نتیجه می‌توان CI را یک محدوده تصادفی در نظر داشت. با انتخاب نمونه دیگر، محاسبات برای این محدوده تغییر کرده و یک فاصله اطمینان متفاوت بدست خواهد آمد. به همین علت با سطح اطمینان مشخص، خانواده‌ای از فاصله‌های اطمینان با توجه نمونه‌های مختلف تولید می‌شود.

به این ترتیب می‌توان گفت سطح اطمینان، فراوانی نسبی، فاصله‌‌های اطمینانی است که شامل پارامتر مجهول جامعه هستند. به بیان دیگر، اگر n فاصله اطمینان با سطح اطمینان ثابت ایجاد کنیم، نسبت آن‌هایی که شامل پارامتر هستند به کل فاصله‌ها، برابر با همان سطح اطمینان خواهد بود. هدف در محاسبه CI، بدست آوردن حدودی برای پارامتر است که در سطح اطمینان تعیین شده، شامل پارامتر باشد.

برای درک بهتر این نوشتار بهتر است که مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را که در مورد تابع احتمال و ویژگی‌هایی متغیر تصادفی است، قبلا مطالعه کرده باشید. همچنین با توجه به قرابت موضوع فاصله اطمینان با آزمون فرض آماری و برآورد فاصله‌ای، خواندن مطلب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات خالی از لطف نیست.

فاصله اطمینان

فرض کنید قد ۴۰ نفر  که به طور تصادفی انتخاب شده‌اند، اندازه‌گیری شده است. میانگین قد این افراد برابر است با ۱۷۵ سانتی‌متر. از طرفی می‌دانیم که انحراف معیار قد در جامعه آماری ما برابر است با ۲۰ سانتی‌متر.

با توجه به این موضوع، فاصله اطمینان برای میانگین قد افراد جامعه با سطح اطمینان ۹۵ درصدی برابر است با

$$175 cm \pm 6.2 cm$$

فاصله اطمینان بیان می‌کند که اگر ۱۰۰ بار نمونه‌گیری تکرار شود و ۱۰۰ فاصله اطمینان ۹۵٪ تولید شود، 95 فاصله شامل پارامتر جامعه خواهند بود و فقط 5 تا از این فاصله‌ها شامل میانگین جامعه نمی‌شوند.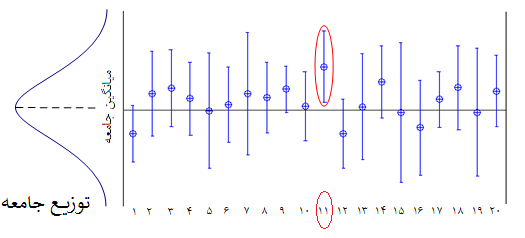

نکته: سطح اطمینان در اینجا برابر با ۹۵٪ است. پس ممکن است در ۵٪ مواقع به فاصله اطمینانی برخورد کنیم که دربرگیرنده پارامتر جامعه نباشد.تصویر بالا این امر را بهتر نشان می‌دهد.  همانطور که دیده می‌شود یکی از ۲۰ فاصله اطمینان شامل میانگین جامعه نیست. پس سطح اطمینان برای این فاصله ‌ها  95٪ یا میزان خطا برابر با 5٪ است.

متاسفانه پارامتری که قصد داریم برای آن یک فاصله اطمینان ایجاد کنیم،‌ نامعلوم است (اگر این پارامتر معلوم بود دیگر احتیاجی به فاصله اطمینان نداشتیم) در نتیجه هرگز نمی‌توانیم پی‌ببریم که فاصله اطمینان بدست آمده حتما شامل پارامتر اس یا خیر.

به توجه به این توضیحات مشخص است که برای ایجاد فاصله اطمینان، باید سطح اطمینان مشخص شده باشد. معمولا سطح اطمینان را با $$1-\alpha$$ نشان می‌دهند که در آن $$\alpha$$ همان احتمال خطای نوع اول در آزمون فرض آماری است.

پس به نظر می‌رسد هدف از ایجاد فاصله اطمینان، بدست آوردن فاصله‌ای تصادفی است که با احتمالی برابر با سطح اطمینان $$1-\alpha$$، شامل پارامتر باشد.

$$P(L(X)\leq\theta\leq U(X))=1-\alpha$$

در اینجا $$L(X)$$ و $$U(X)$$ حدود فاصله اطمینان هستند که برحسب نمونه تصادفی حاصل می‌شوند.

برای بدست آوردن CI باید علاوه بر اطلاع از سطح اطمینان، تابعی از نمونه تصادفی ایجاد کرد که بتوان برای آن احتمال را محاسبه نمود، بدون اینکه احتیاجی به دانستن پارامتر مجهول باشد. به چنین تابع، «کمیت محوری» (Pivotal Quantity) می‌گویند.

کمیت محوری

کمیت محوری، تابعی است از نمونه تصادفی و پارامترها، که توزیع آن به پارامتر یا پارامترهای مجهول بستگی ندارد. با توجه به این تعریف مشخص است که کمیت محوری، ماهیتی تصادفی دارد. یعنی با تغییر نمونه تصادفی، این کمیت نیز تغییر خواهد کرد. از طرفی این تابع دارای توزیع احتمالی است که به پارامتر مجهول بستگی ندارد، در نتیجه محاسبه تابع توزیع یا احتمال برای آن با مشکل مواجه نخواهد شد. معمولا کمیت محوری را با Q نشان می‌دهند.

اگر رابطه بالا را براساس کمیت محوری بازنویسی کنیم، خواهیم داشت:

$$P(a\leq Q \leq b)=1-\alpha$$

به این ترتیب اگر a و b به شکلی باشند که $$P(Q\leq a)=P(q\geq b)=\frac{\alpha}{2}$$ آنگاه فاصله اطمینان حاصل را با دم‌های برابر می‌نامند.

پس از پیدا کردن فاصله اطمینان برای کمیت محوری یعنی محاسبه کران‌های a و b، می‌توان برای پارامتر $$\theta$$ نیز کران‌های $$L(X)$$ و $$U(X)$$ را بدست آورد، زیرا در کمیت محوری از پارامتر نامعلوم $$\theta$$ استفاده شده است، بنابراین با یک تبدیل معکوس به راحتی کران‌های CI محاسبه می‌شوند.

مراحل ساخت فاصله اطمینان برای میانگین جامعه نرمال

فرض کنید $$X_1,X_2,\ldots , X_n$$ نمونه‌های تصادفی از متغیر تصادفی X باشند که دارای توزیع نرمال با میانگین $$\mu$$‌ و واریانس $$\sigma^2$$ است. یعنی $$X\sim N(\mu.\sigma^2)$$.

فیلم آموزش استنباط آماری پارامتری در Minitab (رایگان) در فرادرس

کلیک کنید

هدف در اینجا ساختن فاصله اطمینان برای میانگین جامعه است. از آنجایی که احتیاج به یک کمیت محوری داریم، بهتر است از برآورد نقطه‌ای میانگین جامعه استفاده کنیم. در جامعه نرمال، برآوردگر نقطه‌ای برای میانگین جامعه ($$\mu$$) می‌تواند $$\overline{X}$$ باشد. پس سعی داریم در اینجا به کمک برآوردگر نقطه‌ای برای میانگین جامعه، فاصله اطمینان را محاسبه کنیم.

با توجه به فرضیاتی که در این قسمت گفته شد، می‌دانیم توزیع $$\overline{X}$$ برابر است با

$$\overline{X}\sim N(\mu,\frac{\sigma^2}{n})$$

از طرفی می‌دانیم که $$\overline{X}-\mu$$‌ دارای توزیع نرمال با میانگین صفر است. پس داریم:

$$\overline{X}-\,u\sim N(0,\frac{\sigma^2}{n})$$

از این تابع، می‌توان برای تشکیل کمیت محوری استفاده کرد به شرط آن که واریانس جامعه معلوم باشد. در نتیجه باید با توجه به معلوم و نامعلوم بودن واریانس جامعه توزیع این تابع را مشخص کرده سپس به ساختن فاصله اطمینان بپردازیم. پس دو وضعیت را بررسی می‌کنیم : ۱- «واریانس جامعه معلوم« (Variance Known) باشد. ۲- «واریانس جامعه نامعلوم» (Variance Unknown) است.

فاصله اطمینان برای میانگین با فرض معلوم بودن واریانس

با توجه به فرضیات بالا، سعی داریم احتمال زیر را محاسبه می‌کنیم.

$$P(L(\overline{X})\leq\mu U(\overline{X}))=1-\alpha$$

می‌دانیم که

$$Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt n}}\sim N(0,1)$$

در نتیجه از Z به عنوان تابع محوری می‌توان استفاده کرد. بنابراین خواهیم داشت.

$$P(a\leq Z \leq b)=1-\alpha$$

همچنین اگر a را قرینه b در نظر بگیریم، می‌توانیم رابطه بالا را به صورت زیر بنویسیم.

$$P(-b\leq Z \leq b)=1-\alpha$$

از آنجایی که Z دارای توزیع نرمال استاندارد است، پس دارای توزیع متقارن بوده (فاصله اطمینان با دم‌های برابر) و طرف چپ تساوی را می‌توان با توجه به قوانین محاسبه برحسب تابع توزیع احتمال، به صورت زیر نوشت:

$$P(Z\leq b)-P(Z\leq -b)= \Phi(b)-\Phi(-b)$$

نکته: می‌دانیم که منظور از $$\Phi(b)$$‌ مقدار تابع توزیع احتمال تجمعی نرمال استاندارد در نقطه b است.

از طرفی می‌دانیم که $$\Phi(-b)=1-\Phi(b)$$ پس خواهیم داشت:

$$P(Z\leq b)-P(Z\leq -b)= \Phi(b)-(1-\Phi(b))=2\Phi(b)-1$$

پس رابطه بین $$\alpha$$ و $$\Phi(b)$$ به صورت زیر خواهد بود:

$$2\Phi(b)-1=1-\alpha\rightarrow 2(\Phi(b)-1)=\alpha\rightarrow \Phi(b)=1-\frac{\alpha}{2}$$

پس مقدار b برابر است با $$\Phi^{-1}(1-\frac{\alpha}{2})$$. حال رابطه اصلی را با توجه به مقدار b بازنویسی می‌کنیم.

$$P(-\Phi^{-1}(1-\frac{\alpha}{2}) \leq Z \leq \Phi^{-1}(1-\frac{\alpha}{2}))=1-\alpha$$

و سپس Z را جایگذاری کرده و فاصله اطمینان را بدست خواهیم آورد.

نکته: منظور از $$\Phi^{-1}(\alpha)$$ صدک $$\alpha$$ام توزیع نرمال استاندارد است.

$$P(-\Phi^{-1}(1-\frac{\alpha}{2}) \leq \frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt n}} \leq \Phi^{-1}(1-\frac{\alpha}{2}))=1-\alpha$$

پس

$$P(-\Phi^{-1}(1-\frac{\alpha}{2}){\frac{\sigma}{\sqrt n}} \leq \overline{X}-\mu \leq \Phi^{-1}(1-\frac{\alpha}{2}){\frac{\sigma}{\sqrt n}})=1-\alpha$$

در نتیجه خواهیم داشت:

$$P(\overline{X}-\Phi^{-1}(1-\frac{\alpha}{2}){\frac{\sigma}{\sqrt n}} \leq \mu \leq\overline{X}+ \Phi^{-1}(1-\frac{\alpha}{2}){\frac{\sigma}{\sqrt n}})=1-\alpha$$

معمولا مقدار $$\Phi^{-1}(1-\frac{\alpha}{2})$$ را با $$z_{(1-\frac{\alpha}{2})}$$ نشان می‌دهند که همان صدک $$1-\frac{\alpha}{2}$$ توزیع نرمال استاندارد است. با توجه به این فرم رابطه فاصله اطمینان به صورت زیر در خواهد آمد:

$$P(\overline{X}-z_{(1-\frac{\alpha}{2})}{\frac{\sigma}{\sqrt n}} \leq \mu \leq\overline{X}+ z_{(1-\frac{\alpha}{2})}{\frac{\sigma}{\sqrt n}})=1-\alpha$$

پس می‌توان گفت که فاصله زیر با احتمال $$1-\alpha$$ شامل میانگین جامعه خواهد بود.

$$(\overline{X}-z_{(1-\frac{\alpha}{2})}{\frac{\sigma}{\sqrt n}}\;\; ,\;\;\overline{X}+ z_{(1-\frac{\alpha}{2})}{\frac{\sigma}{\sqrt n}})$$

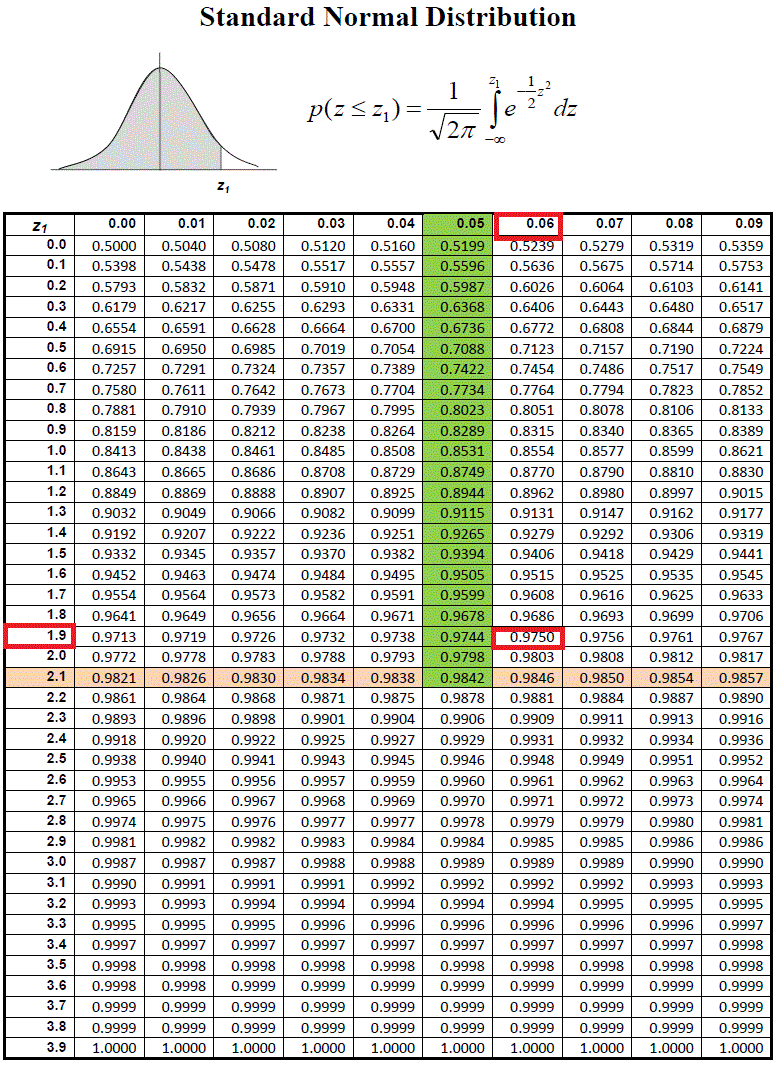
نکته: به کمک نرم‌افزارها و جداول آماری مربوط به توزیع نرمال استاندارد، می‌توان مقدار $$z_{(1-\frac{\alpha}{2})}$$ را براساس $$\alpha$$های مختلف پیدا کرد.

 معمولا دو کاربرد برای این جدول وجود دارد. برای آشنایی با نحوه استفاده از این جدول از مثال‌های زیر استفاده می‌کنیم.

مثال ۱

فرض کنید متغیر تصادفی X‌ دارای توزیع نرمال با میانگین ۵ و انحراف استاندارد 4 باشد. برای محاسبه احتمال $$P(X\leq 13.6)$$ به ترتیب زیر عمل می‌کنیم. از آنجایی که این جدول برای محاسبه احتمال متغیر تصادفی نرمال استاندارد قابل استفاده است، ابتدا باید متغیر تصادفی X را استاندارد کرده و به متغیر تصادفی Z تبدیل کنیم.

$$Z=\dfrac{X-5}{4}$$

محاسبه بالا با توجه به میانگین و انحراف استاندارد متغیر تصادفی X صورت گرفته است. حال احتمال مورد نظر باید برحسب Z بیان شود.

$$P(X\leq 13.6)=P(\dfrac{X-5}{4}\leq \dfrac{13.6-5}{4})=P(Z\leq 2.15)=0.9842$$

برای پیدا کردن این احتمال توسط جدول به ترتیب زیر عمل می‌کنیم. فرض کنید منظورمان پیدا کردن مقدار احتمال تا نقطه 2.15 از توزیع نرمال استاندارد است.

1. رقم یکان و اولین رقم اعشاری مقدار مورد نظر (2.1) را در ستون اول جدول پیدا می‌کنیم. حاصل را از عدد اولیه کم کرده و نتیجه تفاضل ($$2.15-2.1=0.05$$) را نیز در سطر اول جدول جستجو می‌کنیم. ممکن است این تفاضل برابر با صفر شود. در این حالت در ستون دوم (0.00) جدول جستجو را ادامه می‌دهیم.
2. محل تقاطع سطر (نارنجی) و ستون (سبز رنگ) حاصل از مرحله قبل را در جدول مشخص می‌کنیم. عدد نمایش داده شده، احتمال مورد نظر است. (0.9842)

نکته: با توجه به جدول مشخص است که احتمال فقط برای مقدارهای مثبت Z نوشته شده است. برای پیدا کردن احتمال در زمانی که مقدار z منفی است، از قاعده زیر استفاده کنید.

$$P(Z\leq z)=P(Z\geq -z)=1-P(Z\leq -z),\;\;\; z\leq 0$$

مثلا اگر می‌خواهید $$P(Z\leq -2.15)$$ را محاسبه کنید به صورت زیر عمل می‌کنیم:

$$P(Z\leq -2.15)=P(Z\geq -(-2.15))=P(Z\geq 2.15)=1-P(Z\leq 2.15)=1-0.9842=0.0158$$

مثال ۲

فرض کنید وزن یک نمونه ۴6 تایی از سیب‌های یک مزرعه اندازه‌گیری شده است. می‌دانیم که انحراف استاندارد وزن سیب‌ها برابر است با 6.2 گرم . اگر میانگین وزن این نمونه برابر با 86 گرم باشد، با سطح اطمینان 95٪،‌ برای میانگین وزن سیب‌های مزرعه، فاصله اطمینان به صورت زیر در خواهد آمد:

$$(\overline{X}-z_{(1-\frac{\alpha}{2})}{\frac{\sigma}{\sqrt n}}\;\; ,\;\;\overline{X}+ z_{(1-\frac{\alpha}{2})}{\frac{\sigma}{\sqrt n}})$$

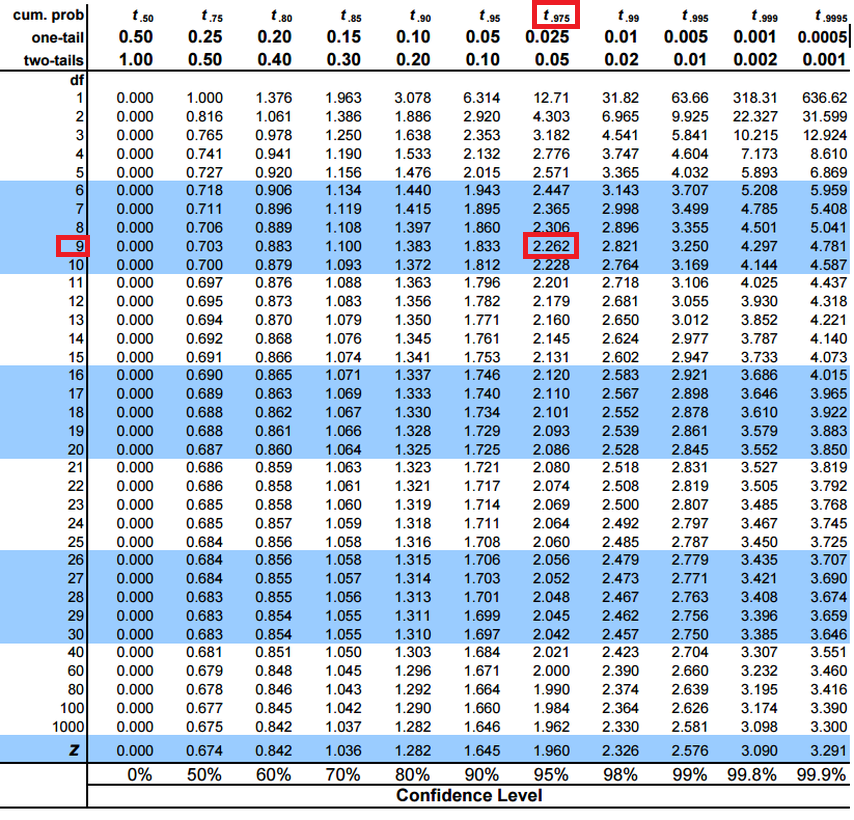
با توجه به اینکه سطح اطمینان برابر با 95٪ است، مشخص است که احتمال خطا برابر است با $$\alpha=0.05$$. یعنی داریم $$\frac{\alpha}{2}=0.025$$. به این ترتیب مقدار $$z_{1-0.025}= z_{0.975}=1.96$$ از روی جدول بالا (کادرهای قرمز رنگ) بدست می‌آید. پس خواهیم داشت:

$$(86-1.96 \frac{6.2}{\sqrt 46}\;\; ,\;\;86+1.96\frac{6.2}{\sqrt 46})$$

$$(84.21\;\; ,\;\;87.79)$$

پس می‌توان گفت که این فاصله، با احتمال 95٪ شامل میانگین وزن سیب‌های مزرعه خواهد بود.

نکته: برای محاسبه $$z_{0.975}$$ طبق «جدول احتمال تجمعی متغیر تصادفی نرمال استاندارد»، در داخل جدول مقدار 0.975 را پیدا می‌کنیم. مقدار سطر اول و ستون اول متناظر با این مقدار را از جدول با یکدیگر جمع می‌کنیم تا مقدار z مربوطه بدست آید که در اینجا مقدار سطر اول برابر با 0.06 و ستون اول 1.9 خواهد بود. جمع این دو مقدار یعنی 1.96، هزارک 975ام (صدک 97.5) یا همان $$z_{0.975}$$ را نشان می‌دهد.

فاصله اطمینان برای میانگین با فرض نامعلوم بودن واریانس

برای محاسبه فاصله اطمینان در این حالت نیز، از برآورد نقطه‌ای میانگین جامعه یعنی میانگین نمونه‌‌ای $$\overline{X}$$ استفاده می‌شود. ولی با توجه به اینکه واریانس (انحراف معیار) جامعه مشخص نیست از کمیت محوری قبلی نمی‌توان استفاده کرد، زیرا  توزیع آن مشخص نیست. در زمانی که حجم نمونه (n) کم باشد، برآورد واریانس جامعه، واریانس نمونه‌ای یعنی $$S^2$$ خواهد بود، پس می‌توانیم کمیت محوری را به صورت زیر معرفی کنیم:

$$\displaystyle T={\frac {{\bar {X}}-\mu }{S/{\sqrt {n}}}}$$

که در آن واریانس نمونه‌ای به صورت زیر محاسبه می‌شود:

$$\displaystyle S^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\bar {X}}\,)^{2}$$

به این ترتیب، می‌دانیم که T دارای توزیع t با n-1 درجه آزادی است. یعنی داریم $$T\sim t(n-1)$$. با توجه به این موضوع، T می‌تواند یک کمیت محوری باشد، پس می‌توانیم با انجام مراحلی که در قبل برای ایجاد فاصله اطمینان میانگین جامعه طی کردیم، CI را محاسبه کنیم. یعنی بنویسیم:

$$P(-b\leq T \leq b)=1-\alpha$$

با انجام محاسبات مربوطه، در نهایت به رابطه زیر خواهیم رسید:

$$P(\overline{X}-t_{(n-1,1-\frac{\alpha}{2})}{\frac{S}{\sqrt n}} \leq \mu \leq\overline{X}+ t_{(n-1,1-\frac{\alpha}{2})}{\frac{S}{\sqrt n}})=1-\alpha$$

پس در سطح اطمینان $$1-\alpha$$ محدوده زیر شامل میانگین جامعه خواهد بود.

$$(\overline{X}-t_{(n-1,1-\frac{\alpha}{2})}{\frac{S}{\sqrt n}} \;\;,\;\;\overline{X}+ t_{(n-1,1-\frac{\alpha}{2})}{\frac{S}{\sqrt n}})$$

مثال ۳

داده‌های زیر مربوط به میزان pH در 10 نمونه از آب معدنی یک شرکت است. فاصله اطمینان 95 و 99 درصدی برای میانگین pH تولیدات آب معدنی این شرکت به صورت زیر محاسبه می‌شود.

میانگین نمونه‌ای برابر خواهد بود با $$\overline{X}=6.52$$ و انحراف استاندارد نمونه‌ای نیز $$s=0.11$$.

اگر سطح اطمینان را 95٪ در نظر بگیریم، خواهیم داشت:

$$1-\alpha=0.95\rightarrow \alpha=0.05\rightarrow \frac{\alpha}{2}=0.025\rightarrow 1-\frac{\alpha}{2}=1-0.025=0.975$$

$$t_{10-1,1-\frac{0.5}{2}}=t_{9,0.975}=2.262$$

در نتیجه طبق رابطه فاصله اطمینان می‌توان نوشت:

$$(\overline{X}-t_{(n-1,1-\frac{\alpha}{2})}{\frac{S}{\sqrt n}} \;\;,\;\;\overline{X}+ t_{(n-1,1-\frac{\alpha}{2})}{\frac{S}{\sqrt n}})$$

پس

$$(6.52-2.262\frac{0.11}{\sqrt{10}}\;\;,\;\;6.52+2.62\frac{0.11}{\sqrt{10}})$$

در نتیجه فاصله اطمینان به صورت زیر خواهد بود:

$$(6.44,6.60)$$

نکته: برای محاسبه مقدار صدک‌های توزیع t می‌توان از نرم‌افزارهای محاسباتی یا جداول آماری توزیع t استفاده کرد. در زیر یک نمونه از این جدول دیده می‌شود. برای نحوه استفاده از این جدول، محاسبات مثال قبل را مورد بررسی قرار می‌دهیم. در مثال ۳ احتیاج به مقدار $$t_{9,0.975}$$ داریم. در سطر اول جدول مقدار t0.975 و در ستون اول نیز مقدار ۹ را پیدا می‌کنیم. تقاطع این سطر و ستون مقدار هزارک 975ام توزیع t با ۹ درجه آزادی است. البته در سطر آخر جدول نیز سطح اطمینان (0.95) برای CI مشخص شده که از آن هم برای تشکیل فاصله اطمینان و تعیین صدک یا هزارک توزیع t می‌توان استفاده کرد.

طول و دقت در فاصله اطمینان

طول این فاصله برابر است با 0.16. به این ترتیب مشخص است که انحراف این فاصله از میانگین جامعه برابر است با 0.16. از طرفی می‌توان دقت این فاصله اطمینان را با عکس طول آن متناسب دانسنت. در نتیجه دقت این فاصله برابر است با $$\frac{1}{0.16}=6.25$$.

حال با سطح اطمینان 99٪ فاصله اطمینان را محاسبه می‌کنیم. کافی است که در محاسبات، $$t_{n-1,1-\frac{\alpha}{2}}$$ را بدست آورده و جایگذاری را انجام دهیم.

$$1-\alpha=0.99\rightarrow \alpha=0.01\rightarrow \frac{\alpha}{2}=0.005\rightarrow 1-\frac{\alpha}{2}=1-0.005=0.995$$

پس

$$62.52-3.250\frac{0.11}{\sqrt{10}}\;\;,\;\;6.52+3.250\frac{0.11}{\sqrt{10}})$$

در نتیجه فاصله اطمینان به صورت زیر خواهد بود:

$$(6.41,6.63)$$

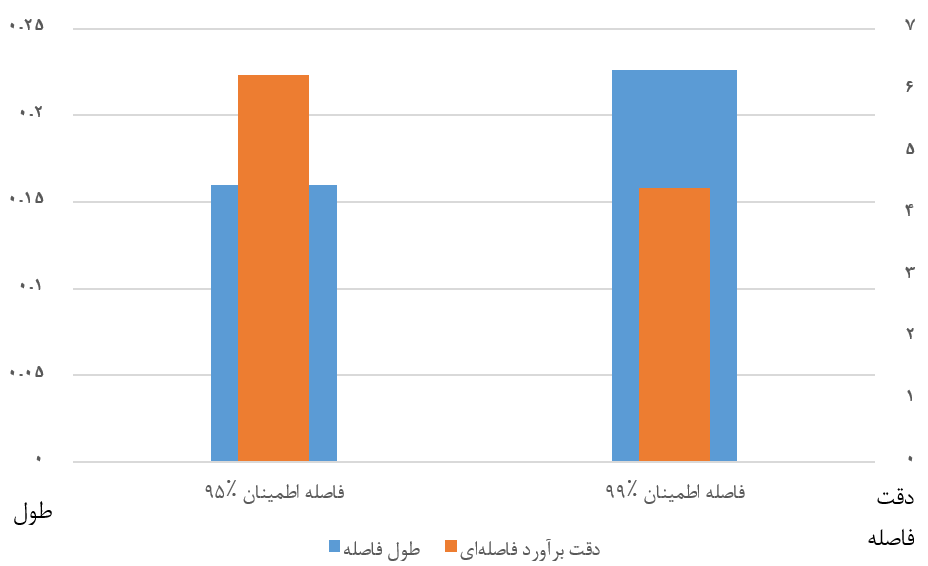
طول این فاصله اطمینان نیز برابر است با 0.23، در نتیجه دقت آن نیز برابر خواهد بود با 4.42، در نتیجه با مقایسه فاصله اطمینان 95٪ با فاصله اطمینان 99٪ مشاهده می‌شود که طول فاصله اطمینان اولی کمتر از دومی است یا به عبارتی می‌توان گفت دقت فاصله اطمینان اولی بیشتر از فاصله اطمینان دومی است.

به این ترتیب می‌توان گفت با افزایش سطح اطمینان، دقت برآوردگر فاصله کمتر خواهد شد. البته این موضوع در مورد همه نوع فاصله اطمینان صادق است. برای مثال در فاصله اطمینان مربوط به میانگین جامعه با فرض معلوم بودن واریانس نیز همین نکته به چشم می‌خورد.

نکته: اگر حجم نمونه زیاد باشد، با توجه به قضیه حد مرکزی، می‌توان برای تشکیل فاصله اطمینان برای میانگین جامعه، از روش قبلی استفاده کرد. فقط کافی است که به جای واریانس جامعه از برآورد نمونه‌ای آن کمک گرفت و محاسبات مربوطه را انجام داد.