ترکیب توابع – به زبان ساده
زمانی که یک تابع روی تابعی دیگر عمل کند، دو تابع با یکدیگر ترکیب شدهاند. برای نمونه توابع (f(x و (g(x را در نظر بگیرید. در این حالت میتوان از تابع f بهعنوان ورودی تابع g استفاده کرد.

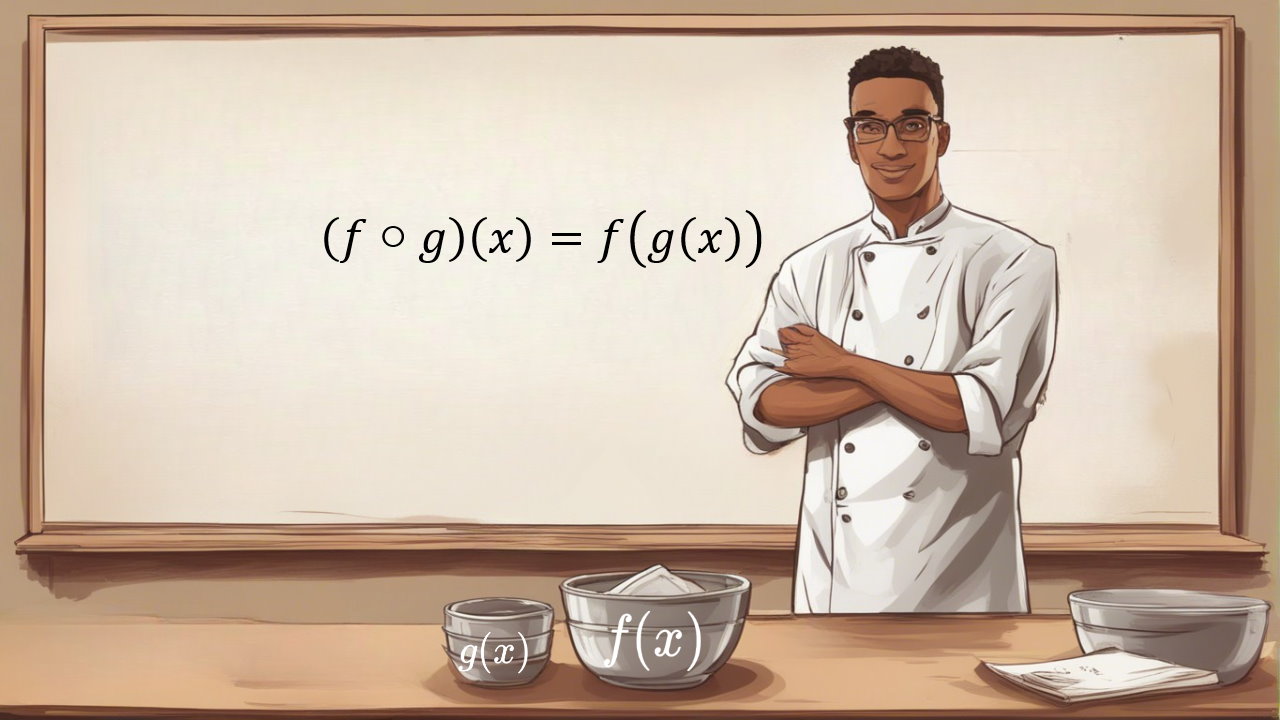

تابعی که در نتیجه وارد شدن f به g بهوجود میآید را با نماد (gof(x نشان میدهند. برای درک بهتر توابع f(x)=2x+3 و g(x)=x2 را در نظر بگیرید. با این فرضیات، هدف ما محاسبه تابع gof است. توجه داشته باشید که x فقط یک نماد محسوب میشود که نشان دهنده ورودی است.
در این شرایط توابع f و g را میتوان بهصورت زیر توصیف کرد.
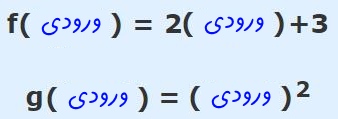
فرض کنید با توجه به این دو تابع میخواهیم حاصل (gof(x را محاسبه کنیم. میدانیم رابطه زیر برقرار است:
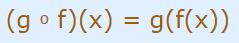
در محاسبه تابعِ (gof(x بایستی توجه داشته باشید که (f(x نقش ورودیِ g را بازی میکند. در این صورت میتوان گفت:
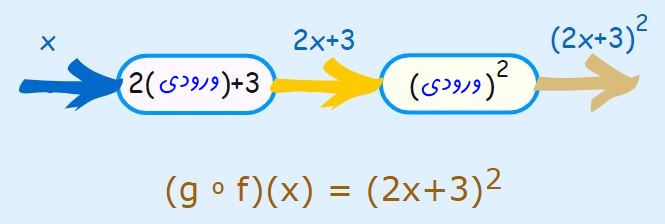
به نظر شما در حالتی عکس، تابع حاصل شده به چه شکل خواهد بود. در حقیقت حاصل تابع (fog(x برابر با چه تابعی است؟ در این حالت g بهعنوان ورودیِ f در نظر گرفته شده و میتوان نوشت:
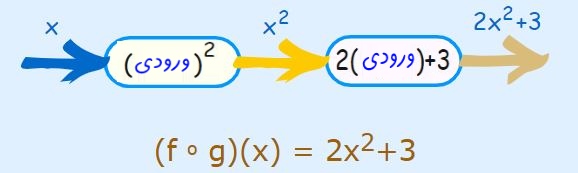
همانطور که دیدید پاسخ بالا با حالت قبل متفاوت است. بنابراین الزاما توابع (fog(x و (gof(x با یکدیگر برابر نیستند.
ترکیب یک تابع با خودش
در برخی از مسائل فیزیکی نیاز است تا یک تابع با خودش ترکیب شود. در مثال ۲ این کار انجام شده است.
مثال ۱
تابع f(x)=2x+3 را در نظر بگیرید. با این فرض، تابع (fof(x را بیابید. بهمنظور بدست آوردن چنین تابعی در ابتدا x را در f قرار داده و پس از آن تابع بدست آمده ((f(x) را دوباره در خودِ (f(x قرار میدهیم. بنابراین میتوان گفت:
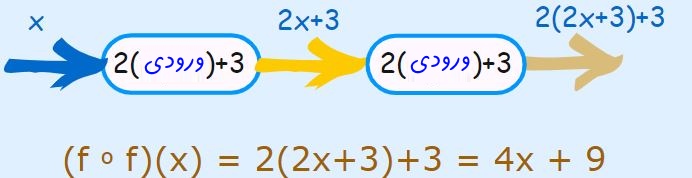
توجه داشته باشید که نیاز نیست همواره از نمودار بالا جهت بدست آوردن تابع ترکیبی استفاده کنیم. میتوان بهطور مستقیم، بهشکل زیر (fof(x را بدست آورد.
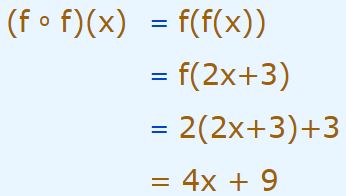
دامنه
در مطلب مفاهیم تابع عنوان شد که دامنه یک تابع برابر با مقادیری است که تابع میتواند به عنوان ورودی دریافت کند. در هنگام ترکیب دو تابع، مقادیر ورودی آنها تغییر میکنند. برای نمونه در دامنه تابع (g(x برابر با مقادیر x است؛ این در حالی است که دامنه تابع (gof(x برابر با مقادیر (f(x است.
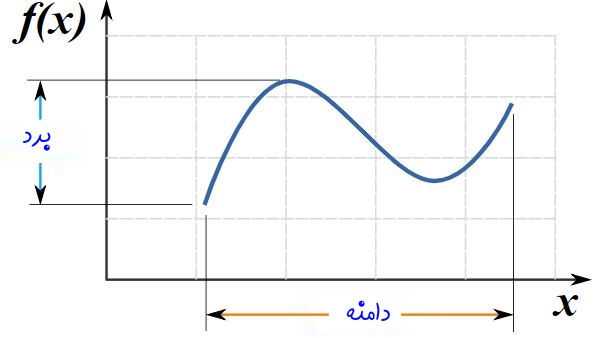
شکل زیر دامنه و برد تابعِ فرضی (f(x را نشان میدهد.
مثال ۲
دامنه تابع در کدام بازه قرار میگیرد؟
بدیهی است که عدد زیر رادیکال نمیتواند منفی باشد. [البته در مباحث پیشرفتهتر ریاضیات با تعریف مفهومی تحت عنوان عدد مختلط، رادیکال عدد منفی نیز قابل محاسبه خواهد بود ولی در بازه اعداد حقیقی نمیتوان از عدد منفی رادیکال گرفت]. در شکل زیر این بازه نشان داده شده است.
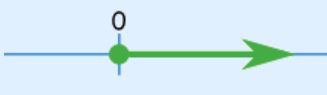
بنابراین دامنه مذکور برابر است با:
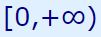
دامنه تابع ترکیبی
جهت محاسبه دامنه یک تابع ترکیبی بایستی دامنه هر دو تابع را به درستی بدست آورید. برای درک بهتر لطفا به مثال زیر توجه فرمایید.
مثال ۳
توابع و را در نظر بگیرید. با این فرض دامنه تابع (gof(x را بیابید. جهت بدست آوردن دامنه تابع مذکور بهترتیب زیر عمل کنید:
- دامنه تمامی اعداد مثبت هستند.
- دامنه تابع کل اعداد حقیقی است.
- تابع (gof(x برابر است با:
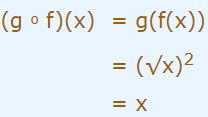
- در رابطه بدست آمده در بالا هر عددی را میتوان قرار داد. اما با توجه به ترکیبی بودن تابع مذکور، عددی را میتوان در آن قرار داد که در تابع f نیز صدق کند. از این رو دامنه تابع fog برابر با اعداد مثبت است.
چرا هر دو دامنه؟
شاید این سوال در ذهن شما شکل گرفته باشد که چرا بهمنظور محاسبه دامنه تابع gof نیاز است تا هر دو دامنه را محاسبه کنیم؟ جهت پاسخ به این سوال، فرض کنید توابع f و g همچون ماشین باشند. تابع f با ذوب کردن یک صفحه امکان ایجاد سوراخی را در سطح بهوجود میآورد. از طرفی تابع g با استفاده از دریل میتواند روی فلز یا چوب، سوراخ مد نظر را ایجاد کند. در شکل زیر مکانیزم توابع مذکور نشان داده شدهاند.
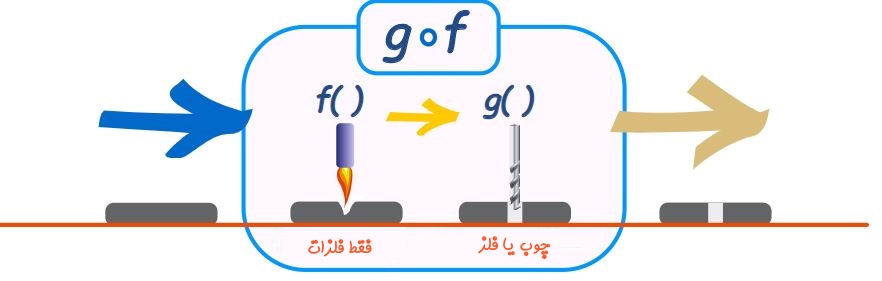
پدیدهای که نهایتا مشاهده میشود سوراخی است که در سطح بهوجود آمده. در ابتدا ممکن است این تصور وجود داشته باشد که ماشین gof میتواند چنین سوراخی را هم در چوب و هم در فلز ایجاد کند.
اما بایستی توجه داشت که اگر سطح چوبی بهعنوان ورودی در نظر گرفته شود، تابع f آن را خواهد سوزاند و سیستم نمیتواند کار کند! در نتیجه جهت بدست آوردن دامنه ماشین (یا همان ورودیهای ماشین)، فرآیندهای رخ داده در کل ماشین بایستی در نظر گرفته شوند.
جداسازی توابع
فرآیند ترکیب دو یا چند تابع را میتوان به شکل عکس نیز انجام داد. در حقیقت ممکن است تابعی داشته باشیم که از ترکیب دو تابع شکل گرفته باشد. در این صورت میتوان از آن دو -یا چند- تابع را بیرون کشیده و به دو تابع رسید.
مثال ۴
تابعی را برابر با در نظر بگیرید. این تابع میتواند از ترکیب دو تابع زیر ساخته شده باشد.
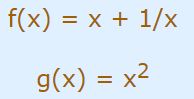
در حقیقت با فرض دو تابع f و g بهشکل بالا تابع gof برابر خواهد بود با:
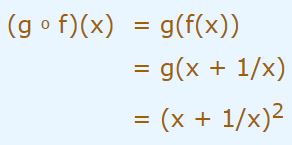
فرآیند جداسازی زمانی مفید است که تابع اصلی بسیار پیچیده باشد.
خلاصه
- زمانی که یک تابع بهعنوان ورودی تابعی دیگر در نظر گرفته شود، دو تابع با هم ترکیب شدهاند.
- جهت محاسبه تابع (gof(x در ابتدا (f(x محاسبه شده، سپس در g قرار میگیرد.
- بهمنظور تحلیل دامنه (gof(x، دامنه f نیز بایستی مدنظر قرار گیرد.
- برخی از توابع را میتوان بهصورت ترکیب دو یا چند تابع در نظر گرفت.
آزمون ترکیب توابع
۱. کدام گزینه به درستی نشاندهنده تفاوت نتیجه ترکیب (gof(x و (fog(x و اهمیت ترتیب توابع است؟
در همه موارد، ترکیب توابع جابجاییپذیر است و نتیجه تغییری نمیکند.
تغییر ترتیب توابع معمولا نتیجه یکسانی دارد و فقط نمادگذاری فرق میکند.
ترتیب توابع مهم است و معمولا (gof(x و (fog(x خروجی متفاوتی میدهند.
در ترکیب توابع، ابتدا هر دو تابع روی x اعمال میشوند و نتیجه یکی است.
ترکیب توابع مانند (gof(x و (fog(x معمولا نتایج متفاوتی دارند، چون ابتدا باید یک تابع روی ورودی اعمال شود و بعد نتیجه آن وارد تابع دیگر گردد.
۲. اگر تابع و تابع باشد، دامنه صحیح برای ترکیب (gof(x چیست؟
تمام اعداد حقیقی
اعداد منفی و مثبت به جز صفر
اعداد مثبت و صفر
اعداد حقیقی نامنفی
برای یافتن دامنه ترکیب (gof(x با توجه به اینکه ابتدا تابع f روی x اعمال میشود باید دامنه f را بررسی کنیم. تابع فقط برای xهای نامنفی (یا همان اعداد مثبت و صفر) تعریف است چون مقدار زیر رادیکال باید غیرمنفی باشد. تابع روی کل اعداد حقیقی تعریف شده است اما چون ورودی اولیه وارد f میشود، باید محدودیت f در نظر گرفته شود. به همین دلیل دامنه ترکیب همان اعداد مثبت و صفر خواهد بود و عبارت «اعداد مثبت و صفر» صحیح است.













مثال چهار جریانش چیه
سلام خدمت شما؛
در این مثال ترکیب دو تابع x + 1/x و x^2 در نظر گرفته شده که حاصل آن را در صورت سوال مشاهده میکنید. در واقع در این سوال بهجای اینکه دو تابع به شما داده شود تا ترکیب آن را پیدا کنید، ترکیب دو تابع به شما داده شده و شما لازم است دو تابع اولیه را پیدا کنید.
از همراهی شما با مجله فرادرس سپاسگزاریم.
اگه ب ما گف تابع f بر روی g رو بنویسم چجوری باید حلش کنیم؟
سلام اگر بیش تر از دو ترکیب تابع داشته باشیم چه نمادی برای نشان دادن این ترکیبات و جود دارد؟
کاش کتابای اموزش پرورش هم اینطوری توضیح میداد
فقط بلدن همه چیزو سخت و بی معنی توضیح بون
توضیحات بسیار شیوا بود مرسی
در مثال چهار :
f(x) = 1 + 1/x
سلام. ضمن تشکر از بازخورد شما، اصلاحات لازم انجام شد.
از همراهیتان با مجله فردارس خوشحالیم.
عالی بود . من دبیر زبان ( 28 سال سابقه ) خیلی علاقمند شدم به ریاضیات بخاطر توضیحات و ساده سازی مطالب . خداوند به شما اجر دهد .