لایه مرزی (Boundary Layer) چیست؟ – از صفر تا صد
در ۸ آگوست ۱۹۰۴ کنفرانسی در دانشگاه Heidelberg آلمان برگزار شد. یکی از افراد شرکت کننده، استادی ۲۹ ساله به نام «لودویگ پرانتل» (Ludwig Prandtl) بود که در دانشگاه Hanover به فعالیت علمی میپرداخت. ارائه پرانتل فقط ۱۰ دقیقه طول کشید، اما همین زمان اندک برای معرفی مفهومی انقلابی در علم کافی بود. ارائه او و مقالهای که در سال ۱۹۰۵ منتشر کرد، مفهومی تحت عنوان «لایهمرزی» (Boundary layer) را در فیزیک معرفی کرد. ۱۹۰۵ سالی بود که آلبرت انیشتین نیز مقاله معروف خود را در مورد نسبیت خاص منتشر کرد. اینگونه بود که دو آلمانی، در یک سال، علم را چندین قدم به جلو بردند.

مقدمه
هنگامی که جریانی به صورت خارجی روی یک جسم حرکت میکند، پدیدههای بسیاری از دیدگاه مکانیک سیالات اتفاق میافتد. واضح است که مشخصههای جریان به شکل سطح وابسته هستند. از طرفی اگر شکل جسم را ثابت فرض کنیم، جریان عبوری روی آن به مشخصههای خود سیال همچون سرعت، جهت حرکت، چگالی، لزجت و ... نیز وابسته خواهد بود.
با انجام آنالیز ابعادی متوجه میشویم که مشخصههای جریان خارجی به اعدادی بیبعد وابسته هستند. در حالت کلی برای عبور یک جریان رو سطح جسم، مهمترین عدد بیبعد، «رینولدز» (Reynolds) است. توجه داشته باشید که فرمول کلی رینولدز به شکل زیر است.
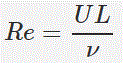
همانطور که در بالا نیز بیان شد، این فرمول به صورت کلی است. اما اجزا تشکیل دهنده آن در موارد مختلف متفاوت هستند. برای نمونه در حالتی که جریانی روی یک استوانه عبور کند، طول L را برابر با قطر استوانه در نظر میگیرند و یا در حالتی که جریانی روی یک صفحه تخت حرکت میکند، این طول برابر با فاصله از لبه صفحه در نظر گرفته میشود.
برای بسیاری از جریانها که دارای رینولدز بالایی هستند، دامنه جریان را میتوان به دو بخش تقسیم کرد:
- لایهمرزی لزج که در نزدیکی سطح جامد تشکیل میشود.
- ناحیه غیرلزج که در بیرون از لایهمرزی است.
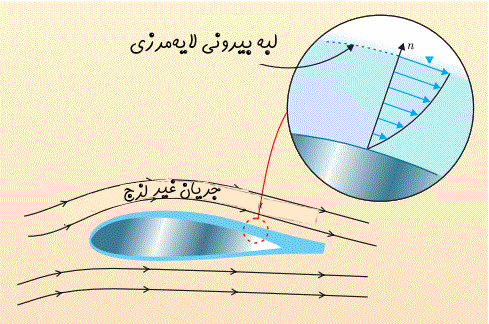
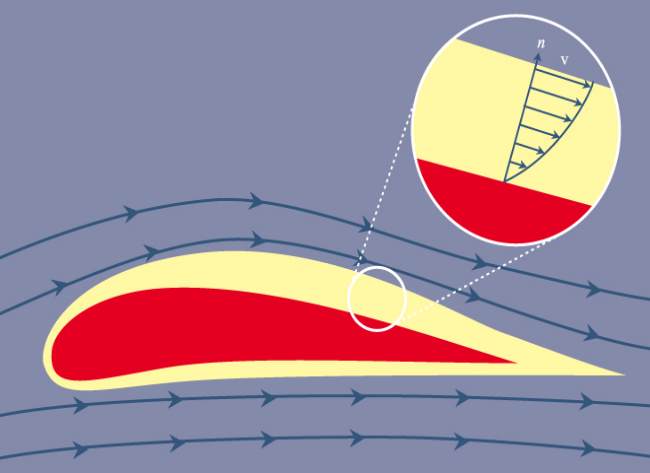
در شکل بالا این دو ناحیه در حالت عبور جریان روی ایرفویل، نشان داده شدهاند.
مفهوم لایه مرزی
تئوری لایه مرزی در سال ۱۹۰۴، توسط پرانتل ارائه شد. این مفهوم ارتباط قابل اتکایی را میان جریان ایدهآل و جریان واقعی ایجاد میکند. سیالات، دارای خاصیتی به نام ویسکوزیته هستند. اثرات اصطکاکی فقط در ناحیهای نزدیک به مرز جسم جامد وجود دارند؛ این ناحیه همان لایهمرزی است.
مطابق با شکل زیر خودرویی در حال حرکت را در نظر بگیرید. واضح است که سرعت ذرات هوای چسبیده به بدنه، برابر با سرعت خودرو هستند. از طرفی اگر به اندازه کافی از خودرو دور شویم، میبینیم که هوای اطراف به صورت ساکن قرار گرفته است. بنابراین در نزدیکی مرز جسم، سرعت نسبی هوا و خودرو صفر و در دوردست این سرعت غیر صفر است. در نتیجه در فاصلهای بسیار اندک از بدنه خودرو گرادیان سرعت تشکیل میشود.

گرادیان سرعت ایجاد شده باعث میشود تا نیرویی اصطکاکی به جسم جامد (یا همان خودرو) وارد شود. این مفهوم را میتوانید در شکل زیر ببینید.
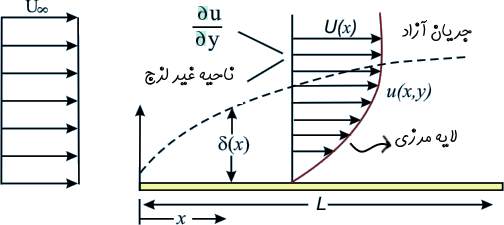
به ناحیهای که در آن سرعت سیال تحت تاثیر نیروهای برشی قرار گرفته، «لایهمرزی» (Boundary Layer) گفته میشود. در این ناحیه سرعت سیال متغیر است. هنگامی که جریانی رو سطح به حرکت در میآید، در ابتدا لایهمرزی به صورت «لایهای» (Laminar) است. همچنین پس از آنکه که جریان بخشی از مرز جامد را طی میکند، ضخامت لایهمرزی رشد کرده و حرکت سیال ناپایدارتر میشود. در این حالت جریان شروع به توربولانس شدن میکند. گفتنی است که در ناحیه توربولانس، ذرات سیال به صورت تصادفی حرکت میکنند.
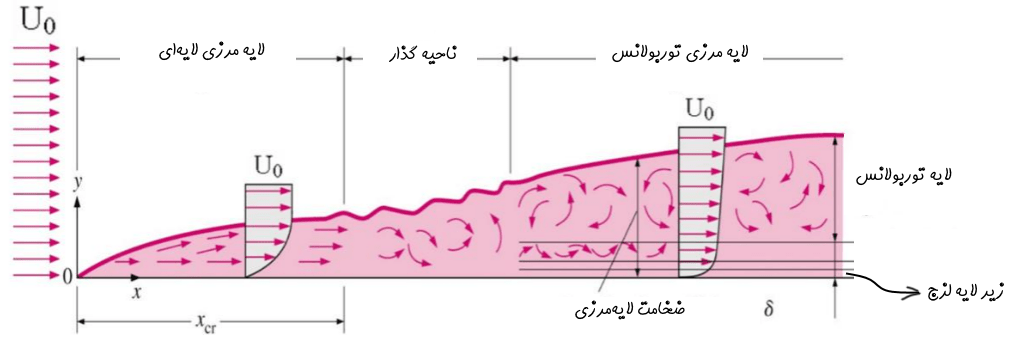
پس از توربولانسی شدن لایهمرزی، همچنان بخش بسیار نازکی از سیال که به مرز جسم چسبیده، به صورت لایهای باقی میماند. به این لایه «زیر لایه لزج» (Viscous sublayer) گفته میشود. قبل از مطالعه ادامه مطلب حتما بخشهای مختلف لایهمرزیِ شکل بالا را مورد توجه قرار دهید.
تعاریف بسیاری به منظور توصیف ضخامت لایهمرزی (این ضخامت با نماد δ نشان داده میشود) ارائه شده. بنیادیترین آنها، ضخامت لایهمرزی را فاصلهای تعریف میکند که در آن گرادیان سرعت وجود دارد.
برای توصیف ضخامت لایهمرزی، شکل شماره ۱ را که در زیر آمده در نظر بگیرید. ضخامت لایهمرزی را به صورت زیر تعریف میکنیم:
به فاصلهای از سطح جامد که سرعت سیال در آن نقطه ۹۹ درصد سرعت جریان آزاد باشد (u=0.99U)، ضخامت لایهمرزی (δ) گفته میشود.
با توجه به تعریف ارائه شده برای δ، میتوان ضخامت جابجاییِ *δ۱ را به شکل زیر تعریف کرد.
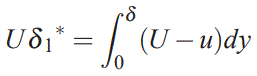
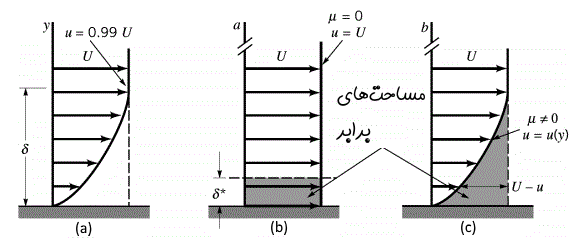
برای درک مفهوم ضخامت جابجایی تصور کنید که دبی جریان در هر دو شکل a و b برابر باشند. از آنجایی که سرعت در تمامی دامنه، در شکل b برابر با U در نظر گرفته شده، بنابراین بهمنظور برابری دبی جریان در دو شکل a و b میتوان مرز جسم جامد را کمی بالاتر تصور کرد.
همچنین ضخامت لایهمرزی مومنتوم به شکل زیر قابل تعریف است.
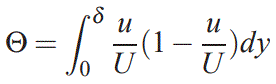
همچون ضخامت جابجایی در این تعریف نیز فرض شده در تمامی دامنه جریان، سرعت برابر با U باشد. در ادامه در مورد هریک از این مفاهیم بیشتر بحث میشود و از آنها در تحلیل لایهمرزی استفاده خواهد شد.
تحلیل مقیاسی
پرانتل معادلات حرکت سیال، درونِ لایهمرزی را با استفاده از تحلیل اندازه جملات معادله نسبت به یکدیگر، انجام داد. به منظور توضیح بیشتر، معادله مومنتوم سیال را در راستای x به صورت زیر در نظر بگیرید [ رابطه پایین معادله ناویر-استوکس در راستای x است. هماکنون درک خود رابطه مهم نیست. در مطلبی به صورت مجزا معادلات ناویر-استوکس را توضیح خواهیم داد].
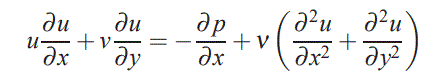
رابطه بالا در حقیقت قانون دوم نیوتن برای سیال است. از ریاضیات میدانید که عبارات سمت چپ این معادله، شتاب ذرات سیال را نشان میدهند؛ همچنین عبارات سمت راست آن نیروهای وارد به حجم کنترل را بیان میکنند. پرانتل در اولین فرضِ مهم خود، ضخامت لایه مرزی δ را بسیار کوچکتر از طول L در نظر گرفت. طول L، از مرتبه اندازه جسم در راستای جریان است.
ابتدا به ساکن، بایستی برای هر کمیت مقداری مرجع تعریف کنیم. این مقادیر از جنس هم هستند. برای نمونه، سرعتِ مرجع را برابر با U فرض میکنیم. U نشان دهنده سرعت جریان آزاد است، که مقداری ثابت محسوب میشود. همچنین طول مرجع را برابر با L در نظر میگیریم. با توجه به تعاریف انجام شده میتوان گزارههای زیر را مطرح کرد:
اندازه عبارت از مرتبه است. بنابراین مرتبه عبارت نیز برابر با خواهد بود.
به همین شکل میتوان گفت:
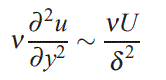
با توجه به این که δ بسیار کوچکتر از L است، داریم:
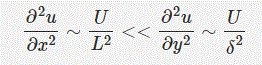
فرض مهم دیگری که پرانتل انجام داد این بود که نیروهای اینرسی و برشی (یا همان ویسکوزی) از یک مرتبه هستند. با استفاده از این روش میتوان مرتبه ضخامت را یافت. با برابر قرار دادن دو عبارت بالا داریم:
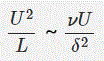
علامت «~» به معنای هم مرتبه بودن دو عبارت است. با مرتب کردن عبارت بالا مرتبه ضخامت به صورت زیر محاسبه میشود.
![]()
علامت O در رابطه بالا نشان دهنده مرتبه است. بنابراین همانطور که در بالا نیز نشان داده شد، ضخامت لایهمرزی با رابطه دارد. در شکل زیر ضخامت لایهمرزی و پروفیل جریان در مکانهای مختلف نشان داده شده است.
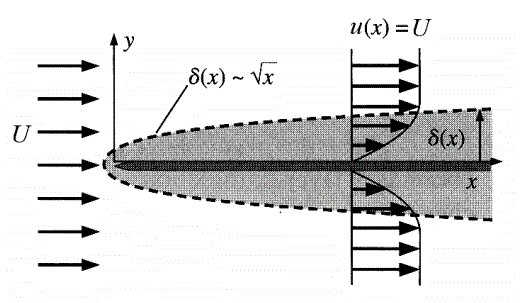
با فرض u=0.99U در لبه لایهمرزی رابطه دقیق ضخامت لایهمرزی به صورت زیر یافت میشود.
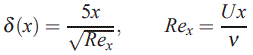
در ادامه نحوه بدست آمدن فرمول ضخامت لایهمرزی را شرح خواهیم داد.
معادلات مومنتوم در لایهمرزی
معمولا برای محاسبه ضخامت لایهمرزی و یا دیگر پارامترهای مرتبط با این ناحیه، میتوان از روشهای انتگرالگیری بهره برد. در نتیجه تحلیل لایهمرزی را با انتگرالگیری از معادلات پیوستگی و مومنتوم آغاز میکنیم. در ابتدا شکل زیر را در نظر بگیرید.
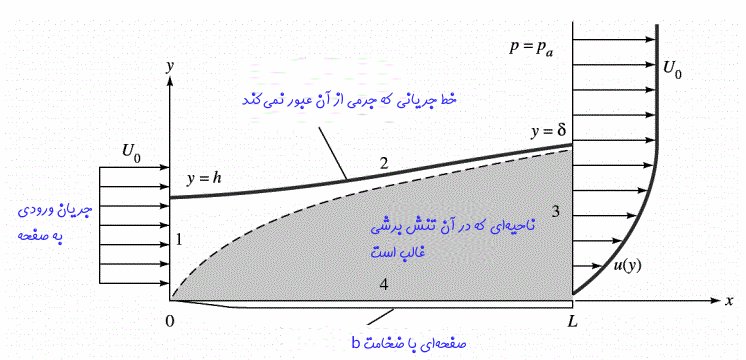
همانطور که در مطلب سینماتیک سیالات نیز بیان کردیم، هیچگاه از خطوط جریان، جرمی عبور نمیکند. بنابراین معادله نیروی وارد شده به حجم کنترل تشکیل شده از مرز جسم و خط جریان شماره ۲، را میتوان با استفاده از انتگرال حجمی زیر محاسبه کرد.
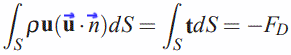
توجه داشته باشید که در تمامی فرمولها U و U0 با هم برابر هستند.
در رابطه بالا FD برابر با نیروی درگ وارد شده به حجم کنترل و عبارت سمت چپ، انتگرال تغییرات مومنتوم را نشان میدهد. همانطور که در شکل نیز میبینید فقط از مرزهای ۱ و ۳ جریان جرمی عبور میکند، بنابراین با باز کردن رابطه بالا میتوان آن را به صورت زیر بازنویسی کرد.
![]()
رابطه بالا نیرو را در واحد b بیان کرده، از این میتوان آن را در ضخامت نیز ضرب کرد [ضرب کردن یا نکردن رابطه بالا در b تفاوتی در محاسبه ضخامت لایهمرزی ایجاد نمیکند]. با ساده کردن رابطه بالا به فرمول زیر میرسیم:
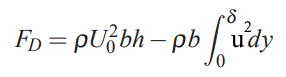
در رابطه بالا b برابر با ضخامت صفحه است. حال میتوان معادله پیوستگی را به صورت زیر نوشت [این معادله بیان میکند که جرم ورودی به حجم کنترل برابر با جرم خروجی از آن است].
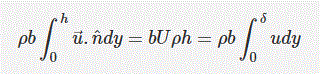 با توجه به رابطه بالا h برابر است با:
با توجه به رابطه بالا h برابر است با:
با جایگذاری h در معادله (۱)، نیروی FD به صورت زیر محاسبه میشود.
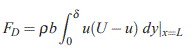
معادله بالا را میتوان بر حسب ضخامت مومنتوم و مطابق با رابطه زیر بیان کرد:
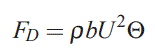
ضخامت مومنتومِ Θ درگ کلی صفحه را نشان میدهد. این نیرو را میتوان با استفاده از انتگرالگیری از تنش برشی نیز محاسبه کرد. در عبارت زیر نیروی بدست آمده از این دو روش با یکدیگر برابر قرار داده شدهاند.
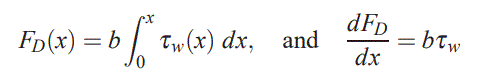
رابطه بالا را میتوان بر حسب ضخامت مومنتوم و به شکل زیر بیان کرد:
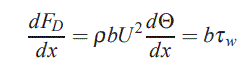
نهایتا میتوان نوشت:
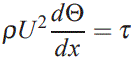
رابطه بالا تحت عنوان «معادله انتگرالی مومنتوم برای جریان لایهمرزی» شناخته میشود. نیروی وارد به هر سیستم سیالاتی را میتوان با استفاده از ضریب اصطکاک سطح نیز بیان کرد. در این مسئله ضریب اصطکاک Cf را به صورت زیر تعریف میکنیم.
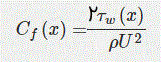
بر مبنای تعریف بالا، معادله (۲) را میتوان به شکل زیر بازنویسی کرد.
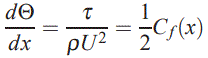
رابطه بالا یک معادله دیفرانسیل است که با حل آن میتوان پروفیل (u(y را در لایهمرزی بدست آورد. برای محاسبه (u(y معمولا آن را به صورت تابعی از y/δ در نظر میگیرند، سپس با جایگذاری (u(y در نظر گرفته شده در شرایط مرزی، u بدست میآید. برای درک بهتر موضوع میتوانید به مثال زیر توجه فرمایید.
مثال
مطابق شکل زیر جریانی را روی سطح تختی در نظر بگیرید. با فرض اینکه پروفایل u تابع از y/δ باشد، تنش برشی و ضریب اصطکاک را در راستای x محاسبه کنید.
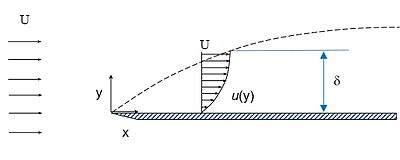
در چنین مسائلی معمولا u را به صورت یک چندجملهای از مرتبه n در نظر میگیرند. در این مثال فرض میکنیم که وابستگی u نسبت y/δ از درجه ۳ است، بنابراین میتوان گفت:
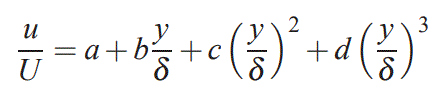
این رابطه شامل چهار مجهول a, b, c, d است؛ از این رو بایستی ۴ شرط مرزی نیز برای آن تعریف کنیم. شرایط مرزی این مسئله در ادامه ذکر شدهاند.
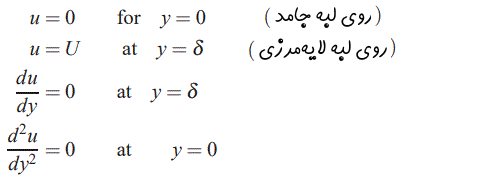
با اعمال این ۴ شرط مرزی در (u(y در نظر گرفته شده، به ۴ رابطه زیر میرسیم:
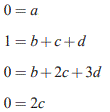
با حل این چهار معادله، مقادیر a و c برابر با صفر، d و b به ترتیب برابر با ۱/۲- و ۳/۲ بدست میآیند. بنابراین شکل پروفایل u در لایهمرزی به صورت زیر است.
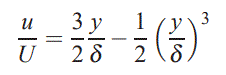
با استفاده از پروفیل بدست آمده میتوان ضخامت مومنتوم را به شکل زیر محاسبه کرد.
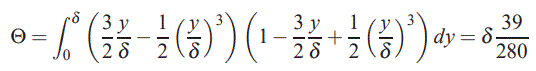
در نتیجه تنش برشی نیز با محاسبه گرادیان u در راستای y محاسبه میشود.
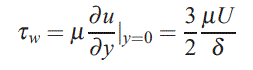
با جایگذاری دو رابطه بالا در معادله شماره (۳)، تابع (δ(x بر حسب x به شکل زیر محاسبه میشود.
![]()
در نتیجه
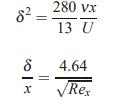
اگر به یاد داشته باشید در بالا گفتیم که رابطه δ را به صورت در نظر میگیرند؛ این مقدار همان عدد نزدیک به ۴.۶ است که گرد شده.
با بدست آمدن (δ(x اکثر پارامترها نیز محاسبه خواهند شد. برای نمونه میتوان ضریب اصطکاک را به صورت زیر بدست آورد.
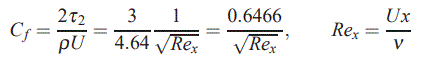
^^













شرط مرزی چهارم چگونه به دست اومده؟!
سلام
مرجع مورد استفاده برای مطالب رو بفرمائید.ممنون
سلام، وقت شما بخیر؛
منابع مورد استفاده برای هر یک از مطالب در انتهای آنها و پس از مطالب پیشنهادی ذکر شدهاند.
از اینکه با مجله فرادرس همراه هستید از شما سپاسگزاریم.
بسیار عالی ممنون از شما و همکاران محترم
سلام
تبریک می گم
تو این زمینه بهترین هستین
سایتتون هم زیباست
خیلی خیلی ممنونم از فرادرس فقط مشکلی که تو فیلم های آموزشی وجود داره خسته کننده بودنش هست که مربوط میشه به صداوتصویر یکنواخت اگر بعضا تصویر استاد کنارش صفحه ظاهر میشد یا چند ثانیه فیلم مرتبط یا…پخش میشد خیلی بهتر بود.
عالی
ممنون .