منطق ترکیبی به زبان ساده – بخش نهم: تفریق گر باینری
«تفریقگر باینری» (Binary Subtractor) نوع دیگری از مدارهای محاسباتی ترکیبی است. این مدار وظیفهای عکس جمعکنندهی باینری بر عهده دارد که در گذشته آن را به طور کامل بررسی کردیم.
همانگونه که از نام آن پیداست، تفریقگر باینری یک مدار تصمیمگیری است که دو عدد باینری را از یکدیگر کم میکند؛ به عنوان مثال X - Y شده و اختلاف این دو در خروجی قرار میگیرد.
برخلاف جمعکنندهی باینری که دو بیت خروجی SUM و CARRY تولید میکند، تفریقگر باینری با استفاده از یک بیت «قرضی» یا BORROW) B) از ستون قبلی، یک خروجی «اختلاف» یا DIFFERENCE) D) تولید میکند. لذا واضح است که فرآیند تفریق برعکس فرآیند جمع اتفاق میافتد.
- بخشهای اول، دوم، سوم، چهارم، پنجم، ششم، هفتم و هشتم این مجموعه مطلب را میتوانید با کلیک روی هر یک از لینکهای مربوطه مطالعه کنید.
از قبل میدانیم که علامت منفی (-) برای محاسبهی حاصل تفریق به کار میرود و وقتی یک عدد از عدد دیگر کم میشود، اگر رقم مفروق از مفروق منه بزرگتر باشد، به یک رقم قرضی احتیاج است. به مثال زیر که تفریق سادهی میان دو عدد دهدهی را نشان میدهد توجه کنید.

در ستون اول از آنجا که 3 از 8 کوچکتر است، نمیتوانیم به طور مستقیم 8 را از 3 کم کنیم، لذا باید یک عدد 10 (مبنای اعداد) از ستون سمت چپ قرض گرفته و به مفروق منه اضافه کنیم. عملیاتی که ذکر شد، همان کاری است که در ریاضیات پایه انجام میدادیم.
برای تفریق اعداد باینری نیز از همان شیوهی تفریق اعداد دهدهی استفاده میشود؛ اما از آنجایی که اعداد باینری مبنای 2 دارند، در نمایش آنها تنها از ارقام 0 و 1 استفاده میشود. رقم قرضی برای تفریق اعداد باینری همواره رقم 1 است.
تفریق باینری
تفریق باینری را به روشهای مختلفی میتوان انجام داد اما قوانین حاکم بر تمامی این روشها یکسان هستند. میدانیم که اعداد باینری تنها دو رقم متفاوت دارند و لذا چهار حالت مختلف ممکن است پیش بیاید. تفریق 0 از ارقام 0 و 1 تغییری در نتیجه ایجاد نمیکند، یعنی 0 = 0 – 0 و 0 = 1 – 0 است. از طرفی تفریق 1 از 1 نیز مساوی 0 است. اما برای آخرین حالت یعنی تفریق 1 از 0 یا 0 – 1 به رقم قرضی احتیاج است.
تفریق باینری دو بیت

در مثال سادهی بالا، اگر از بیت قرضی صرف نظر کنیم نتیجهی تفریق باینری دقیقاً برابر با خروجی یک گیت XOR خواهد بود. میتوان بیت قرضی خروجی را با نماد B و یکی از ورودیها را نیز با نماد B نشان داد؛ اما ممکن است این موضوع ما را به اشتباه بیندازد. لذا در ادامهی این مقاله بیتهای ورودی را با X و Y نشان میدهیم؛ که X بیت مفروق منه و Y بیت مفروق است. با این حساب جدول درستی برای تفریقگر باینری تک بیتی به صورت زیر خواهد بود.
گیت XOR با دو ورودی

همانند جمعکنندهی باینری، اختلاف بین دو رقم تنها وقتی 1 میشود که ورودیها یکسان نباشند. تا بدین جای کار خروجی D را با گیت XOR پیادهسازی کردهایم، اما لازم است در حالتی که X = 0 و Y = 1 است، بیت قرضی خروجی را نیز به روشی نشان دهیم. متأسفانه گیت منطقی استانداردی که چنین خروجی را تولید کند وجود ندارد.
اما میدانیم اگر ورودیهای گیت AND یک باشند، خروجی آن نیز یک میشود. لذا اگر در سر راه ورودی X یک گیت NOT قرار داده و خروجی این گیت را همراه با ورودی Y، AND کنیم، بیت قرضی خروجی هنگامی که X = 0 و Y = 1 باشد تولید میشود.

لذا با ترکیب گیت XOR و مداری که در بالا ساخته شد، مدار یک تفریقگر باینری ساده ایجاد میشود که به نام «نیم تفریقگر» (Half Subtractor) نیز شناخته میشود.
مدار نیم تفریقگر باینری
نیم تفریقگر یک مدار منطقی است که بر روی دو بیت باینری عملیات تفریق انجام میدهد. این مدار دو خروجی اختلاف و بیت قرضی تولید میکند که برای طبقهی بعدی مدار کلی استفاده میشود.
نیم تفریقگر همراه با بیت قرضی خروجی
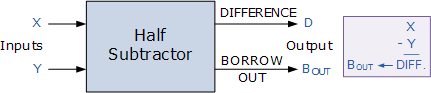
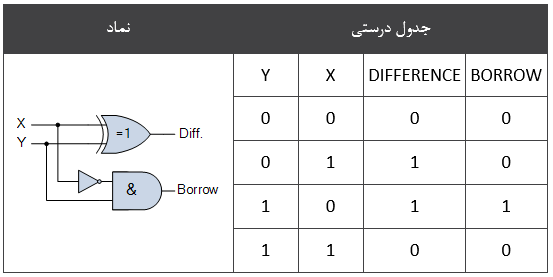
از جدول درستی نیم تفریقگر میتوان متوجه شد که خروجی اختلاف یا DIFFERENCE) D) نتیجهی گیت XOR بوده و خروجی قرضی یا Borrow-out) Bout) نتیجهی ترکیب گیتهای NOT و AND است. لذا عبارت بولی که میتوان برای توصیف نیم تفریقگر به کار برد به صورت زیر است.
برای بیت اختلاف:

برای بیت قرضی:

اگر عبارتهای بولی نیم تفریقگر را با نیم جمعکننده مقایسه کنیم، میفهمیم که عبارتهای استفاده شده برای SUM (در جمعکننده) و DIFFERENCE (در تفریقگر) دقیقاً یکسان هستند که به خاطر استفاده از گیت XOR است. عبارتهای بولی توصیفکنندهی بیت BORROW در تفریقگر و بیت CARRY در جمعکننده نیز شباهت بسیار زیادی به یکدیگر دارند. لذا برای تبدیل یک نیم جمعکننده به یک تفریقگر تنها باید ورودی مفروق منه (X) را معکوس کنیم.
یکی از بزرگترین ایرادات نیم تفریقگر نداشتن پایهای برای «قرضی ورودی» از مدار قبلی است. این موضوع در مواقعی که بخواهیم دادههای چند بیتی را از هم کم کنیم ما را با مشکل مواجه میکند. برای حل این مشکل مداری به نام «تمام تفریقگر» (Full Subtractor) طراحی شده است که در این مدار قرضی ورودی از طبقهی قبلی مدار نیز استفاده شده است.
مدار تمام تفریقگر باینری
تفاوت اصلی میان تمام تفریقگر و نیم تفریقگر در این است که تمام تفریقگر علاوه بر دو پایهی ورودی برای ورودیهای X (مفروق منه) و Y (مفروق)، یک پایهی ورودی نیز برای بیت قرضی ورودی یا Borrow-in) Bin) دارد. از طریق این پایه بیت قرضی تولید شده توسط تفریقگر طبقهی قبلی دریافت میشود.
بلوک دیاگرام تمام تفریقگر
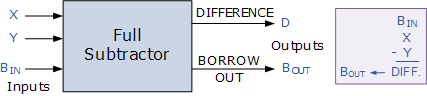
مدار ترکیبی تمام تفریقگر بر روی سه بیت عمل تفریق انجام داده و دو خروجی اختلاف (D) و قرضی خروجی (Bout) تولید میکند. همانند مدار جمعکنندهی باینری، تمام تفریقگر باینری را نیز میتوان با ترکیب دو نیم تفریقگر باینری ساخت؛ برای این کار تنها کافی است قرضی خروجی از نیم تفریقگر اولی را با قرضی خروجی نیم تفریقگر دومی XOR کنیم. از طرفی خروجی اختلاف اولین نیم تفریقگر به ورودی مفروق منه دومین نیم تفریقگر داده میشود. برای درک بهتر این موضوع به شکل زیر توجه کنید.
دیاگرام منطقی تمام تفریقگر

همانگونه که از مدار تمام تفریقگر بالا مشخص است، دو نیم تفریقگر با یکدیگر کسکد شدهاند. از آنجایی که سه ورودی داریم، جدول درستی تمام تفریقگر هشت حالت مختلف خواهد داشت. ورودیهای این مدار عبارتند از BIN و دو بیت دادهی X و Y.
جدول درستی تمام تفریقگر

با توجه به جدول بالا عبارت بولی که برای توصیف تمام تفریقگر استفاده میشود به صورت زیر است.
برای بیت اختلاف (D) داریم:

که آن را میتوان به صورت زیر نیز ساده کرد:

برای بیت قرضی خروجی (BOUT) داریم:

که آن را میتوان به صورت زیر نیز ساده کرد:
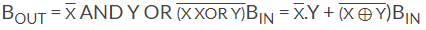
تفریقگر باینری n بیتی
همانند جمعکنندهی باینری، میتوانیم n تا تفریقگر باینری 1 بیتی را با یکدیگر متصل یا کسکد کرده و یک تفریقگر باینری n بیتی بسازیم. از طرفی پیش از این اشاره کرده بودیم که برای تبدیل یک جمعکنندهی باینری به تفریقگر باینری تنها کافی است یکی از ورودیها را معکوس کنیم.
لذا میتوان به راحتی با استفاده از یک جمعکنندهی n بیتی و n تا گیت NOT عملیات تفریق را انجام داد. برای این کار تنها کافی است «مکمل دو» (two’s complement) عدد مفروق را حساب کرده و ورودی نقلی کم ارزشترین بیت را 1 کنیم.
تفریقگر باینری به کمک مکمل دو

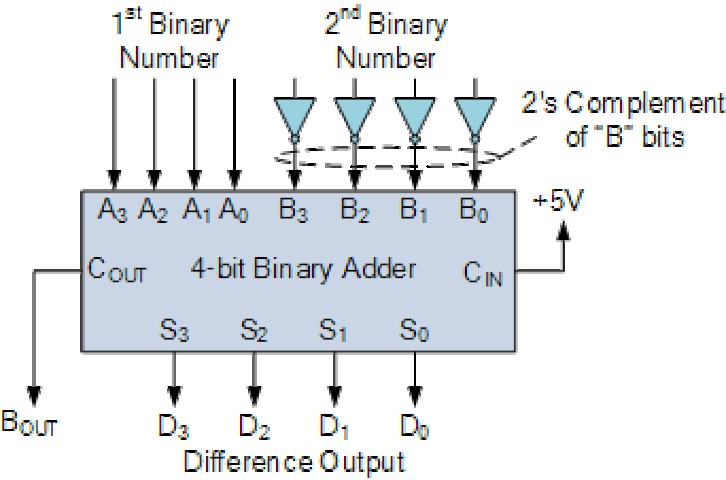
واضح است که X – Y مساوی است با (X + (-Y که همان X به علاوهی مکمل دو Y است. لذا به سادگی میتوان با استفاده از یک آیسی تمام جمعکنندهی 4 بیتی مثل 74LS283 یا CD4008 و اعمال مکمل دو بر روی مفروق (ورودی B) عملیات تفریق بین دو عدد 4 بیتی را انجام داد.
اگر بخواهیم دوباره از جمعکنندهی 4 بیتی برای عملیات جمع استفاده کنیم، تنها لازم است پایهی نقلی ورودی (CIN) را 0 کنیم. لذا آیسی هایی مانند 74LS83 یا 74LS283 دارای یک پایهی ورودی کنترلی برای استفاده به عنوان جمعکننده یا تفریقگر و سوئیچ بین این دو کارکرد هستند.
برای مطالعه بخش دهم از مجموعه مقالات «منطق ترکیبی» بلاگ فرادرس میتوانید از این لینک استفاده کنید؛ ضمناً اگر مطلب بالا برای شما مفید بوده است، ممکن است آموزشهای زیر نیز برایتان کاربردی باشند.
- مجموعه آموزش های مدارهای منطقی (طراحی دیجیتال)
- گنجینه فرادرس های آموزش الکترونیک دیجیتال و سیستم های برنامه پذیر
- مجموعه آموزشهای مهندسی برق
- آموزش جامع سیستمهای باینری
^^










سلام، میشه بگید خروجی های جدول درستی تفریق کننده کامل چطوری به دست اومده یا یه ویدیو برای توضیحش بذارید لطفا🙏🙏🙏🙏