حذف عنصر از درخت جستجوی دودویی – به زبان ساده

در این مطلب، روش حذف عنصر از درخت جستجوی دودویی بیان شده است. فرض می‌شود یک درخت جستجوی دودویی وجود دارد. هنگامی که یک «گره» (Node) از این درخت حذف می‌شود، سه احتمال وجود دارد.

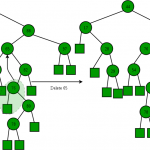
۱. گره حذف شده، برگ است. به سادگی می‌توان این گره را از درخت حذف کرد.

              50                            50
           /     \         delete(20)      /   \
          30      70       --------->    30     70 
         /  \    /  \                     \    /  \ 
       20   40  60   80                   40  60   80

۲. گره حذف شده، تنها یک فرزند دارد. فرزند گره در جای خود گره کپی و فرزند آن حذف می‌شود.

              50                            50
           /     \         delete(30)      /   \
          30      70       --------->    40     70 
            \    /  \                          /  \ 
            40  60   80                       60   80

۳. گره‌ای که باید حذف شود، دارای دو فرزند است. به ترتیب، جانشین گره باید پیدا شود. محتوای جانشین به ترتیب، در گره کپی و جانشین به ترتیب حذف می‌شود. توجه به این نکته لازم است که جد به ترتیب نیز قابل استفاده است.

              50                            60
           /     \         delete(50)      /   \
          40      70       --------->    40    70 
                 /  \                            \ 
                60   80                           80

مساله مهمی که باید به آن توجه داشت این است که جانشین مرتب تنها هنگامی مورد نیاز است که فرزند راست خالی نباشد. در این شرایط خاص، جانشین مرتب را می‌توان با پیدا کردن کمترین مقدار در فرزند سمت راست گره به دست آورد.

حذف عنصر از درخت جستجوی دودویی در ++C

فیلم آموزش برنامه نویسی با تبدیل فلوچارت به کد با فلوگوريتم Flowgorithm + گواهینامه در فرادرس

کلیک کنید

حذف عنصر از درخت جستجوی دودویی در جاوا

حذف عنصر از درخت جستجوی دودویی در پایتون

فیلم آموزش نکات برنامه نویسی پایتون و حل مسائل الگوریتمی در فرادرس

کلیک کنید

حذف عنصر از درخت جستجوی دودویی در #C

خروجی قطعه کدهای بالا به صورت زیر است.

Inorder traversal of the given tree
20 30 40 50 60 70 80
Delete 20
Inorder traversal of the modified tree
30 40 50 60 70 80
Delete 30
Inorder traversal of the modified tree
40 50 60 70 80
Delete 50
Inorder traversal of the modified tree
40 60 70 80

پیچیدگی زمانی

پیچیدگی زمانی بدترین حالت از عملیات حذف برابر با (O(h است که در آن، h ارتفاع درخت جستجوی دودویی محسوب می‌شود. در بدترین حالت، ممکن است نیاز باشد از ریشه به عمیق‌ترین گره برگ رفت. ارتفاع درخت دارای چولگی ممکن است n و پیچیدگی زمانی عملیات حذف ممکن است (O(n باشد.

روش دوم حذف یک گره از درخت جستجوی دودویی

اکنون، روش بیان شده در بالا بهینه‌سازی می‌شود. در کد بازگشتی بالا، به صورت بازگشتی ()delete برای جانشین فراخوانی می‌شد. می‌توان از فراخوانی بازگشتی با نگهداری گره والد جانشین اجتناب کرد، بنابراین می‌توان جانشین را با NULL کردن فرزند والد به سادگی حذف کرد. جانشین همیشه یک گره فرزند است.

فیلم آموزش نکات برنامه نویسی پایتون و حل مسائل الگوریتمی در فرادرس

کلیک کنید

حذف عنصر از درخت جستجوی دودویی در ++C

خروجی قطعه کد بالا به صورت زیر است.

Inorder traversal of the given tree 
20 30 40 50 60 70 80 
Delete 20
Inorder traversal of the modified tree 
30 40 50 60 70 80 
Delete 30
Inorder traversal of the modified tree 
40 50 60 70 80 
Delete 50
Inorder traversal of the modified tree 
40 60 70 80

فیلم مجموعه آموزش برنامه نویسی – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• برنامه تشخیص اعداد اول در پایتون — به زبان ساده
• برنامه تجزیه عدد به عوامل اول آن — به زبان ساده
• حل مساله رنگ‌آمیزی گراف با الگوریتم پس گرد — به زبان ساده

^^