تشخیص ناهنجاری با استفاده از داده کاوی — بررسی موردی همراه با کدهای پایتون

۱۳۰۴ بازدید

آخرین به‌روزرسانی: ۲۵ اردیبهشت ۱۴۰۲

زمان مطالعه: ۹ دقیقه

دانلود PDF مقاله

تشخیص ناهنجاری با استفاده از داده کاوی — بررسی موردی همراه با کدهای پایتون

در داده‌کاوی (Data Mining)، به فرآیند شناسایی نمونه‌ها، رویدادها یا مشاهداتی که با الگوها یا دیگر نمونه‌های موجود در مجموعه داده مطابقت نداشته باشند، «تشخیص ناهنجاری» (Anomaly detection) یا «تشخیص دورافتادگی» (Outlier Detection) گفته می‌شود. معمولا ناهنجاری‌ها بسته به نوع مساله، مربوط به کلاهبرداری بانکی، حملات سایبری ساختاریافته، مشکلات پزشکی یا وجود خطا در متن هستند. به ناهنجاری، «دورافتادگی»، الگوی نوظهور، «نویز» (noise)، انحراف (deviation) و استثنا (exception) نیز گفته می‌شود.

فهرست مطالب این نوشته

کاربردها

انواع ناهنجاری

روش‌های تشخیص ناهنجاری

ساخت یک تشخیص دهنده ناهنجاری ساده با استفاده از فیلتر پایین گذر

به طور کلی، در بحث تشخیص سو استفاده و نفوذ در شبکه‌های کامپیوتری، نمونه داده‌های جذاب نه موارد نادر بلکه انفجارهای غیر منتظره در فعالیت‌ها هستند. این مفهوم با تعریف متداول آمار از دورافتادگی (به عنوان یک نمونه نادر) مطابقت ندارد و ممکن است روش‌های تشخیص دورافتادگی (که معمولا نظارت نشده هستند) برای تشخیص ناهنجاری در داده‌ها با شکست مواجه شوند. این در حالیست که الگوریتم‌های تحلیل خوشه اغلب قادر به شناسایی خوشه‌های کوچکی (Micro Clusters) هستند که به وسیله داده‌های ناهنجار شکل گرفته‌اند.

تشخیص ناهنجاری

سه دسته گسترده از روش‌های تشخیص ناهنجاری وجود دارد. روش‌های تشخیص ناهنجاری نظارت نشده، قادر به تشخیص ناهنجاری‌ها در مجموعه داده‌های تست بدون برچسب با این فرض هستند که اکثریت نمونه‌های داده در مجموعه داده بهنجار محسوب می‌شوند و به آنچه در مجموعه داده موجود است شباهت دارند.

فیلم آموزش اصول و روش های متن کاوی Text Mining در فرادرس

کلیک کنید

روش‌های تشخیص ناهنجاری نظارت شده، نیازمند یک مجموعه داده دارای برچسب «بهنجار» (Normal) یا «ناهنجار» (Abnormal) و آموزش یک دسته‌بند هستند (تفاوت کلیدی با دیگر مسائل دسته‌بندی آماری طبیعت نامتوازن ذاتی تشخیص دورافتادگی است). روش‌های تشخیص ناهنجاری نیمه نظارت شده مدل رفتار طبیعی یک مجموعه داده بهنجار را از یک مجموعه داده (بهنجار) ارائه شده می‌سازند و سپس درست‌نمایی (likelihood) یک نمونه تست به‌منظور تولید شدن توسط مدلی که مرحله یادگیری را طی کرده ارزیابی می‌کنند.

کاربردها

تشخیص ناهنجاری در طیف وسیعی از کاربردها مانند تشخیص نفوذ، تشخیص ناهنجاری، تشخیص خطا، سیستم‌های نظارت بر سلامت (تشخیص تومور بدخیم در تصویر MRI)، تشخیص رویداد در شبکه‌های حسگر، و تشخیص اختلالات اکوسیستم مورد استفاده قرار می‌گیرد.

فیلم آموزش روش های تحلیل داده های پرت (Outlier Analysis) در داده کاوی (رایگان) در فرادرس

کلیک کنید

همچنین در پیش‌پردازش داده‌ها به منظور حذف داده‌های ناهنجار از مجموعه داده، که اغلب به لحاظ آماری منجر به رشد قابل توجهی در صحت می‌شود مورد استفاده قرار می‌گیرند.

کاربردهای تشخیص ناهنجاری

انواع ناهنجاری

پیش از ورود به مباحث تخصصی‌تر تشخیص ناهنجاری، بهتر است که مرزهایی برای تعریف ناهنجاری در نظر گرفته شود. ناهنجاری‌ها را می‌توان در حالت کلی در سه دسته «ناهنجاری‌های نقطه‌ای» (Point anomalies)، «ناهنجاری‌های زمینه‌ای» (Contextual anomalies) و «ناهنجاری‌های تجمعی» (Collective anomalies) قرار داد. در ادامه هر یک از این موارد به طور خلاصه بیان شده‌اند.

فیلم آموزش تشخیص داده های پرت یا Outlier Detection – رایگان در فرادرس

کلیک کنید

ناهنجاری‌های نقطه‌ای: اگر یک نمونه داده از اکثریت داده‌ها فاصله زیادی داشته باشد، ناهنجاری نقطه‌ای محسوب می‌شود. برای مثال در کارت‌های اعتباری می‌توان از ناهنجاری نقطه‌ای برای تشخیص برداشت‌های عجیب و احتمالا مجرمانه استفاده کرد. در واقع، اگر اغلب برداشت‌های دارنده کارت در طیف مشخصی باشد و یک برداشت با تفاوت مبلغ بسیار زیاد (نسبت به سایر برداشت‌ها) انجام شود، به آن ناهنجاری نقطه‌ای گفته می‌شود.

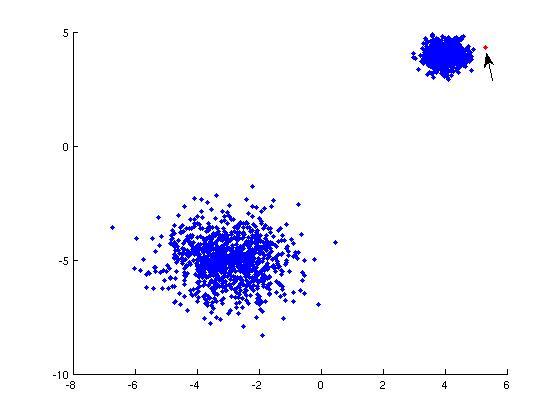
ناهنجاری نقطه‌ای

ناهنجاری زمینه‌ای: چنین ناهنجاری‌هایی وابسته به زمینه‌ای هستند که داده‌کاوی و تشخیص ناهنجاری در آن انجام می‌شود. وقوع چنین ناهنجاری‌هایی در داده‌های سری زمانی متداول است. برای مثال دمای هوای منفی بیست درجه (۲۰-) ممکن است در فصل زمستان کاملا طبیعی باشد اما همین دما در فصل تابستان ناهنجاری در نظر گرفته می‌شود. به عنوان مثالی دیگر باید گفت که پرداخت روزانه بالغ بر ۳۰۰ هزار تومان هزینه ناهار در تعطیلات نوروزی ممکن است امری طبیعی باشد اما پرداخت روزانه این مبلغ برای ناهار در دیگر زمان‌های سال می‌تواند ناهنجاری زمینه‌ای محسوب شود.

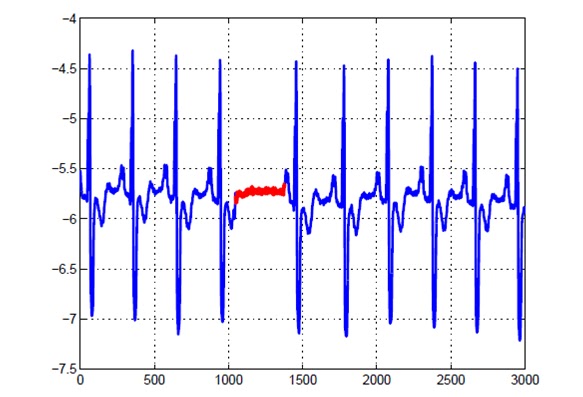
ناهنجاری تجمعی: یک مجموعه از نمونه داده‌های دارای تجمع به شناسایی ناهنجاری‌ها کمک می‌کند. برای مثال، فعالیت شخصی که تلاش می‌کند داده‌ها را از یک ماشین دور به کامپیوتر خود منتقل کند ناهنجاری محسوب می‌شود. مثال بهتری از ناهنجاری تجمعی، نوار قلب انسان است. وجود مقادیر پایین در نوار قلب به خودی خود ناهنجاری نیست، اما هنگامی که تعداد زیادی از این مقادیر پایین به صورت تجمعی اتفاق می‌افتند ناهنجاری در نظر گرفته می‌شوند.

ناهنجاری تجمعی

تشخیص ناهنجاری بسیار شبیه به «حذف نویز» (Noise removal) و تشخیص الگوهای نوظهور است اما با این دو تفاوت دارد. در تشخیص الگوهای نوظهور به شناسایی الگوهایی پیش‌تر مشاهده نشده پرداخته می‌شود. به عنوان مثالی از این امر، می‌توان به علاقه شدید کاربران به یک کانال یوتیوب در طول کریسمس اشاره کرد. حذف نویز، فرآیند ایمن‌سازی تحلیل‌ها از مشاهدات ناخواسته محسوب می‌شود. مثالی از این مورد، حذف نویز از یک سیگنال دارای معنا است.

روش‌های تشخیص ناهنجاری

ساده‌ترین رویکرد برای تشخیص بی‌قاعدگی‌ها در مجموعه داده، پرچم‌گذاری نقاط داده‌ای است که از مشخصه‌های آماری متداول یک توزیع مانند میانگین، میانه، مُد و چارک‌ها فاصله دارند. در واقع می‌توان در تعریف نقطه داده ناهنجار گفت نمونه داده‌ای که با انحراف معیار مشخصی از میانه فاصله داشته باشد، ناهنجار محسوب می‌شود. استفاده از میانه در داده‌های سری زمانی (به دلیل ایستا بودن آن) نمی تواند گزینه خوبی جهت تشخیص ناهنجاری باشد.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

بنابراین به یک پنجره غلتان (متحرک) برای محاسبه میانگین در میان نقاط داده نیاز است. به این روش میانگین متحرک گفته می‌شود و در آن گرایش به روان‌سازی نوسانات کوتاه مدت و برجسته کردن مقادیر دراز مدت وجود دارد. به بیان ریاضی، یک میانگین متحرک ساده n-دوره‌ای را می‌توان به عنوان «فیلتر پایین‌گذر» (low pass filter) نیز در نظر گرفت. فیلتر Kalman نسخه پیچیده‌تری از همین سنجه محسوب می‌شود.

چالش‌ها

فیلترهای پایین‌گذر امکان شناسایی ناهنجاری‌ها در مثال‌های ساده را می‌دهند، اما موقعیت‌هایی نیز وجود دارد که این روش در آن‌ها کار نمی‌کند. برخی از این موارد در ادامه بیان شده‌اند.

داده‌های حاوی نویز ممکن است دارای رفتاری مشابهی با نمونه‌های ناهنجار باشند، زیرا مرزهای بین رفتار بهنجار و ناهنجار معمولا دقیق نیست.
تعریف بهنجار و ناهنجار ممکن است مکررا تغییر کنند. ناهنجاری‌های مخرب به طور مداوم خود را با داده‌های بهنجار تطبیق می‌دهند. بنابراین تعیین آستانه بر اساس میانگین متحرک نمی‌تواند همیشه گزینه مناسبی باشد.
برای الگوهایی که فصل محور هستند، انجام این کار شامل روش‌های پیچیده‌تری مانند تجزیه داده‌ها به گرایش‌های گوناگون به منظور شناسایی تغییرات موجود در فصل‌ها است.

رویکردهای مبتنی بر یادگیری ماشین

در ادامه خلاصه‌ای از روش‌های تشخیص ناهنجاری برپایه یادگیری ماشین ارائه می‌شود.

فیلم آموزش انتخاب مدل های یادگیری ماشین در پایتون Python در فرادرس

کلیک کنید

تشخیص ناهنجاری مبتنی بر چگالی

روش تشخیص ناهنجاری مبتنی بر چگالی برپایه الگوریتم k-نزدیک‌ترین همسایگی است.

فرض: نقاط داده طبیعی در نزدیکی همسایگی‌های چگال و ناهنجاری‌ها بسیار دورتر از آن‌ها هستند.

نزدیک‌ترین مجموعه از نقاط داده به وسیله یک امتیاز ارزیابی می‌شود. این امتیاز می‌تواند فاصله اقلیدسی یا سنجه مشابهی متناسب با نوع داده‌ها باشد (داده دسته‌ای یا عددی است). روش‌های تشخیص ناهنجاری مبتنی بر چگالی را می‌توان به طور کلی در دو دسته قرار داد.

K-نزدیک‌ترین همسایگی: KNN یک روش یادگیری ساده، غیر پارامتری و تنبل است که برای دسته‌بندی داده‌ها براساس مشابهت‌های موجود در متریک‌های فاصله مانند اقلیدسی (Eucledian)، منهتن (Manhattan)، مینکوفسکی (Minkowski) یا همینگ (Hamming) عمل می‌کند.

تراکم نسبی داده‌ها: این روش بیشتر با عنوان «فاکتور دورافتادگی محلی» شناخته می‌شود. این مفهوم بر اساس سنجه فاصله‌ای که به آن «فاصله دسترسی‌پذیری» (eachability distance) گفته می‌شود بنا نهاده شده است.

روش‌های تشخیص ناهنجاری مبتنی بر خوشه‌بندی

خوشه‌بندی یکی از متداول‌ترین مفاهیم در یادگیری نظارت نشده است.

فرض: نقاط داده مشابه گرایش به تعلق به گروه‌ها یا خوشه‌های مشابهی دارند که براساس فاصله آن‌ها از «مرکزوارها» (centroid) تعیین می‌شوند.

K-میانه، الگوریتم خوشه‌بندی است که به طور گسترده در مسائل مختلف داده‌کاوی و تشخیص ناهنجاری مورد استفاده قرار می‌گیرد. این روش، K خوشه مشابه از نقاط داده می‌سازد. نقاط داده‌ای که خارج از این گروه‌ها قرار گیرند پتانسیل آن را دارند که به عنوان ناهنجار برچسب‌گذاری شوند.

روش‌های مبتنی بر ماشین بردار پشتیبان

ماشین بردار پشتیبان دیگر روش موثر برای تشخیص ناهنجاری است. SVM معمولا با یادگیری نظارت شده مرتبط است اما افزونه‌ای مانند OneClassCVM نیز دارد که برای شناسایی ناهنجاری‌ها به عنوان یک مساله نظارت نشده (که در آن داده‌های آموزش برچسب‌گذاری نشده‌اند) قابل استفاده است. الگوریتم، مرزهای نرم را برای خوشه‌بندی نمونه داده‌های بهنجار با استفاده از مجموعه آموزش می‌آموزد و سپس با بهره‌گیری از نمونه‌های تست خود را برای شناسایی ناهنجاری‌هایی که خارج از ناحیه آموخته شده قرار دارند تنظیم می‌کند. بسته به مساله، خروجی یک تشخیص دهنده ناهنجاری می‌تواند یک مقدار اسکالر برای فیلتر کردن آستانه مبتنی بر دامنه یا برچسب‌های متنی (مانند برچسب‌های دودویی/چندگانه) باشد.

ساخت یک تشخیص دهنده ناهنجاری ساده با استفاده از فیلتر پایین گذر

در این بخش بر ساخت یک بسته تشخیص ناهنجاری با استفاده از میانگین متحرک برای شناسایی ناهنجاری‌ها در تعدادی از لکه‌های خورشیدی طی چندین ماه در یک مجموعه داده نمونه تمرکز شده است.

فیلم آموزش کشف داده های پرت در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

این مجموعه داده را می‌توان از این مسیر و با استفاده از دستور زیر دانلود کرد (wget برنامه‌ای رایانه‌ای برای دریافت محتوا از وب است. این نرم‌افزار بخشی از پروژه گنو محسوب می‌شود).

1wget -c -b http://www-personal.umich.edu/~mejn/cp/data/sunspots.txt

این مجموعه داده دارای ۳۱۴۳ سطر است که شامل اطلاعاتی پیرامون لکه‌های خورشیدی گردآوری شده در طول سال‌های ۱۷۴۹ تا ۱۹۸۴ می‌شود. لکه‌های خورشیدی به عنوان نقاط تیره‌ای روی خورشید تعریف می‌شوند. مطالعه لکه‌های خورشیدی به دانشمندان کمک می‌کند که مشخصه‌های خورشید را در دوره‌ای از زمان درک کنند. به طور کلی، لکه خورشیدی یک مشخصه مغناطیسی محسوب می‌شود.

میانگین متحرک با استفاده از همگشت خطی گسسته

«همگشت» (Convolution ) یک عملیات ریاضی است که روی دو تابع برای تولید سومین تابع انجام می‌شود. به بیان ریاضی، همگشت را می‌توان به عنوان انتگرال حاصل‌ضرب دو تابع پس از آنکه یکی از توابع معکوس و شیفت شد، تعریف کرد. فرمول مربوط به این عملیات در ادامه ارائه شده است.

$f*g(t)$ = $\int_{-\infty}^{\infty} f(T)*g(t-T) dT$ که در آن (f(T یک تابع ورودی شامل کمیت quantity of interest است (برای مثال لکه‌های خورشیدی در زمان T محاسبه می‌شوند). (g(t —T یک تابع وزن‌دهی است که بر اساس مقدار t شیفت پیدا می‌کند. بدین شکل، با تغییر T، وزن‌های گوناگون به تابع ورودی (f(T تخصیص داده می‌شود. در بررسی موردی این مطلب، (f(T تعداد لکه‌های خورشیدی در زمان T را ارائه می‌کند. (g(t —T کرنل میانگین متحرک است.

1from __future__ import division
2from itertools import izip, count
3import matplotlib.pyplot as plt
4from numpy import linspace, loadtxt, ones, convolve
5import numpy as np
6import pandas as pd
7import collections
8from random import randint
9from matplotlib import style
10style.use('fivethirtyeight')
11%matplotlib inline

1# 1. Download sunspot dataset and upload the same to dataset directory
2#    Load the sunspot dataset as an Array
3!mkdir -p dataset
4!wget -c -b http://www-personal.umich.edu/~mejn/cp/data/sunspots.txt -P dataset
5data = loadtxt("dataset/sunspots.txt", float)
6
7# 2. View the data as a table
8data_as_frame = pd.DataFrame(data, columns=['Months', 'SunSpots'])
9data_as_frame.head(
10)

SunSpots	Months
۵۸.۰	۰.۰	۰
۶۲.۶	۱.۰	۱
۷۰.۰	۲.۰	۲
۵۵.۷	۳.۰	۳
۸۵.۰	۴.۰	۴

1# 3. Lets define some use-case specific UDF(User Defined Functions)
2
3def moving_average(data, window_size):
4    """ Computes moving average using discrete linear convolution of two one dimensional sequences.
5    Args:
6    -----
7            data (pandas.Series): independent variable
8            window_size (int): rolling window size
9
10    Returns:
11    --------
12            ndarray of linear convolution
13
14    References:
15    ------------
16    [1] Wikipedia, "Convolution", http://en.wikipedia.org/wiki/Convolution.
17    [2] API Reference: https://docs.scipy.org/doc/numpy/reference/generated/numpy.convolve.html
18
19    """
20    window = np.ones(int(window_size))/float(window_size)
21    return np.convolve(data, window, 'same')
22
23
24def explain_anomalies(y, window_size, sigma=1.0):
25  """ Helps in exploring the anamolies using stationary standard deviation
26    Args:
27    -----
28        y (pandas.Series): independent variable
29        window_size (int): rolling window size
30        sigma (int): value for standard deviation
31
32    Returns:
33    --------
34        a dict (dict of 'standard_deviation': int, 'anomalies_dict': (index: value))
35        containing information about the points indentified as anomalies
36
37    """
38    avg = moving_average(y, window_size).tolist()
39    residual = y - avg
40    # Calculate the variation in the distribution of the residual
41    std = np.std(residual)
42    return {'standard_deviation': round(std, 3),
43            'anomalies_dict': collections.OrderedDict([(index, y_i) for
44                                                       index, y_i, avg_i in izip(count(), y, avg)
45              if (y_i > avg_i + (sigma*std)) | (y_i < avg_i - (sigma*std))])}
46
47
48def explain_anomalies_rolling_std(y, window_size, sigma=1.0):
49    """ Helps in exploring the anamolies using rolling standard deviation
50    Args:
51    -----
52        y (pandas.Series): independent variable
53        window_size (int): rolling window size
54        sigma (int): value for standard deviation
55
56    Returns:
57    --------
58        a dict (dict of 'standard_deviation': int, 'anomalies_dict': (index: value))
59        containing information about the points indentified as anomalies
60    """
61    avg = moving_average(y, window_size)
62    avg_list = avg.tolist()
63    residual = y - avg
64    # Calculate the variation in the distribution of the residual
65    testing_std = pd.rolling_std(residual, window_size)
66    testing_std_as_df = pd.DataFrame(testing_std)
67    rolling_std = testing_std_as_df.replace(np.nan,
68                                  testing_std_as_df.ix[window_size - 1]).round(3).iloc[:,0].tolist()
69    std = np.std(residual)
70    return {'stationary standard_deviation': round(std, 3),
71            'anomalies_dict': collections.OrderedDict([(index, y_i)
72                                                       for index, y_i, avg_i, rs_i in izip(count(),
73                                                                                           y, avg_list, rolling_std)
74              if (y_i > avg_i + (sigma * rs_i)) | (y_i < avg_i - (sigma * rs_i))])}
75
76
77# This function is repsonsible for displaying how the function performs on the given dataset.
78def plot_results(x, y, window_size, sigma_value=1,
79                 text_xlabel="X Axis", text_ylabel="Y Axis", applying_rolling_std=False):
80    """ Helps in generating the plot and flagging the anamolies.
81        Supports both moving and stationary standard deviation. Use the 'applying_rolling_std' to switch
82        between the two.
83    Args:
84    -----
85        x (pandas.Series): dependent variable
86        y (pandas.Series): independent variable
87        window_size (int): rolling window size
88        sigma_value (int): value for standard deviation
89        text_xlabel (str): label for annotating the X Axis
90        text_ylabel (str): label for annotatin the Y Axis
91        applying_rolling_std (boolean): True/False for using rolling vs stationary standard deviation
92    """
93    plt.figure(figsize=(15, 8))
94    plt.plot(x, y, "k.")
95    y_av = moving_average(y, window_size)
96    plt.plot(x, y_av, color='green')
97    plt.xlim(0, 1000)
98    plt.xlabel(text_xlabel)
99    plt.ylabel(text_ylabel)
100
101    # Query for the anomalies and plot the same
102    events = {}
103    if applying_rolling_std:
104        events = explain_anomalies_rolling_std(y, window_size=window_size, sigma=sigma_value)
105    else:
106        events = explain_anomalies(y, window_size=window_size, sigma=sigma_value)
107
108    x_anomaly = np.fromiter(events['anomalies_dict'].iterkeys(), dtype=int, count=len(events['anomalies_dict']))
109    y_anomaly = np.fromiter(events['anomalies_dict'].itervalues(), dtype=float,
110                                            count=len(events['anomalies_dict']))
111    plt.plot(x_anomaly, y_anomaly, "r*", markersize=12)
112
113    # add grid and lines and enable the plot
114    plt.grid(True)
115    plt.show()

1# 4. Lets play with the functions
2x = data_as_frame['Months']
3Y = data_as_frame['SunSpots']
4
5# plot the results
6plot_results(x, y=Y, window_size=10, text_xlabel="Months", sigma_value=3,
7             text_ylabel="No. of Sun spots")
8events = explain_anomalies(y, window_size=5, sigma=3)
9
10# Display the anomaly dict
11print("Information about the anomalies model:{}".format(events))

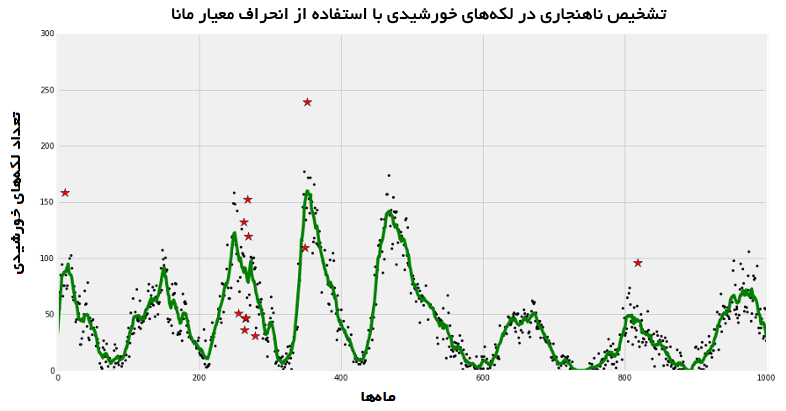
تشخیص ناهنجاری

در ادامه این مساله مورد بررسی قرار می‌گیرد که آیا تابع تشخیص ناهنجاری ارائه شده در بالا را می‌توان برای دیگر بررسی‌های موردی استفاده کرد یا خیر. فرض می‌شود که یک مجموعه داده تصادفی متعلق به ارزش گذاری سهام شرکت A در طول زمان است. محور X زمان (روزها) و محور y مقدار سهام را به دلار نشان می‌دهد.

1# Convenience function to add noise
2def noise(yval):
3    """ Helper function to generate random points """
4    np.random.seed(0)
5    return 0.2*np.asarray(yval)*np.random.normal(size=len(yval))
6
7# Generate a random dataset
8def generate_random_dataset(size_of_array=1000, random_state=0):
9    """ Helps in generating a random dataset which has a normal distribution
10    Args:
11    -----
12        size_of_array (int): number of data points
13        random_state (int): to initialize a random state
14
15    Returns:
16    --------
17        a list of data points for dependent variable, pandas.Series of independent variable
18    """
19    np.random.seed(random_state)
20    y = np.random.normal(0, 0.5, size_of_array)
21    x = range(0, size_of_array)
22    y_new = [y_i + index**((size_of_array - index)/size_of_array) +  noise()
23     for index, y_i in izip(count(), y)]
24    return x, pd.Series(y_new)
25
26
27# Lets play
28x1, y1 = generate_random_dataset()
29# Using stationary standard deviation over a continuous sample replicating
30plot_results(x1, y1, window_size=12, title_for_plot="Statinoary Standard Deviation",
31                    sigma_value=2, text_xlabel="Time in Days", text_ylabel="Value in $")
32
33# using rolling standard deviation for
34x1, y1 = generate_random_dataset()
35plot_results(x1, y1, window_size=50, title_for_plot="Using rolling standard deviation",
36             sigma_value=2, text_xlabel="Time in Days", text_ylabel="Value in $", applying_rolling_std=True)

تشخیص ناهنجاری

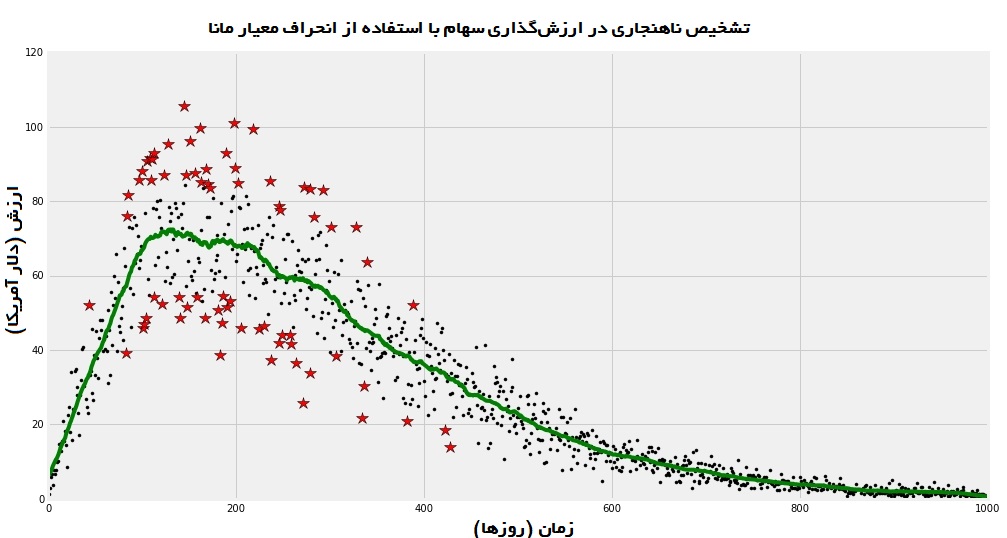
به نظر می‌رسد که تشخیص دهنده ناهنجاری معرفی شده عملکرد خوبی دارد. این تشخیص دهنده قادر به شناسایی نقاط داده‌ای که دو سیگما از منحنی برازش شده فاصله دارند است. بسته به توزیع داده‌های یک مساله، در تنظیمات سری زمانی و پویایی محیط ممکن است نیاز به استفاده از انحراف معیار مانا (سراسری) یا غیر مانا (محلی) برای تثبیت یک مدل باشد. تابع ریاضی حول محور انحراف معیار را می‌توان به سادگی برای استفاده از فرمول‌سازی سفارشی ویرایش کرد.

تذکر: روش ارائه شده در بالا صرفا برای نشان دادن مفاهیم تشخیص ناهنجاری است و بهینه‌ترین راهکارهای موجود برای این کار محسوب نمی‌شود.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر نوشته بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۹ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

Data Science ویکی‌پدیای انگلیسی

الهام حصارکی (+)

«الهام حصارکی»، فارغ‌التحصیل مقطع کارشناسی ارشد مهندسی فناوری اطلاعات، گرایش سیستم‌های اطلاعات مدیریت است. او در زمینه هوش مصنوعی و داده‌کاوی، به ویژه تحلیل شبکه‌های اجتماعی، فعالیت می‌کند.