چندضلعی ها در هندسه – به زبان ساده
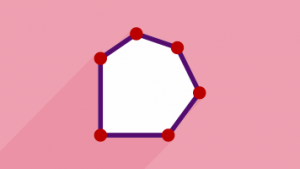
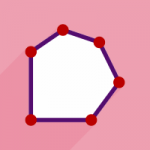
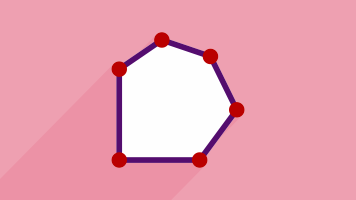
در این پست قصد داریم با ذکر چندین مثال به معرفی انواع چندضلعی و ویژگیهایشان بپردازیم. در ابتدای راه و پیش از شروع کار بهتر است تعریفی درباره چندضلعیها ارائه دهیم. در علم هندسه و ریاضیات، هر شکل دوبعدی و بسته را که دارای سه ضلع یا تعداد اضلاع بیشتری باشد چندضلعی (Polygon) مینامند.
در دنیای ریاضیات، اشکال هندسی را برحسب زوایا و موقعیت اضلاع نسبت به یکدیگر در چندین گروه دستهبندی میکنند. در ادامه به معرفی هریک از این دستهبندیها خواهیم پرداخت.
انواع چندضلعیها
منتظم: هرگاه در یک هندسه تمامی اضلاع و زوایای داخلی با یکدیگر برابر باشند چندضلعی موردنظر در دسته اشکال منتظم قرار می گیرد.
نامنتظم: درصورتی که در هندسه موردنظرمان تمامی اضلاع و زوایای داخلی با یکدیگر برابر نباشند (در دسته بالا قرار نگیرد)، چندضلعی موردنظر در دسته اشکال نامنتظم قرار می گیرد.
نمونه ای از چندضلعیهای منتظم:

نمونه ای از چندضلعیهای نامنتظم:

مقعر: هرگاه در یک هندسه حداقل یکی از زوایای داخلی اندازهای بیشتر از 180 درجه داشته باشد، چندضلعی موردنظر در دسته اشکال هندسی مقعر قرار می گیرد.
محدب: در صورتی که یک هندسه، زوایای داخلی با اندازهای کمتر از 180 درجه داشته باشد(در دسته بالا قرار نگیرد)، چندضلعی موردنظر در دسته اشکال هندسی محدب قرار می گیرد.
نمونه ای از چندضلعیهای مقعر:

نمونه ای از چندضلعیهای محدب:

پیچیده: هرگاه در یک هندسه حداقل یکی از اضلاع از روی ضلع دیگری عبور کرده باشد، چندضلعی موردنظر در دسته اشکال هندسی پیچیده قرار میگیرد.
ساده: هرگاه در یک هندسه هیچ یک از اضلاع از روی ضلع دیگری عبور نکرده باشد (در دسته بالا قرار نگیرد)، چندضلعی موردنظر در دسته اشکال هندسی ساده قرار میگیرد.
نمونه ای از چندضلعیهای پیچیده:

نمونه ای از چندضلعیهای ساده:

اگر تمایل به مطالعه بیشتر در مورد این موضوعات را داشته باشید؛ شاید آموزش های زیر نیز برای شما مفید باشند:
- سطح مقطع در هندسه — به زبان ساده
- تعریف حلقه و محاسبات آن در هندسه — به زبان ساده
- حرکت انتقالی در ریاضیات — به زبان ساده
- تقارن چرخشی در اشکال دوبعدی — به زبان ساده
#











