حمله تخاصمی (Adversarial Attack) با مدل FGSM در پایتون — راهنمای کاربردی

بسیاری از افرادی که در حوزه «یادگیری ماشین» (Machine Learning | ML) فعالیت و پژوهش میکنند به خوبی آگاه هستند که برخی از مدلهای یادگیری ماشین چقدر عملکرد تاثیرگذاری دارند. پژوهشهایی که در این حوزه انجام میشود موجب شده تا مدلها سریعتر، صحیحتر و موثرتر از قبل بشوند. اگرچه، جنبهای از طراحی و آموزش مدل که اغلب نادیده گرفته میشود امنیت و استحکام مدل است. این موضوع به طور خاص هنگامی اهمیت پیدا میکند که یک متخاصم سعی در گول زدن مدل داشته باشد. این مساله ممکن است بسیاری از افراد را حیرت زده کند که اضافه کردن برخی اختلالات (آشفتگیهای) نامحسوس در تصاویر، میتواند کارایی مدل را به شدت متفاوت کند. با در نظر گرفتن این موضوع، در این راهنما مثالی پیرامون یک دستهبند متنی ارائه خواهد شد. در این مطلب، به طور خاص از یکی از اولین و متداولترین نوع حملات با عنوان «حمله علامت گرادیان سریع» (Fast Gradient Sign Attack | FCSA) برای گول زدن یک «دستهبند» (Classifier) از نوع MNIST استفاده خواهد شد. با مطالعه این راهنما و کسب شناخت از حمله تخاصمی (Adversarial Attack) با مدل FGSM در پایتون، آگاهی مخاطبان پیرامون آسیبپذیریهای امنیتی مدلهای یادگیری ماشین افزایش پیدا میکند و بینشی پیرامون یادگیری ماشین تخاصمی به دست میآورند.
مدل مخرب
دستههای گوناگونی از حملات تخاصمی وجود دارند. هر یک از این حملات دارای هدف و فرضی متفاوت بر اساس دانش مهاجم هستند. اگرچه، به طور کلی هدف کلاهبرداری اضافه کردن مقداری انحراف (آشفتگی) به دادههای ورودی به منظور انجام دستهبندی غلط توسط مدل روی آنها است. چندین نوع از فرضیات از دانش مهاجم پیرامون مدل وجود دارد که دو مورد از آنها «جعبه سفید» (white-box) و «جعبه سیاه» (black-box) هستند. یک حمله جعبه سفید فرض میکند که مهاجم دارای دانش و دسترسی کامل به مدل شامل معماری، ورودیها، خروجیها و وزنهای آن است.
در یک حمله جعبه سیاه، فرض بر این است که حمله کننده تنها دارای دسترسی به ورودیها و خروجیهای مدل است و هیچ چیز درباره معماری یا وزنهای مدل نمیداند. همچنین، انواع گوناگونی از اهداف نیز وجود دارد که از این جمله میتوان به دستهبندی غلط و دستهبندی غلط منبع/هدف اشاره کرد. در دستهبندی غلط هدف متخاصم فقط این است که دستهبندی خروجی غلط باشد، اما اهمیتی نمیدهد که دستهبندی جدید چیست. دستهبندی منبع/هدف، بدین معنا است که متخاصم میخواهد یک تصویر که در اصل از یک کلاس منبع خاص است را در یک کلاس هدف خاص (اشتباه) دستهبندی کند. در مثال ارائه شده در این مطلب، حمله FGSM که یک حمله جعبه سفید است و هدف دستهبندی غلط انجام میشود، پیادهسازی شده است. با این اطلاعات پیشزمینهای، اکنون میتوان پیرامون جزئیات حمله بحث کرد.
حمله علامت گرادیان سریع
یکی از محبوبترین نوع حملات تخاصمی تا به امروز «Fast Gradient Sign Attack | FGSM» است و توسط «ایان گودفِلو» (Ian Goodfellow) و همکاران در مقالهای با عنوان «تشریح و بهرهبرداری از مثالهای تخاصمی» (Explaining and Harnessing Adversarial Examples) ارائه شده است. این حمله به طور قابل توجهی قدرتمند و نوآورانه است. FGSM برای حمله به شبکههای عصبی با نفوذ به روش یادگیری آنها یعنی «گرادیان» (Gradients) طراحی شده است.
ایده این کار ساده است و به جای کار برای کمینه کردن «زیان» (Loss) با تنظیم وزنها بر پایه «گرادیان بازگشت به عقب» (backpropagated gradients)، حمله دادههای ورودی را با هدف بیشینهسازی زیان برپایه بازگشت به عقب مشابهی تنظیم میکند. به عبارت دیگر، حمله از گرادیان زیان w.r.t داده ورودی استفاده و سپس داده ورودی را برای بیشینه کردن زیان تنظیم میکند. پیش از آنکه کد لازم برای این کار ارائه شود، نگاهی به مثال معروف پاندا FGSM انداخته و نکاتی پیرامون آن بیان میشود.

با توجه به تصویر بالا، x تصویر ورودی اصلی است که به درستی به عنوان «Panda» شناسایی میشود، y برچسب حقیقت زمینهای برای x محسوب میشود و θ پارامترهای مدل را نشان میدهد. (J(θ,x,y هزینهای است که برای آموزش دادن شبکه مورد استفاده قرار میگیرد. حمله به منظور محاسبه (xJ(θ,x,y∇، گرادیان را بازگشت به عقب به دادههای ورودی میدهد. سپس، دادههای ورودی را با یک گام کوچک (ϵ یا 0.007 در تصویر) در جهتی که ((sign(∇xJ(θ,x,y) زیان را بیشینه میسازد تنظیم میکند. تصویر آaفته حاصل شده ′x است که توسط شبکه هدف به اشتباه به عنوان «میمون دراز دست» (gibbon) دستهبندی شده، در حالی که میتوان به وضوح دید که یک پاندا است. خوشبختانه اکنون دیگر مفاهیم نهفته در پس این راهنما واضح است، بنابراین میتوان مستقیم به سراغ پیادهسازی رفت.
1from __future__ import print_function
2import torch
3import torch.nn as nn
4import torch.nn.functional as F
5import torch.optim as optim
6from torchvision import datasets, transforms
7import numpy as np
8import matplotlib.pyplot as pltپیادهسازی حمله تخاصمی (Adversarial Attack) با مدل FGSM
در این بخش، به پارامترهای ورودی پرداخته خواهد شد و سپس حمله با پایتون پیادهسازی و آزمونهایی اجرا میشود.
ورودیها
تنها سه ورودی برای این روش وجود دارد که به صورت زیر تعریف شدهاند:
اپسیلونها (epsilons): لیست مقادیر اپسیلون برای استفاده در اجرا است. اهمیت دارد که ۰ را در لیست نگاه داشت زیرا نشانگر کارایی مدل در مجموعه تست اصلی است. همچنین، به طور مستقیم انتظار اپسیلون بزرگتر و آشفتگیهای قابل توجهتری میرود، اما در عین حال انتظار میرود که حملات موثرتری باشند که بیشتر بتوانند صحت مدل را کاهش دهند. از آنجا که طیف دادهها در اینجا [0,1] است، هیچ مقدار اپسیلونی نباید از یک تجاوز کند.
pretrained_model: مسیری به مدل MNIST از پیشآموزش داده شده با pytorch/examples/mnist است. برای سادگی، میتوان مدل از پیش آموزش داده شده را از اینجا (+) دانلود کرد.
use_cuda: «پرچم دودویی» (boolean flag) برای استفاد از CUDA در صورت تمایل و در دسترس بودن است. شایان توجه است که GPU با CUDA در این راهنما امری الزامی نیست، زیرا CPU هم زمان اجرای زیادی ندارد.
1epsilons = [0, .05, .1, .15, .2, .25, .3]
2pretrained_model = "data/lenet_mnist_model.pth"
3use_cuda=Trueمدل زیر حمله
همانطور که پیشتر بیان شد، مدل تحت حمله مشابه مدل MNIST موجود در pytorch/examples/mnist است. کاربر ممکن است مدل MNIST خودش را آموزش بدهد و ذخیره کند یا میتواند مدل آماده شده موجود را دانلود و استفاده کند. تعریف Net و «بارگذار داده آزمون» (test dataloader) در اینجا از مثال MNIST کپی شدهاند.
هدف این بخش تعریف مدل و بارگذار داده و سپس مقداردهی اولیه مدل و بارگذاری وزنهای از پیش تعریف شده است.
1# LeNet Model definition
2class Net(nn.Module):
3 def __init__(self):
4 super(Net, self).__init__()
5 self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
6 self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
7 self.conv2_drop = nn.Dropout2d()
8 self.fc1 = nn.Linear(320, 50)
9 self.fc2 = nn.Linear(50, 10)
10
11 def forward(self, x):
12 x = F.relu(F.max_pool2d(self.conv1(x), 2))
13 x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
14 x = x.view(-1, 320)
15 x = F.relu(self.fc1(x))
16 x = F.dropout(x, training=self.training)
17 x = self.fc2(x)
18 return F.log_softmax(x, dim=1)
19
20# MNIST Test dataset and dataloader declaration
21test_loader = torch.utils.data.DataLoader(
22 datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
23 transforms.ToTensor(),
24 ])),
25 batch_size=1, shuffle=True)
26
27# Define what device we are using
28print("CUDA Available: ",torch.cuda.is_available())
29device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")
30
31# Initialize the network
32model = Net().to(device)
33
34# Load the pretrained model
35model.load_state_dict(torch.load(pretrained_model, map_location='cpu'))
36
37# Set the model in evaluation mode. In this case this is for the Dropout layers
38model.eval()خروجی:
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ../data/MNIST/raw/train-images-idx3-ubyte.gz Extracting ../data/MNIST/raw/train-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ../data/MNIST/raw/train-labels-idx1-ubyte.gz Extracting ../data/MNIST/raw/train-labels-idx1-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ../data/MNIST/raw/t10k-images-idx3-ubyte.gz Extracting ../data/MNIST/raw/t10k-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ../data/MNIST/raw/t10k-labels-idx1-ubyte.gz Extracting ../data/MNIST/raw/t10k-labels-idx1-ubyte.gz Processing... Done! CUDA Available: True
حمله FGSM
اکنون، میتوان تابعی که مثالهای تخاصمی را با آشفته کردن دادههای اصلی میسازد تعریف کرد. تابع fgsm_attack سه ورودی را دریافت میکند. image همان تصویر سالم (x)، ورودی epsilon مقدار آشفتگی متناسب با پیکسل (ϵ)، و data_grad گرادیان زیان از زیان w.r.t تصویر ورودی ((xJ(θ,x,y∇) است. تابع در ادامه تصویر منحرف شده را به صورت زیر میسازد:
((perturbed_image=image+epsilon∗sign(data_grad)=x+ϵ∗sign(∇xJ(θ,x,y
در نهایت، به منظور نگهداری طیف اصلی دادهها، تصویر منحرف شده در دامنه [0,1] محدود شده است.
1# FGSM attack code
2def fgsm_attack(image, epsilon, data_grad):
3 # Collect the element-wise sign of the data gradient
4 sign_data_grad = data_grad.sign()
5 # Create the perturbed image by adjusting each pixel of the input image
6 perturbed_image = image + epsilon*sign_data_grad
7 # Adding clipping to maintain [0,1] range
8 perturbed_image = torch.clamp(perturbed_image, 0, 1)
9 # Return the perturbed image
10 return perturbed_imageتابع تست
در نهایت، نتیجه مرکزی این راهنما از تابع test میآید. هر فراخوانی این تابع تست یک گام تست کامل را در مجموعه تست MNIST اجرا میکند و صحت نهایی را گزارش میدهد. اگرچه، شایان توجه است که این تابع نیز یک ورودی epsilon را دریافت میکند. این بدین دلیل به وقوع میپیوندد که تابع test صحت مدلی که تحت حمله متخاصم است را گزارش میکند. به طور مشخصتر باید گفت که برای هر نمونه در مجموعه تست، تابع گرادیان زیان w.r.t داده ورودی (data_grad) را محاسبه میکند، یک تصویر منحرف شده با (fgsm_attack (perturbed_data میسازد و سپس بررسی میکند که آیا مثال آشفته شده تخاصمی است. علاوه بر تست صحت مدل، تابع مثالهای تخاصمی موفقی را برای آنکه بعدا بصریسازی شوند ذخیره میکند و باز میگرداند.
1def test( model, device, test_loader, epsilon ):
2
3 # Accuracy counter
4 correct = 0
5 adv_examples = []
6
7 # Loop over all examples in test set
8 for data, target in test_loader:
9
10 # Send the data and label to the device
11 data, target = data.to(device), target.to(device)
12
13 # Set requires_grad attribute of tensor. Important for Attack
14 data.requires_grad = True
15
16 # Forward pass the data through the model
17 output = model(data)
18 init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
19
20 # If the initial prediction is wrong, dont bother attacking, just move on
21 if init_pred.item() != target.item():
22 continue
23
24 # Calculate the loss
25 loss = F.nll_loss(output, target)
26
27 # Zero all existing gradients
28 model.zero_grad()
29
30 # Calculate gradients of model in backward pass
31 loss.backward()
32
33 # Collect datagrad
34 data_grad = data.grad.data
35
36 # Call FGSM Attack
37 perturbed_data = fgsm_attack(data, epsilon, data_grad)
38
39 # Re-classify the perturbed image
40 output = model(perturbed_data)
41
42 # Check for success
43 final_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
44 if final_pred.item() == target.item():
45 correct += 1
46 # Special case for saving 0 epsilon examples
47 if (epsilon == 0) and (len(adv_examples) < 5):
48 adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
49 adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
50 else:
51 # Save some adv examples for visualization later
52 if len(adv_examples) < 5:
53 adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
54 adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
55
56 # Calculate final accuracy for this epsilon
57 final_acc = correct/float(len(test_loader))
58 print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))
59
60 # Return the accuracy and an adversarial example
61 return final_acc, adv_examplesاجرای حمله
آخرین بخش از پیادهسازی آن است که در واقع حمله اجرا شود. در اینجا، یک گام تست کامل برای هر مقدار اپسیلون در ورودی epsilons اجرا میشود. برای هر اپسیلون، صحت نهایی و برخی از مثالهای تخاصمی موفق برای ترسیم شدن در بخشهای آتی ذخیره میشوند.
شایان توجه است که صحتهای پرینت شده چگونه با افزایش مقدار اپسیلونها، کاهش پیدا میکنند. حالت ϵ=0 که صحت تست اصلی را بدون حمله نشان میدهد نیز جالب توجه است.
1accuracies = []
2examples = []
3
4# Run test for each epsilon
5for eps in epsilons:
6 acc, ex = test(model, device, test_loader, eps)
7 accuracies.append(acc)
8 examples.append(ex)خروجی:
Epsilon: 0 Test Accuracy = 9810 / 10000 = 0.981 Epsilon: 0.05 Test Accuracy = 9426 / 10000 = 0.9426 Epsilon: 0.1 Test Accuracy = 8510 / 10000 = 0.851 Epsilon: 0.15 Test Accuracy = 6826 / 10000 = 0.6826 Epsilon: 0.2 Test Accuracy = 4301 / 10000 = 0.4301 Epsilon: 0.25 Test Accuracy = 2082 / 10000 = 0.2082 Epsilon: 0.3 Test Accuracy = 869 / 10000 = 0.0869
نتایج
اولین نتیجه، نمودار «صحت» (accuracy) در مقایسه با «اپسیلون» (epsilon) است. همانطور که پیشتر اشاره شد، با افزایش اپسیلون، انتظار میرود که صحت مدل کاهش پیدا کند. این امر بدین دلیل است که هرچه اپسیلون بیشتر باشد این معنی را میدهد که گام بزرگتری در جهتی که زیان را بیشینه میکند برداشته شده است.
شایان توجه است که گرایش در این منحنی خطی نیست، حتی هنگامی که مقادیر اپسیلون فاصلهگذاری خطی شدهاند. برای مثال، صحت در ϵ=0.05 تنها حدود ٪۴ کمتر از ϵ=0 است، اما صحت در ϵ=0.2 به میزان ٪۲۵ کمتر از ϵ=0.15 است. همچنین، شایان توجه است که صحت مدل بر صحت تصادفی برای ۱۰ کلاس دستهبند بین ϵ=0.25 و ϵ=0.3 چیره میشود.
1plt.figure(figsize=(5,5))
2plt.plot(epsilons, accuracies, "*-")
3plt.yticks(np.arange(0, 1.1, step=0.1))
4plt.xticks(np.arange(0, .35, step=0.05))
5plt.title("Accuracy vs Epsilon")
6plt.xlabel("Epsilon")
7plt.ylabel("Accuracy")
8plt.show()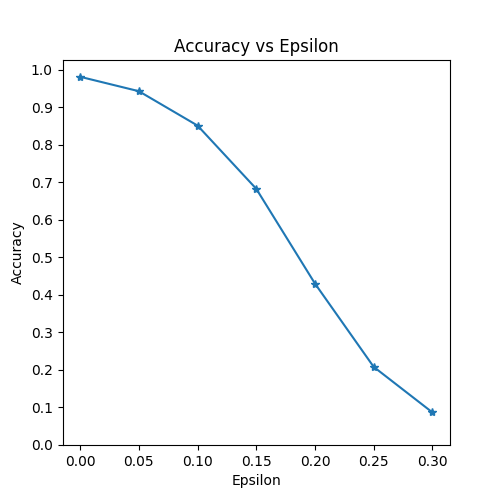
نمونه مثال تخاصمی
با توجه به مفهوم «no free lunch»، در این شرایط، با افزایش اپسیلون، صحت کل کاهش پیدا میکند، اما انحراف راحت تر قابل مشاهده میشود. در واقعیت، موازنهای بین کاهش صحت و آشفتگی وجود دارد که یک مهاجم باید آن را در نظر داشته باشد. در اینجا، مثالهایی از موفقیت نمونههای تخاصمی در هر مقدار اپسیلون ارائه شده است. هر سطر از نمودار یک مقدار اپسیلون متفاوت از خود نشان میدهد.
سطر اول مثالهای ϵ=0 هستند که تصوویر «پاک» اولیه را بدون هرگونه انحراف نشان میدهد. عنوان هر تصویر «original classification -> adversarial classification» را نشان میدهد. شایان توجه است که در همه شرایطها انسانها همچنان قادر به شناسایی دسته صحیح علارغم وجود نویز هستند.
1# Plot several examples of adversarial samples at each epsilon
2cnt = 0
3plt.figure(figsize=(8,10))
4for i in range(len(epsilons)):
5 for j in range(len(examples[i])):
6 cnt += 1
7 plt.subplot(len(epsilons),len(examples[0]),cnt)
8 plt.xticks([], [])
9 plt.yticks([], [])
10 if j == 0:
11 plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
12 orig,adv,ex = examples[i][j]
13 plt.title("{} -> {}".format(orig, adv))
14 plt.imshow(ex, cmap="gray")
15plt.tight_layout()
16plt.show()
کد منبع کامل FGSM در پایتون
1Jupyter Notebook
2fgsm_tutorial.py
3a few seconds ago
4Python
5File
6Edit
7View
8Language
9
10327
11# Results
12328
13# -------
14329
15#
16330
17# Accuracy vs Epsilon
18331
19# ~~~~~~~~~~~~~~~~~~~
20332
21#
22333
23# The first result is the accuracy versus epsilon plot. As alluded to
24334
25# earlier, as epsilon increases we expect the test accuracy to decrease.
26335
27# This is because larger epsilons mean we take a larger step in the
28336
29# direction that will maximize the loss. Notice the trend in the curve is
30337
31# not linear even though the epsilon values are linearly spaced. For
32338
33# example, the accuracy at :math:`\epsilon=0.05` is only about 4% lower
34339
35# than :math:`\epsilon=0`, but the accuracy at :math:`\epsilon=0.2` is 25%
36340
37# lower than :math:`\epsilon=0.15`. Also, notice the accuracy of the model
38341
39# hits random accuracy for a 10-class classifier between
40342
41# :math:`\epsilon=0.25` and :math:`\epsilon=0.3`.
42343
43#
44344
45
46345
47plt.figure(figsize=(5,5))
48346
49plt.plot(epsilons, accuracies, "*-")
50347
51plt.yticks(np.arange(0, 1.1, step=0.1))
52348
53plt.xticks(np.arange(0, .35, step=0.05))
54349
55plt.title("Accuracy vs Epsilon")
56350
57plt.xlabel("Epsilon")
58351
59plt.ylabel("Accuracy")
60352
61plt.show()
62353
63
64354
65
66355
67######################################################################
68356
69# Sample Adversarial Examples
70357
71# ~~~~~~~~~~~~~~~~~~~~~~~~~~~
72358
73#
74359
75# Remember the idea of no free lunch? In this case, as epsilon increases
76360
77# the test accuracy decreases **BUT** the perturbations become more easily
78361
79# perceptible. In reality, there is a tradeoff between accuracy
80362
81# degredation and perceptibility that an attacker must consider. Here, we
82363
83# show some examples of successful adversarial examples at each epsilon
84364
85# value. Each row of the plot shows a different epsilon value. The first
86365
87# row is the :math:`\epsilon=0` examples which represent the original
88366
89# “clean” images with no perturbation. The title of each image shows the
90367
91# “original classification -> adversarial classification.” Notice, the
92368
93# perturbations start to become evident at :math:`\epsilon=0.15` and are
94369
95# quite evident at :math:`\epsilon=0.3`. However, in all cases humans are
96370
97# still capable of identifying the correct class despite the added noise.
98371
99#
100372
101
102373
103# Plot several examples of adversarial samples at each epsilon
104374
105cnt = 0
106375
107plt.figure(figsize=(8,10))
108376
109for i in range(len(epsilons)):
110377
111 for j in range(len(examples[i])):
112378
113 cnt += 1
114379
115 plt.subplot(len(epsilons),len(examples[0]),cnt)
116380
117 plt.xticks([], [])
118381
119 plt.yticks([], [])
120382
121 if j == 0:
122383
123 plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
124384
125 orig,adv,ex = examples[i][j]
126385
127 plt.title("{} -> {}".format(orig, adv))
128386
129 plt.imshow(ex, cmap="gray")
130387
131plt.tight_layout()
132388
133plt.show()
134389
135
136390
137
138391
139######################################################################
140392
141# Where to go next?
142393
143# -----------------
144394
145#
146395
147# Hopefully this tutorial gives some insight into the topic of adversarial
148396
149# machine learning. There are many potential directions to go from here.
150397
151# This attack represents the very beginning of adversarial attack research
152398
153# and since there have been many subsequent ideas for how to attack and
154399
155# defend ML models from an adversary. In fact, at NIPS 2017 there was an
156400
157# adversarial attack and defense competition and many of the methods used
158401
159# in the competition are described in this paper: `Adversarial Attacks and
160402
161# Defences Competition <https://arxiv.org/pdf/1804.00097.pdf>`__. The work
162403
163# on defense also leads into the idea of making machine learning models
164404
165# more *robust* in general, to both naturally perturbed and adversarially
166405
167# crafted inputs.
168406
169#
170407
171# Another direction to go is adversarial attacks and defense in different
172408
173# domains. Adversarial research is not limited to the image domain, check
174409
175# out `this <https://arxiv.org/pdf/1801.01944.pdf>`__ attack on
176410
177# speech-to-text models. But perhaps the best way to learn more about
178411
179# adversarial machine learning is to get your hands dirty. Try to
180412
181# implement a different attack from the NIPS 2017 competition, and see how
182413
183# it differs from FGSM. Then, try to defend the model from your own
184414
185# attacks.
186415
187#
188416
189
190417
191کل زمان اجرای این اسکریپت: ۳ دقیقه و ۷.۳۳۳ ثانیه
گام بعدی
خوشبختانه این راهنما بینش خوبی از یادگیری ماشین تخاصمی فراهم میکند. جهتهای بالقوه زیادی وجود دارند که میتوان در ادامه به سمت آنها رفت. این نوع از حمله، شروعی بسیار مقدماتی برای پژوهشهای حملات تخاصمی است و از سوی دیگر، موضوعی که به آن پرداخته میشود چگونگی مقابله با این حملههای تخاصمی برای دفاع از یک مدل یادگیری ماشین در مقابل یک متخاصم است.
در کنفرانس NIPS 2017 یک رقابت حمله و دفاع برگزار شد و بسیاری از روشهای مورد استفاده در این رقابت در این مقاله (+) معرفی شدهاند. کار روی روشهای دفاع نیز منجر به ایده ساخت مدلهای یادگیری ماشین «مستحکم» (robust) به صورت کلی هم برای آشفتگی طبیعی و هم آشفتگی ناشی از حملات تخاصمی شده است.
دیگر جهتی که میتوان در آن گام برداشت، حملات تخاصمی و دفاع در برابر آنها در دامنههای گوناگون است. پژوهشهای تخاصمی به دامنه تصاویر محدود نشدهاند. برای مثال، این حمله (+) را روی مدلهای گفتار به متن (speech-to-text models) میتوان مشاهده کرد. برای یادگیری بیشتر، میتوان یکی دیگر از مدلهای رقابتهای NIPS 2017 را پیادهسازی و تفاوتهای آن با FGSM را مشاهده کرد. سپس از مدل در مقابل حملات دفاع کرد.
اگر نوشته بالا برای شما مفید بود، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای هوش محاسباتی
- آموزش یادگیری عمیق (Deep learning)
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- فراگیری مفاهیم هوش مصنوعی — مجموعه مقالات جامع وبلاگ فرادرس
- دادهکاوی (Data Mining) — از صفر تا صد
- یادگیری عمیق (Deep Learning) با پایتون — به زبان ساده
^^










