کوانتش ویلسون زومرفلد (Wilson Sommerfeld Quantization) – به زبان ساده
در این مقاله در نظر داریم تا با زبانی ساده به یکی از مهمترین مباحث فیزیک مدرن (جدید) که خود مقدمهای بر آغاز مکانیک کوانتومی پیشرفته است، بپردازیم. با ما در ادامه این مقاله همراه باشید تا با اصل کوانتش ویلسون زومرفلد (Wilson Sommerfeld Quantization Rule) آشنا شوید. قاعده کوانتش ویلسون زومرفلد از این حیث که ذهنیت را از دنیای فیزیک کلاسیک به آرامی وارد دنیای کوانتومی میکند، جهت درک فیزیک و مکانیک کوانتومی از اهمیت زیادی برخوردار است.


قاعدههای کوانتش
در ۳ مقاله «جسم سیاه در فیزیک — به زبان ساده»، «اثر فوتوالکتریک (Photoelectric Effect) — به زبان ساده» و «طیف اتمی — از صفر تا صد» دیدیم عاملی که باعث موفقیت در توجیه پدیدههای تابش جسم سیاه، اثر فوتوالکتریک و ترازهای اتم هیدروژن شد، کوانتیزه یا کوانتیده فرض کردن ترازهای انرژی و تکانه زاویهای به صورت و بود.
در دو رابطه مذکور عدد صحیح مثبت است که از ۰ (برای تابش جسم سیاه) یا ۱ (برای مدل بور) شروع شده و تا بینهایت ادامه مییابد. نیز فرکانس، ثابت پلانک با مقدار و ثابت پلانک کاهش یافته است. در آن زمان درک و چرایی کوانتیزه فرض کردن ترازهای انرژی برای جامعه علمی مبهم بود.
اوایل قرن بیستم در حدود سال 1916 میلادی دو دانشمند به نامهای ویلسون (Wilson) و زومرفلد (Sommerfeld) اصلی را ارائه کردند که هر دو قاعده کوانتش فوق ( و ) را در حالت خاصی در بر میگرفت. اصل یا طرح پیشنهادی آنها تنها برای سیستمهایی که مختصه مکانی آنها متناوب با زمان است به کار میرود.
این اصل وابسته به کوانتیزه کردن متغیر کنش در مکانیک کلاسیکی است. قاعده کوانتش ویلسون زومرفلد به صورت زیر است:
(1)
در رابطه فوق، عدد کوانتومی (گسسته) است که از صفر شروع شده و به صورت واحد افزایش پیدا میکند. متغیر نیز مزدوج تکانه (momentum conjugate) مربوط به مختصه مکانی است. انتگرال بسته فوق روی یک دوره کامل از مختصه مکانی محاسبه میشود. در ادامه این مقاله در نظر داریم تا با استفاده از اصل کوانتش ویلسون زومرفلد، به اصل یا قاعده کوانتش ماکس پلانک () و بوهر () برسیم.

قاعده کوانتش ویلسون زومرفلد و کوانتش پلانک
در این بخش در نظر داریم تا به رابطه کوانتش پلانک از روی رابطه کوانتش ویلسون زومرفلد برسیم. برای این منظور، یک نوسانگر هماهنگ ساده یک بعدی را در نظر بگیرید. در سیستم نوسانگر مذکور، ذرهای به جرم بین دو نقطه نوسان میکند. از مباحث فیزیک کلاسیک به یاد داریم که انرژی مکانیکی (جنبشی + پتانسیل) سیستم مذکور به صورت زیر محاسبه میشود:
(2)
با توجه به رابطه فوق، تکانه که تابعی از انرژی کل و مکان است، به صورت زیر در میآید:
(3)
با توجه به رابطه قاعده کوانتش ویلسون زومرفلد (رابطه ۱)، تکانه ، عبارت فوق و مختصه مکانی که جزء دیفرانسیلی انتگرال را تشکیل میدهد، است. بیان کردیم که انتگرال باید روی یک دوره کامل از مختصه مکانی محاسبه شود. به این منظور باید حدود انتگرال را متناسب با فیزیک مسئله تعیین کنیم.
در اینجا حداکثر و حداقل مقداری که میتوانید داشته باشید و هستند. در نقاط مذکور انرژی جنبشی صفر بوده و انرژی کل تنها شامل بخش پتانسیل است. در نتیجه:
(4)
از رابطه فوق مقدار به صورت زیر نتیجه میشود:
(5)
حال تمامی متغیرهای مورد نیاز سمت چپ رابطه (۱) را در اختیار داریم. با جایگذاری آنها با توجه به تقارن مسئله در رابطه (۱) نتیجه میشود:
(6)
با استفاده از تغییر متغیر ، با توجه به فیزیک مسئله نوسانگر هماهنگ ساده، رابطه فوق به صورت زیر ساده میشود (به تغییر حدود انتگرال دقت داشته باشید):
(7)

مقدار ω (فرکانس زاویهای) به صورت با فرکانس رابطه دارد. در نتیجه:
(8)
سمت چپ رابطه (۱)، برابر با مقدار فوق شد. حال با مساوی قرار دادن رابطه فوق با مقدار (سمت راست رابطه ۱) به راحتی اصل کوانتش پلانک نتیجه میشود:
(9)
قاعده کوانتش ویلسون زومرفلد و شرط کوانتش بوهر
در این بخش در نظر داریم تا با استفاده از قاعده کوانتش ویلسون زومرفلد، شرط کوانتش بوهر/بور () را به دست آوریم. جهت آشنایی با مدل اتمی بور، پیشنهاد میکنیم تا نگاهی بر مقاله «مدل اتمی بور — به زبان ساده» داشته باشید.
مدل اتمی بور بیان میکند که الکترونها در مدارهایی دایرهای با شعاع مشخص در حال گردش هستند. بدیهی است که بهترین دستگاه مختصات برای سیستمی دایرهای، مختصات کروی یا ساده شده آن مختصات قطبی است. متغیر کنش کلاسیکی در مختصات دکارتی با تکانه خطی و مزدوج مختصه مکانی تعریف میشود.
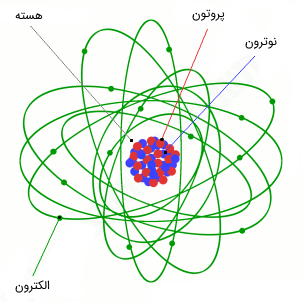
متغیرهای و مذکور در دستگاه مختصات کروی با تکانه زاویهای و (زاویه قطبی) تعریف میشوند. پیشتر بیان کردیم که انتگرال روی یک دور کامل از مختصه مکانی محاسبه میشود. در اینجا متناسب با فیزیک تعریف شده، یک دور کامل بدین معنی است که زاویه قطبی ، زاویه صفر تا را طی کند. در نتیجه متناسب با رابطه (۱) خواهیم داشت:
(10)
در اینجا الکترون تحت پتانسیل ثابت هسته (پروتون) بوده که در نتیجه تکانه زاویهای مقدار ثابتی خواهد داشت و به راحتی از انتگرال بیرون میآید. در نتیجه:
(11)
در فیزیک غالباً پارامتر را که در بسیار از مسائل ظاهر میشود، ثابت پلانک کاهش یافته مینامند. در نتیجه:
(12)
با توجه به رابطه فوق، تکانه زاویهای ، در هر مدار که با مشخص میشود (ترازهای انرژی کوانتیده)، مقدار ثابتی دارد. مدل بور بیان میکند که الکترون در مدارهای مشخصی که محیط آنها مضرب صحیحی از طول موج باشد، با تکانه زاویه مشخص به دور هسته گردش میکند.

لازم به ذکر است که در سالهای بین 1900 تا 1925 میلادی دنیای فیزیک کوانتوم محدود به اصل کوانتش پلانک و بوهر/بور بود. امروزه از این دوره ۲۵ ساله به عنوان نظریه کوانتومی قدیم (old quantum theory) یاد میکنند. موفقیت نظریه مکانیک کوانتومی در دوران تولد مدیون این دو قاعدع کوانتش است که با تجربه و آزمایشات به خوبی هماهنگ بود. این دو قاعده کوانتش با وجود موفقیت، اساس نظری خاصی نداشتند و به صورت نسبتاً دلخواهی جزء اصول موضوعه مکانیک کوانتومی قرار گرفته بودند.
قاعده کوانتش ویلسون زومرفلد و چاه پتانسیل یک بعدی
در این بخش در نظر داریم تا ترازهای انرژی کوانتیزه ذرهای را که در یک چاه پتانسیل بینهایت یک بعدی قرار دارد، به دست آوریم. پیشنهاد میکنیم جهت آشنایی کامل با چاه پتانسیل بینهایت یک بعدی به مقاله «چاه پتانسیل (Potential Well) یا ذره در جعبه — به زبان ساده» مراجعه فرمایید.
به بیانی ساده، چاه پتانسیل مفهومی است که در آن پتانسیل درون چاه صفر و روی دیوارهها بینهایت است. در این صورت ذره در چاه پتانسیل به دام میافتد. شکل زیر شماتیکی را نشان میدهد که تجسم چاه پتانسیل را سادهتر میسازد. لازم به ذکر است که مسئله چاه پتانسیل، به مسئله ذره در جعبه نیز معروف است.
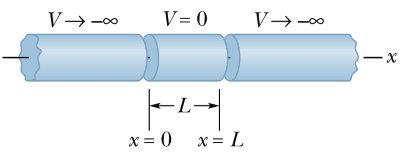
در اینجا با استفاده از انرژی مکانیکی (کل) کلاسیکی داریم:
(13)
در ادامه باید مقدار تکانه را از اصل کوانتش ویلسون زومرفیلد به دست آوریم. بدیهی است که مختصه مکانی طول چاه پتانسیل یا جعبه است. در نتیجه حدود انتگرال نیز به راحتی مشخص میشود:
(14)
(15)
حال با جایگذاری تکانه در رابطه انرژی (13) نتیجه میشود:
(16)
دقت داشته باشید که انرژی پتانسیل در رابطه (13) درطول چاه پتانسیل صفر است. با استفاده از ثابت پلانک کاهش یافته، فرم آشناتر زیر به دست میآید:
(17)
(18)
همانطور که ملاحظه میکنید، عبارت فوق همان عبارتی است که از حل معادله شرودینگر برای ساختار چاه پتانسیل یک بعدی به دست آمد.
در صورتی که به موضوعات مشابه فوق علاقهمند هستید، مطالب مرتبط زیر به شما پیشنهاد میشوند:
- پله پتانسیل (Potential Step) — به زبان ساده
- معادله شرودینگر -- به زبان ساده
- میزر (Maser) -- به زبان ساده
^^












