نرم افزار متلب چیست و چه کاربردی دارد؟ + معرفی منابع یادگیری Matlab
در این نوشتار قصد داریم در مورد نرم افزار متلب و کاربردهای آن صحبت کنیم. نرم افزار متلب یک پلتفرم برنامه نویسی است که به صورت خاص برای مهندسین و دانشمندان ارائه شده است. قلب نرم افزار متلب، امکان برنامه نویسی متلب است و زبان پایه ماتریسی آن این امکان را میدهد تا بتوانیم طبیعی ترین پدیدههای عالم را بر حسب زبان محاسباتی بیان کنیم. در این نوشته در مورد نرم افزار متلب و ویژگیهای اصلی این نرم افزار صحبت میکنیم و منابع برتر برای یادگیری آن را معرفی میکنیم.


شروع با نرم افزار متلب چگونه است؟
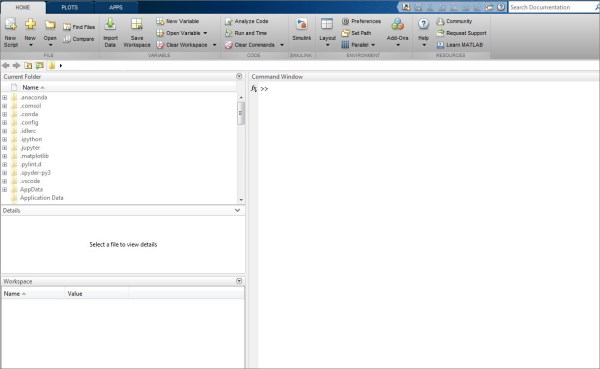
تصویر 1: صفحه ابتدایی نرم افزار متلب
وقتی متلب را باز میکنید به پنجرهای مانند تصویر بالا برخورد میکنید که در تصویر قسمتهای مختلف این صفحه نمایش داده شده است. یکی از ویژگیهای متلب این است که میتواند نحوه قرار گیری و ساختار شبکه را تغییر دهید. در صفحه Command ممکن است با دو نوع علامت در صفحه خالی Command مواجه شوید که به صورت زیر هستند:
| << | در این حالت شما ورژن کامل متلب را دارید. |
| EDU> | در این حالت ورژن آموزشی متلب در اختیار شما است. |
اما نوتیشن رایج در صفحه Command همان >> است که در ادامه ما نیز از این رویه استفاده میکنیم.
استفاده از متلب به عنوان ماشین حساب
به عنوان یک مثال از محاسبات ساده در متلب تنها لازم است عبارتی که قصد دارید محاسبه کنید را در پنجره متلب تایپ کنید. برای مثال عبارت ساده را میخواهیم محاسبه کنیم.
بدین منظور کافی است عبارت را در صفحه دستورات یا cammand تایپ کنید و با استفاده از کلید Enter جواب را در خط بعد مشاهده میکنید.
همان طور که مشاهده میکنید اگر برای جواب متغیری تعریف نشده باشد، متلب به صورت پیش فرض از ans به عنوان متغیری که جواب را در آن ذخیره کند، استفاده خواهد کرد. ولی اگر برای عبارت خود، یک متغیر مانند x تعریف کنید جواب نهایی در x ذخیره میشود، یعنی داریم:
از x میتوان به عنوان پارامتری که مقدار آن مشخص است مجدداً استفاده کرد و بدین ترتیب برای مثال داریم:
بدین ترتیب میتوان گفت علامتهای به ترتیب چهار عمل اصلی ریاضیات را در متلب انجام میدهد. برای اتمام یک session در متلب با تایپ کردن quit نرم افزار متلب بسته میشود یا میتوانید مانند تمام پنجرهها این برنامه رو نیز با کلیک بر روی ضربدر قرمز ببندید.
Overwriting در متلب
هنگامی که یک متغیر را در متلب تعریف میکنید، آن متغیر مقداری که شما تعریف کردهاید را خواهد گرفت.
اگر مجدداً روی متغیر عملیات جبری انجام دهید در حافظه متلب آخرین مقدار متغیر باقی میماند. این موضوع را در مثال زیر میتوانید ببینید:
اگر دقت کنید در معادله بالا مقدار 6 برای متغیر t در نظر گرفته شده است و این مقدار نهایی در نهایت برای محاسبات دیگر در نظر گرفته میشود.
پیام خطا
اگر یک عبارت را به اشتباه در متلب بنویسید، یک پیام خطا برای شما نمایش داده خواهد شد. برای مثال در کد زیر علامت * را ننوشتهایم.
تصحیح خطا در متلب
در بسیاری از موقعیتهایی که با پیغام خطا رو به رو میشوید، مخصوصاً اگر عبارتی که نوشتهاید طولانی باشد تایپ مجدد آن سخت است. به همین دلیل بهتر است در این مواقع دستورات قبلی را با استفاده از کلید رو به بالا () در صفحه کیبورد خود جستجو کنید و از این روش برای تصحیح خطای رخ داده در دستور خود استفاده کنید.
کنترل کردن ترتیب عملگرها در متلب
اگر دستور جمع و ضرب قبلی را این بار با پرانتز در نظر بگیریم، خواهیم دید که جواب متفاوت خواهد بود. در این صورت داریم:
در حالی که در مثال بالاتر و بدون پرانتز جواب برابر با 7 به دست آمده بود. به صورت کلی سلسله انجام مرتبههای عملیات جبری در متلب شبیه به آموزشهای مدرسه است. در متلب نیز ابتدا عملیات جبری در داخل پرانتزها انجام میشود و سپس از داخل پرانتز به سمت خارج حرکت میکنیم. در ادامه تمام موارد نمایی محاسبه میشوند و این محاسبه از چپ به راست انجام میشود. در مرحله سوم ضربها و تقسیمها از چپ به راست صورت میگیرد. در نهایت نیز همه جمعها و تفریقها از چپ به راست محاسبه میشوند. مجدداً حالت زیر را در نظر بگیرید:
این عبارت را یک بار با پرانتز و یک بار بدون پرانتز در متلب محاسبه میکنیم و داریم:
همان طور که ملاحظه میکنید بدین ترتیب از یک عبارت دو جواب متفاوت به دست آوردیم که این تفاوت، اهمیت پرانتزها را به درستی نشان میدهد.

برای آشنایی بیشتر با مبانی نرم افزار متلب، میتوانید فیلم آموزش برنامه نویسی متلب (MATLAB) را مشاهده کنید که توسط فرادرس ارائه شده، لینک این آموزش در ادامه آورده شده است.
- برای دیدن فیلم آموزش برنامه نویسی متلب (MATLAB) + اینجا کلیک کنید.
مشخص کردن تعداد اعشار در متلب
به صورت پیش فرض نرم افزار متلب تا 4 رقم اعشار نتایج را نشان میدهد. برای متلب حالت تعداد اعشار بیشتر نتایج با استفاده از دستور format long به دست میآید و مجدداً برای بازگشت به حالت دیفالت متلب میتوانیم از دستور format یا format short استفاده کنیم. این حالات را در مثال زیر ببینید.
نکته دیگر اینکه برای چاپ نشدن هر متغیری که تعریف کردهاید بعد از فشار دادن کلید Enter میتوانید در انتهای متغیر از (;) استفاده کنید.
مدیریت صفحه کار
وقتی در متلب به یک متغیر عددی بدهید تا انتهای آن Session آن مقدار برای متغیر در نظر گرفته میشود و این مورد میتواند در تعاریف بعدی توابع شما موجب خطای محاسباتی شود. بدین دلیل از دو دستور clear و clc استفاده کنید. با استفاده از دستور clear تمام متغیرهایی که تعریف کردیم را از حافظه پاک میکنیم و با استفاده از دستور clc صفحه دستورات را پاک میکنیم.
همچنین با استفاده از دستور who میتوانیم متغیرهایی که تعریف کردیم را مشاهده کنیم و دستور whos اندازه و نوع متغیرهای تعریف شده را نشان میدهد.
وارد کردن چند دستور در یک خط
همان طور که گفتیم میتوانیم بعد از تعریف یک متغیر برای جلوگیری از چاپ مجدد متغیر در انتهای آن از عبارت (;) استفاده کنیم. همچنین برای این که چندین عبارت محاسباتی را در یک خط بنویسم بین عبارتها از (,) استفاده میکنیم و با استفاه از enter تمام کمیتهای خواسته شده محاسبه و چاپ میشوند. برای درک بهتر مثال زیر را ببینید:
اگر در نیمه یک محاسبه توسط متلب میخواهید محاسبه متوقف شود میتوانید از دستور ctrl-c استفاده کنید و همچنین اگر طول یک عبارت بلند بود با استفاده از ... میتوانید ادامه عبارت را در خط بعد بنویسید.
دستور help
برای استفاده از راهنماییهای داکیومنتهای متلب به راحتی میتوانید با تایپ کردن عبارت help و دستوری که قصد جستجوی آن را دارید، از داکیومنتهای متلب استفاده کنید. برای مثال برای اینکه بدانید دستور جذر در متلب چگونه کار میکند کافی است عبارت help sqrt را تایپ کنید. به علاوه برای آشنایی با نحوه استفاده از یک دستور در متلب کافی است از عبارت doc و دستوری که قصد آشنایی با آن را دارید استفاده کنید. برای مثال برای آشنایی با نحوه استفاده از دستور plot کافی است عبارت doc plot را تایپ کنید و مستقیم داکیومنتهای مربوط به این دستور در متلب برای شما باز خواهد شد.
توابع تعریف شده در متلب
برخی از توابع مانند توابع مثلثاتی در متلب تعریف شدهاند و تنها کافی است آنها را فراخوانی کنید تا محاسبات مورد نظر خود را انجام دهید.
لیست این توابع را در ادامه میتوانید مشاهده کنید.
توابع پایه در متلب
| قدر مطلق | کسینوس | ||
| تعیین علامت تابع | سینوس | ||
| ماکزیمم مقدار | تانژانت | ||
| مینیمم مقدار | معکوس کسینوس | ||
| گرد کردن به سمت | معکوس سینوس | ||
| گرد کردن به سمت | معکوس تانژانت | ||
| گرد کردن به سمت نزدیکترین عدد صحیح | تابع نمایی | ||
| باقیمانده تقسیم | جذر | ||
| زاویه فاز | لگاریتم طبیعی | ||
| مزدوج مختلط | لگاریتم معمولی |
رسم نمودار در متلب
نمودار را میتوان با دستور plot در متلب رسم کرد. نمودار به شما کمک میکند تا مفاهیم و توابع ریاضی را راحتتر درک کنید. برای رسم یک تابع دو بعدی با استفاده از دادههای و از دستور plot(x,y) استفاده میکنیم و نتیجه را مشاهده خواهیم کرد. برای درک بهتر مثال زیر را مشاهده کنید:
دقت کنید در تعریف بالا x را بین صفر تا در نظر میگیریم که این فاصله با قدمهای طی میشود. برای اضافه کردن عنوان و برچسب برای هر یک از راستاهای نمودار از دستور title و label استفاده میکنیم، بدین ترتیب داریم:
و نمودار فراخوانی شده به شکل زیر نمایش داده میشود. دقت کنید که رنگ یک تک نمودار به صورت پیش فرض آبی است و برای تغییر رنگ آن مثلاً به قرمز، میتوان دستور را به صورت plot(x,y,’r’) بنویسیم.
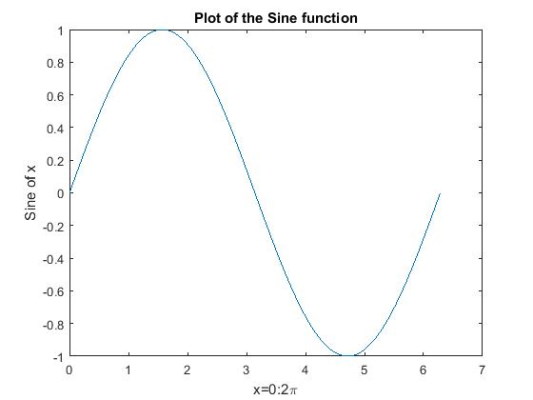
برای آشنایی بیشتر با دستورات دیگر plot میتوانید از دستور doc plot استفاده کنید.
ماتریس در متلب
ماتریسها عناصر اصلی محیط MATLAB هستند. ماتریس یک آرایه دو بعدی است که از m سطر و n ستون تشکیل شده است. موارد خاص بردارهای ستونی (n = 1) و بردارهای سطری (m = 1) هستند.
در این بخش نحوه اعمال عملیات مختلف روی ماتریسها را نشان خواهیم داد. متلب از دو نوع عملیات پشتیبانی میکند که به عملیات ماتریسی و عملیات آرایه معروف هستند. در ادامه این مباحث را به تفصیل بررسی میکنیم.
تولید ماتریس در نرم افزار متلب
همان طور که گفتیم ماتریسها عناصر اصلی در متلب هستند. ماتریسها را میتوان به روشهای مختلفی تولید کرد که در ادامه آنها را معرفی میکنیم.
- یک ماتریس سطری که برای مثال با دستور تولید میشود.
- یک ماتریس ستونی که برای مثال با دستور تولید میشود.
- ترانهاده یک ماتریس را میتوان با دستور ایجاد کرد.
- عناصر یک ماتریس v را میتوان با دستور یا فراخوانی کرد که 1 یا n شماره آرایه آن عنصر در ماتریس است.
یک ماتریس آرایهای از اعداد است. برای تعریف یک ماتریس در متلب به ترتیب موارد زیر را طی میکنیم:
- یک براکت مربعی باز میکنیم.
- عناصر در یک سطر را با فاصله یا (,) جدا میکنیم.
- عناصر یک سطر را با (;) جدا میکنیم.
- با یک براکت مربعی دیگر تعریف ماتریس را میبندیم.
- برای مثال ماتریس را به صورت زیر در متلب تولید میکنیم.
در ماتریس A که در بالا تولید شده با نوشتن دستور عنصر سطر 2 و ستون 1 را فراخوانی میکنید.برای تغییر مقادیر یک عنصر در ماتریس کافی است آن عنصر را فراخوانی کرده و برابر با مقدار جدید قرار دهید. با فراخوانی مجدد ماتریس خواهید دید که مقدار جدید جایگزین مقدار قبلی شده است.
برای حذف یک سطر یا ستون به صورت زیر عمل میکنیم:
بدین ترتیب سطر 3 از ماتریس A را حذف میکنیم. برای مشخص کردن سایز یک ماتریس نیز از دستور استفاده میکنیم و در خروجی تعداد سطر و ستون ماتریس نوشته میشود. همچنین دستورات خاصی برای تولید ماتریسهای خاص وجود دارد که آنها را در ادامه معرفی میکنیم:
| یک ماتریس m در n میدهد که قطر اصلی آن 1 است. | |
| یک ماتریس مربعی n در n میدهد که قطر اصلی آن 1 است. | |
| یک ماتریس m در n میدهد که عناصر آن صفر هستند. | |
| یک ماتریس m در n میدهد که عناصر آن یک هستند. | |
| عناصر روی قطر ماتریس A را میدهد. | |
| یک ماتریس m در n با اعداد تصادفی میدهد. |
اعمال جبری بر روی آرایههای ماتریس
چهار عمل اصلی برای ماتریسها را میتوان به صورت زیر تعریف کرد:
| المان در المان دو ماتریس در هم ضرب میشوند. | |
| المان در المان دو ماتریس بر هم تقسیم میشوند. | |
| هر المان ماتریس به توان یک عدد مشخص شده در دستور میرسد. | $$.^$$ |
همچنین برای آشنایی با رسم نمودار ماتریس در متلب اینجا را بخوانید.
حل معادلات خطی در متلب
معادله را در نظر بگیرید که A همان ماتریس سه در سه است که در قسمت قبل معرفی کردیم و b یک ماتریس یک در سه در نظر گرفته شده است.
برای محاسبه x تنها کافی است معکوس ماتریس A را در طرفین معادله ضرب کنیم و بدین ترتیب مقادیر x به دست میآید. یعنی داریم:
توابع مختلف مربوط به ماتریس را نیز میتوانید در جدول زیر مشاهده کنید.
| دترمینان | det |
| ماتریس قطری و قطر اصلی ماتریس | diag |
| ویژه مقدار و ویژه تابع | eig |
| معکوس ماتریس | inv |
| نُرم ماتریس و بردار | norm |
| تعداد سطر و ستونهای خطی مستقل | rank |
برای مطالعه بیشتر در این زمینه مطلب حل دستگاه معادلات دیفرانسیل غیر خطی در متلب | گام به گام را در مجله فرادرس بخوانید.
برنامه نویسی با نرم افزار متلب
تا کنون در مثالهای ارائه شده، همه دستورات در پنجره فرمان یا Command اجرا شده است. مشکل این است که دستورات وارد شده در پنجره فرمان را نمیتوان چندین بار ذخیره و دوباره اجرا کرد. بنابراین یک روش متفاوت برای اجرای مکرر دستورات با MATLAB این است که سه مرحله زیر را انجام دهیم:
- یک فایل با لیستی از دستورات را ایجاد کنید.
- فایل را ذخیره کنید.
- فایل را اجرا کنید.
یک فایل اسکریپت یک فایل خارجی است که شامل دستوراتی از متلب است. یک فایل اسکریپت دارای نام و یک پسوند .m است که به آن M فایل میگوییم. این فایلها میتوانند یک یا چندین خروجی داشته باشند. در اینجا دو مثال ساده را بررسی میکنیم. در ابتدا یک دستگاه معادلاتی زیر را در نظر بگیرید:
برای این دستگاه معادلاتی میخواهیم مقدار را محاسبه میکنیم. یک فایل اسکریپت را از مسیر زیر در متلب باز میکنیم:
و دستورهای زیر را در آن تعریف میکنیم:
این فایل را با نام example1.m ذخیره کرده و با تایپ کردن example1.m در صفحه دستورات این فایل را اجرا میکنیم و در نتیجه مقادیر x را به دست میآوریم:
بعد از اتمام اجرا متغیرهای A، b و x نیز در صفحه کار نمایش داده میشوند. برای ویرایش m فایل با تایپ کردن دستور edit یا edit filename.m میتوان فایل دستورات را باز کرد و تغییرات را بر آن اعمال کرد.
برای مثال دوم در نظر بگیرید که ، و هستند که قرار دارد. میخواهیم نمودار این سه تابع را با m فایل رسم کنیم. بدین ترتیب در فایل اسکریپت داریم:
این فایل را با نام example2 ذخیره میکنیم و مجدداً با تایپ کردن نام فایل در صفحه دستورات آن را اجرا میکنیم که نتایج به شکل زیر خواهند بود.
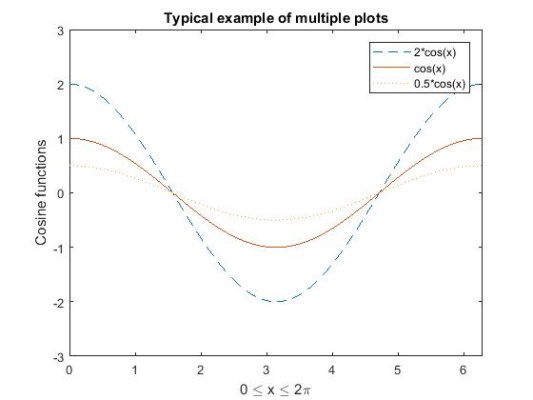
با این حال این روش تعریف دستورها ممکن است مشکلاتی داشته باشد از جمله این که:
- متغیرهای فایل اسکریپت در صفحه دستورات آورده میشوند و این موجب تعریف متغیرهایی در صفحه دستورات میشود که پیشتر تعریف کردهایم.
- اجرای اسکریپت میتواند تحت تاثیر متغیرهای حالت محیط کار متلب قرار گیرد.
به همین دلایل بهتر است از روش دیگر یعنی توابع m فایل برای تعریف مجموعهای از دستورات یا برنامه نویسیهای پیچیدهتر استفاده کنیم. تعریف تابع در متلب باید یک ورودی و یک خروجی داشته باشد که تعداد ورودیها و خروجیها با تعریف تعداد متغیر در تابع مشخص میشود. در حالت کلی برای تعریف تابع در نرم افزار متلب داریم:
| تعریف تابعی با یک ورودی و یک خروجی | function C= FtoC(F) |
| تعریف تابعی با سه ورودی و یک خروجی | function area= TrapArea(a,b,h) |
| تعریف تابعی با دو ورودی و دو خروجی | function [h,d]= motion(v, angle) |
همچنین میتوانیم از دستورات input و output نیز برای گرفتن ورودی و نمایش خروجی استفاده کنیم. برای یک مثال استفاده از input میخواهیم برنامهای بنویسیم که سه عدد را به عنوان امتیاز سه مسابقه از ما بگیرد و خروجی را محاسبه و چاپ کند، در نتیجه داریم:
با ذخیره این فایل به نام example3 و اجرای آن با تایپ نام فایل ذخیره شده در صفحه دستورات، برنامه از شما در سه مرحله مقادیری که میخواهید میانگین آنها را حساب کنید میگیرد و در نهایت میانگین محاسبه شده را چاپ میکند. در مورد دستورات output دو دستوری که به صورت متداول استفاده میشوند شامل disp یا fprintf است که کمی با هم تفاوت دارند. disp برای استفاده راحتتر است اما کنترل کمتری بر ظاهر خروجیهای نمایش داده شده دارد. اما ftprint کمی برای استفاده پیچیدهتر است اما کنترل کاملی بر ظاهر خروجی دارد.
همان طور که گفتیم متلب یک زبان برنامه نویسی است و مانند تمام زبانهای برنامه نویسی دارای حلقههای تصمیم گیری است. این حلقهها عبارت از for، while و if-else-end هستند. با استفاده از یک m فایل و اجرای آن میتوانیم به راحتی این دستورها و حلقهها را نیز اجرا کنیم. برای مثال میخواهیم با استفاده از یک حلقه if، حقیقی یا غیرحقیقی بودن ریشههای یک معادله درجه دوم را مشخص کنیم. اگر معادله را به صورت زیر در نظر بگیریم:
با دادن مقادیر a، b و c میتوانیم نوع ریشههای معادله را پیدا کنیم و داریم:
با ذخیره کردن این فایل و اجرای آن میتوانید نوع ریشههای یک معادله درجه دوم را مشخص کنید.
سیمولینک متلب چیست؟
سیمولینک یک محیط بلوک دیاگرام برای شبیه سازی چند حوزهای و طراحی مبتنی بر مدل است. این برنامه از طراحی در سطح سیستم، شبیه سازی، تولید خودکار کد و آزمایش و تأیید مداوم سیستمهای تعبیه شده پشتیبانی میکند. سیمولینک یا Simulink یک ویرایشگر گرافیکی، کتابخانههای بلوک قابل تنظیم و حل کنندهها را برای مدل سازی و شبیه سازی سیستمهای پویا ارائه میدهد. این نرم افزار با متلب تجمیع شده است و به شما این امکان را میدهد که الگوریتمهای نرم افزار متلب را در مدلها بگنجانید و نتایج شبیه سازی را برای تجزیه و تحلیل بیشتر به متلب صادر کنید. برای آشنایی بیشتر با این مفهوم مطلب آشنایی با سیمولینک — راهنمای کاربردی را در مجله فرادرس بخوانید.
معنی متلب چیست؟
نام نرم افزار متلب مخفف «آزمایشگاه ماتریس» (Matrix Labratory) است. متلب در اصل برای دسترسی آسان به نرم افزارهای ماتریسی توسعه یافت و توسط پروژههای LINPACK و EISPACK نوشته شد، که حاصل کار آنها نشان دهنده پیشرفته ترین نرم افزار برای محاسبه ماتریسی است.
متلب طی چند سال با استفاده از بسیاری از کاربران تکامل یافته است. در محیطهای دانشگاهی، این ابزار استاندارد آموزشی برای دورههای مقدماتی و پیشرفته ریاضیات، مهندسی و علوم است. در صنعت نیز متلب ابزار انتخاب برای تحقیق، توسعه و تجزیه و تحلیل با بهره وری بالا است.
دستور eval در متلب چیست؟
در نرم افزار متلب دستور eval(expression) یک دستور همه کاره است که میتوانید به راحتی از آن برای اهداف مختلف استفاده کنید. در اینجا نحوه استفاده از دستور ()eval را در مثالهای مختلف انجام شده در پنجره فرمان متلب به شما آموزش میدهیم.
برای شروع کار با این دستور کد زیر را در صفحه Command متلب نظر بگیرید:
همان طور که در مثال بالا مشاهده کردید، میتوانید از دستور ()eval با تایپ کردن تابع داخل آن استفاده کنید. a یک بردار است و این بردار دارای ده عنصر است که از 1 تا 10 تغییر میکنند. ما یک تابع را در دستور ()eval در داخل علامت مربوط به نقل قولها تایپ کردیم، که در آن متغیر a است. نام دستور ()eval را برابر با b قرار دادیم. در نهایت بردار b با توجه به تابع درون آن مقادیر جدید a را چاپ میکند. مثالی دیگر با این دستور را در ادامه میبینید:
در این مثال ماتریس سه در سه، x تعریف شده است و میخواهیم تمام مقادیر منفی را به صورت قدر مطلق این آرایهها نمایش دهیم. بدین ترتیب از دو حلقه for با توجه به ماتریس استفاده کردیم و در آن با دستور eval() تعریف کردیم، که اگر مقدار این آرایه کوچکتر از صفر بود قدر مطلق این مقدار را نمایش دهد که در ادامه نتایج نمایش داده شده است.
دستور syms در متلب چیست؟
در نرم افزار متلب دستورهای sym و syms برای تولید توابع سمبلیک استفاده میشود. این دو دستور یعنی sym و syms با هم تفاوتهایی دارند که در ادامه آنها را توضیح میدهیم.
تابع syms متغیری را به صورت پویا ایجاد میکند. به عنوان مثال دستور syms x متغیر نماد x را ایجاد میکند و به طور خودکار آن را به متغیرهای متلب با همان نام اختصاص میدهد. اما تابع sym به یک متغیر نمادین اشاره دارد که میتوانید آن را به متغیر متلب با نام متفاوت اختصاص دهید. به عنوان مثال دستور f1 = sym ('x') به متغیر نمادین x اشاره دارد و آن را به متغیر f1 متلب اختصاص میدهد.
دستور fft در متلب چیست؟
دستور Y = fft (X) تبدیل گسسته فوریه (DFT) عنصر X را با استفاده از الگوریتم تبدیل سریع فوریه (FFT) محاسبه میکند. در این حالت اگر X بردار باشد، fft (X) تبدیل فوریه بردار را برمیگرداند. اگر X یک ماتریس باشد، fft (X) ستونهای X را به عنوان بردار در نظر میگیرد و تبدیل فوریه هر ستون را برمیگرداند.
در نهایت اگر X یک آرایه چند بعدی باشد، fft (X) مقادیر اولین بعد آرایه را که اندازه آن برابر 1 نیست به عنوان بردارها در نظر میگیرد و تبدیل فوریه هر بردار را بر میگرداند. در ادامه با استفاده از این دستور اجزای فرکانس سیگنال دفن شده در نویز را محاسبه میکنیم. برای شروع کار پارامترهای یک سیگنال با فرکانس نمونه 1 کیلوهرتز و مدت زمان 1/5 ثانیه را مشخص میکنیم.
در ادامه یک سیگنال سینوسی 50 هرتز با دامنه 0/7 و یک سیگنال سینوسی 120 هرتز با دامنه 1 تشکیل میدهیم:
سپس سیگنال را با نویز سفید با میانگین صفر با واریانس 4 مختل میکنیم و داریم:
سیگنال نویز را در حوزه زمان ترسیم کرده و خواهید دید که تشخیص اجزای فرکانس با نگاه به سیگنال X (t) دشوار است.
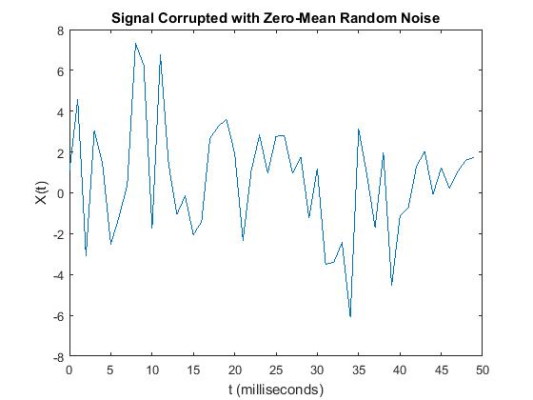
با تبدیل فوریه سیگنال را محاسبه میکنیم و داریم:
سپس طیف دو طرفه P2 را محاسبه کرده و طیف یک طرفه P1 را بر اساس P2 و طول سیگنال برابر L محاسبه میکنیم:
حوزه فرکانس f را تعریف کرده و طیف دامنه یک طرفه P1 را رسم میکنیم. به دلیل نویز اضافی، دامنهها همانطور که انتظار میرود دقیقاً در 0/7 و 1 نیستد و به طور متوسط سیگنالهای طولانی، تقریب فرکانس بهتری تولید میکنند.
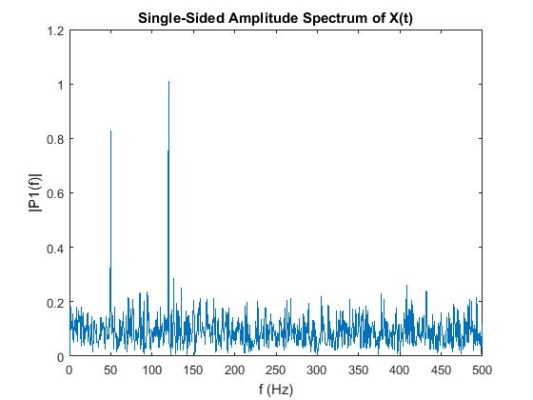
سپس تبدیل فوریه سیگنال اصلی، بدون اختلال را در نظر گرفته و میبینیم دامنههای دقیق 0/7 و 1/0 به دست میآیند.
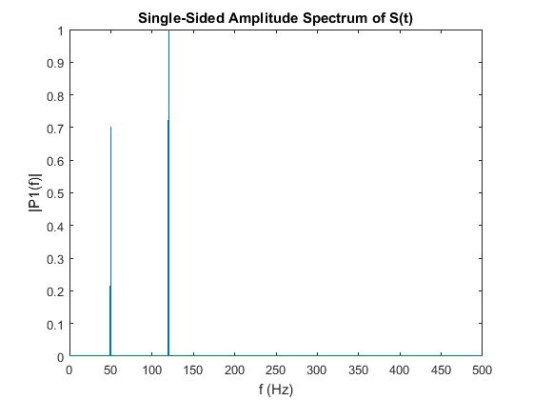
منابع برتر نرم افزار متلب
همان طور که گفتیم نرم افزار متلب یک زبان برنامه نویسی مبتنی بر ماتریس است که توسط MathWorks توسعه یافته است و پلتفرم برنامه نویسی نرم افزار متلب به طور خاص برای مهندسان و دانشمندان طراحی شده است. در این قسمت برخی از بهترین کتابهای نرم افزار متلب را برای شما بررسی و معرفی میکنیم. نرم افزار متلب به سرعت تبدیل به بهترین ابزار محاسبه دادههای مختلف شده است. این نرم افزار برای تجزیه و تحلیل دادهها، توسعه الگوریتمها، پیاده سازی الگوریتمها، تغییرات در ماتریسها، ترسیم توابع و دادهها، ایجاد مدلها و برنامهها و ارتباط با برنامهها و غیره استفاده میشود.
متلب توسط میلیونها مهندس و دانشمند برای طیف وسیعی از کاربردها مانند یادگیری ماشین و Deap Learning نیز مورد استفاده قرار میگیرد. برای شروع کار با متلب، باید با زبان برنامه نویسی شی گرا مانند C یا C++ آشنایی داشته باشید.
همچنین برای یادگیری و ایجاد تعدادی برنامه کاربردی در دنیای واقعی، میتوانید از کتاب MATLAB & Simulink Student Suite استفاده کنید. با افزایش دامنه مشاغل علم داده در سراسر جهان، یادگیری نرم افزار متلب میتواند تصمیم خوبی برای شما باشد و همچنین یادگیری آن آسان است. در ادامه برخی کتابهای مفید برای آموزش متلب را معرفی میکنیم.
کتاب متلب: مقدمهای کاربردی در برنامه نویسی و حل مسائل

اگر به دنبال یک مرور خوب از نرم افزار متلب هستید، کتاب متلب: مقدمهای کاربردی در برنامه نویسی و حل مشکلات توسط استورمی اتتاوی یک گزینه خوب برای شما به شمار میآید. در این کتاب شما هم برنامه نویسی و هم ساخت توابع را یاد خواهید گرفت تا بتوانید به راحتی از قابلیتهای قدرتمند نرم افزار متلب برای مقابله با مشکلات مهندسی و علمی استفاده کنید. این کتاب هیچ دانش برنامه نویسی قبلی را در نظر نمیگیرد و مفاهیم اولیه برنامه نویسی مانند متغیرها، نامگذاری دادهها و دستورات انتخاب، حلقهها و غیره را به شما آموزش میدهد. این کتاب دارای یک طرح خوب برای یادگیری نرم افزار متلب است و اگر در آغاز مسیر یادگیری متلب هستید بسیار برای شما توصیه میشود. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
کتاب برنامه نویسی متلب برای مهندسان

کتاب برنامه نویسی متلب برای مهندسین توسط استفن جی چپمن به شما یاد میدهد که چگونه در نرم افزار متلب برنامههای تمیز و کارآمد بنویسید. در این کتاب شما با اصول برنامه نویسی و حل مسئله و موضوعات پیشرفته مانند I/O، برنامه نویسی شی گرا و رابط کاربری گرافیکی (GUI) آشنا خواهید شد. این کتاب شامل 864 صفحه است و میتواند به عنوان ابزار مرجع برای کار با MATLAB مورد استفاده قرار گیرد. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
سری کتابهای Dummies، متلب

کتاب MATLAB For Dummies یک کتاب برای مبتدیان است و به شما نحوه ترسیم نمودارها، حل معادلات و نحوه نوشتن سریع کد را در نرم افزار متلب آموزش میدهد. در این کتاب شما اصول زبان متلب مانند سینتکس، عملگرها و انواع دادهها را خواهید آموخت. همچنین نحوه استفاده از مهمترین پنجره در نرم افزار متلب یعنی پنجره فرمان یا Command را میآموزید. شما خواهید فهمید که چگونه میتوانید کار خود را با اسکریپتها و توابع برنامه نویسی به صورت خودکار انجام دهید و نمودارها را به سرعت به صورت دو بعدی و سه بعدی رسم کنید تا دادههای خود را به صورت نمودار به تصویر درآورید. این کتاب برای مبتدیان که میخواهند بر نرم افزار محبوب متلب تسلط پیدا کنند، بسیار توصیه میشود. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
کتاب متلب برای دانشمندان مغز و علوم شناختی

کتاب متلب برای دانشمندان مغز و علوم شناختی که توسط مایک ایکس کوهن تالیف شده است مقدمهای برای نرم افزار متلب در زمینه تحقیقات علوم اعصاب ارائه میدهد. در این کتاب شما نحوه برنامه نویسی در متلب را برای ایجاد برنامههایی که بیشتر در زمینه علوم اعصاب و روانشناسی استفاده می شود یاد خواهید گرفت. در پایان فصلهای این کتاب تمرینات زیادی برای آزمایش و تقویت یادگیری خواهید داشت. در طول کتاب، مصاحبههایی با چندین عصب شناس و دانشمند علوم شناختی خواهید یافت که دانش خود را با شما به اشتراک میگذارند. روی هم رفته این مجموعه یک کتاب عالی در زمینه یادگیری برنامه نویسی متلب برای تجزیه و تحلیل دادهها توسط متخصصان نوروساینس است. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
کتاب متلب برای مبتدیان: رویکردی آهسته

کتاب متلب برای مبتدیان: رویکردی آهسته که توسط پیتر I. کاتن تالیف شده است، یک کتاب عالی برای یادگیری نرم افزار متلب از ابتدا است. این کتاب برای مبتدیان و دانشجویانی که مایل به یادگیری و تسلط بر زبان متلب هستند، طراحی شده است. برخی از موضوعات مورد بحث در این کتاب عبارت از عملیات حساب، متغیرها، توابع ریاضی، اعداد مختلط، بردارها، ماتریسها، نمودارها، معادلات و حساب و غیره هستند. این کتاب شامل حدود 230 تمرین است تا بتوانید آموختههای خود را آزمایش کنید. در حقیقت همان طور که از نام کتاب نیز مشخص است، این مجموعه روش آهسته برای یادگیری نرم افزار متلب را به شما نشان میدهد. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
کتاب راهنمای نرم افزار متلب: برای مبتدیان و کاربران با تجربه

کتاب راهنمای نرم افزار متلب: برای مبتدیان و کاربران با تجربه بسیار خوب نوشته شده است و مقدمهای کلی در مورد نرم افزار متلب را ارائه میدهد. در این کتاب شما تمام دستورات ضروری نرم افزار متلب و نحوه استفاده از ویژگیهای برنامه نویسی متلب مانند قابلیتهای گرافیکی، مدلهای شبیه سازی و رابط کاربری غنی را یاد خواهید گرفت. این مجموعه یک کتاب ایده آل برای کاربران مبتدی و با تجربه برای یادگیری نرم افزار متلب است. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
آشنایی مهندسین با برنامه نویسی در نرم افزار متلب

آشنایی مهندسین با برنامه نویسی در نرم افزار متلب 2019، یک کتاب خوب است که به شما میآموزد که چگونه از آخرین نسخههای محیط برنامه نویسی قدرتمند نرم افزار متلب و همچنین مهارتهای برنامه نویسی در متغیرها، آرایهها، ساختارها، حلقه، دستورهای شرطی و غیره استفاده کنید. آموزش های گام به گام برای کمک به شما در استفاده از متلب در این مجموعه پیدا میشود و در پایان هر فصل تعدادی تمرین برای یادگیری شما وجود دارد. برای آشنایی با جزئیات و سرفصلهای این کتاب اینجا را ببینید.
معرفی فیلمهای آموزش متلب فرادرس
منابع آموزشی نرم افزار متلب بسیار فراوان هستند اما بسیاری از منابع به زبان انگلیسی بوده که این موضوع آموزش را برای کسانی که ممکن است به زبان انگلیسی آشنایی کامل نداشته باشند دشوار میکند. همچنین با توجه به اینکه دسترسی به وبسایت متلب به صورت کامل برای کاربران ایرانی فراهم نیست، ممکن است فرآیند آموزش و شبیه سازی با این نرم افزار دشوارتر شود. به این دلیل فرادرس مجموعه دورههای آموزش متلب را برای کاربران با کاربردهای مختلف ضبط و آماده کرده است. این آموزشها را به صورت فهرست وار در ادامه معرفی میکنیم و برخی از آنها را به صورت جزئیتر برای شما توضیح میدهیم. مجموعه آموزش متلب فرادرس شامل موارد زیر هستند:
- آموزش برنامه نویسی متلب (MATLAB)
- آموزش برنامه نویسی متلب برای علوم و مهندسی
- مجموعه آموزش های برنامه نویسی متلب پیشرفته
- آموزش طراحی رابط گرافیکی کاربر (GUI) با متلب (MATLAB) - مقدماتی
- آموزش طراحی رابط گرافیکی کاربر (GUI) با متلب (MATLAB) - تکمیلی
- آموزش ساخت ربات تلگرام با متلب (MATLAB)
- آموزش کدهای بلوکی در متلب (MATLAB)
- مجموعه آموزش های واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک
- آموزش رایگان نکات و ترفندهای متلب
- آموزش آشنایی با تولباکس k-Wave در متلب
معرفی فیلم مجموعه آموزشهای برنامه نویسی متلب پیشرفته
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم مجموعه آموزشهای برنامه نویسی متلب پیشرفته کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و برای دانشجویان رشتههای علوم پایه و مهندسی مفید است. پیشنیاز این درس آموزش برنامه نویسی متلب (MATLAB) است.
درس اول این مجموعه به معرفی و آشنایی با ساختارها و آرایههای سلولی در متلب میپردازد و درس دوم عبارات قانونمند (Regular Expressions) و کاربردهای آنها در متلب را معرفی میکند. درس سوم به رویکردهای پیشرفته تعریف و پیاده سازی توابع در متلب اختصاص دارد. در درس چهارم تعریف آرایههای توسعه یافته با Container Map را در متلب خواهید آموخت و در درس پنجم این مجموعه مدیریت خطا و حالات استثنائی برنامهها در متلب آموزش داده میشود. درس ششم به تایمرها (Timer) و کاربرد آنها در متلب اختصاص دارد و در نهایت در درس هفتم این مجموعه برنامه نویسی شی گرا (Object-Oriented Programming) در متلب آموزش داده میشود.
- برای دیدن فیلم مجموعه آموزشهای برنامه نویسی متلب پیشرفته + اینجا کلیک کنید.
معرفی فیلم مجموعه آموزش های واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم مجموعه آموزشهای واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و پیشنیاز آن آشنایی با برنامه نویسی متلب، فیزیک و ریاضیات دانشگاهی است.
درس اول این مجموعه مقدمهای بر واقعیت مجازی در محیط MATLAB و Simulink است و درس دوم آشنایی با نرم افزار V - Realm Builder را آموزش میدهد. درس سوم شامل شبیه سازی انتقال یک مکعب است و درس چهارم به نحوه شبیه سازی نوسان سیستم دو درجه آزادی جرم – فنر – میراگر اختصاص دارد. در درس پنجم و ششم انیمیشن انتقال یک مکعب با استفاده از مدل Simulink و انیمیشن نوسان سیستم جرم – فنر – میراگر با استفاده از مدل سیمولینک آموزش داده میشود. در نهایت، در درس هفتم و آخر این مجموعه آشنایی با مدلهای از پیش آماده شده جعبه ابزار واقعیت مجازی آموزش داده خواهد شد.
- برای دیدن فیلم مجموعه آموزشهای واقعیت مجازی و ساخت انیمیشن برای کاربران متلب و سیمولینک + اینجا کلیک کنید.
فیلم آموزش نکات و ترفندهای متلب
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش رایگان نکات و ترفندهای متلب کرده است. این مجموعه آموزشی از بیست قسمت تشکیل شده و برای دانشجویان رشتههای مهندسی و علوم پایه مفید است. اگر قصد دارید دستورات مهم متلب را در زمان کوتاه فرا بگیرید، این مجموعه آموزشی بسیار مفید است.
درس اول این مجموعه به آشنایی با محیط متلب، توابع clc و clear و متغیر ans و درس دوم توابع سازنده ماتریسهای مهم مانند zeros ،ones و eye آموزش داده میشود. درس سوم ثابتها و علامتهای مهم و پرکاربرد در متلب را آموزش میدهد و درس چهارم شامل تشخیص محدود، نامحدود و نامعین بودن توابع (توابع ifinite ،isinf و isnan) است. درس پنجم و ششم به ترتیب عملگرهای مهم برای تعریف ماتریسها و کلمات کلیدی متلب و تابع iskeyword را پوشش میدهد. درس هفتم و هشتم شامل صفحهبندی خروجیهای طولانی با تابع more و قالببندی خروجی با تابع format است. درس نهم و دهم شامل آموزش نمادها و توابع true و false برای مقادیر منطقی و استخراج قطر ماتریس و ساخت ماتریس قطری با تابع diag هستند.
در درس یازدهم ساخت ماتریسهای قطری بلوکی با تابع blkdiag و در درس دوازدهم کاربردهای عملگر کولون یا دو نقطه و قواعد اندیسگذاری آموزش داده میشود. کاربرد کلمه end به عنوان اندیس و محاسبه ترانهاده و ترانهاده مزدوج ماتریسها در درس سیزدهم و چهاردهم بررسی میشود. در درس پانزدهم و شانزدهم آموزش دستورهای مربوط به آینهای کردن ماتریسها با تابع flip و حالات خاص آن با دو تابع flipud و fliplr و ساخت دنباله حسابی با تابع linspace پوشش داده میشود. درس هفدهم به ساخت دنباله هندسی با تابع logspace اختصاص دارد و درس هجدهم کامنتگذاری و بلوکهای کامنت در متلب را آموزش میدهد. در نهایت نیز در درس نوزدهم و بیستم فراخوانی فرمانهای سیستمی در متلب با عملگر ! و الحاق ماتریسها با تابع cat و حالات خاص آن horzcat و vertcat آموزش داده میشود.
- برای دیدن فیلم آموزش رایگان نکات و ترفندهای متلب + اینجا کلیک کنید.
جمعبندی
در این مطلب در مورد نرم افزار متلب و ویژگیهای آن صحبت کردیم. همچنین برخی از ویژگیهای اصلی نرم افزار متلب و کدهای ابتدایی در این نرم افزار را معرفی کردیم. سپس در معرفی منابع هفت کتاب برتر در زمینه آموزش متلب را معرفی کرده و در نهایت ویدیوهای آموزش متلب فرادرس را نیز مورد بررسی قرار دادیم.