رشد توابع در ساختمان داده – آموزش کامل به زبان ساده

رشد توابع به سرعت رشد مقدار تابع، همزمان با بزرگتر شدن مقدار ورودی گفته می‌شود. بیشتر اوقات رشد توابع در ساختمان داده برای تحلیل پیچیدگی زمانی الگوریتم‌ها استفاده می‌شود. مثلا می‌توانیم رشد توابع مختلف را با یکدیگر مقایسه کنیم. چند مورد از مهم‌ترین توابع شامل توابع ثابت، لگاریتمی، خطی، درجه دو و درجه سه هستند. در ادامه مطلب به شکل کامل با این توابع آشنا می‌شویم. وقتی با الگوریتم‌ها و ساختارهای داده کار می‌کنیم، باید بدانیم که زمان اجرای هر تابع چطور زیاد می‌شود. با شناخت رشد توابع، می‌توانیم مقیاس‌پذیری الگوریتم‌ها را بهتر پیش‌بینی کنیم. مخصوصا وقتی که اندازه داده‌ها بزرگتر می‌شود. همه برنامه نویسان با این مشکل روبه‌رو شده‌اند که برنامه نوشته شده آن‌ها به خوبی بر روی داده‌های کوچک کار می‌کند. اما بعد از افزایش حجم داده‌ها ورودی، زمان اجرای عملیات ناگهان خیلی کند می‌شود. در چنین موقعیت‌هایی، باید از ابزارهایی استفاده کنیم که میزان کارآمدی هر الگوریتم‌ را مشخص می‌کنند.

در این مطلب از مجله فرادرس مسئله رشد توابع در ساختمان داده را بررسی کرده‌ایم. ابتدا این مفهوم را تعریف کرده و سپس با کمک مثال‌های ساده‌ انواع نرخ رشد تابع را بررسی کردیم. همچنین درباره «نماد $$O$$ بزرگ» (Big O Notation) صحبت کرده و روش محاسبه آن را نیز بیان کرده‌ایم. در پایان هم نکات بهینه‌سازی کدها را همراه با مثال‌های مناسبی بررسی کردیم.

رشد توابع در ساختمان داده چیست؟

رشد توابع در ساختمان داده به اندازه بزرگ شدن تابع همزمان با افزایش تعداد پارامتر ورودی گفته می‌شود. زمان لازم برای اجرای الگوریتم‌ها یا توابع به اندازه داده‌ها یا پارامترهای ورودی بستگی دارد. چیزی که در چنین موقعیت‌های از اهمیت واقعی برخوردار است زمان دقیق اجرای عملیات نیست. نکته مهم، چگونگی افزایش زمان اجرای عملیات با توجه به رشد اندازه داده‌های ورودی است. معمولا محاسبه زمان دقیق اجرا بسیار سخت است. زیرا این زمان به فاکتور‌های دیگری هم مانند کامپیوتر، پیکر‌بندی‌های نرم‌افزار و سخت‌افزار و محیط کاری وابسته است.

در ادامه مطلب، مقیاس‌پذیری و نرخ رشد توابع در ساختمان داده را با روش ریاضی توضیح داده‌ایم. استفاده از این ابزارها به برنامه نویسان کمک می‌کند تا الگوریتم‌ها را بهتر مقایسه کنند.

رایج‌ترین توابع برای نمایش مقیاس‌پذیری

برای شروع تحلیل ساده ریاضی، چند مورد از توابع ساده‌ را فهرست کرده‌ایم. این تابع‌ها رایج‌ترین توابع کاربردی برای تحلیل مقیاس‌پذیری هستند.

هر وقت که صحبت از رشد توابع در ساختمان داده می‌‌شود به احتمال بسیار زیاد تابع مورد نظر از یکی از الگو‌های زیر پیروی می‌کند.

• توابع «ثابت» (Constant): برای مقادیر ثابت $$c$$ به کار برده می‌‌شود.
• توابع لگاریتمی: با فرمول $$logn$$ نمایش داده می‌شوند. به طور معمول پایه لگاریتم در این توابع ۲ در نظر گرفته می‌شود.
• توابع خطی: $$n$$
• توابع «Linearithmic» :$$nlogn$$
• توابع «مربعی» یا «درجه دوم» (Quadratic): با فرمول کلی $$n^{2}$$
• توابع «درجه سه» (Cubic): با فرمول کلی $$n^{3}$$
• توابع «چند جمله‌ای» (Polynomial): شکل کلی این توابع $$n^{k}$$ است که به‌ازای k-های بزرگتر از صفر به کار برده می‌‌شوند.
• توابع «نمایی» (Exponential): شکل کلی این توابع $$D^{n}$$ است که به‌ازای D-های بزرگتر از یک به کار برده می‌‌شوند.
• توابع فاکتوریل: با فرمول کلی $$n!$$

در ادامه مطلب برای هر کدام از اعضای فهرست بالا مثال‌های مختلفی را درباره زمان اجرای تابع بررسی کرده‌ایم.

بررسی و مقایسه رشد توابع در ساختمان داده

در ابتدا رفتار توابع رایج را با یکدیگر مقایسه می‌کنیم. به این ترتیب نشان داده‌ایم که سرعت رشد توابع مختلف در ساختمان داده به‌ازای افزایش $$n$$ چه قدر با هم تفاوت دارند.

در کادر زیر، به‌ازای محور $$Y$$ خطی تمام توابع $$1$$ و $$logn$$ و $$n$$ و $$nlogn$$ و $$n^2$$ و $$n^3$$ و $$2^n$$ و $$n!$$ را رسم کرده‌ایم.

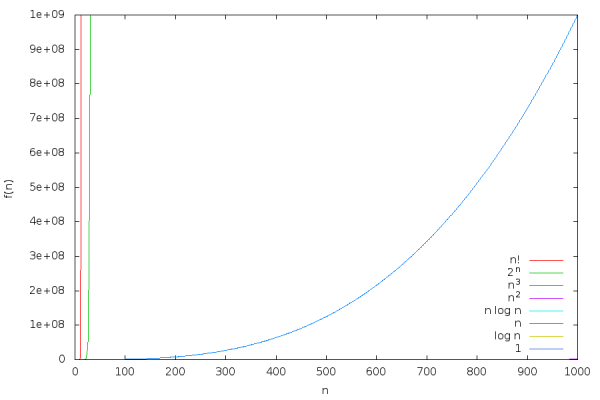
در نمودار بالا به نظر می‌رسد توابع $$n!$$ و $$2n$$ نسبت به سایر توابع با سرعت بسیار بیشتری رشد می‌کنند. سایر توابع بسیار کوچک بوده و به سادگی قابل تشخیص نیستند. بنابراین محور $$Y$$ را به مقیاس لگاریتمی تبدیل می‌کنیم.

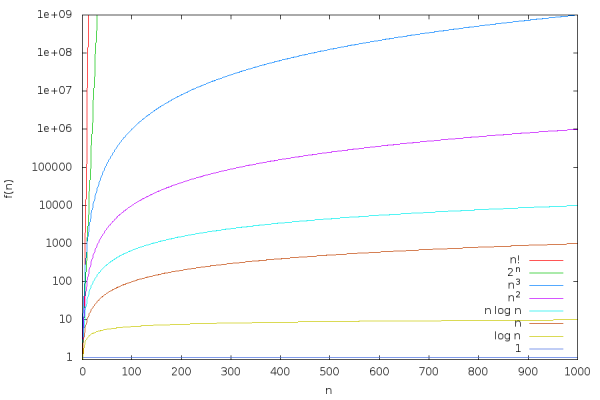
با توجه و تحلیل نمودارهای رسم شده اطلاعات مشخصی را بدست میاوریم. برای مثال بعضی از این اطلاعات را در فهرست زیر بیان کرده‌ایم.

• تابع لگاریتمی $$logn$$ با سرعت بسیار کمی رشد می‌کند. برای نمونه حاصل جواب $$log10^{9}$$ تقریبا برابر با ۳۰ است. در نتیجه می‌توانیم $$logn$$ را تا حد زیادی معادل تابع ثابت در نظر بگیریم. همین‌طور تابع $$nlogn$$ را هم می‌توان مانند تابع خطی در نظر گرفت.
• توابع چند جمله‌ای با درجه پایین مانند $$n$$ و $$n^2$$ هم به شکل آهسته رشد می‌کنند.
• اما توابع $$n!$$ و $$2^n$$ مستقیم و با سرعت زیادی در نمودار به سمت بالا حرکت می‌کنند.

برای کمک به درک بهتر مطلب، داده‌های مربوط به نمودار بالا را در جدول زیر هم نمایش داده‌ایم.

برای درک بهتر اعداد بزرگ نوشته شده در جدول بالا، فرض می‌کنیم که هر واحد برابر با ۱ نانوثانیه است. هر نانوثانیه معادل «یک میلیونیوم ثانیه» ($$10^{-9}$$) یا حدود ۳ چرخه کلاک در پردازنده‌های مدرن با سرعت ۳ گیگاهرتز است.

با این فرض، جدل بالا به شکل زیر تبدیل می‌شود.

با در نظر گرفتن نرخ رشد توابع در ساختمان داده، ۲ مسئله مهم را می‌توان مشاهده کرد.

1. فرض کنیم اگر الگوریتمی به تعداد $${n}^2$$ باز اجرا شود، می‌توانیم تعداد $$n$$ مقدار داده ورودی را در زمان $$t$$ مدیریت کنیم. بنابراین برای حل کردن مسئله‌ای با اندازه $$\sqrt{2}\times n$$ داده ورودی، در زمان یکسان $$t$$ نیاز داریم که از کامپیوتری با دوبرابر سرعت استفاده کنیم.
2. فرض کنیم زمان اجرای الگوریتمی به اندازه $${2}^n$$ طول بکشد. همچنین زمان مورد نیاز به‌ازای حل مسئله‌ای با $$n$$ تعداد ورودی برابر با $$t$$ است. در این حالت برای اینکه مسئله‌ای با $$n+1$$ تعداد داده ورودی را در همان زمان $$t$$ حل کنیم باید کامپیوتری را با دوبرابر سرعت بیشتر به کار بگیریم.

به طور کلی وقتی که اندازه داده‌های ورودی به مقدار $$n^k$$ افزایش پیدا می‌کند. کامپیوتری با دوبرابر سرعت می‌تواند داده‌هایی به اندازه $$2^{1/k}$$ بار بزرگتر را در همان زمان حل کند. اما وقتی که اندازه داده‌ها با روند $$d^n$$ افزایش پیدا کند، کامپیوتری که دوبرابر سریع‌تر است فقط می‌تواند داده‌های ورودی با اندازی $$(log2 / logd)$$ بیشتر را در زمان $$t$$ حل کند.

زیرا «رشد نمایی» (Exponential Growth) سرعت بسیار بیشتری نسب به افزایش «رشد عبارت‌های چندجمله‌ای» (Polynomial Growth) دارد.

نماد O بزرگ

نماد O بزرگ روش استانداردی برای بیان رشد توابع است. عبارت $$f(n)= O(g(n))$$ به معنای این است که $$f(n)$$ همزمان که $$n$$ زیاد می‌شود، در بیشترین حالت به اندازه $$g(n)$$ رشد پیدا می‌کند.

در این بخش از مطلب، با ابزار ریاضی برای نمایش و مقایسه نرخ رشد توابع آشنا می‌شویم که به نام «نماد $$O$$ بزرگ» (Big O Notation) شناخته می‌شود. البته نماد «نماد $$O$$ بزرگ»، هم برای محاسبه پیچیدگی زمانی به کار برده می‌شود و هم برای محاسبه پیچیدگی فضایی. برای آموزش این تکنیک پیشنهاد می‌کنیم که فیلم آموزش مروری بر پیچیدگی محاسبات Computational Complexity را در فرادرس مشاهده کنید. لینک مربوط به این فیلم را در پایین نیز قرار داده‌ایم.

این نماد با نادیده گرفتن برخی از جزئیات، بر مقیاس‌پذیری عملیات و الگوریتم‌ها تمرکز دارد. این جزئیات را در فهرست زیر آورده‌ایم.

1. اندازه‌های کوچک: در واقع تعداد کم داده‌های ورودی را نادیده می‌گیرد.
2. ضریب‌های ثابت: این ضریب‌ها معمولا به‌خاطر عواملی مانند سرعت پردازنده، پهنای باند حافظه و عملکرد پایپ‌لاین ایجاد می‌شوند.

با اینکه از نماد $$O$$ بزرگ برای بررسی زمان اجرا استفاده می‌‌شود اما می‌توان از آن برای تجزیه و تحلیل روش کار سایر منابع هم استفاده کرد.

فرض کنیم $$f$$ و$$g$$ توابعی هستند که به عنوان ورودی اعداد صحیح مثبت می‌پذیرند. این توابع در خروجی هم اعداد حقیقی، رابطه‌ای یا صحیح مثبت برمی‌گردانند. می‌گوییم که $$f$$ تابعی از $$O(g)$$ است یا $$f$$ به سرعت $$g$$ رشد می‌کند. در نتیجه اگر مقدار کافی از $$n$$ داده ورودی وجود داشته باشند، برای مقادیر ثابت $$c\geq 0$$، تابع $$f(n)$$ در بدترین حالت برابر با $$c * g(n)$$ است.

تعریف ریاضی نماد O بزرگ

نماد $$O$$ را چنین تعریف می‌کنیم که برای دو تابع $$f$$ و$$g$$ که برای کار با $$n$$ تعداد عدد صحیح مثبت تعریف شده‌اند، می‌نویسیم:

$$f(n)=O(g(n))$$

اگر ثابت‌های $$c \gt 0$$ و $$n_0 \gt 0$$

این ثابت‌ها نشان می‌دهند که برای تمام $$n$$-های بزرگ‌ترمساوی از $$n_0$$ یا $$n \ge n_0$$ رابطه $$f(n) ≤ c * g(n)$$ بر قرار است.

در این تعریف، شرط «به‌ازای تمام $$n$$-های بزرگ‌ترمساوی از $$n_0$$ یا $$n ≥ n_0$$» تاثیر اندازه‌های کوچک در تعداد داده‌های ورودی را حذف می‌کند. شرط « $$f(n) ≤ c * g(n)$$» هم پارامترهای ثابتی مانند سرعت کلاک پردازنده را حذف می‌کند.

به عبارت دیگر اگر $$f(n) = O(g(n))$$ باشد، در نتیجه$$g$$ کران بالای رشد تابع $$f$$ است. یعنی اینکه تابع $$f$$ در بدترین حالت به اندازه$$g$$ رشد می‌کند. این قائده وقتی جواب می‌دهد که از شرط‌های زیر پیروی کنیم.

• تعداد داده‌های ورودی به اندازه کافی بزرگ باشند.
• از ضریب‌های معادله صرف نظر کنیم.

مثالی برای محاسبه O بزرگ

برای مثال، تساوی $$100n^2+n+50 = \mathcal{O}(n^2)$$ برقرار است. زیرا به‌ازای تمام $$n$$-های بزرگتر‌مساوی ۸ عبارت $$100n^2+n+50 \le 101n^2$$ بر قرار است. این مسئله به معنای آن است که به‌ازای $$n‌$$-های بزرگ تابع « $$100n^2+n+50$$» در بیشترین حالت به اندازه کمی کندتر از $$n^2$$ رشد می‌کند. در نتیجه می‌توان گفت که $$n^2$$ کران بالا یا بیشترین محدوده سرعت رشد تابع $$100n^2 + n + 50$$ است. همچنین می‌توان گفت که:

$$n^2 = O(100n^2 + n + 50)$$

با استفاده از این فرمول‌ها می‌توانیم سرعت رشد توابع در ساختمان داده را در زمان کوتاهی مقایسه کنیم.

می‌‌توانیم بگوییم اگر دو مقدار ثابت $$c$$ و $$n_0 ≥ 0$$ وجود داشته باشند زمان اجرای تابع، الگوریتم یا برنامه برابر با $$O(f(n))$$ است. به طوری که برای همه ورودی‌هایی با اندازه $$n \ge n_0$$، زمان اجرا حداکثر برابر $$c f(n)$$ ثانیه می‌شود.

در تصویر نمودار زیر، توابع مختلف $$n$$ و $$10n+1200$$ و $$n^2$$ و $$n^2+5n+1000$$ و $$2^{0.1n}$$ را با استفاده از نماد $$O$$ بزرگ با یکدیگر مقایسه کرده‌ایم.

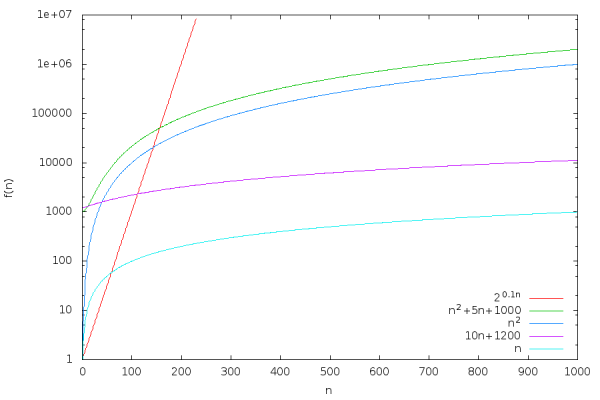
در فهرست زیر، نمودار بالا را تحلیل و توابع مختلف را با یکدیگر مقایسه کرده‌ایم.

• مقایسه $$n$$ و $$10n + 1200$$: در ابتدا به‌ازای مقادیر کوچک $$n$$ تفاوت بین این دو تابع بزرگ و قابل توجه است. اما هرچه که مقدار $$n$$ بیشتر می‌شود، فاصله بین این دو نمودار در مقیاس لگاریتمی کمتر شده است. این مسئله به معنای آن است که $$10n + 1200$$ فقط به مقدار ثابتی بزرگتر از $$n$$ است. برای مثال اگر $$n$$ برابر با ۵۰۰ باشد، محاسبات زیر برقرار است.

 $$\frac{10 \times 500 + 1200}{500} = \frac{5000 + 1200}{500} = 12$$

همچنین اگر مقدار $$n$$ خیلی بزرگ شود هم می‌توان از معادله زیر مقدار تفاوت این دو تابع را محاسبه کرد.

 $$\lim_{n \to \infty} \frac{n}{10n + 1200} = 10$$

محاسبات بالا نشان می‌دهد که عبارت $$10n + 1200 = O(n)$$ برقرار است. در نتیجه $$n$$ نرخ صحیح رشد برای هر دو تابع است.

توابع زیر هم از دید نماد $$O$$ بزرگ شبیه به یکدیگر هستند.

1. عبارت $$10n+1200=O(n)$$ برقرار است. زیرا به‌ازای تمام n-های بزرگتر مساوی ۵۰۰، عبارت $$10n+1200≤12n$$ برقرار است.
2. عبارت $$n=O(10n+1200)$$ هم بدیهی است.

بنابراین، در زمان مقایسه نرخ رشد توابع $$10n+1200$$ و $$n$$ می‌توان از $$n$$ به عنوان مقدار تقریبی استفاده کرد. در واقع $$n$$ تابع ساده‌تری است.

• مقایسه توابع $$n2$$ و $$n^2+5n+1000$$: در زمان مقایسه این دو تابع هم به نتیجه‌ای مانند نتیجه بالا می‌رسیم.
• مقایسه $$n$$ و $$n^2$$: در زمان مقایسه $$n$$ و $$n^2$$ می‌توان دید که فاصله بین این نمودارها دائما بزرگتر می‌شود. هرچه که $$n$$ بزرگتر شود، $$n^2$$ هم با سرعت بسیار بیشتری رشد می‌کند. یعنی اینکه سرعت رشد $$n^2$$ بیشتر از $$n$$ است.

 $$\lim_{n\to\infty}\frac{n^2}{n} = \infty$$

به طور کلی، توابع درجه دو - مانند $$n^2$$ - با سرعت بسیار بیشتری از توابع خطی - مانند $$n$$ - رشد می‌کنند. در زمان بررسی توابع چند جمله‌ای، در تعیین سرعت نرخ رشد فقط بیشترین توان اهمیت دارد.

• مقایسه توابع $$n^2$$ و $$2^{0.1n}$$: با مقایسه گرافیکی توابع $$n^2$$ و $$2^{0.1n}$$ می‌توان دید که تابع $$n^2$$ به‌ازای مقادیر کوچک $$n$$ به میزان قابل توجهی بزرگتر است. اما بعد از مقدار $$n$$ برابر با ۱۴۴، تابع $$2^{0.1n}$$ با سرعت بسیار بیشتری رشد می‌کند. از نگاه ریاضی سرعت رشد بیشتر تابع $$2^{0.1n}$$ نسبت به $$n^2$$ قابل اثبات است. اگر حد این تابع را در مقدار بی‌نهایت حساب کنیم، نتیجه زیر بدست می‌آید.

 $$\lim_{n \to \infty}\log\frac{2^{0.1n}}{n^2} = \lim_{n \to \infty}(0.1n - 2\log n) = \infty$$

در نتیجه تابع $$2^{0.1n}$$ بدون هیچ محدوده‌ای رشد می‌کند. اگر لگاریتم $$n$$ میل به بی‌نهایت کند، $$n$$ هم به سمت بی‌نهایت زیاد می‌‌شود. بنابراین $$2^{0.1n} \neq \mathcal{O}(n^2)$$ است. اما عبارت $$n^2 = O(2^{0.1n})$$ برقرار است. زیرا:

 $$\lim_{n \to \infty}\log\frac{n^2}{2^{0.1n}} = \lim_{n \to \infty}(2\log n - 0.1n) = -\infty$$

اگر لگاریتم $$n$$ میل به منفی بی‌نهایت کند، آن‌گاه مقدار $$n$$ به صفر نزدیک می‌شود. در نتیجه می‌توان چنین نتیجه گرفت که توابع نمایی با سرعت بیشتری نسبت به توابع چند جمله‌ای رشد می‌کنند.

دسته‌بندی O بزرگ برای توابع «قابل انتقال» (Transitive) است. به این معنا که اگر$$g$$ کران بالای تابع $$f$$ باشد و $$h$$ هم کران بالای تابع$$g$$ باشد در نتیجه $$h$$ کران بالای تابع $$f$$ هم هست.

در فرمول زیر شکل ریاضی این عبارت را نوشته‌ایم.

• لم:

اگر $$f(n)=O(g(n))$$ و $$g(n) = \mathcal{O}(h(n))$$ در نتیجه $$f(n) = \mathcal{O}(h(n))$$

دو علامت‌گذاری دیگر هم در ارتباط با نماد $$O$$ بزرگ وجود دارد.

• «اومگا بزرگ» (Big-Omega): این نماد کران پایین را نشان می‌دهد. به این صورت تعریف می‌شود که $$f(n) = \Omega(g(n))$$ است. اگر ثابت‌های $$n_0 \gt 0$$ و $$c \gt 0$$ وجود داشته باشند و برای تمام $$n \ge n_0$$ عبارت $$f(n) = \mathcal{O}(h(n))$$ برقرار باشد.
• «تتا بزرگ» (Big-Theta): این نماد کران دقیق را نشان می‌دهد. به این صورت می‌نویسیم که $$f(n) = \Theta(g(n))$$ برقرار است اگر هر دو عبارت $$f(n) = \mathcal{O}(g(n))$$ و $$f(n) = \Omega(g(n))$$ برقرار باشند.

رابطه بین O بزرگ و اومگا بزرگ واضح و ساده است.$$g$$ کران بالای $$f$$ است. اگر و تنها اگر $$f$$ کران پایین$$g$$ باشد.

• لم:

عبارت $$f(n) = \Theta(g(n))$$ برقرار است

اگر $$f(n) = \mathcal{O}(g(n))$$ آن‌گاه $$g(n) = \Omega(f(n))$$

به همین صورت اگر $$f(n) = \Omega(g(n))$$ آن‌گاه $$g(n) = \mathcal{O}(f(n))$$

برای مثال در بالا دیدیم که عبارت‌های زیر، برقرار هستند.

• $$n^2+5n+1000 = \Theta(n^2)$$
• $$2^{0.1n} = \Omega(n^2)$$
• $$n^2 = \Omega(n)$$

مشاهده می‌کنیم که در توابع نمایی حتی افزایش‌ کوچکی در توان تابع هم می‌تواند تغییر زیادی در نتیجه ایجاد کند. برای نمونه $$2^{0.1n}$$ و $$2^{n}$$ را مقایسه می‌کنیم. $$2^{0.1n} = \mathcal{O}(2^{n})$$ برقرار است. زیرا به‌ازای تمام $$n \ge 1$$ عبارت $$2^{0.1n} \le 2^{n}$$ برقرار است. اما $$2^{n} \neq \mathcal{O}(2^{0.1n})$$ زیرا نرخ $$\frac{2^{n}}{2^{0.1n}} = 2^{0.9n}$$ همزمان با زیاد شدن $$n$$ و بدون محدودیت افزایش پیدا می‌کند.

آموزش ساختمان داده توسط فرادرس

فرادرس به عنوان تولید کننده آنلاین محتوای آموزشی، همیشه تلاش کرده تا بهترین فیلم‌ها و مطالب را به شکل با کیفیت و بسیار کامل در اختیار مخاطبان خود قرار دهد. درس‌های مربوط به ساختمان داده تقریبا در همه زیرمجموعه‌های علوم کامپیوتر در دانشگاه‌ها تدریس می‌شوند. علاوه بر توسعه‌دهندگانی که می‌خواهند وارد دنیای حرفه‌ای تولید نرم‌افزار شوند، دانشجویان نیز باید برای موفقیت در تحصیل در این حوزه‌ها مطالعه کنند. فیلم‌های آموزشی فرادرس یکی از بهترین گزینه‌های برای تسلط بر روی دروس دانشگاه است.

تماشای فیلم‌های آموزشی فرادرس باعث کاهش هزینه‌ها، افزایش بهره‌وری و یادگیری بهتر می‌شود. وب‌سایت آموزشی فرادرس، فیلم‌های کاملی درباره درس‌های مربوط به ساختمان داده تولید کرده است. در فهرست پایین، چند مورد از این فیلم‌های آموزشی را معرفی کرده‌ایم.

• فیلم آموزش ساختمان داده ها به صورت جامع و با نکات مهم در فرادرس
• فیلم آموزش حل سوالات آزمون های استخدامی ساختمان داده در فرادرس
• فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java با فرادرس
• فیلم آموزش رابطه های بازگشتی در طراحی الگوریتم و ساختمان گسسته همراه با مرور و تست کنکور ارشد با فرادرس
• فیلم آموزش ساختمان داده درخت بازه ها Segment Tree و پیاده سازی آن در C++‎ با فرادرس

مشاهده فیلم‌های فرادرس برای اشخاص علاقه‌مند به استفاده کاربردی از علم نیز مفید است. زیرا این فیلم‌ها شامل مطالب کاربردی و مرتبط به پروژه‌های روز دنیا هستند. در صورت تمایل برای مشاهده فیلم‌های بیشتر درباره ساختمان داده بر روی تصویر بالا کلیک کنید.

بررسی و تحلیل عملیات ریاضی بر روی ماتریس ها

به منظور درک بهتر رشد توابع در ساختمان داده، نمونه‌ای از عملیات رایج بر روی ماتریس‌ها را بررسی می‌کنیم. عملیاتی بررسی شده در این بخش، شامل جمع و ضرب n ماتریس‌ مجزا از هم است.

بررسی جمع n ماتریس مختلف

برای شروع کار به بررسی روش جمع ماتریس‌ها پرداخته‌ایم.

می‌خواهیم ببینیم اجرای این متد براساس $$n$$ ماتریس مختلف چه مقدار طول می‌کشد. بررسی این متد ساده است. زیرا روش انجام کار شفاف بوده و از ساختار ساده‌ای پیروی می‌کند.

برای تحلیل ساده این مسئله باید به تمام کارهای مرحله‌به‌مرحله متد توجه کنیم. همچنین باید تعداد اجرای عملیات پایه را نیز بشماریم. به این منظور از متغیر رسمی $$tx$$ استفاده می‌کنیم.

در ابتدا متد مورد استفاده ماتریس جدیدی به نام «result» ایجاد می‌کند. یعنی اینکه به اندازه لازم برای ذخیره‌سازی شیء ماتریس جدید، حافظه تخصیص داده می‌شود. این حافظه به اندازه $$n \times n$$ داده ورودی است. اجرای این مرحله به مقدار $$t_{i,1}$$ زمان صرف می‌کند. سپس تمام ورودی‌های ماتریس را برابر با $$0.0$$ قرار می‌دهیم. زمان بخش مقداردهی هم به اندازه $$t_{i,1}+n^{2}t_{i,2}$$ طول می‌کشد. در این فرمول $$t_{i,2}$$ برابر با زمان مورد نیاز برای مقداردهی هر داده ورودی در آرایه است.

در مرحله بعد، متد از حلقه for  استفاده می‌کند. در این حلقه، متغیر سطر row، $$n$$ بار افزایش پیدا می‌کند. هربار افزایش متغیر row  به اندازه $$t_{l,1}$$ زمان نیاز دارد. متغیر ستون - با نام column  - هم به تعداد $$n \times n$$ بار افزایش پیدا می‌کند. زمان هربار افزایش متغیر column  برابر با $$t_{l,2}$$ است. بدنه حلقه به اندازه $$n \times n$$ بار اجرا می‌شود. هربار پیمایش حلقه هم به مقدار $$t_{l,3}$$ طول می‌کشد. بنابراین کل زمان مورد نیاز برای اجرای کامل حلقه برابر با $$nt_{l,1}+n^{2}(t_{l,2}+t_{l,3})$$ است.

در نهایت الگوریتم محاسبه result به اندازه $$t_{e}$$ طول می‌کشد. بنابراین زمان کل برابر است با:

$$t_{i,1}+n^{2}t_{i,2}+nt_{l,1}+n^{2}(t_{l,2}+t_{l,3})+t_{e}$$

تا به اینجای کار به فرمولی رسیده‌ایم که زمان مورد نیاز - یا تعداد عملیات پایه - را برای اجرای متد براساس $$n$$ پارامتر محاسبه می‌کند.

البته هنوز مقادیر دقیقی به‌ازای «متغیرهای زمان $$t_{x}$$» بدست نیاورده‌ایم. این متغیر‌ها وابسته به چندین پارامتر مختلف هستند. برای مثال می‌توان به موارد نوشته شده در فهرست زیر اشاره کرد.

• «سرعت کلاک» (Clock SpeeD) سخت‌افزارهایی مانند CPU و حافظه داخلی که در زمان اجرای کدها استفاده می‌شوند.
• میزان دقت «ریزمعماری» (Microarchitectural) و جزئیات پیکربندی سخت‌افزار
• میزان بهینه‌سازی «بایت کد» (Byte Code) که کامپایلر اسکالا انجام می‌دهد- یعنی اینکه کامپایلر «اسکالا» (Scala) مورد استفاده چقدر خوب کار می‌کند.
• سطح بهینه‌سازی مفسر «بایت کد» (Byte Code) - اشاره به «ماشین مجازی جاوا» ( Java Virtual Machine) مورد استفاده دارد.

با توجه به فهرست بالا، مشخص است که پیدا کردن مقادیر دقیق $$t_{x}$$ ساده نیست. پس به‌جای تلاش برای رسیدن به جواب دقیق باید جوابرا به صورت حدودی پیدا کنیم.

در نتیجه، مقدار حافظه متد و زمان محاسبه جواب در مقایسه با سایر بخش‌ها اهمیت کمتری دارند. مشخص است که برای ماتریسی به اندازه $$n$$ وقتی $$n$$ به مقدار کافی بزرگ باشد، مقداردهی ماتریس و بدنه حلقه for  بیشتر‌ از سایر بخش‌ها زمان می‌برد. هر دو این بخش‌ها $$n \times n$$ بار تکرار می‌شوند. به نظر می‌رسد که بیشترین زمان اجرای متد در این بخش‌ها صرف می‌‌شود. با توجه به این مسئله می‌توانیم بگوییم که زمان اجرای متد در حدود $$c_{1}n^{2}$$ است. در این فرمول، مقدار $$c_{1}$$ ثابت است.

«نماد $$O$$ بزرگ» (Big O Notation) را در بخش‌های بعدی معرفی می‌کنیم. این نماد کمک می‌کند تا دلیل اهمیت این ساده‌سازی تقریبی را درک کنیم. بخصوص وقتی که تمرکز اصلی ما بر روی مقیاس‌پذیری تابع یا الگوریتم است. در بخش بعدی درباره ضرب ماتریس‌ها هم مثالی را بررسی کرده‌ایم. 

بررسی ضرب n ماتریس مختلف

در این بخش تحلیل ساده‌ای بر روی کدهای مربوط به عملیات ضرب انجام داده‌ایم.

درونی‌ترین بخش حلقه‌ها در مثال بالا شامل عبارت v += this(row, i) * that(i, column) است. این بخش $$n^{3}$$ بار اجرا می‌شود. در حالی که سایر بخش‌های کد بالا در بیشترین حالت $$n^{2}$$ بار اجرا می‌‌شوند. در نتیجه به راحتی می‌توان حدس زد که زمان اجرای این متد به صورت تقریبی برابر با $$c_{2}n^{3}$$ است. در این فرمول هم آرگومان $$c_{2}$$ ثابت است.

قبل از پرداختن به ادامه بحث، باید ببینیم آیا این تخمین‌ها به مقادیر واقعی نزدیک هستند یا نه. برای بررسی این موضوع، مقادیری را به‌ازای ثابت‌های $$c_{2}$$ و $$c_{1}$$ انتخاب می‌کنیم. سپس بررسی می‌کنیم که تخمین‌های ما به‌ازای $$c_{2}n^{3}$$ و $$c_{1}n^{2}$$ چقدر با زمان واقعی اجرا به‌ازای $$n$$ همخوانی دارند.

فرض کنیم با توجه به سخت‌افزار و نرم‌افزار مورد استفاده، $$c_{2}$$ برابر با ۳۰ نانوثانیه و $$c_{1}$$ برابر با ۱۵ نانوثانیه است. سپس نتیجه حاصل از این تخمین‌ها را در کنار نتیجه حاصل از اجرای واقعی کدها محاسبه می‌کنیم. نتایج بدست‌ آمده را بر روی نمودار و در کنار هم رسم می‌کنیم. در تصویر زیر نتیجه این مقایسه را می‌توان مشاهده کرد.

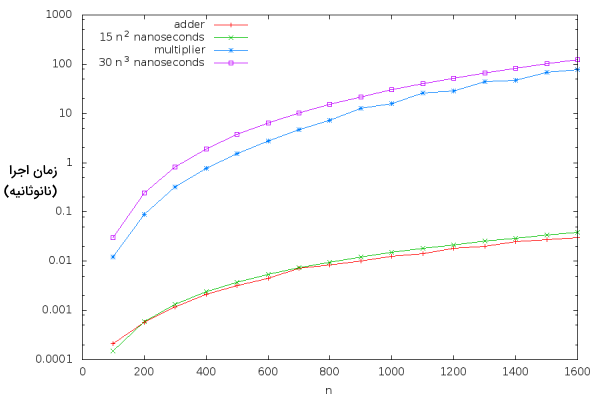
به نظر می‌رسد که تخمین‌های زده شده، نزدیک به نتایج واقعی هستند.

مثال‌هایی درباره رشد توابع در ساختمان داده

در این بخش از مطلب برای هر کدام از توابع رایج - توابع معرفی شده در اول مطلب - پیچیدگی زمانی $$O$$ بزرگ را بررسی کرده‌ایم.

عملیات ریاضی اولیه

در این بخش از مطلب، زمان‌ اجرای عملیات پایه را در ریاضی بررسی کرده‌ایم. عملیات پایه ریاضی مانند جمع، ضرب، عملیات بولی و غیره برای اجرا شدن بر روی انواع درونی، زمان ثابتی صرف می‌کنند. به عنوان مثال‌های از انواع درونی می‌توان به نوع Boolean، عدد صحیح و Double اشاره کرد.

فرض کنیم که x  و y  از نوع Double باشند، بنابراین عبارت‌های x + y  و x * y  را می‌‌توان در زمان ثابت محاسبه کرد. اما اگر هر کدام x  یا y  از نوع «BigInt» باشند، عملیات x + y  و x * y  در مدت زمان ثابت انجام نمی‌شود. نوع BigInt برای نگهداری مقادیر عدد صحیح بسیار بزرگ استفاده می‌‌شود.

به عنوان مثال، جمع کردن دو عدد $$n$$ بیتی، در کمترین حالت باید به اندازه $$\mathcal{O}(n)$$ زمان صرف کند. در زبان برنامه نویسی Scala - و بسیاری دیگر از زبان‌های برنامه نویسی مدرن - می‌توان عملگرها را «Overload» کرد. در نتیجه در زمان خواندن کدها باید به این نوع از مسائل دقت کنیم. زیرا عملگرهای به ظاهر ساده‌ای مانند ضرب «*» ممکن است که زمان بسیار طولانی برای انجام محاسبات صرف کنند.

آرایه هایی با دسترسی تصادفی

در این بخش به بررسی زمان‌ ثابت $$O(1)$$ در عملیات بر روی آرایه‌هایی با دسترسی تصادفی پرداخته‌ایم. برای اینکه در آرایه «$$arr$$» به عنصر موجود در اندیس «$$i$$» دسترسی داشته باشیم، از عبارت «$$arr(i)$$» استفاده می‌کنیم. این عملیات در زمان ثابت انجام می‌‌شود. از آنجا که آرایه‌ها در اصل توسط ماشین مجازی سطح پایین و سخت‌افزار پشتیبانی می‌شوند. در نتیجه دسترسی به خانه‌های آرایه در زمان ثابت $$O(1)$$ انجام می‌‌شود.

در مقابل، اگر شیء لیستی به نام $$l$$ داشته باشیم، عملیات دسترسی به عنصر $$l(i)$$ در زمان ثابت انجام نمی‌شود. این مسئله به خاطر آن است که ساختار لیست طوری طراحی شده که برای دسترسی به عنصر $$i$$ در بدترین حالت ممکن باید $$O(n)$$ عنصر - در لیست با طول $$n$$ - پیمایش شوند.

 پیدا کردن عنصر مشخصی در داده‌‌های نامرتب

عملیات پیدا کردن عنصر مشخص در میان داده‌‌های نامرتب در زمان خطی $$O(n)$$ انجام می‌شود. فرض کنیم که آرایه «$$arr$$» را با «$$n$$» عدد صحیح در اختیار داریم. تمام اعداد موجود در آرایه به شکل نامرتبی قرار گرفته‌اند. در این حالت پیدا کردن عدد صحیح x  در آرایه - برای مثال با استفاده از تابع arr.contains(x)  - به اندازه $$O(n)$$ زمان صرف می‌کند. در بدترین حالت اصلا عدد x  در آرایه وجود ندارد. برای فهمیدن این مسئله مجبوریم که x  را با تمام عناصر درون آرایه مقایسه کنیم. هربار انجام مقایسه در آرایه‌ها، زمان ثابتی به اندازه $$O(1)$$ صرف می‌کند. در بهترین حالت هم عدد x  اولین عنصر قرار گرفته در آرایه است. بنابراین کران پایین زمان اجرای این عملیات برابر با $$Ω(1)$$ است.

البته اگر اعداد صحیح درون آرایه به صورت مرتبی قرار گرفته باشند، وضعیت تفاوت کرده و عنصر مورد نظر در زمان ثابت پیدا می‌شود.

مرتب‌سازی درجی

عملیات مرتب سازی درجی وظیفه خود را در زمان مربع $$n$$ یعنی $$\mathcal{O}(n^2)$$ اجرا می‌کند. فرض کنیم که آرایه‌ای از اعداد صحیح در اختیار داریم. باید عناصر این آرایه را با ترتیب صعودی مرتب کنیم. برای مثال می‌خواهیم که آرایه (4, -3, 3, 2, 1, -2) را به آرایه (-3, -2, 1, 2, 3, 4)  تبدیل کنیم. به الگوریتم‌هایی که برای انجام این وظیفه استفاده می‌‌شوند، الگوریتم‌های مرتب سازی گفته می‌‌شود. برای آشنایی با این الگوریتم‌ها می‌توانید مطلب مرتبط با آن را در مجله فرادرس مطالعه کنید.

یکی از ساده‌ترین روش‌های مرتب‌سازی، «الگوریتم مرتب‌سازی درجی» (Insertion Sort Algorithm) است. این الگوریتم با روش زیر کار می‌کند.

• به‌ازای تمام موقعیت‌هایi  از ۰ تا n-1  در آرایه، الگوریتم به دنبال عنصر x  در موقعیت i  می‌گردد.
• عنصر x  را با عنصر موجود در موقعیت i  مقایسه می‌کند.
• هر کدام که کوچک‌تر بودند به ابتدای آرایه منتقل می‌شوند. در واقع موقعیت قرارگیری این عناصر با یکدیگر جابه‌جا می‌شود.
• بعد از بررسی موقعیت i  می‌توان نتیجه گرفت که i+1  عنصر اول مرتب شده‌اند.
• بعد از هربار پیمایش، مقدار i  به اندازه یک واحد افزایش پیدا می‌کند.
• بعد از اینکه i=n-1  هم بررسی شد، تمام عناصر آرایه مرتب شده‌اند.

در زبان برنامه نویسی اسکالا، می‌توانیم الگوریتم مرتب‌سازی درجی را به روش زیر پیاده‌سازی کنیم.

سپس در کنسول Scala تابع را به صورت زیر اجرا می‌کنیم.

تحلیل پیچیدگی زمانی الگوریتم مرتب‌سازی درجی

مقدار پیچیدگی زمانی الگوریتم‌های مرتب سازی با یکدیگر تفاوت دارند. در این بخش از مطلب، پیچیدگی زمانی الگوریتم مرتب‌سازی درجی را تحلیل کرده‌ایم.

1. اگر آرایه‌ای با $$n$$ عدد صحیح داشته باشیم، حلقه for  باید $$n$$ بار اجرا شود.
2. در پیمایش شماره i  هم حلقه while  در بیشترین حالت به اندازه $$n$$ بار اجرا می‌شود.
3. بقیه عملیات‌ها در مدت زمان ثابتی اجرا می‌شوند.
4. بنابراین کل زمان اجرای این الگوریتم برابر با $$\mathcal{O}(\frac{n(n-1)}{2}) = \mathcal{O}(n^2)$$ است.

حالت بهینه اجرای این الگوریتم برای کسب کوتاه‌ترین زمان، مربوط به وقتی است که آرایه از قبل مرتب شده است. در این صورت با هر دفعه پیمایش‌ حلقه for، بدنه حلقه while  فقط یکبار اجرا می‌شود. بنابراین مدت زمان اجرای الگوریتم به کران پایین $$\Omega(n)$$ نزدیک است.

الگوریتم‌های مرتب‌سازی مختلفی با ویژگی‌های متفاوت وجود دارند. در زبان اسکالا متد sorted  در Seq  از تکنیک مرتب‌سازی براساس کلاس آرایه‌های زبان جاوا استفاده می‌کند. پیچیدگی زمانی اجرای این الگوریتم مرتب‌سازی برابر با $$\mathcal{O}(n \log n)$$ است. این مسئله به شرطی درست است که مقایسه دو عنصر به اندازه زمان ثابتی طول بکشد.

ضرب ماتریسی

در بخش‌های بالاتر همین مطلب متوجه شدیم که «پیچیدگی زمانی عملیات ضرب ماتریسی» برابر با مکعبی از $$n$$ - ابعاد ماتریس - یا $$\mathcal{O}(n^3)$$ است. $$n$$ نشان دهنده مقدار فضای اشغال شده توسط ماتریس نیست. پیچیدگی فضایی ماتریسی $$n$$ بُعدی برابر با $$\mathcal{O}(n^2)$$ است. از آنجا که الگوریتم مورد استفاده در این مطلب شامل هیچ شرطی نیست، بهترین حالت عملکرد آن با بدترین حالت آن برابر هستند. یعنی آنکه زمان اجرا با کران پایین $$\Omega(n^3)$$ و «کران دقیق» (Exact Bound) «$$\Theta(n^3)$$» خود، برابر است.

نکته: برای ضرب دو ماتریس، الگوریتم‌های سریع‌تری هم شناخته شده‌اند. به عنوان مثال می‌توان به «الگوریتم استراسن» (Strassen Algorithm) و «الگوریتم لِ گال» (Le Gall’s algorithm) اشاره کرد.

مربع‌سازی تکراری با دقت دلخواه

انجام عملیات «مربع‌سازی تکراری» (Iterative Squaring) با «دقت دلخواه» (Arbitrary Precision) پیچیدگی زمانی با مقدار نمایی دارد. برای درک بهتر این مطلب ابتدا به کد زیر توجه کنید.

در کدهای بالا تابع f(n)  عدد $$2^{2^n}$$ را محاسبه می‌کند. نمایش باینری جواب این تابع نیاز به $$2^n$$ بیت دارد. به غیر از این مطلب، خود کد هم حلقه‌ای دارد که باید به اندازه $$n$$ بار پیمایش شود. زمان اجرای این حلقه برابر با $$\Omega(2^n)$$ است. زیرا با هربار اجرای خط کد result = result * result اندازه نتیجه یا result  دوبرابر می‌شود. توجه کنید که مقدار result  به شکل باینری ذخیره می‌شود. در ضمن، ضرب دو عدد با i  تعداد بیت به اندازه $$\Omega(i)$$ زمان صرف می‌کند.

پیمایش تمام جایگشت‌ها

زمان اجرای عملیات مربوط به پیمایش تمام جایگشت‌ها با نماد فاکتوریل نمایش داده می‌شود. جایگشت مجموعه‌ای از اشیا به روش چیدمان آن اشیا به ترتیب خاصی گفته می‌شود. برای نمونه اگر اشیا a  و b  و c  را داشته باشیم. می‌توان گفت("a","b","c") و ("c","b","a") دو جایگشت مختلف از این اشیاء هستند. به طول کلی چنین می‌‌توان گفت که اگر مجموعه‌ای از $$n$$ شی‌ء مجزا از هم داشته باشیم، آن‌گاه $$n!$$ جایگشت مجزا از این اشیاء وجود دارد.

در زبان اسکالا، متدی به نام permutations تعریف شده است. از این متد برای محاسبه جایگشت‌ عناصر کلاس‌هایی مانند List  و ArrayBuffer استفاده می‌شود. با کمک این متد می‌‌توان بر روی تمام جایگشت‌های عناصر موجود در توالی مورد نظر پیمایش کرد.

برای نمونه در کد زیر، مثالی را بررسی کرده‌ایم.

می‌دانیم که برای هر مجموعه شامل $$n$$ عنصر، $$n!$$ هم جایگشت مختلف وجود دارد. تولید هر جایگشت، در کمترین حالت به مقدار $$\Omega(1)$$ زمان صرف می‌کند. در نتیجه پیمایش بر روی تمام جایگشت‌ها به زمانی معادل $$\Omega(n!)$$ نیاز دارد.

یادگیری طراحی الگوریتم و ساختمان داده با کمک فرادرس

بسیار مهم است که به عنوان برنامه‌نویس، با طراحی الگوریتم نیز آشنا باشیم. توانایی اندازه‌گیری و بهینه‌سازی رشد توابع در ساختمان داده یکی از بخش‌های تخصصی در الگوریتم نویسی است. فرادرس به عنوان تولید کننده محتوای آنلاین آموزشی تمرکز زیادی بر روی تولید و انتشار فیلم‌های آموزش طراحی الگوریتم کرده است. بعضی از این فیلم‌ها با رویکرد کسب آمادگی برای شرکت در آزمون‌های دانشگاهی تولید شده‌اند. طراحی و نوشتن الگوریتم رابطه‌ بسیار نزدیکی با برنامه‌نویسی و ساختمان داده‌ دارند. در قسمت پایین، چند مورد از فیلم‌ها آموزشی فرادرس درباره طراحی الگوریتم و ساختمان داده را معرفی کرده‌ایم.

• فیلم آموزش طراحی الگوریتم به صورت جامع و با مفاهیم کلیدی در فرادرس
• فیلم آموزش حل سوالات آزمون های استخدامی طراحی الگوریتم با فرادرس
• فیلم آموزش طراحی الگوریتم همراه با حل مثال های عملی در فرادرس
• فیلم آموزش طراحی الگوریتم، مرور و تست کنکور ارشد با فرادرس
• فیلم آموزش روش تقسیم و حل در طراحی الگوریتم، مرور و تست کنکور کارشناسی ارشد در فرادرس

مهارت در حل مسائل مربوط به این حوزه یکی از توانایی‌های لازم برنامه‌نویسان و مهندسان حرفه‌ای نرم‌افزار است. با کلیک بر روی تصویر زیر می‌توانید وارد صفحه اصلی این مجموعه آموزشی شده و از فیلم‌های بیشتری دیدن کنید.

اهمیت ثابت ها در ضرب ماتریس ها

وقتی که درباره مقیاس‌پذیری و نماد $$O$$ بزرگ صحبت می‌کردیم، ثابت‌ها را از محاسبات خود کنار گذاشتیم. اما در زمان بهینه‌سازی کدها برای رسیدن به بهترین نتیجه ممکن، باید به ثابت‌ها هم توجه کنیم.

برای درک بهتر این مطلب، ابتدا به کدهای مربوط به ضرب ماتریس‌ها به عنوان مثالی توجه کنید.

نکته: بهینه‌سازی‌ها کدها اغلب اوقات خوانایی آن‌ها را کم‌تر می‌کند. هدف اصلی از اینکار سریع‌تر ساختن اجرای الگوریتم است. در نتیجه فقط باید آن بخش از کدها را بهینه‌سازی کنیم که واقعا از نظر عملکرد اهمیت دارند.

بهینه‌سازی کدها

در این قسمت، چند بهینه‌سازی مختلف بر روی کدهای برنامه انجام داده‌ایم. سپس میزان سریع‌تر شدن کدها را در عمل بررسی کردیم.

در ابتدا به بهینه‌سازی حلقه‌های for  می‌پردازیم. کامپایلر اسکالا تمام حلقه‌های for  را به صورت خودکار به متد foreach  تبدیل می‌کند. برای مثال، حلقه for  نوشته شده در کادر زیر:

تقریبا به کدهای نوشته شده در پایین ترجمه می‌شود.

شاید این مسئله بی‌اهمیت به نظر برسد. اما در واقع به معنی آن است که به‌ازای هر i، متد از فراخوانی تابع خاصی برای انجام محاسبات i => v += this(row, i) * that(i, column) استفاده می‌کند. نکته اینجا است که فراخوانی متدها هزینه بسیار بیشتری نسبت به انجام صرف توابع ریاضی و ارسال جواب به خروجی دارد. در نتیجه برای سریع‌تر اجرا شدن کدها، می‌توانیم حلقه‌های for  را با حلقه‌های while  جابه‌جا کنیم. زیرا حلقه‌های while  به متد foreach  تبدیل نمی‌شوند.

در تصویر زیر، نموداری را برای مقایسه زمان اجرای کدهای بالا مشاهده می‌کنید. هر دو خط زمان اجرای برنامه را بر اساس مقدار داده‌های ورودی به صورت نانوثانیه نشان می‌دهند. در خط قرمز از حلقه for  استفاده شده است و در خط سبز از حلقه while.

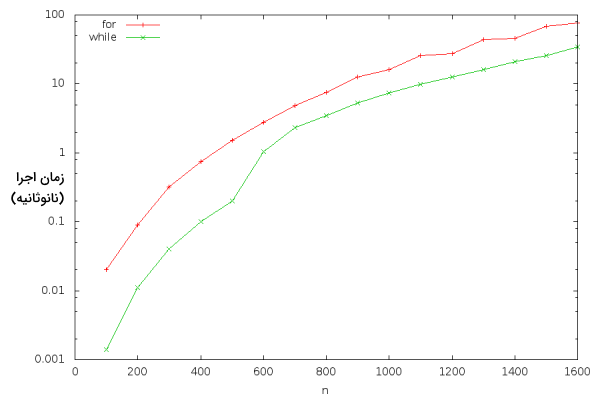
نکته خوب اینجاست که اولین روش ارتقای کدها هم نتیجه خوبی داشته و هم علی رغم طولانی‌تر شدن کد، خوانایی آن را کاهش نداده است.

با مشاهده نمودار بالا، می‌بینیم که عملکرد کد جدید هم در حدود $$n=600$$ با شیب تند‌تری زیاد شده است. این مسئله به خواطر آن اتفاق افتاد که ماتریس‌های «A» و «B» شروع کردند به پر کردن کش «L3» در CPU. کش «L3» حافظه‌ای سریع و کوچک است.

همچنین پهنای باند حافظه اصلی یکی دیگر از مشکلات است. این مشکل می‌تواند عملکرد کلی سیستم را کاهش دهد. در زمان اجرای پردازش‌های پیچیده و بزرگ، ممکن است CPU به مقدار داده بیشتری از توان ذخیره‌سازی کش‌ها نیاز داشته باشد. در این صورت، نیاز خود را از حافظه اصلی - که نسبت به کش کند‌تر است - تامین می‌کند. برای کاهش این مشکل، بهتر است داده‌ها را در آدرس‌های متوالی حافظه ذخیره کنیم. زیرا ذخیره داده‌ها در آدرس‌های متوالی باعث استفاده بهینه از حافظه می‌شود.

حافظه اصلی داده‌ها را به شکل کَش‌لاین‌های ۵۱۲ بیتی ارسال می‌کند. در واقع هر کَش‌لاین شامل ۸ کلمه متوالی ۶۴ بیتی است. برای اجرای بهترین بهینه‌سازی ممکن بر روی پهنای باند، باید تمام ۸ کلمه‌ای که از حافظه به CPU ارسال می‌شوند - به‌جای فقط یک کلمه در هر تراکنش - را به کار ببریم.

این مسئله زمانی اتفاق می‌افتد که از خانه‌های حافظه به صورت متوالی و پشت سر هم استفاده کنیم. در صورت استفاده نامنظم از خانه‌های حافظه - با حداقل ۸ گام فاصله بین این خانه‌ها - کارایی مورد نظر خود را بدست نمیاوریم.

اکنون دوباره کدها را بررسی کرده و نکته‌ای را که آموخته‌ایم، به کار می‌بریم. حلقه درونی به ماتریس A «this» دسترسی دارد. روش دسترسی به صورتی است که از کلمات متوالی ذخیره شده در آرایه استفاده می‌شود، پس این حلقه، عملکرد بهینه‌ای داشته و مشکلی ایجاد نمی‌کند.

اما عناصر ماتریس ‌B «that » به شکل دیگری استفاده می‌شوند. زیرا عناصر that(i,column)  و that(i+1,column)  پشت سر همدیگر قرار ندارند. زیرا عناصر موجود در این ماتریس خودشان آرایه‌های سطح پایین هستند.

برای حل این مشکل از ترفندی غیرمنتظره استفاده کرده‌ایم. قبل از انجام عملیات ضرب، جای سطر و ستون ماتریس ‌‌‌‌‌‌‌B را عوض می‌کنیم. در واقع از ترانهاده این ماتریس استفاده کرده‌ایم. این کار باعث می‌شود عناصر مورد استفاده در حلقه درونی یا همان ماتریس B، به صورت متوالی در حافظه قرار بگیرند. در نتیجه، عملکرد کلی برنامه بهبود می‌یابد.

در تصویر زیر، نموداری از عملکرد نسخه‌‌های مختلف و بهینه‌سازی شده برنامه ضرب ماتریس‌ها را نمایش داده‌ایم. با کمک این نمودار به خوبی می‌توان کیفیت عملکرد این کدها را با یکدیگر مقایسه کرد. سه خط قرمز، سبز و آبی زمان اجرای برنامه را بر اساس مقدار داده‌های ورودی به صورت نانوثانیه نشان می‌دهند. خط بنفش هم مقدار $$n^3$$ را نشان می‌دهد. در خط قرمز از حلقه for  استفاده شده است و در خط سبز از حلقه while. خط آبی نشان‌دهنده کدهایی است که هم از حلقه while استفاده کرده‌اند و ماتریس B در آن‌ها ترانهاده شده است.

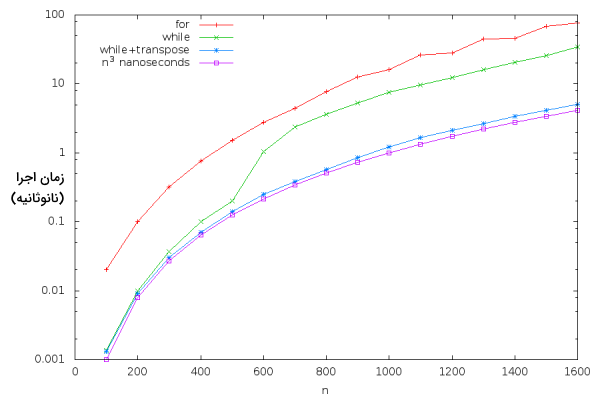
مشاهده می‌کنید با استفاده از ترفند ضرب ماتریس‌های ترانهاده، به سرعتی در حدود ۱۰ تا ۳۰ برابر سریع‌تر نسبت به پیاده‌سازی اولیه کدهای همان الگوریتم رسیده‌ایم.

در ضمن برای توضیح بیشتر، نمودار مربوط به تابع $$n^3$$ را هم در مقیاس نانوثانیه رسم کرده‌ایم. سرعت کلاک پردازنده سیستم مورد استفاده ۳٫۱ گیگاهرتز است. به این معنا که در هر نانوثانیه ۳٫۱ چرخه کلاک اجرا می‌شوند. از آنجا که ضرب ماتریس‌های $$n × n$$ نیازمنده اجرای $$n^3$$ عملیات ضرب با نوع Double است، آخرین نسخه الگوریتم بهینه‌سازی‌ شده در مطلب، نزدیک به بهترین حالت قابل پیاده‌سازی در زبان اسکالا است.

البته هنوز هم می‌توان سرعت اجرای این برنامه را بالا برد. در فهرست زیر دو مورد از روش‌های اینکار را بیان کرده‌ایم.

• الگوریتم را بر روی CPU-های چند هسته‌ای با توان اجرای پردازش موازی اجرا کنیم.
• استفاده از تکنولوژی «بردارسازی» (Vectorization)، البته به شرطی که توسط «ریزمعماری» (Microarchitecture) پردازنده پشتیبانی شود.

البته بهینه‌سازی‌های بیشتر ممکن است که باعث شود خوانایی، قابلیت نگهداری و جابه‌جایی کدها کاهش پیدا کنند.

نکته: بهینه‌سازی کدها وقتی مفید است که عملیات خاصی میلیاردها بار انجام شود. اما قبل از آن باید بررسی کنیم که آیا الگوریتم نوشته شده، همین‌ الان بهترین نسخه ممکن برای حل مسئله است یا نه. مانند مقایسه کردن مقیاس‌پذیری خطی و نمایی. از آنجا که بهینه‌سازی، خوانایی و قابلیت نگهداری کدها را کاهش می‌دهد، فقط بر روی بخش‌هایی تمرکز کنید که واقعا به بهینه‌سازی نیاز دارند. در صورت امکان از ابزارهای نظارتی برای پیدا کردن بخش‌هایی از کد استفاده کنید که بیشترین زمان در آنجا صرف می‌شود.

در صورتی که بخواهید کدهای خود را به بیشترین سرعت ممکن برسانید، باید اطلاعات زیادی درباره CPU و حافظه اصلی کامپیوتر داشته باشید.

جمع‌بندی

توجه به رشد توابع در ساختمان داده برای اجرای بهینه نرم‌افزارهای بزرگ از اهمیت زیادی برخوردار است. معمولا مقدار رشد تابع، رابطه مستقیمی با تعداد پارامتر ارسال شده به آن دارد. در صورت بی‌توجهی به استفاده از الگوریتم‌های صحیح و بهینه ممکن است کارایی سیستم در مقابل حجم داد‌ه‌های ورودی زیاد به شدت کند شده یا به طور کل متوقف شود. توسعه‌دهندگان حرفه‌ای که بر روی محصولات و پروژه‌های بزرگ کار می‌کنند، همیشه به این مسئله توجه دارند. برای نشان دادن معیار رشد توابع در ساختمان داده از نماد $$O$$ بزرگ استفاده می‌‌شود.

در این مطلب از مجله فرادرس ابتدا رشد تابع را تعریف کرده و سپس توابع مختلف را براساس نرخ رشد معرفی کردیم. درباره نماد $$O$$ بزرگ و روش محاسبه آن توضیحات کاملی را ارائه داده‌ایم. در نهایت هم درباره اهمیت ثابت‌ها و روش‌های بهینه‌سازی کدها مطالب مفیدی را ارائه کردیم.