خطای مشاهداتی در آمار – مفاهیم و انواع آن

علم مهندسی، به اندازه‌گیری و محاسبات مرتبط است. در این میان مقادیر اندازه‌گیری شده ممکن است دقیق نباشند. از طرفی با تکرار اندازه‌گیری نیز مقدارهای متفاوتی بدست می‌آید، زیرا عوامل و شرایط مختلفی روی دستگاه‌های اندازه‌گیری و همینطور افراد ناظر بر اندازه‌گیری تاثیر گذار هستند. از آنجایی که بعضی از عوامل موثر بر خطای اندازه‌گیری، تصادفی بوده و دارای توزیع احتمالی هستند، در این نوشتار به خطای مشاهداتی در آمار نیز پرداخته‌ایم تا با توجه به توزیع احتمال برای خطای تصادفی، میزان خطا را بطور مناسب حدس بزنیم.

برای آشنایی بیشتر با روش‌های اندازه‌گیری خطا نوشتارهای خطای اندازه گیری — به زبان ساده و دقت و صحت اندازه گیری – به زبان ساده را مطالعه کنید. همچنین خواندن مطلب‌های نماد علمی — به زبان ساده و موازنه واریانس و اریبی --- به زبان ساده نیز خالی از لطف نیست.

خطای مشاهداتی در آمار

معمولا در علوم مهندسی، فیزیک و شیمی، «خطای مشاهداتی» (Observational Error) یا «خطای اندازه‌گیری» (Measurement Error) به معنی اختلاف بین مقدار اندازه‌گیری شده و مقدار واقعی در نظر گرفته می‌شود. ولی در آمار، خطا به عنوان فقط یک اشتباه در انداز‌ه‌گیری محسوب نمی‌شود. تغییرات و خطا در اندازه‌گیری پدیده‌های تصادفی، در ذات آن‌ها قرار دارد. در غیر اینصورت دیگر چنین اتفاقاتی را تصادفی در نظر نمی‌گرفتیم.

فیلم آموزش درس رگرسیون 2 – جامع و کاربردی در فرادرس

کلیک کنید

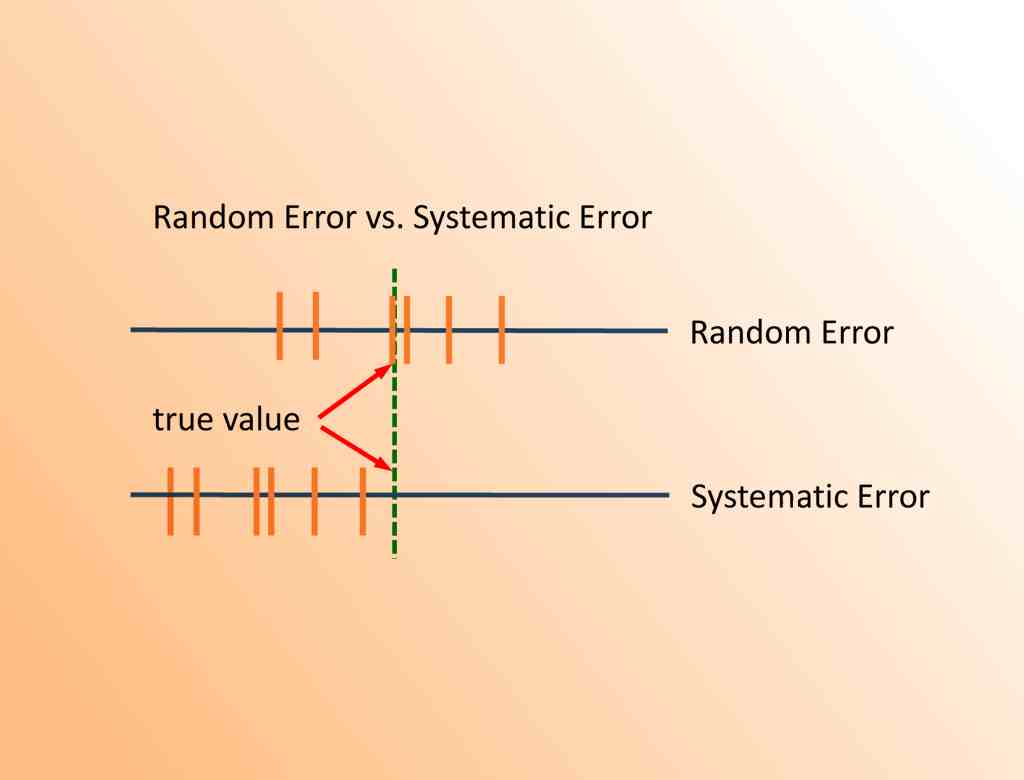
به این ترتیب خطاهای مشاهداتی در آمار را به دو بخش تقسیم می‌کنند. گروه اول مربوط به «خطاهای تصادفی» (Random Error) و گروه دوم نیز «خطاهای سیستماتیک» (Systematic Error) نامیده می‌شوند.

• خطای تصادفی: اگر عمل اندازه‌گیری را چندین بار تکرار کنیم، خطای حاصل از این عملیات را خطای تصادفی می‌نامند. زیرا شرایط و عوامل موثر بر اندازه‌گیری باعث ناسازگاری ثبت مقدار صحیح برای یک کمیت می‌شود.
• خطای سیستماتیک: خطاهایی که ناشی از تصادف نبوده و بستگی به ابزارهای سنجش یا فرآیند اندازه‌گیری دارند، خطای سیستماتیک نامیده می‌شوند. به این ترتیب خطای سیستماتیک، در ذات روش یا سیستم اندازه‌گیری نهفته است.

معمولا برای کاهش خطای تصادفی، از مقادیر خطا، میانگین گرفته می‌شود. با توجه به فرض صفر بودن میانگین خطای تصادفی، انتظار داریم میانگین مشاهدات نیز خطای تصادفی کمتری نسبت به هر یک از مشاهدات داشته باشند. ولی خطای سیستمی، معمولا دارای میانگین صفر نیست. در نتیجه با تکرار عمل اندازه‌گیری و محاسبه میانگین‌، اثر خطای سیستمی کاهش پیدا نمی‌کند.

آزمایش تجربی و علم

هر بار یک آزمایش تجربی را تکرار می‌کنیم، نتایج حاصل با تغییرات بسیار اندکی نسبت به یکدیگر حاصل می‌شوند. مدل‌های مختلفی برای توصیف خطاهای تصادفی در «نظریه آمار» (Statistical Theory) وجود دارد. معمولا خطای مشاهداتی در آمار را ناشی از دو بخش می‌دانند. همانطور که گفته شد، بخش اول خطای تصادفی است که از یک مشاهده به مشاهده دیگر متفاوت است. بخش دوم نیز خطای سیستماتیک است که معمولا میزان یا مقدار ثابتی داشته که بستگی به ابزار اندازه‌گیری یا شیوه به کارگیری آن دارد.

واضح است که خطای تصادفی (Random Error) یا تغییرات تصادفی (Random Variation) بستگی به عواملی دارند که نمی‌توان آن‌ها را کنترل کرد یا ثابت در نظر گرفت. یکی از دلایل وجود چنین خطاهایی، هزینه‌های زیاد برای ایجاد شرایط یکسان و کنترل شده یا امکان ناپذیری ایجاد محیط‌های ایده‌آل برای انجام آزمایشات علمی است. البته ممکن است ویژگی‌های پدیده‌ای که باید اندازه‌گیری شوند، دستخوش تغییر شوند، در نتیجه وجود مدل‌های دینامیک آماری که براساس توزیع‌های آماری و احتمالاتی ایجاد می‌شوند (مانند مکانیک کوانتمی) ضروری به نظر می‌رسد.

حتی ممکن است خطای تصادفی، با توجه به محدوده اندازه‌گیری دستگاه‌ها نیز حاصل شود. بطور معمول برای ثبت یک مقدار آخرین رقم‌های اعشار را گرد می‌کنند. با توجه به بزرگتر یا کوچکتر بودن آن رقم نسبت به ۵، عدد به بالا یا به پایین گرد می‌شود. در نتیجه  ممکن است سه مقدار متفاوت زیر برای نمایش یک مقدار واحد به کار رود. با توجه به اینکه شانس بزرگتر یا کوچکتر بودن یک رقم از ۵، تقریبا ۵۰٪ است، گرد کردن اعداد باعث خطای تصادفی با «توزیع دوجمله‌ای» (Binomial Distribution) می‌شود که پارامترهای آن، $$n$$ یا تعداد آزمایش‌ها و $$p=0.5$$ یا احتمال موفقیت است.

$$\large 0.9110\; \; \text{gr}, \;\; 0.9111\; \; \text{gr}, \;\; 0.9112 \;\;\text{gr}$$

گاهی خطای سیستماتیک را خطای سیستمی یا «اریبی آماری» (Statistical Bias) می‌نامند. این گونه خطاها را با استفاده از فرآیندهای استاندارد‌سازی (مانند کالیبره کردن) می‌توان کاهش داد. به همین علت در علوم مهندسی و پایه، بخشی از کلاس‌های درسی و آموزش‌ها دانشگاهی به کالیبراسیون ابزارها و روش‌های اندازه‌گیری به منظور کاهش خطای سیستماتیک اختصاص دارد.

خطای مشاهداتی در آمار: تصادفی در مقابل سیستماتیک

با توجه به تعریفی که برای خطای سیستمی و خطای تصادفی در حیطه خطاهای مشاهداتی در آمار ارائه کردیم، می‌توانیم گزاره‌های زیر را برای خطای سیستماتیک در نظر بگیریم:

• خطای مشاهداتی سیستماتیک قابل پیش‌بینی است.
• میزان خطای مشاهداتی سیستماتیک ثابت یا متناسب با مقدار واقعی است و معمولا به صورت درصدی از مقدار واقعی در نظر گرفته می‌شود.
• اگر منبع اصلی خطای سیستماتیک شناسایی شود، می‌توان مقدار آن را حذف یا به میزان حداقل کاهش داد.
• در بیشتر مواقع، کالیبراسیون نادرست می‌تواند علت اصلی خطای سیستماتیک باشد.
• شیوه ثبت یا مشاهده ناظر بر اندازه‌گیری می‌تواند خطای مشاهداتی سیستماتیک ایجاد کند.

در سال 2005 آزمون تصادفی (Test Uncertainty) طبق استاندارد PTC یا (Performance Test Standard) توسط بنیاد آمریکایی «مهندسین مکانیک» (American Society of Mechanical Engineers) که به اختصار ASME، نامیده می‌شود، ایجاد شد. در این آیین نامه، در مورد خطای تصادفی و سیستماتیک، به طور مفصل صحبت شده است. این دستورالعمل را می‌توانید با کلیک روی این لینک (+)، دریافت کنید.

در حقیقت در این متن اشاره می‌شود که تغییرات غیرقابل پیش‌بینی، خطاهای تصادفی نامیده شده که ناشی از محیط اندازه‌گیری یا ابزارها آن تحت شرایط متفاوت یا غیر ایده‌آل است. خطای تصادفی در ارتباط مستقیم با دقت اندازه‌گیری است. هر چه قدر دقت اندازه‌گیری افزایش یابد، میزان تغییرات (انحراف معیار) کاهش خواهد یافت.

در عوض خطای تصادفی ویژگی‌هایی مجزایی نسبت به خطای سیستمی دارد که آن‌ها را در ادامه، فهرست کرده‌ایم.

• خطای تصادفی همیشه در اندازه‌گیری‌ها، حضور دارد. زیرا مشاهده و ثبت مقادیر بطور ذاتی خطا به همراه دارند.
• با هر بار تکرار آزمایش و اندازه‌گیری، نتایج حاصل به واسطه وجود خطای تصادفی، متفاوت است. این وضعیت برعکس خطای سیستماتیک است که همیشه ثابت در نظر گرفته می‌شود.
• مقدار خطای تصادفی، قابل برآورد بوسیله تکرار عمل اندازه‌گیری است. معمولا از میانگین مقادیر خطا، به عنوان برآورد خطای تصادفی استفاده می‌شود.

منابع خطای تصادفی

خطای اتفاقی (Stochastic) یا تصادفی (Random) در اندازه‌گیری، خطایی است که از یک اندازه به اندازه‌گیری بعدی متفاوت است. معمولا توزیع احتمالی مقادیر خطای تصادفی را نرمال (Normal Distribution) فرض می‌کنند. این موضوع می‌تواند به علت قضیه حد مرکزی (Central Limit Theorem) باشد که تابع توزیع مجموعه خطاهای تصادفی مستقل با میانگین و واریانس ثابت را توزیع نرمال در نظر می‌گیرد. از طرفی خصوصیات این توزیع نسبت به توزیع‌های دیگر، شناخته‌ شده‌تر و ساده‌تر هستند.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

برای مثال در یک مدل رگرسیونی (Regression Model)، اگر مقادیر متغیر وابسته (Dependent Variable) براساس خطای تصادفی، اندازه‌گیری شوند، روی مدل و فرضیات اصلی مدل تاثیری نخواهند داشت بلکه میزان «ضریب تعیین» (Coefficient of determination) یعنی $$R^2$$ کاهش می‌یابد.

از طرفی اندازه‌گیری همراه با خطای تصادفی روی مقادیر «متغیرهای مستقل» (Independent Variables)، باعث تغییر در پارامترها و ضرایب مدل رگرسیونی شده و روی بعضی از آزمون‌ها مربوط به صحت مدل رگرسیونی تاثیر گذار هستند.

عبارت خطای تصادفی، ممکن است دارای توزیع‌های آماری مختلفی باشد. برای آشنایی با تابع احتمال‌های مختلف برای عبارت خطا بهتر است نوشتار توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس را مطالعه کنید. استفاده از توزیع‌های مختلف، با توجه به شرایط داده‌ها و تعمیم قضیه حد مرکزی، توجیه پذیر است.

منابع خطای سیستماتیک

همانطور که گفته شد، خطای سیستمی معمولا ناشی از ابزار اندازه‌گیری یا تغییر در محیط اندازه‌گیری است که سنجش مقدار واقعی را دچار تغییر می‌کند. خطای مشاهداتی در آمار در بخش خطای سیستماتیک، ممکن است به علت تنظیم نادرست نقطه صفر بوده یا درصدی از مقدار واقعی را شامل شود.

خطای مشاهداتی و اثرات کالیبراسیون

یک آزمایشگر را در نظر بگیرید که قرار است تعداد نوسانات یک آونگ را اندازه‌گیری کند. اگر او به جای اندازه‌گیری در ثانیه صفر، مقادیر را برحسب ثانیه ۱، اندازه‌گیری کند، همه مقادیر یک ثانیه خطا دارند (خطای صفر) در نتیجه می‌توان مقدار خطا را ثابت و مشخص فرض کرد.

ولی اگر این آزمایشگر کار اندازه‌گیری زمان را بیست بار تکرار کند، و هر بار هم براساس زمان یا ثانیه ۱، اندازه‌گیری را انجام دهد، آنگاه مقدار میانگین نتایج بدست آمده دارای خطای درصدی (Percentage Error) است. در نتیجه پاسخ بدست آمده برای اندازه‌گیری دوره تناوب آونگ دارای مقدار خطای بسیار بزرگتری نسبت به مقدار واقعی خواهد بود. مشخص است که در اینجا خطای ناشی از کالیبراسیون نادرست رخ داده است.

یک رادار را در نظر بگیرید که قرار است فاصله اجسام را تخمین بزند. ممکن است فاصله اندازه‌گیری شده توسط رادار، دارای خطای سیستمی باشد زیرا در صورت کاهش سرعت امواج در هوا، در اثر دما یا رطوبت، تخمین فاصله اجسام توسط رادار، دچار خطای سیستمی می‌شود. تعیین نادرست نقطه صفر (کالیبره کردن فقط در یک محیط و شرایط خاص) در چنین وضعیتی باعث ایجاد خطای سیستماتیک خواهد شد.

از طرفی خطای سیستم می‌تواند ناشی از به کارگیری یک مدل ریاضیاتی یا قانون فیزیکی رخ دهد. برای مثال تناوب یک آونگ را در نظر بگیرید که تغییرات کوچک تکیه‌گاه آونگ در محاسبات در نظر گرفته نشده است. به این ترتیب اندازه‌گیری دوره تناوب این آونگ دچار خطای سیستماتیک خواهد شد.

خطای مشاهداتی در مقدار و جهت خطا

ممکن است خطای سیستماتیک ثابت بوده یا متناسب با مقدار واقعی باشد. حتی ممکن است این خطا را مرتبط با عوامل دیگر (مانند میزان دما و رطوبت) دانست. هنگامی که خطای سیستماتیک ثابت باشد، می‌توان علت وجودی آن را عدم تنظیم نقطه صفر دستگاه اندازه‌گیری در نظر گرفت.

ولی اگر مقدار خطای سیستمی متغیر باشد ممکن است علاوه بر مقدار، علامت یا جهت مقدار خطا نیز تغییر کند. برای مثال یک دماسنج را در نظر بگیرید که دارای خطای سیستماتیک ۲٪ است. این امر به این معنی است که اگر دمای واقعی سه ماده به ترتیب برابر با ۲۰۰، صفر و ۱۰۰- درجه باشند،  این دما سنج با توجه به خطای درصدی، دمای 204، صفر و 102- را نشان می‌دهد. واضح است که میزان خطای سیستماتیک در این حالت برای سه ماده به ترتیب 4+، 0 و 2- درجه است. مشخص است که این دما سنج برای حرارت‌های بالای صفر درجه، دچار خطای بیش‌برآورد و برای دماهای کمتر از صفر، کم‌برآورد می‌شود ولی برای دمای صفر درجه، خطای صفر را نشان می‌دهد. بنابراین در نقطه صفر درجه، میزان خطا به درستی مشخص نشده است.

خطای مشاهداتی در تغییرات نسبت به مبدا

خطای سیستماتیک متغیر، نسبت به خطای سیستماتیک ثابت، راحت‌تر شناسایی می‌شوند. در این حالت با تکرار عمل اندازه‌گیری، روند تغییرات به واسطه زمان به سادگی دیده می‌شود. ولی اگر تغییرات به صورت تصادفی (خطای تصادفی) رخ دهند، شناسایی آن‌ها مشکل و غیرقابل پیش‌بینی خواهد بود. به این ترتیب روند صعودی (نزولی) برای مقدار خطا، توسط رسم نمودارهای «روندنمای زمانی» (Time Series Plot) دیده می‌شود.

برای مثال حالتی را در نظر بگیرید که با تکرار اندازه‌گیری، دستگاه سنجش، گرم شده و مقدار را با خطا نشان می‌دهد. مشخص است که مقدارهای ثبت شده در این حالت سیر صعودی داشته و خطا مربوط به اندازه‌گیری متغیر و مقدار مشاهده شده رو به افزایش است.

اگر هیچ الگوی مشخصی برای اندازه‌های تکراری، مشخص نشود، بهتر است برای سنجش ابزار اندازه‌گیری و کشف خطای سیستماتیک، از سنجش یک مقدار شناخته شده (استاندارد) استفاده شود.

برای مثال، تصور کنید که زمان نوسان آونگ توسط یک زمان‌سنج دقیق چندین بار ثبت شده و مقادیر حول میانگین به صورت تصادفی در تغییر هستند. خطای سیستماتیک در صورت وجود، می‌تواند به وسیله مقایسه ثانیه‌ها و واحد زمانی زمان‌سنج با یک زمان‌سنج دقیق دیگر مشخص شود. به این ترتیب تند یا کند بودن زمان سنج، کشف شده و خطای سیستماتیک قابل اندازه‌گیری می‌شود.

به این ترتیب مشخص است که مطابقت دستگاه‌های اندازه‌گیری با استانداردها برای سنجش دقیق، امری ضروری است. به همین علت دستگاه‌های ولت‌متر و آمپرمتر باید به صورت دوره‌ای براساس استانداردها، تطبیق داده شوند.

خطاهای سیستماتیک همچنین با اندازه‌گیری مقادیری که از قبل سنجش شده‌اند، قابل تشخیص است. به عنوان مثال، دقت یک طیف سنج را می‌توان با استفاده از طول موج خطوط D از طیف الکترومغناطیسی سدیم که برابر با 600 نانومتر و 589.6 نانومتر هستند، مورد بررسی قرار داد.

شناسایی خطاهای سیستماتیک به سختی صورت می‌گیرد زیرا تا زمانی که آن‌ها را از سنجش‌ها و مقادیر اندازه‌گیری شده خارج نکنیم، قادر به محاسبه آن‌ها نخواهیم بود. اثر چنین خطاهایی با تکرار اندازه‌گیری یا با میانگین‌گیری از تعداد زیاد مشاهدات از بین نمی‌رود. همانطور که گفته شد، یک روش معمول برای از بین بردن خطای سیستماتیک ثابت، کالیبراسیون ابزار اندازه‌گیری است.

فیلم آموزش کالیبراسیون تجهیزات اندازه‌گیری

اشاره کردیم که بخشی از خطای مشاهداتی در آمار می‌تواند ناشی از «خطای سیستماتیک» (Systematic Error) باشد. خوشبختانه در یکی از آموزش‌های فرادرس با عنوان «آموزش کالیبراسیون تجهیزات اندازه گیری» به این موضوع پرداخته شده است. این دوره آموزشی، موضوعات مرتبط با انداه‌گیری و کالیبراسیون تجهیزات اندازه‌ گیری را ارائه کرده است. در نتیجه با بهره‌گیری از این آموزش، علاقه‌مندان می‌‌توانند کاربرد کالیبراسیون را در استانداردهای مختلف صنعتی فرا گرفته و نحوه اجرای آن را بیاموزند. از طرفی مباحث مربوط به انواع منابع خطا و موضوع عدم قطعیت اندازه‌ گیری نیز در این آموزش مورد بحث قرار می‌گیرد.

فیلم آموزش کالیبراسیون تجهیزات اندازه گیری در فرادرس

کلیک کنید

درس یکم از این آموزش اختصاص به مفاهیم اولیه و اساسی اندازه‌گیری و کالیبراسیون دارد. همچنین خطای اندازه‌گیری و ویژگی عدم قطعیت مورد بررسی قرار می‌گیرد. در درس دوم نیز موضوعات مربوط به درستی و دقت در اندازه‌گیری به همراه سلسله مراتب و هرم کالیبراسیون آموزش داده می‌شود. درس سوم هم به سیستم‌های مدیریت کیفیت و جایگاه کالیبراسیون در آن‌ها پرداخته و فواصل زمانی و شرایط محیطی کالیبراسیون برای کاهش خطای مشاهدات نیز بررسی می‌شود.

خلاصه و جمع‌بندی

در این نوشتار با دو نوع خطای مهم در روش‌های اندازه‌گیری آشنا شدید. مشخص شد که بررسی خطای مشاهداتی در آمار چگونه می‌تواند نتایج حاصل از آزمایشات علمی را دقیق‌تر کرده و بخش خطای تصادفی را از خطای سیستمی جدا کند. همچنین کاربردهایی از خطای مشاهداتی در آمار، بخصوص در فنون رگرسیونی نیز مورد بحث قرار گرفت.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار و احتمالات
• آموزش محاسبات علمی و آماری با R – مقدماتی
• گزارش کار آزمایشگاه — اصول نگارش
• اعداد توان دار — به زبان ساده

^^