حساب پیمانه ای – به زبان ساده
حساب پیمانه ای نوع ویژهای از حساب است که اعداد صحیح را شامل میشود. هدف این نوشته ارائه مبانی حساب پیمانهای و همچنین معرفی برخی مسائل نسبتاً پیشرفته و جالبتر است که به کمک حساب پیمانهای به سادگی حل میشوند.


کار خود را با معرفی یک ساعت آغاز میکنیم که به جای عدد 12 آن عدد 0 استفاده شده است.

اگر از نیمه روز آغاز کنیم، عقربههای ساعت به ترتیب به صورت زیر هستند:

این همان روشی است که برای شمارش پیمانه 12 استفاده میکنیم. بدین ترتیب زمانی که لازم باشد 1 را به 11 اضافه کنیم به 0 میرسیم همین مطلب در مورد هر پیمانه دیگری نیز صدق میکند. در پیمانه 5 به صورت زیر میشماریم:

همچنین میتوانیم در پیمانه 5 به سمت عقب بشماریم. هر بار که 1 را از 0 کسر میکنیم به 4 می رسیم. بنابراین عددهای صحیح از 12 تا 0 در پیمانه 5 به صورت زیر نوشته میشوند:
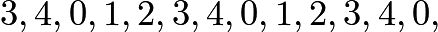
که 12 همان 3 در پیمانه 5 است. از آنجا که همه اعداد صحیح را میتوان به صورت 0، 1، 2، 3 یا 4 نشان داد ما به این اعداد صحیح نامهای خاصی میدهیم که کلاسهای باقیمانده پیمانه 5 هستند. به طور کلی برای هر عدد طبیعی n که بزرگتر از 1 است، باقیماندههای پیمانه n عددهای صحیحی به صورت اعداد کامل کمتر از 1-n هستند:

این وضعیت به ارتباط بین هر عدد صحیح و باقیماندههایش بر اساس قضیه تقسیم مربوط است. با این که شاید این موضوع در ابتدا چندان مفید به نظر نرسد؛ اما شمارش به این ترتیب میتواند به حل انواع مختلفی از مسائل نظریه اعداد به روشی بسیار آسانتر کمک کند.
باقیمانده
a را باقیمانده عدد n به پیمانه m میگوییم، وقتی شرایط زیر برقرار باشد:
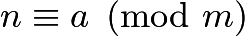

همنهشتی (هم ارزی)
برای این که بگوییم همه اعداد صحیح به طور یکسانی یکی از باقیماندههای پیمانه 5 هستند، یک روش ریاضیاتی وجود دارد. برای نمونه میگوییم 7 و 2 به پیمانه 5 همنهشت هستند. این وضعیت با نماد ≡ نمایش مییابد. به بیان دیگر این به آن معنی است که در مبنای 5 این دو عدد صحیح، باقیمانده یکسانی به پیمانه 5 دارند:

بخش (mod 5) اعلام میکند که مشغول کار با اعداد صحیح به پیمانه 5 هستیم. در پیمانه 5 دو عدد صحیح زمانی همنهشت هستند که اختلاف آنها مضربی از 5 باشد. به طور کلی دو عدد صحیح a و b به پیمانه n همنهشت خوانده میشوند در صورتی که a-b مضربی از n باشد. به بیان دیگر در صورتی که یک عدد صحیح باشد. در غیر این صورت که به این معنی است که a و b به پیمانه n با یکدیگر همنهشت نیستند.
مثال
زیرا 30= 1 -31 مضربی از 10 است.
زیرا یک عدد صحیح است.
زیرا مضربی از 3 نیست.
زیرا یک عدد صحیح نیست.
مسئله نمونه
باقیمانده 311 به پیمانه 4 را بیابید:
راهحل
از آنجا که 311 تقسیم بر 77 باقیماندهای برابر با 3 دارد، میدانیم که
و میگوییم 3 باقیمانده 311 به پیمانه 4 است.
راهحل دیگر
از آنجا که 11+300 = 311 میدانیم که
اینک میتوانیم آن را به روشی سادهتر حل کنیم:
و 3 باقیمانده 311 به پیمانه 4 است.
سادهتر کردن محاسبات
در همه موارد برای حل مسائل مختلف نیازمند محاسبات پیچیده نیستیم. اگر بخواهیم باقیمانده تقسیم اعداد بر عدد صحیح n را بدانیم، در این صورت میتوانیم به طور مستقیم با آن باقیماندهها به پیمانه n کار کنیم. در ادامه برای تفهیم بهتر موضوع چند مثال ارائه کردهایم:
جمع
فرض کنید میخواهیم یکان عدد حاصل جمع زیر را بدانیم:
4339 + 688 + 791 + 2403
میتوان مجموع فوق را که برابر با 8221 است محاسبه کرد و متوجه شد که رقم یکان برابر با 1 است. با این وجود میتوانیم رقم یکان حاصل جمع را با محاسبات بسیار کمتری نیز پیدا کرد. بدین منظور کافی است ارقام یکان اعداد فوق را با هم جمع کرد:
21 = 9 + 8 + 1 + 3
رقم یکان مجموع فوق برابر با 1 است که باید برابر با همان رقم یکان مجموع اعداد چهار رقمی باشد که قبلاً محاسبه کردیم.
در برخی موارد کافی است از باقیماندهها استفاده کنیم
هر یک از اعداد صحیح را میتوان به صورت مضربی از 10 و باقیمانده نوشت:
3 + 10 × 240 = 2403
1 + 10 × 79 = 791
8 + 10 × 68 = 688
9 + 10 × 433 = 4339
زمانی که چهار عدد صحیح فوق را با هم جمع کنیم، نتیجه زیر حاصل میشود:
(9 + 10 × 433) + (8 + 10 × 68) + (1 + 10 × 79) + (3 + 10 × 240)
(9 + 8 + 1 + 3) + 10 × (433 + 68 + 79 + 240) =
در این مرحله میتوانیم ببینیم که ارقام یکان به صورت مجزا دستهبندی شدهاند و به مضرب 10 که تأثیری بر رقم یکان مجموع ندارد اضافه میشوند:
8221 = 21 + 8200 = 21 + 10 × 820 =
راهحل با استفاده از حساب پیمانهای
اکنون دوباره از ابتدا راهحل خود را با استفاده از حساب پیمانهای بررسی میکنیم. دقت کنید که:
از آنجا که تنها کافی است باقیماندههای 10 مجموع را اضافه کنیم، باقیماندههای مجموعها را جمع میکنیم:
بنابراین رقم یکان مجموع تنها میتواند 1 باشد.
قاعده جمع
به طور کلی وقتی a، b، c و d اعداد صحیح باشند و m عدد صحیح مثبتی باشد که:
قاعده زیر همواره برقرار است:
و این همان کاری است که در مثال فوق انجام دادیم. در واقع میتوان جفت عددهای صحیحی به هر دو طرف معادله فوق اضافه کرد و این اصل ساده را تکرار کرد.
اثبات قاعده جمع
فرض کنید و باشد که l و k اعداد صحیح هستند. با افزودن دو معادله به همدیگر نتیجه زیر حاصل میشود:
که معادل این است که بگوییم:
تفریق
حالت فوق که در مورد جمع اشاره کردیم در مورد تفریق نیز صدق میکند:
مثال
باقیمانده تقسیم تفاضل 60002 و 601 بر 6 را بیابید:
راهحل
دقت کنید که و . بنابراین:
از این رو
و بنابراین 1 باقیمانده تفاضل فوق بر 6 است. میتوانید با انجام تقسیم فوق درستی این گزاره را بررسی کید.
قاعده تفریق
وقتی a، b، c و d اعداد صحیح و m عدد صحیح مثبتی باشد که روابط زیر برقرار باشد:
قاعده زیر برقرار است:
ضرب
حساب پیمانهای هنگام ضرب کردن مزیتهای بسیار بیشتری نسبت به عملیات جمع و تفریق از خود نشان میدهد. در مثال زیر این وضعیت را بررسی میکنیم.
مثال
علی 44 کارتن نوشابه در کامیون خود دارد. قوطیهای نوشابه در هر کارتن برابر با عدد فرد 113 هستند. وی قصد دارد این نوشابهها را در صندوقهای 12 تایی به فروش برساند. پس از این که همه نوشابهها در صندوقها جای گرفتند، در نهایت در صندوق آخر چند قوطی نوشابه قرار میگیرد؟
راهحل
ابتدا باید اشاره کنیم که در این مسئله باید باقیمانده تقسیم حاصلضرب 43 × 113 بر 12 را بیابیم. اکنون میتوانیم هر یک از 44 و 113 را بر مبنای مضرب 12 و باقیماندهها بنویسیم:
8 + 12 × 3 = 44
5 + 12 × 9 = 113
بدین ترتیب روش خوبی برای مشاهده حاصلضرب آنها پیدا میکنیم:
(5 + 12 × 9) (8 + 12 × 3) = 113 × 44
با استفاده از ضرب داخلی به نتیجه زیر میرسیم:
(5 × 8) + (9 × 8 + 5 × 3) + 2^12 × (9 × 3)
اینک میتوانیم ببینیم که هر بخش از حاصلضرب نتیجه ضرب کردن 12 است به جز حاصلضرب باقیماندهها در مواردی که 44 و 13 بر 12 تقسیم میشوند. این بخش از حاصلضرب به صورت 40 = 5 × 8 است که باقیماندهای برابر با 4 هنگام تقسیم بر 12 بر جای میگذارد. بنابراین علی پس از پر کردن همه صندوقهای 12 تایی، 4 قوطی نوشابه خواهد داشت.
راهحل با استفاده از حساب پیمانهای
ابتدا باید توجه کنیم که:
از این رو
یعنی 4 نوشابه باقی میماند. مشاهده میکنید که این روش محاسبه بسیار سادهتر است.
قاعده ضرب
وقتی a، b، c و d اعداد صحیحی باشند و m یک عدد صحیح مثبت باشد که:
قاعده زیر برقرار است:
توان
از آنجا که توان صرفاً تکرار عملیات ضرب است، میتوان تصور کرد که حساب پیمانهای میتواند به حل آسانتر بسیاری از مسائل شامل توان نیز کمک کند. در واقع مزیت چنین محاسباتی بسیار بیشتر است. باید اشاره کرد که حساب پیمانهای در مورد مسائلی مانند زیر بسیار مفید است.
مسئله اول
آخرین رقم در صورتی که 1000 تا 7 به توان رسیده باشند و تنها یک 7 در میانه باشند چه خواهد بود؟
این مسئله با استفاده از پیمانهها قابل حل است. مسئله فوق را میتوان به صورت نیز نوشت. سپس میبینیم که 7 به پیمانه 4 با 1- همنهشت است از این رو میتوانیم از این واقعیت استفاده کرده و 7 ها را با 1- جایگزین کنیم، چون 7 الگوی تکراری دوره 4 برای رقمهای یکان دارد. برابر با 1 است و از این رو است که آخرین رقم محسوب میشود.
مسئله دوم
ارقام یکان و دهگان کدام هستند؟
به طور نظری میتوان مسئله را با محاسبه حل کرد؛ اما این کار فرایندی بسیار زمانبر است. به علاوه اطلاعاتی به دست میدهد که مورد نیاز ما نیستند. از آنجا که تنها به ارقام یکان و دهگان عدد مورد بحث نیاز داریم، کافی است باقیمانده تقسیم عدد بر 100 را بیابیم. به بیان دیگر همه اطلاعات مورد نیاز را میتوان با استفاده از حساب به پیمانه 100 به دست آورد.
ابتدا چند توان نخست 7 به پیمانه 100 را مینویسیم:
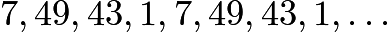
مشاهده میکنید که الگویی وجود دارد. میبینیم که . بنابراین برای هر عدد صحیح مثبت k داریم:
به طور خاص میتوانیم بنویسیم:
با در نظر گرفتن خصوصیت ضرب فوق نتیجه میشود که:
از این رو بر اساس تعریف همنهشتی تفاضل $$ $${7^{1942}} با 49 مضربی از 100 است. از آنجا که هر دو عدد صحیح و مثبت هستند، این بدان معنی است که ارقام یکان و دهگان یکسانی دارند. این ارقام به ترتیب برابر با 4 و 9 هستند.
مسئله سوم
آیا میتوان عددی یافت که هم مضرب 2 باشد و هم مضربی از 4 نباشد و هم این که یک مربع کامل باشد؟
پاسخ سؤال فوق منفی است، زیرا اگر سؤال را بازنویسی کنیم میبینیم که از ما میخواهد عدد صحیح n را طوری بیابیم که در معادله صدق کند.
با گرفتن پیمانه 4 از هر دو طرف میفهمیم که . اکنون میدانیم که چه x و چه هرگز مضربی از 4 به علاوه 2 نیستند و از این رو با حالتهای زیر کار میکنیم:
بدین ترتیب مطمئن میشویم که چنین عددی ناممکن است.
سخن پایانی
اعداد صحیح a، b، c و d و یک عدد صحیح مثبت m را طوری در نظر بگیرید که و باشد. در حساب پیمانهای روابط زیر برقرار هستند:
- جمع:
- تفریق:
- ضرب:
- تقسیم: که e یک عدد صحیح مثبت است که بر a و b بخشپذیر است.
- توان: که e یک عدد صحیح مثبت است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش ریاضی پایه دانشگاهی
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- آموزش محاسبات سریع ریاضی
- آموزش ریاضیات عمومی ۱
- آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
==













این سایت از همه سایت ها بهتر همنهشتی رو برای من شفاف سازی کرد مخصوصا مثال ساعتتون واقعا عالی بود سپاس از شما??