تنش در مخازن — به زبان ساده

پیش‌تر در وبلاگ فرادرس مفاهیم مربوط به تنش و کرنش را توضیح دادیم. در این مطلب قصد داریم تا نوع خاصی از تنش‌ را مورد بررسی قرار دهیم.  این نوع از تنش در مخازن جدارنازک ایجاد شده و در طراحی خط لوله‌ها و مخازن از آن استفاده فراوانی می‌شود.

البته پیشنهاد می‌کنیم قبل از مطالعه، مطالب مولفه های تنش و کرنش در حالت برش خالص و تنش نرمال و کرنش نرمال نیز مطالعه شوند.

مقدمه

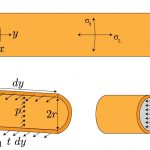
در حالت کلی اگر یک مخزن حاوی گاز بوده و فشار گاز با فشار محیط متفاوت باشد، در مخزن دو نوع تنش طولی و مماسی ایجاد خواهد شد.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

در این مطلب نحوه محاسبه تنش را در مخازن کروی و استوانه‌ای توضیح خواهیم داد. در شکل زیر این نوع از مخازن نشان داده شده است.

محاسبه تنش در مخازن

به منظور محاسبه تنش در هر سیستمی، در ابتدا باید مقاطع به درستی شناسایی شده و برش زده شوند. برای برآورد تنش در مخازن جدارنازک نیز همین قاعده صادق است.

تنش در مخازن استوانه‌ای

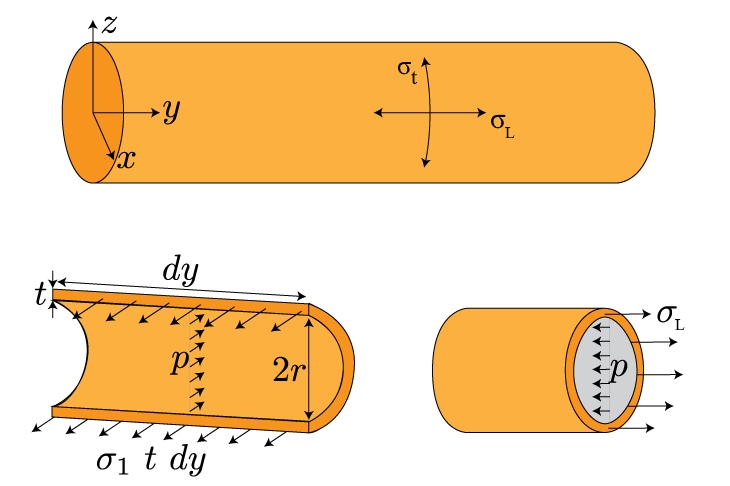
مطابق با شکل زیر مخزنی استوانه‌ای را در نظر بگیرید. فرض کنید این مخزن حاوی گازی با فشار p است. مطابق با شکل زیر قطر و ضخامت این مخزن به ترتیب برابر با D و t و طول آن برابر با L در نظر گرفته شده‌اند. برای بدست آوردن تنش مماسی، مخزن مطابق با شکل زیر برش زده می‌شود.

پوسته آبی رنگ در تعادل است؛ بنابراین نیروی ناشی از فشارِ p با نیروی ناشی از تنش مماسی برابر است. در نتیجه با نوشتن رابطه تعادل داریم:

$$\Large 2 T = F$$

از طرفی نیروی T برابر با حاصل ضرب تنشِ $$\large \sigma _ t$$ در مساحتِ tL است. بنابراین رابطه فوق را می‌توان به صورت زیر بازنویسی کرد.

$$\Large 2 ( \sigma _ t t L ) = p D L$$

$$\Large 2 t \sigma _ t = p D$$

نهایتا تنش مماسی در یک مخزن جدار نازکِ استوانه‌ای با فشار p برابر با مقدار زیر بدست می‌آید.

$$\Large \boxed {\sigma_t = \dfrac { p D } { 2 t } }$$
رابطه ۱

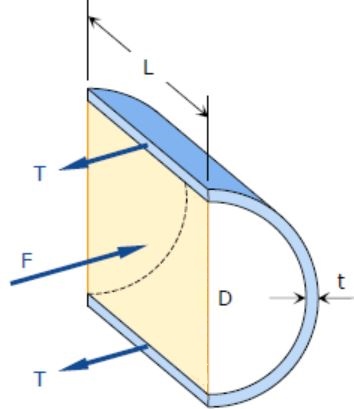
برای بدست آوردن تنش طولی کافی است تا مخزن استوانه‌ای مطابق با شکل زیر، به صورت عمود به طول استوانه برش زده شود.

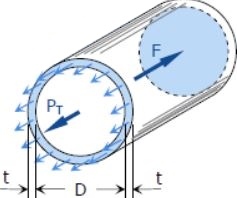
مطابق با شکل فوق، نیروی وارد به انتهای استوانه برابر است با:

$$\Large F = p A = p \dfrac { \pi} {4} D ^2$$

از طرفی تنش طولی تنها روی بخش جدار نازک اعمال می‌شود. مساحت این قسمت برابر با $$\large A = \pi D t$$ است. از این رو نیروی ناشی از تنش طولی نیز برابر است با:

$$\Large P _ T = \sigma _ L \pi D t$$

در مرحله بعد معادله تعادل نیرویی را به صورت زیر بیان می‌کنیم.

$$\Large \Sigma F _ H = 0$$
$$\Large P_T = F$$
$$\Large \sigma _ L \, \pi D t = p \dfrac {\pi} { 4 } D ^ 2$$

نهایتا تنش طولی به صورت زیر بدست می‌آید.

$$\Large \boxed { \sigma _ L = \dfrac { p D } { 4 t } }$$
رابطه ۲

توجه داشته باشید در روابط فوق منظور از فشار، در حقیقت اختلاف فشار داخل و بیرونِ مخزن است. بنابراین با فرض این که فشار داخلی برابر با p_i و فشار خارجی برابر با p_o باشد، رابطه زیر را می‌توان برای تنش طولی بیان کرد.

$$\Large \sigma _ L = \dfrac { ( p _ i - p _ o ) D } { 4 t }$$

با توجه به روابط ۱ و ۲، رابطه زیر را می‌توان بین تنش‌های افقی و عمودی نوشت.

$$\Large \sigma _ t = 2 \sigma _ L$$

تنش در مخازن کروی

به دلیل متقارن بودن شکل کره نسبت به تمامی محور‌هایی که از مرکز آن عبور می‌کنند، تنش در پوسته یک مخزن کروی، در تمامی جهات با هم برابر هستند.

فیلم آموزش مهندسی مخازن نفت و گاز 1 در فرادرس

کلیک کنید

از این رو به منظور محاسبه تنش، تنها کافی است تا مطابق با شکل زیر، کره را در جهتی دلخواه برش بزنید.

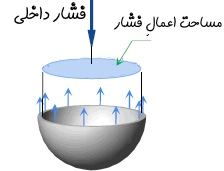
نیروی داخلیِ ناشی از فشار که به نیمکره وارد می‌شود، برابر است با:

$$\Large P = p ( \frac { 1 } { 4 } \pi D ^ 2 )$$

این نیرو برابر با تنشی است که به جداره وارد می‌شود. بنابراین می‌توان گفت:

$$\Large P_T = F$$
$$\Large F = P$$
$$\Large \sigma A = p (\frac {1}{4} \pi D ^ 2)$$
$$\Large \sigma \pi D t = p (\frac {1}{4} \pi D ^ 2)$$

نهایتا تنش در جداره یک مخزن کروی با فشار p برابر است با:

$$\Large \boxed { \sigma = \dfrac { p D } { 4 t } }$$

در ادامه مثال‌هایی مطرح شده که پیشنهاد می‌کنیم به منظور درک بهترِ موضوع، آن‌ها را مطالعه فرمایید.

مثال ۱

مخزنی استوانه‌ای را در نظر بگیرید که ضخامت جداره آن برابر با ۲۰mm است. هم‌چنین قطر این مخزن را برابر با ۴۵۰mm در نظر گرفته شده و طول آن نیز برابر با 2m است. فرض کنید بیشترین تنشی که این مخزن می‌تواند در راستای طولی تحمل کند، برابر با ۱۴۰MPa و بیشترین تنش مماسیِ قابل تحمل برابر با 60MPa باشد. در این صورت بیشترین فشاری که گاز درون استوانه می‌تواند داشته باشد، چقدر است؟

در ابتدا از فرمول مربوط به تنش مماسی در مخازن استوانه‌ای استفاده کرده و مقدار فشار قابل قبول را بدست می‌آوریم. با انجام این کار داریم:

$$\Large \sigma _ t = \dfrac { p D } { 2 t }$$

$$\Large 60 = \dfrac{ p (450)}{ 2 (20)}$$

$$\Large p = 5.33 \, \text{MPa}$$

از طرفی فشار متناسب با تنش طولی نیز به صورت زیر قابل محاسبه است.

$$\Large \sigma _ l = \dfrac { p D } { 4 t }$$

$$\Large 140 = \dfrac { p (450 ) } { 4 ( 2 0)}$$

$$\Large p = 24.89 \, \text{MPa}$$

بنابراین در این حالت تنش بیشتری بدست آمد. نهایتا با مقایسه دو فشار 5.33MPa و 24.89MPa فشار کمتر را به عنوان پاسخ نهایی در نظر می‌گیریم. بنابراین بیشترین فشار قابل قبول برای این مخزن برابر است با:

$$\Large p = 5.33 \, \text{MPa}$$

مثال 2

قطر مخزنی کروی و جدار نازک ۴ft است. با فرض این که ضخامت این مخزن برابر با $$\large \frac { 5 } { 1 6 } inch$$ باشد، بیشترین فشار قابل قبول موجود در آن را بدست آورید. فرض کنید این مخزن می‌تواند تنشی معادل با 8000psi را تحمل کند.

به سادگی و با استفاده از رابطه ۲، می‌توان بیشترین فشارِ معادل با بیشترین تنش قابل قبول را به صورت زیر محاسبه کرد.

$$\Large \sigma = \dfrac { p D } { 4 t }$$

$$\Large 8000 = \dfrac { p ( 4 \times 1 2 ) } { 4 ( \frac{5} { 16} ) }$$

$$\Large p = 208.33 \, \text{psi}$$

در این مطلب نحوه محاسبه تنش در مخازن جدار نازک توضیح داده شد. با این حال در مورد نحوه محاسبه تنش‌های برشی و هم‌چنین در مورد مفاهیم تنش صحبت خواهیم کرد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی عمران و مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• تحلیل پیچش در لوله های جدار نازک – آموزش جامع
• تعیین مولفه های تنش و کرنش در حالت برش خالص – آموزش جامع

^^