تقسیم ذهنی و سریع — از صفر تا صد

ضرب و تقسیم از عملیاتی هستند که در زندگی روزمره بسیار به کار می‌بریم. هر چند ممکن است انجام چنین عملیاتی به صورت ذهنی مشکل و پیچیده به نظر برسد ولی می‌خواهیم به کمک چند ترفند ساده و البته کاربردی، نحوه محاسبه تقسیم ذهنی و سریع را مرور کنیم. در دیگر نوشتارهای فرادرس با جمع و تفریق ذهنی و همچنین نحوه انجام محاسبه ضرب ذهنی و سریع آشنا شدیم. در اینجا با استفاده از همه معلوماتی که براساس آن مطالب جمع‌آوری کرده‌ایم، تقسیم را با سرعت و البته دقت زیاد در ذهنمان انجام خواهیم داد.

هر چند تقسیم را برای هر دو عدد حقیقی به کار می‌برند ولی هدف ما در این نوشتار محاسبه و انجام عمل تقسیم روی مجموعه اعداد صحیح است. به همین دلیل بهتر است به عنوان مقدمه مطلب اعداد صحیح — به زبان ساده و ضرب ذهنی و سریع --- از صفر تا صد را بخوانید. همچنین خواندن جمع و تفریق ذهنی — از صفر تا صد و قواعد بخش پذیری یا عاد کردن — به زبان ساده نیز خالی از لطف نیست.

تقسیم ذهنی و سریع

عمل تقسیم جزو عملیات پایه در ریاضیات محسوب می‌شود. به همین دلیل در اکثر اوقات احتیاج داریم که چنین محاسباتی را بدون ماشین حساب یا تلفن همراه و به صورت ذهنی انجام دهیم.

انجام عمل تقسیم برای حالت کلی باید توسط روال مشخصی که در دبستان یا دبیرستان خوانده‌اید صورت گیرد ولی برای سرعت بخشیدن به انجام این عمل یا اجرای تقسیم ذهنی بهتر است خواندن متن را ادامه دهید.

ترفندهای تقسیم ذهنی

همانطور که در دیگر نوشتار فرادرس با عنوان ضرب ذهنی و سریع --- از صفر تا صد خوانده‌اید، برای انجام عمل ضرب، به خاطر سپردن جدول ضرب بسیار اهمیت دارد و همه روش‌های ضرب بر مبنای آن کار می‌کنند. دراین قسمت با مرور روش‌هایی سعی می‌کنیم، عمل تقسیم را که پیچیده‌تر از عمل ضرب به نظر می‌رسد، در ذهن انجام دهیم.

به یاد دارید که در عمل ضرب دو عدد شرکت کرده که به آن‌ها مضرب گرفته می‌شود. همچنین نتیجه عملیات ضرب نیز به نام حاصل‌ضرب معروف است. در تقسیم ولی پارامترها بیشتر هستند. فرض کنید می‌خواهید عدد $$a$$ را بر $$b$$ تقسیم کنیم. در این صورت $$a$$ را مقسوم و $$b$$ را مقسوم علیه می‌نامند. نتیجه تقسیم نیز خارج قسمت نامیده شده که آن را با $$q$$ نشان می‌دهیم. باقی‌مانده عمل تقسیم نیز با $$r$$ مشخص می‌شود. بین این چهار عدد رابطه زیر برقرار است.

$$\large a = b \times q + r$$

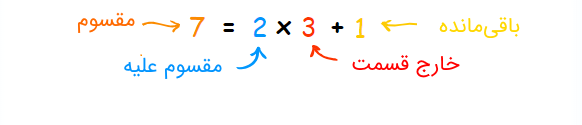
با در نظر گرفتن مقادیر صحیح برای $$b$$ ، $$a$$ و $$q$$ همچنین مثبت $$r$$، می‌توانیم تقسیم را به دسته‌بندی مقسوم توسط مقسوم علیه تشبیه کنیم. به این ترتیب مشخص می‌شود که در $$a$$، تعداد $$q$$ دسته $$b$$تایی و تعداد $$r$$ واحد یا دسته تکی وجود دارد.

در صورتی که باقی‌مانده یا $$r$$ برابر با صفر باشد، $$a$$ را بر $$b$$ بخش‌پذیر می‌نامند.

می‌توانیم عمل تقسیم را به صورت کسر نیز برای اعداد صحیح نشان دهیم. در نتیجه تقسیم $$a$$ بر $$b$$ به صورت $$\frac{a}{b}$$ نیز نوشته و محاسبه می‌شود.

$$\large  \dfrac{a}{b} = q \dfrac{r}{b}$$

نمایش تقسیم به صورت کسر نیز می‌تواند در حل بسیاری از تقسیم‌های ذهنی، ما را یاری رساند.

در این قسمت با بعضی از ترفندهای ساده آشنا خواهیم شد. برای مثال تقسیم یک عدد بر ۱۰ یا ۱۰۰ و همچنین تقسیم بر ۵ و ۵۰ را مشخص خواهیم کرد. در انتها نیز به کمک اتحادهای جبری و همچنین الگوریتم تقسیم، محاسبات تقسیم ذهنی و سریع را مرور خواهیم کرد.

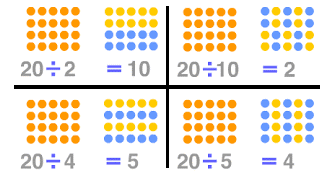
تقسیم بر ۱۰ و توان‌هایی از آن

فرض کنید می‌خواهیم تقسیم عدد ۸۵۰ را بر ۱۰ محاسبه کنیم. همانطور که گفتیم، این تقسیم به این معنی است که در ۸۵۰ چند دسته ۱۰ تایی وجود دارد. خوب این موضوع با در نظر گرفتن دهگان و صدگان عدد ۸۵۰ بسیار ساده مشخص می‌شود. ۸۵۰، صدگانی برابر با ۸ و دهگانی برابر با ۵ دارد که نشان می‌دهد ۸۰ دسته ۱۰ تایی و ۵ دسته ده‌تایی دیگر در این عدد حضور دارند.

به سادگی دیده می‌شود که نتیجه تقسیم ۸۵۰ بر ۱۰، در این صورت برابر با ۸۵ خواهد بود. بنابراین با توجه به این موضوع تقسیم اعدادی که دارای یکانی برابر با صفر هستند، بر ۱۰ برابر است با همان عدد در زمانی که یکان را حذف کنیم. این تکنیک به «حذف صفر»، معروف است.

خارج قسمت تقسیم اعداد با یکان برابر با صفر، بر عدد ۱۰، برابر است با همان عدد بدون در نظر گرفتن یکان آن.

حال فرض کنید که عمل تقسیم بر ۱۰ یا توان‌هایی از آن را به صورت کسری نمایش دهیم. در این صورت برای تقسیم ۸۵۰ بر ۱۰ خواهیم داشت:

$$\large \dfrac{850}{10} = \dfrac{85 \times 10 } { 10} = 85 \dfrac{\not{10}}{\not{10}} = 85$$

نکته: همین عمل را برای تقسیم بر توان‌های دیگر ۱۰ نیز می‌توان انجام داد. برای مثال تقسیم ۱۵۰۰ بر ۱۰۰ نیز به شکل زیر خواهد بود.

$$\large \dfrac{1500}{100} = \dfrac{15 \times 100 } { 100} = 15 \dfrac{\not{100}}{\not{100}} = 15$$

این بار تقسیم بر ۱۰ را به شکلی فرض می‌کنیم که عدد مقسوم به صورت اعشاری باشد. به مثال‌های زیر توجه کنید.

مثال ۱

حاصل تقسیم اعشاری ۱۵۵۰٫۷۵ بر ۱۰ به شکل زیر نوشته می‌شود، زیرا در این عدد ۱۵۵ دسته ۱۰ تایی وجود دارد و باقی مانده تقسیم صحیح نیز برابر است با ۰٫۰۷۵ واحد ۱۰ تایی است.

$$\large 1550.75 \div 10 = 155.075$$

همینطور تقسیم ۱۵۵۰٫۰۷۵ بر ۱۰۰ نیز به این ترتیب خواهد بود. زیرا ۱۵ دسته ۱۰۰ تایی در این عدد وجود داشته و باقی‌مانده آن نیز ۰٫۵۰۷۵ واحد ۱۰۰ تایی است.

$$\large 1550.75 \div 100 = 15.5075$$

همینطور تقسیم ۱۵۵۰٫۰۷۵ بر ۱۰۰۰ نیز به این ترتیب خواهد بود. زیرا یک دسته ۱۰۰۰ تایی در این عدد وجود داشته و باقی‌مانده آن نیز ۰٫۵۵۰۷۵ واحد هزارتایی است.

$$\large 1550.75 \div 1000 = 1.55075$$

به این ترتیب می‌توانیم قانون زیر را برای تقسیم عدد بر ۱۰ و توان‌های صحیح مثبت آن در نظر گرفت.

با هر بار تقسیم عددی بر ۱۰، علامت اعشاری یک واحد به سمت چپ حرکت می‌کند.

تقسیم یک عدد بر ۵ و توان‌های مختلف آن

برای تقسیم یک عدد بر ۵ بهتر است تقسیم را به صورت تقسیم عدد بر ۱۰ یا توان‌های آن بنویسیم. برای این منظور مراحل زیر را انجام می‌دهیم.

• مقسوم را در ۲ ضرب کنید. برای این کار از تکنیک‌های ضرب استفاده کنید.
• عدد حاصل را بر ۱۰ یا توان‌های مناسب آن تقسیم کنیم. به یاد دارید که تقسیم یک عدد بر توان‌هایی از ۱۰ به صورت حرکت علامت ممیز اعشار  به سمت چپ است.

توجه دارید که با این کار عمل تقسیم را به صورت یک کسر بیان کرده‌ایم. از آنجایی ضرب صورت و مخرج یک کسر در عدد ثابت (غیر از صفر) تغییری در کسر ایجاد نمی‌کند، عمل تقسیم نیز تغییر نخواهد کرد و فقط عملیات راحت‌تر صورت خواهند گرفت.

$$\large \dfrac{a}{b} = \dfrac{ a \times c } { b \times c } , \;\;\; c \neq 0$$

به این ترتیب عدد $$c$$ در اینجا همان ۲ در نظر گرفته شده است.

مثال ۲

تقسیم ۶۲۵ بر ۵ را در نظر بگیرید. مراحل گفته شده را انجام می‌دهیم.

$$\large 625 \div 5$$

• عدد ۶۲۵ را در ۲ ضرب می‌کنیم. با توجه به رابطه ضرب، مقدار برابر است با ۱۲۵۰ زیرا به کمک تجزیه داریم:

$$\large 625 \times 2 = 2 \times (600 + 25) = ( 2 \times 600 ) + ( 2 \times 25 )$$

$$\large = 1200 + 50 = 1250$$

• حال علامت اعشار را یک واحد به سمت چپ حرکت می‌دهیم.

$$\large 1250 .00\;  \xrightarrow{ \text{ Left Shift }} \; 125.0$$

نکته: هر عدد صحیح، در سمت راست خود بی‌نهایت رقم اعشار برابر با صفر دارد.

مثال ۳

حاصل تقسیم ۱۰۷۵ بر ۵۰ را به کمک تکنیک یاد شده انجام می‌دهیم.

• عدد مقسوم یعنی ۱۰۷۵ را در ۲ ضرب می‌کنیم. البته این بار هم باز به کمک تجزیه و عمل ضرب می‌توانیم عملیات را انجام دهیم.

$$\large 1075 \times 2 = 2 \times ( 1000 + 75 ) = 2000 + 150 = 2150$$

• حال عدد را بر ۱۰۰ تقسیم می‌کنیم. یعنی علامت ممیز را دو رقم به سمت چپ می‌بریم، زیرا عدد را بر ۱۰۰ تقسیم کرده‌ایم.

به این ترتیب نتیجه تقسیم برابر با ۲۱٫۵۰ خواهد بود.

تقسیم و استفاده از هر دو روش

در این قسمت با استفاده از تفکیک کردن عمل تقسیم به حالت‌هایی که عمل تقسیم راحت‌تر است، محاسبات را پی می‌گیریم. به مثال‌هایی در این زمینه توجه کنید.

مثال ۴

تقسیم زیر را در نظر بگیرید. مشخص است که می‌توان مقسوم علیه یعنی ۲۰ را به صورت حاصل‌ضرب ۲ در ۱۰ در نظر گرفت.

$$\large 1840 \div 20 = \dfrac{1840}{10 \times 2 }$$

این عمل تقسیم را می‌توانیم گام به گام انجام دهیم. یعنی ابتدا ۱۸۴۰ را بر ۱۰  و نتیجه را بر ۲ تقسیم کنیم. به این ترتیب خواهیم داشت:

$$\large 1840 \div 10 = 184$$

و سپس

$$\large 184 \div 2 = 92$$

در قسمت آخر محاسبات از این حقیقت استفاده کرده‌ایم که ابتدا ۴ را بر ۲ تقسیم کرده و سپس ۱۸ را به ۲ تقسیم می‌کنیم. نتایج تقسیم را در کنار یکدیگر قرار داده تا خارج قسمت یعنی ۹۲ بدست آید.

$$\large 18 \div 2 = 9 , \;\;\; 4 \div 2 = 2$$

مثال ۵

نتیجه تقسیم ۲۹۶۰ را بر ۸۰ با روش ترکیبی انجام می‌دهیم. تقسیم را به صورت زیر می‌نویسیم.

$$\large \dfrac{2960}{80} = \dfrac{2960}{10 \times 4 \times 2 }$$

بنابراین ابتدا نتیجه تقسیم بر ۱۰ را بدست آورده، سپس تقسیم را با دیگر بخش‌های مقسوم علیه، ادامه می‌دهیم.

$$\large 2960 \div 10 = 296$$

سپس

$$\large \dfrac{296}{4 \times 2 }$$

برای محاسبه تقسیم ۲۹۶ بر ۴ از یک ترفند کمک می‌گیریم. نزدیکترین عدد به ۲۹۶ که بر ۴ بخش‌پذیر است، عدد ۳۰۰ است. خارج قسمت ۳۰۰ بر ۴ برابر است با ۷۵. یعنی ابتدا ۳۰۰ را بر ۲ تقسیم کرده که خارج قسمت برابر با ۱۵۰ می‌شود. سپس ۱۵۰ را بر ۲ تقسیم کرده که حاصل ۷۵ است. این امر به این معنی است که در ۳۰۰، تعداد ۷۵ دسته چهارتایی وجود دارد.

اگر یکی از آن ها را کم کنیم، یعنی ۴ واحد یا یک دسته ۴ تایی از ۳۰۰ کم کنیم به ۲۹۶ خواهیم رسید. پس خارج قسمت ۲۹۶ بر ۴ برابر است با ۷۴. یعنی یک دسته ۴ تایی باید از تقسیم ۳۰۰ بر ۴ کم کنیم.

$$\large 296 \div 4 = 74$$

در آخرین گام هم باید ۷۴ را بر ۲ تقسیم کنیم. این بار هم از کسر کمک می‌گیریم.

$$\large \dfrac{74}{2} = \dfrac{ 70 + 4} {2} = \dfrac{70}{2} + \dfrac{4}{2} =  35 + 2 = 37$$

در نهایت مشخص می‌شود که حاصل تقسیم ۲۹۶۰ بر ۸۰ برابر است با ۳۷.

یک راه حل سریع‌تر نیز برای انجام این کار وجود دارد. بعد از تقسیم ۲۹۶۰ بر ۱۰ به تقسیم ساده‌تر زیر خواهیم رسید.

$$\large 296 \div 8$$

از آنجایی که رقم یکان یعنی ۶ از مقسوم علیه کوچکتر است به راحتی عمل جداسازی یا تفکیک را انجام داده و تقسیم را پی‌می‌گیریم.

$$\large \dfrac{29}{8} =3 \dfrac{5}{8}$$

حاصل صورت کسر سمت راست یعنی ۵ را به عنوان دهگان در نظر گرفته و در کنار ۶ قرار می‌دهیم. حاصل عدد ۵۶ است که باید بر ۸ تقسیم شود. با توجه به جدول ضرب می‌دانیم که نتیجه تقسیم برابر با ۷ خواهد بود. در نتیجه خارج قسمت برابر است با ۳۷ که دهگان آن از عدد صحیح تقسیم قبلی و یکان آن از تقسیم باقی‌مانده بر ۸ بدست آمده است.

مثال ۶

حاصل تقسیم ۷۳۸۰ بر ۶۰ را به صورت ذهنی بدست می‌آوریم.

$$\large 7380 \div 60$$

ابتدا با توجه به صفر بودن یکان هر دو عدد، آن‌ها را حذف می‌کنیم و تقسیم زیر را مبنا قرار می‌دهیم.

$$\large 738 \div 6$$

ابتدا ۶ را به صورت تجزیه به عامل‌های اول (یعنی حاصل‌ضرب ۲ در ۳) می‌نویسیم. در نتیجه تقسیم را به شکل زیر نمایش می‌دهیم.

$$\large \dfrac{738}{2 \times 3 } = \dfrac{ 738}{2}\times {1}{3}$$

از آنجایی که ۷۳۸ زوج است می‌دانیم که بر ۲ بخش‌پذیر است. در این قسمت عمل تقسیم بر ۲ را به شکل زیر نمایش می دهیم.

$$\large \dfrac{738}{2} = \dfrac{700}{2} + \dfrac{30}{2}+ \dfrac{8}{2} = 350 + 15 + 4 = 369$$

حال این عدد را بر ۳ تقسیم می‌کنیم. واضح است که هر یک از ارقام (یکان، دهگان و صدگان) از ۳ بزرگتر و مضارب ۳ هستند. در نتیجه داریم:

$$\large \dfrac{369}{3} = \dfrac{300}{3} + \dfrac{60}{3}+ \dfrac{9}{3} = 100 + 20 + 3 = 123$$

در نتیجه خارج قسمت تقسیم عدد ۷۳۸۰ بر ۶۰، عدد ۱۲۳ خواهد بود.

اتحادهای جبری و عمل تقسیم ذهنی و سریع

اتحادهای جبری و ریاضیاتی، تساوی‌هایی هستند که به راحتی به خاطر سپرده می‌شوند و انجام عملیات مختلف بخصوص ضرب را سریع‌تر می‌کنند. از آنجایی که تقسیم، عکس عمل ضرب است، از اتحادها برای انجام عمل تقسیم نیز می‌توان استفاده کرد. شاید اتحاد مزدوج بیشترین استفاده را در این بین داشته باشد.

اگر $$a$$  و $$b$$ دو عدد حقیقی باشند، اتحاد مزدوج به صورت زیر نوشته خواهد شد.

$$\large ( a - b ) ( a + b ) = a^2 - b^2$$

حال اگر یکی از جمله‌های سمت چپ را به سمت راست تساوی تقسیم کنیم، نتیجه به شکل‌های زیر خواهد بود.

$$\large ( a - b )  = \dfrac{ (a^2 - b^2) }{( a + b ) }$$

$$\large ( a + b ) = \dfrac{ (a^2 - b^2) } { (a - b ) }$$

این تساوی‌ها برای تقسیم اعداد صحیح نیز به کار خواهد رفت. به مثال‌هایی در این زمینه توجه کنید.

مثال ۷

نتیجه تقسیم زیر را به کمک اتحادها انجام می‌دهیم.

$$\large \dfrac{49-25}{12} = \dfrac{ (7^2 - 5^2) }{ (7 + 5)}= (7 - 5 ) = 2$$

به همین ترتیب می‌توانیم تقسیم دیگری نیز ترتیب دهیم.

$$\large \dfrac{49-25}{2} = \dfrac{ (7^2 - 5^2) }{ (7 - 5)}= (7 + 5 ) = 12$$

مثال ۸

براساس خواصی که برای ضرب اعداد بین ۱۰ تا ۱۵ در خودشان داریم، عمل تقسیم زیر را انجام می‌دهیم.

$$\large \dfrac{169-121}{2} = \dfrac{ (13^2 - 11^2) }{ (13 - 11)}= ( 13 + 11 ) = 24$$

و همچنین

$$\large \dfrac{169 -121}{24} = \dfrac{ ( 13^2 - 11^2) }{ ( 13 + 11 )}= ( 13 - 11 ) = 2$$

استفاده از الگوریتم در تقسیم ذهنی و سریع

همانطور که در نوشتار دیگر از مجله فرادرس با نام الگوریتم تقسیم اعداد — از صفر تا صد خواندید، عمل تقسیم دارای الگوریتم‌های مختلفی است. در اینجا هم می‌توانیم برای انجام تقسیم ذهنی از این الگوریتم‌ها استفاده کنیم.

معمولا هنگام انجام عمل تقسیم ذهنی و سریع، احتیاج به یک حدس اولیه برای نتیجه تقسیم داریم. شاید این حدس یا حدودی که برای نتیجه تقسیم در نظر می‌گیریم ما را به نتیجه نهایی نزدیک‌تر کند. مثال زیر گام‌های مربوط به تقسیم ذهنی و سریع توسط الگوریتم تقسیم را نشان می‌دهد.

مثال ۹

فرض کنید قرار است که ۲۵۶ را بر ۸ تقسیم کنیم. در این بین از ضرب کمک گرفته تا محدوده نتیجه را مشخص کنیم. معمولا برای پیدا کردن نتیجه یا خارج قسمت تقسیم این دو عدد گام‌های زیر را برمی‌داریم.

گام ۱: اگر ۸ را در ۱۰ ضرب کنیم، حاصل‌ضرب ۸۰ خواهد بود و اگر آن را در ۱۰۰ ضرب کنیم، به مقدار ۸۰۰ خواهیم رسید. واضح است که به علت سادگی ضرب عدد در ۱۰ یا توان‌های آن مقادیر ۸۰ و ۸۰۰ را انتخاب کرده‌ایم.

همانطور که می‌بینید عدد ۲۵۶ در بین دو مقدار ۸۰ و ۸۰۰ قرار گرفته است. در نتیجه خارج قسمت تقسیم ۲۵۶ بر ۸ نیز بین دو عدد ۱۰ و ۱۰۰ خواهد بود. پس خارج قسمت یک عدد دو رقمی است.

گام ۲: این بار مضاربی از ۱۰ که به ۲۵۶ نزدیک‌تر هستند را امتحان می‌کنیم. برای مثال اگر ۳۰ را در ۸ ضرب کنیم، حاصل‌ضرب برابر با ۲۴۰ خواهد بود. ولی حاصل‌ضرب ۴۰ در ۸ برابر با ۳۲۰ می‌شود. در نتیجه خارج قسمت یا نتیجه تقسیم ۲۵۶ بر ۸ در بازه ۳۰ تا ۴۰ قرار دارد.

گام ۳: حال فاصله ۲۴۰ تا ۲۵۶ را محاسبه می‌کنیم. این تفاضل برابر با ۱۶ است. مشخص است که در ۱۶، به تعداد ۲ دسته ۸ تایی وجود دارد. پس کافی است که ۳۰ را ۲ با جمع کرده، تا نتیجه تقسیم بدست آید.

$$\large 256 \div 8 = 32$$

همین عملیات و گام‌ها را می‌توانیم توسط یک الگوریتم پیاده‌سازی نماییم. به این ترتیب یک روش مشخص برای پیدا کردن خارج قسمت عمل تقسیم بدست می‌آید. به مثال‌ دیگری در این زمینه توجه کنید.

مثال ۱۰

خارج قسمت تقسیم ۱۰۱۲ را بر ۷ به شیوه الگوریتمی انجام و گام‌ها را مشخص‌تر می‌کنیم

گام ۱: یک دامنه برای جواب یا خارج قسمت تقسیم، پیدا می‌کنیم.

$$\large 7 \times 10 = 70$$

$$\large 7 \times 100 = 700$$

$$\large 7 \times 1000 = 7000$$

از آنجایی که ۱۰۱۲ در بازه ۷۰۰ و ۷۰۰۰ قرار دارد، خارج قسمت نیز بین ۱۰۰ تا ۱۰۰۰ خواهد بود. پس حاصل تقسیم، عددی سه رقمی است.

گام ۲: نزدیک‌ترین عددی سر رقمی که مضرب ۷ و ۱۰۰ بوده و به ۱۰۱۲ نزدیک است کدام است؟ به نظر می‌رسد این عدد می‌تواند همان ۷۰۰ باشد. در این گام مشخص است که ۱۰۰ بخشی از نتیجه تقسیم خواهد بود.

گام ۳: فاصله بین ۷۰۰ تا ۱۰۱۲ برابر است با ۳۱۲، حال عملیات تقسیم را برای اعداد ۳۱۲ و ۷ تکرار می‌کنیم.

گام ۱ (تکراری): یک دامنه جواب برای تقسیم ۳۱۲ بر ۷ بدست می‌آوریم.

$$\large 7 \times 10 = 70$$

$$\large 7 \times 100 = 700$$

از آنجایی که ۳۱۲ در فاصله ۷۰ تا ۷۰۰ قرار دارد، پس نتیجه تقسیم باید در بین اعداد ۱۰ تا ۱۰۰ قرار بگیرد و یک عدد دو رقمی خواهد بود.

گام ۲ (تکراری): عدد دو رقمی که ضرب آن در ۱۰ و ۷ نزدیک‌ترین عدد به ۳۱۲ باشد عدد ۴۰ است زیرا ۲۸۰ = ۷ × ۱۰ × ۴.

گام ۳ (تکراری): فاصله این عدد یعنی ۲۸۰ تا ۳۱۲ برابر است با ۳۲ که در آن ۴ دسته ۷ تایی قرار دارد و ۴ واحد نیز باقی‌مانده خواهد داشت.

عملیات تقسیم به پایان رسیده و نتیجه تقریبی تقسیم مطابق با تصویر زیر حاصل می‌شود.

$$\large 7 \times 100 = 700$$

$$\large + 7 \times 40 = 280$$

$$\large + 7 \times 4 = 28 \;\;$$

$$\large ---------------------------------------$$

$$\large 7 \times 144 = 1008$$

که در انتها ۴ واحد نیز باقی‌مانده خواهد داشت. در نتیجه حاصل تقسیم ۱۰۱۲ بر ۷ را به صورت زیر نمایش می‌دهیم.

$$\large 1012 \div 7 = 144 \tfrac{4}{7}$$

خلاصه و جمع‌بندی

در این نوشتار به بررسی تقسیم ذهنی و سریع پرداختیم. از آنجایی که می‌توان عمل تقسیم را عکس عمل ضرب در نظر گرفت، استفاده از اتحادهای ریاضی، می‌توانند بسیاری از عملیات تقسیم را هم برایمان ساده‌ کرده و سرعت انجام محاسبات را بهبود بخشند. البته بیشترین استفاده را می‌توان از اتحاد مزدوج در انجام عملیات تقسیم برد. به همین خاطر بهتر است حالت‌های مختلف آن را نیز به خاطر سپرد. این گونه محاسبات در متن به کمک مثال‌هایی گنجانده شده است.

با استفاده از این نوشتار و آموزش معرفی شده قادر به انجام سریع محاسبات ذهنی چهار عملی اصلی خواهید بود و کارایی محاسبات ذهنی را به رخ دیگران بکشید و ذهنتان را فعال و پویا نگه دارید.

یکی از ابزارهایی که برای محاسبه چهار عمل اصلی مناسب است و قدرت ذهنی را هم تقویت می‌کند، چرتکه است. پیشنهاد می‌کنم به مطلبی با عنوان آموزش چرتکه --- به زبان ساده در مجله فرادس هم سری بزنید.