انواع مدار الکتریکی چیست؟ – به زبان ساده

مدار الکتریکی، مجموعه‌ای از اجزای الکتریکی است که برای ذخیره، انتقال و تبدیل انرژی الکتریکی به کار می‌رود. انواع مدار الکتریکی چیست شامل دسته‌بند‌ی‌های متفاوتی می‌شود که در این مقاله مورد بحث قرار خواهد گرفت اما از میان آن‌ٰها که بیشتر در کتاب‌های درسی صحبت می‌شود مدارهای متوالی و موازی هستند. یک مدار الکترونیکی از اجزای الکترونیکی مجزا مانند مقاومت‌ها، ترانزیستورها، خازن‌ها، سلف‌ها و دیودها تشکیل شده است که توسط سیم‌های رسانا یا مسیرهایی که جریان الکتریکی می‌تواند از آن‌ها عبور کند، به هم متصل می‌شوند و در ادامه این مقاله به توضیح مختصر در مورد هر یک از این مدارها می‌پردازیم.

مدارهای الکتریکی به سبب کاربردهای متفاوت‌شان انواع مختلفی دارند و به شیوه‌های مختلف می‌توان آن‌ها را دسته‌بندی کرد. به عنوان مثال جریان برقی که در منازل استفاده می‌شود از نوع متناوب است و جهت جریان به طور مداوم در حال تغییر است؛ بنابراین باید مدار در این وضعیت از نوع موازی باشد، در حالی که در مدار متوالی، جریان از تمام اجزا عبور می‌کند و از این رو مدارهای متوالی برای منازل استفاده نمی‌شوند، لذا برای هر یک از موارد از مدار مخصوص به خود استفاده می کنیم که در ادامه توضیح داده خواهد شد.

دسته‌بندی انواع مدار الکتریکی چیست

دسته‌بندی انواع مدارهای الکتریکی در زیر فهرست شده است که در ادامه این مطلب به معرفی هر یک از آنان خواهیم پرداخت.

1. متوالی، موازی، ترکیبی و ستاره - مثلث
2. خطی و غیرخطی
3. یک طرفه و دو طرفه
4. مرتبه اول و مرتبه دوم
5. آنالوگ و دیجیتال
6. مدار باز، بسته و اتصال کوتاه
7. متناوب (AC) و مستقیم (DC)
8. طبقه‌بندی براساس اجزا

۱. مدار متوالی، موازی، ترکیبی و ستاره - مثلث

در این بخش به توضیح انواع مدارهای متوالی، موازی، ترکیبی و ستاره - مثلث پرداخته می‌شود و مثال‌های نیز بیان می‌کنیم.

مدار متوالی

یک مدار متوالی یا «سری» (Series) به شکلی است که اجزای آن پشت سر یکدیگر قرار گرفته و به پایانه مثبت و منفی باتری متصل هستند. در یک مدار متوالی، تنها یک مسیر برای عبور جریان وجود دارد و در نتیجه جریان یکسان از تمام اجزا مدار عبور می‌کند. به عبارت دیگر جریان عبوری از همه عناصر یکسان خواهد بود ولی ولتاژ بین آن‌ها تقسیم می‌شود. به شکل زیر توجه کنید:

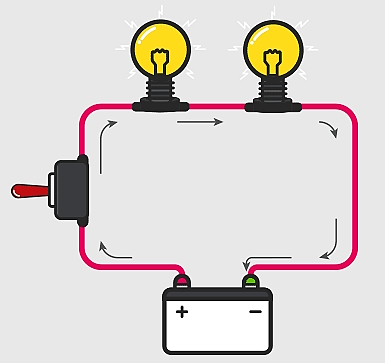
اگر در مدار مقاومت وجود داشته باشد، با به کار بردن قانون اهم می‌توان مقاومت کل (معادل) را محاسبه کرد.

$$R_{total}=\sum_i R_i$$

بنابراین مقاومت کل در یک مدار متوالی برابر جمع جبری هر یک از مقاومت‌ها است.

ظرفیت خازن کل (معادل) مطابق فرمول زیر محاسبه می‌شود:

$$\frac{1}{C_{total}}=\sum_i \frac{1}{C_{i}}$$

مثال اول برای مدار متوالی

در مثال ساده زیر منبع تغذیه مستقیم ۵ ولت است می‌خواهیم جریان را در مقاومت شکل زیر حساب کنیم.

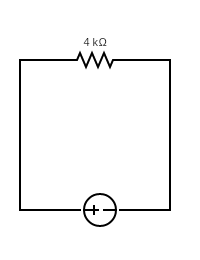
با استفاده از قانون اهم می‌توانیم معادله زیر را بنویسیم:

$$V=I\times R$$

$$I=\frac{V}{R}=\frac{5}{4}=1.25mA$$

مدار موازی

یکی دیگر از انواع مدارهای الکتریکی، مدار موازی (Parallel) است. در این نوع مدارها، اجزا الکترونیکی همان‌طور که از نام این نوع اتصال پیداست، به صورت موازی بسته می‌شوند و انشعاب‌های زیادی در این نوع مدار وجود دارد. (در تمام مدارهای موازی حداقل دو انشعاب مشاهده می شود). به عبارت دیگر ولتاژ عبوری از میان عناصر یکسان است ولی جریان بین آن‌ها تقسیم می‌شود. به شکل زیر توجه کنید:

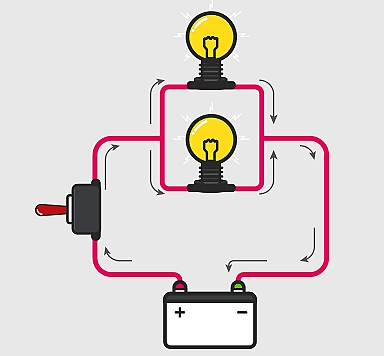
بنابراین جریان منبع تغذیه برابر با جمع جریان گذرنده از تک‌تک مولفه‌های موجود در مدار خواهد بود. محاسبه مقاومت کل و ظرفیت کل خازن هم برعکس مدار متوالی است.

مقاومت کل (معادل) در مدار موازی به شکل زیر است:

$$\frac{1}{R_{total}}=\sum_i \frac{1}{R_{i}}$$

و ظرفیت خازن کل (معادل) در مدار موازی:

$$C_{total}=\sum_i C_i$$

مثال اول برای مدار موازی

در مثال ساده زیر یک منبع تغذیه مستقیم با ۵ ولت است و می‌خواهیم جریان کل را در مدار شکل زیر حساب کنیم.

برای حل این مثال ابتدا باید مقاومت معادل را حساب کرد.

$$\frac{1}{R_{total}}=\sum (\frac{1}{R_{1}}+\frac{1}{R_{2}})=\frac{1}{4}+\frac{1}{5}=\frac{9}{20}$$

در نتیجه مقاومت کل برابر است با:

$${R_{total}}=2.22 k\Omega$$

اکنون می‌توانیم با استفاده از قانون اهم جریان کل را حساب کنیم.

$$V=I\times R$$

$$I=\frac{V}{R}=\frac{5}{2.22}=2.25mA$$

مدار ترکیبی

در بسیاری از مدارهای الکتریکی، برخی اجزا در مدار به صورت متوالی و برخی دیگر به صورت موازی به یکدیگر متصل شده‌اند که به اصطلاح مدار ترکیبی (Compound) گفته می‌شود. در تحلیل این نوع از مدارهای پیچیده باید مدار را به قسمت‌های ساده‌تر یعنی متوالی و موازی تبدیل کرد تا بتوان محاسبات مربوطه را انجام داد.

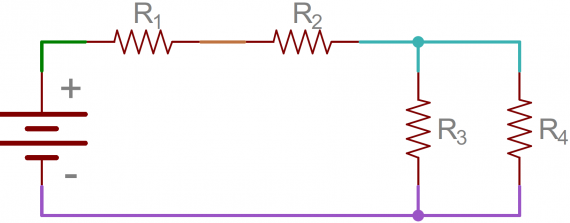
مثال اول برای مدار ترکیبی

در مدار شکل زیر که ترکیب مقاومت متوالی و موازی است به منبع تغذیه مستقیم ۵ ولت متصل است، می‌خواهیم جریان کل مدار را حساب کنیم.

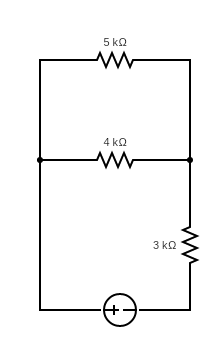
برای حل این مثال ابتدا مقاومت معادل برای مقاومت‌های ۴و ۵ اهمی را به صورت موازی بدست می‌آوریم و سپس حاصل را با مقاومت ۳ اهمی به صورت معادل می‌گیریم.

$$\frac{1}{R_{total}}=\sum (\frac{1}{R_{1}}+\frac{1}{R_{2}})=\frac{1}{4}+\frac{1}{5}=\frac{9}{20}$$

$${R_{1}}=2.22 k\Omega$$

$$R_{total}=2.22+3=5.22k\Omega$$

اکنون می‌توانیم با استفاده از قانون اهم جریان کل را حساب کنیم.

$$V=I\times R$$

$$I=\frac{V}{R}=\frac{5}{5.22}=0.95mA$$

مدار ستاره و مثلث

مدار ستاره و مثلث و ترکیب آن یعنی «ستاره و مثلث استارتر» (Star - Delta Starter) یک مدار کنترل الکتریکی است که برای راه‌اندازی و کنترل سرعت موتورهای القایی سه فاز استفاده می‌شود. این استارتر به طور گسترده‌ای در صنایع مختلف مثل موتورهای با توان بالا استفاده می‌شود. مدار ستاره - مثلث با اتصال اولیه سیم پیچ‌های موتور به صورت ستاره و سپس تغییر آن به مثلث کار می‌کند. این تغییر اتصال باعث کاهش جریان راه‌اندازی موتور می‌شود که به جلوگیری از آسیب به موتور و خطوط برق کمک می‌کند. در تصویر زیر، تصاوت بین مدارهای ستاره (ستاره‌ای) و مثلث (مثلثی) نشان داده شده است.

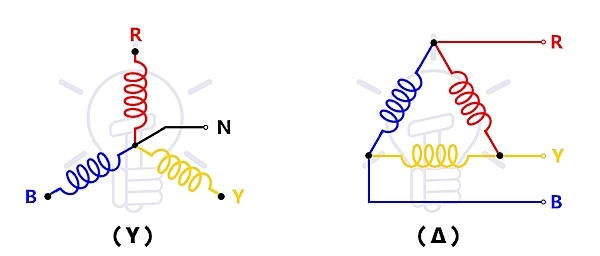
مثال اول مدار ستاره - مثلث

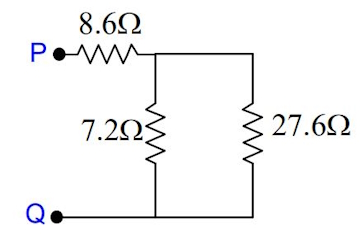
با توجه به شکل زیر مقاومت بین نقاط P و Q را محاسبه کنید.

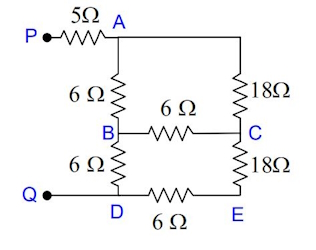
در مدار شکل فوق، بین نقاط A، B و C یک اتصال دلتا با سه مقاومت $$6Ω$$، $$6Ω$$ و $$18Ω$$ موجود است که آن‌ها را با معادلات زیر به اتصال ستاره تبدیل می‌کنیم.

$$R_A = \frac{ R_{AB} \times R_{AC}}{\sum R_{AB}}$$

$$R_A =\frac{6\times18}{30}= 3.6\Omega$$

$$R_B =\frac{6\times6}{30}= 1.2\Omega$$

$$R_C =\frac{6\times18}{30}= 3.6\Omega$$

سه دسته مقاومت‌های متوالی می‌توان در شکل مشاهد کرد یعنی دسته اول در سمت چپ $$5Ω$$ و $$3.6Ω$$ و $$1.2Ω$$ و $$6Ω$$ و دسته دوم در سمت راست $$3.6Ω$$ و $$18Ω$$ و $$6Ω$$ به ترتیب متوالی هستند.

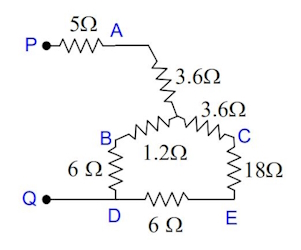
اکنون مقاومت‌های $$7.2Ω$$ و $$27.6Ω$$ موازی هستند و مقاومت معادل این دو با مقاومت $$8.6Ω$$ متوالی است. بنابراین مقاومت معادل بین نقاط P و Q به شکل زیر خواهد شد:

$$ R_{PQ} = 8.6 + \frac{7.2 \times 27.6}{7.2 + 27.6} = 8.6 + 5.71 = \mathbf{14.31 \, \Omega} $$

مثال دوم مدار ستاره - مثلث

در مدار شکل زیر مقاومت معادل بین دو نقطه A و B را محاسبه کنید.

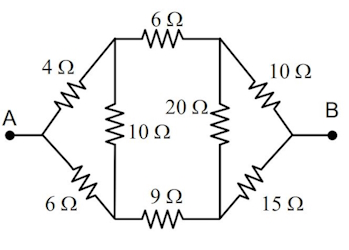
پاسخ:

ابتدا در مثلث سمت چپ و راست دلتا را به ستاره تبدیل می‌کنیم.

در مثلث سمت چپ:

$$R_A = \frac{4 \times 6}{20} = \mathbf{1.2 \, \Omega}$$

$$R_B = \frac{4 \times 10}{20} = \mathbf{2 \, \Omega}$$

$$R_C = \frac{6 \times 10}{20} = \mathbf{3 \, \Omega}$$

و در مثلث سمت راست:

$$R_A = \frac{10 \times 15}{45} = \mathbf{3.33 \, \Omega}$$

$$R_B = \frac{10 \times 20}{45} = \mathbf{4.44 \, \Omega}$$

$$R_C = \frac{20 \times 15}{45} = \mathbf{6.67 \, \Omega}$$

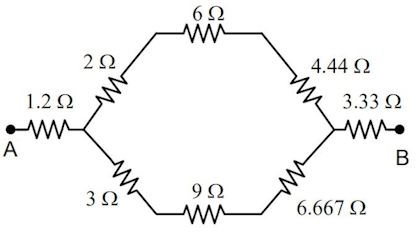
اکنون سه مقاومت در اضلاع بالای شش ضلعی و سه مقاومت پایین شش ضلعی را به صورت متوالی جمع می‌کنیم تا مدار به صورت شکل زیر تبدیل شود:

$$ R_{AB} = 1.2 \Omega + \frac{12.44 \times 18.667}{12.44 + 18.667}+3.3\Omega = 1.2\Omega + \frac{232.217}{12.44\Omega+31.187\Omega} +3.3\Omega= 1.2\Omega + 7.446\Omega + 3.3\Omega = \mathbf{11.94\Omega} $$

۲. مدارهای خطی و غیرخطی

تا اینجا با مدارهای متوالی، موازی و ترکیبی از انواع مدار الکتریکی چیست آشنا شدید در این بخش به توضیح انواع مدارهای خطی و غیرخطی پرداخته می‌شود و مثال‌های نیز بیان می‌کنیم.

مدار خطی

یکی از انواع مدارهای الکتریکی است که پارامترهای مقاومت، خازن، القاگر (سلف)، شکل موج و فرکانس و غیره در آن ثابت‌ هستند. به این معنی که پارامترهای ذکر شده با تغییر ولتاژ و جریان تغییر نمی‌کنند. اگر مداری فقط از این عناصر خطی تشکیل شده باشد، مدار به عنوان مدار خطی شناخته می شود.

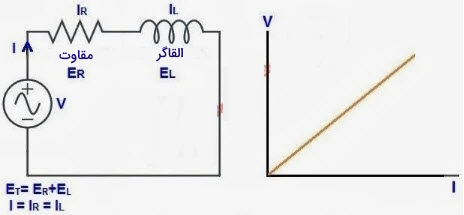
تقویت‌کننده، متمایز کننده و فیلترهای الکترونیکی خطی از نمونه‌های مدارهای خطی هستند.

مثال اول برای مدار حطی

شکل زیر را در نظر بگیرید. با توجه به مقادیر زیر می‌خواهیم زمان رسیدن جریان به ۱٫۵ آمپر با بسته شدن کلید را حساب کنیم.

$$V=10 (volt)$$

$$R=5 (ohm)$$

$$L=20 (Henrie)$$

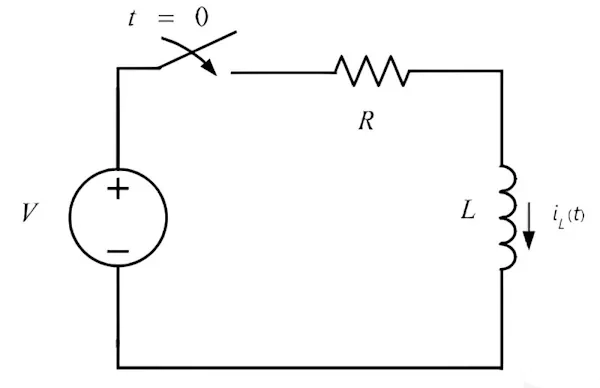
پاسخ:

برای حل این سوال از فرمول جریان در مدارهای شامل مقاومت و القاگر استفاده می‌کنیم.

$$\displaystyle{ i = \frac{V}{R}(1 - e^{(-\frac{R}{L}t)}) }$$

$$\displaystyle{ 1 - \frac{iR}{V} = e^{(-\frac{R}{L}t)} }$$

$$\displaystyle{ \ln(1 - \frac{iR}{V}) = -\frac{R}{L}t }$$

$$\displaystyle{ -\frac{L}{R} \times \ln(1 - \frac{iR}{V}) = t }$$

در نتیجه زمان $$\displaystyle{ t = 5.5 s }$$ خواهد بود.

مدار غیرخطی

برعکس مدار خطی، مدارهای غیرخطی حساسیت زیادی نسبت به نوسانات جریان و ولتاژ دارند و پارامترهای مقاومت، خازن، شکل موج و فرکانس در آن‌ها ثابت نیستند. دیودها و ترانزیستورها دو عنصر اصلی مدارهای غیرخطی هستند. از نمونه‌های دیگر می‌توان به سلف‌ها و ترانسفورماتور با هسته آهنی اشاره کرد. اگر مدار حداقل از یک عنصر غیرخطی تشکیل شده باشد، به آن مدار غیرخطی می‌گویند.

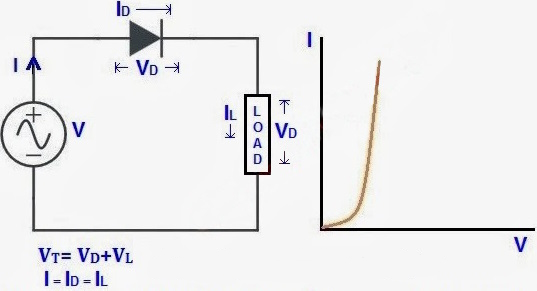
مثال اول برای مدار غیرخطی

به شکل زیر توجه کنید. در این مدار $$R_{2}=2kΩ$$، $$R_{1}=1kΩ$$ و اختلاف پتانسیل منبع تغذیه ۹ ولت و دو دیود سیلیکونی داریم. با توجه به مقادیر داده شده شدت جریان در مدار را محاسبه کنید.

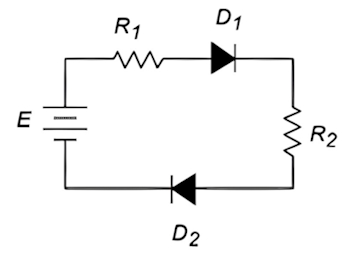
مطابق با قوانین KVL، چون این یک مدار تک‌حلقه است اختلاف پتانسیل باید با جمع افت ولتاژ مقاومت‌ها و دیودها برابر باشد. هر دو دیودها در بایاس مستقیم قرار دارند (جریان متعارف وارد آند می‌شود). چون هر دو دیود از جنس سیلیکون هستند در نتیجه $$V_{knee1}=V_{knee2}=0.7V$$.

$$I = \frac{ E−V_{knee1} − V_{knee2}}{R_1+R_2} \nonumber$$

$$I = \frac{ 9V−0.7V−0.7V}{1k \Omega +2 k\Omega} \nonumber$$

$$I = 2.533mA \nonumber$$

توجه کنید که اگر هر کدام از دیودها برعکس بسته شود دیگر جریانی در مدار نخواهد بود.

۳. مدار یک طرفه و دو طرفه

تاکنون با مدارهای خطی و غیرخطی از انواع مدار الکتریکی چیست آشنا شدید در این بخش به توضیح انواع مدارهای یک‌طرفه و دوطرفه پرداخته می‌شود و مثال‌های نیز ارائه می‌کنیم.

مدار یک طرفه

برای درک مدارهای یک‌طرفه (Half-Wave Rectification)، خیابان‌های یک‌طرفه را به یاد بیاورید که در آن‌ها مهم‌ترین عامل، جهت حرکت است. در مدارهای یک‌‌طرفه جریان فقط در یک جهت اجازه عبور دارد که این کار توسط یکسوکننده‌های دیودی انجام می‌شود. دیود به عنوان یکسوکننده نمونه کلاسیک مدار یک‌طرفه است که در آن فقط سیکل مثبت سیگنال AC را اصلاح می‌کند تا جریان DC تولید کند اما سیکل منفی را اصلاح نمی‌کند. شکل امواج ولتاژ خروجی در مدار یک طرفه دارای بی‌نظمی زیادی است که با استفاده از خازن می‌توان آن‌ها را فیلتر کرد و کاهش داد.

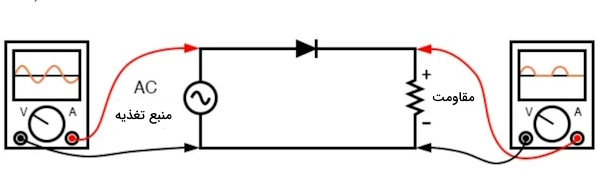
مثال اول مدار یک طرفه

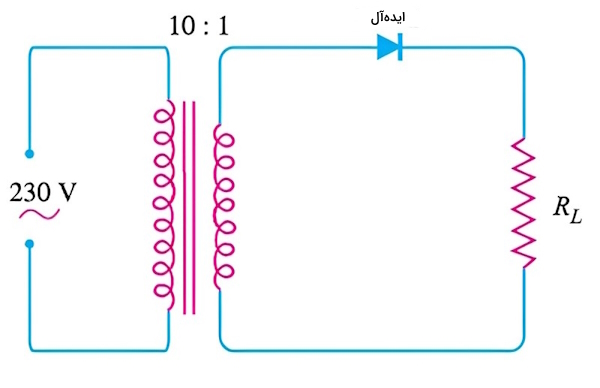
یک منبع جریان متناوب با ولتاژ ۲۳۰ ولت از طریق یک ترانسفورماتور که نسبت سیم‌پیچ آن 10:1 است به یک مدار یک طرفه متصل شده است. با توجه به شکل می‌خواهیم مقادیر زیر را حساب کنیم.

• الف. ولتاژ خروجی منبع مستقیم.
• ب. اوج ولتاژ معکوس. فرض کنید که دیود ایده‌آل هست.

پاسخ:

نسبت سیم‌پیچ اولیه ترانسفورماتور به سیم‌پیچ ثانویه آن به شکل زیر است:

$$\frac{N_{1}}{N_{2}}=10$$

ولتاژ موثر (ًR.M.S) = 230V

بیشینه ولتاژ اصلی:

$$325.3V=\sqrt{2}\times230=V_{pm}$$

بیشینه ولتاژ مدار ثانویه:

$$V_{sm}=V_{pm}\times\frac{N_{1}}{N_{2}}=325.3\times\frac{1}{10}=32.53V$$

بنابراین برای قسمت (الف) خواهیم داشت:

$$I_{dc}=\frac{I_{m}}{\pi}$$

$$V_{dc}=\frac{I_{m}}{\pi}\times R_{L}=\frac{V_{sm}}{\pi}=\frac{32.53}{\pi}=10.36V$$

در پاسخ به قسمت (ب)، در سیکل منفی منبع جریان متناوب چون دیود در بایاس معکوس قرار دارد در نتیجه هیچ جریانی عبور نمی‌کند بنابراین اوج ولتاژ معکوس در دیود برابر 32.53V است.

مثال دوم مدار یک طرفه

یک دیود کریستالی با مقاومت $$r_{f}=20Ω $$ داریم که برای یک‌سوکننده استفاده می‌شود. اگر یک منبع متناوب با ولتاژ $$v=50\sin \omega t$$ و یک مقاومت $$R_{L}=800Ω$$ در این مدار استفاده شده باشد، مطلوب است:

• الف: محاسبه مقادیر $$I_{DC}$$، $$I_{m}$$ و $$I_{rms}$$
• ب: توان ورودی منبع متناوب (AC) و توان خروجی مستقیم (DC)
• ج: ولتاژ حروجی DC
• د: بازدهی یک‌سوکننده

پاسخ:

$$v=50\sin \omega t$$

پس بیشینه ولتاژ خواهد بود:

$$V_{m}=50V$$

در قسمت (الف)

\begin{align*}I_m &= \frac{V_m}{r_f + R_L} = \frac{50}{20 + 800} = 0.061~\text{A} = 61~\text{mA} \\I_\text{rms} &= \frac{I_m}{{2}} = \frac{61~\text{mA}}{{2}} = 30.5~\text{mA} \\I_\text{dc} &= \frac{I_m}{\pi} = \frac{61~\text{mA}}{\pi} = 19.4~\text{mA}\end{align*}

در قسمت (ب)

$$a.c\ power \ input=(I_{rms})^{2}\times (r_f+R_L)=(\frac{30.5}{1000})^{2}\times(20+800)=0.763 \ watt$$

$$d.c\ power \ output=I_{dc}^{2} \times R_L=(\frac{19.4}{1000})^{2}\times(800)=0.301 \ watt$$

برای قسمت (ج)

$$d.c\ power \ voltage=I_{dc} \times R_L={19.4mA}\times800Ω=0.301 \ watt$$

برای قسمت (د) بازدهی یک‌سوکننده عبارت است:

$$\frac{0.301}{0.763}\times = 39.5\% $$

مدار دو طرفه

یکی دیگر از انواع مدارهای الکتریکی، مدار دو طرفه (Full-Wave Rectification) را می‌توان نام برد. عکس آنچه در مدارهای یک‌طرفه رخ می‌دهد را می‌توان به مدارهای دوطرفه نسبت داد که در آن‌ها جریان در هر دو جهت، اجازه عبور دارد و این نوع مدارها برای خطوط انتقال بسیار با اهمیت هستند چراکه در این نوع مدار، جهت و جای قرار گیری منبع تغذیه، چندان مهم نیست. مدار مقاومتی یک مثال ساده از مدار دوطرفه به شمار می‌رود. ولتاژ خروجی دارای امواج منظم‌تری است و به فیلتر کردن کمتری نیاز دارد به همین دلیل نسبت به مدار یک‌طرفه بیشتر رایج است.

مثال اول مدار دوطرفه

در یک مدار یک‌سوکننده دوطرفه، دو دیود داریم که مقاومت هر دو آن‌ها برابر صفر است.

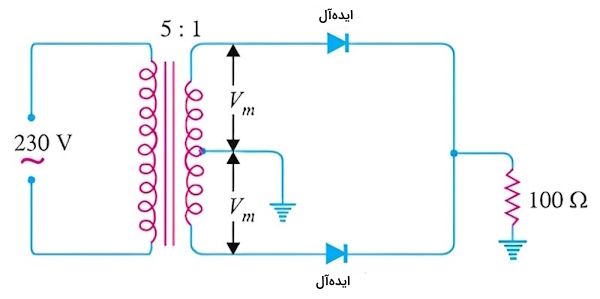
مطلوب است:

• الف: جریان خروجی dc
• ب: اوج ولتاژ معکوس
• ج: بازدهی یک‌سوکننده

پاسخ:

مطابق شکل در ترانسفورماتور، نسبت سیم‌پیچ اولیه به ثانویه به شکل زیر است:

$$\frac{N_1}{N_2} = 5 $$

$$primery \ V_{rms}=230V$$

$$secondary \ V_{rms}=230 \times 1/5 = 46V$$

بیشینه ولتاژ ثانویه (سمت راست):

$$46\times \sqrt{2}=65V$$

بیشینه ولتاژ ثانویه عبوری از هر دیود:

$$V_m=\frac{65}{2}=32.5V$$

برای قسمت (الف):

$$I_{dc}=\frac{2V_m}{\pi R_L}=\frac{2 \times 32.5}{\pi \times 100}=0.207A$$

برای قسمت (ب) اوج ولتاژ معکوس برابر بیشینه ولتاژ ثانویه است.

$$V=65volt$$

و برای قسمت (ج) بازدهی یک‌سوکننده را به صورت زیر حساب می‌کنیم:

$$\frac{0.812}{1+\frac{r_f}{R_L}}$$

از آنجا که $$r_f=0$$ بنابراین بازده برابر $$81.2\%$$ می‌شود.

مثال دوم مدار دو طرفه

در مدار شکل زیر، یک مدار یک‌سوکننده دوطرفه است که چهار دیود ایده‌آل دارد (مقاومت داخلی دیودها صفر است). مطلوب است:

الف. ولتاژ خروجی dc

ب. اوج ولتاژ معکوس

ج. فرکانس خروجی

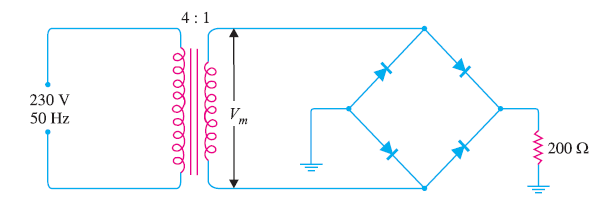
پاسخ

مطابق شکل نسبت سیم‌پیچ اولیه ترانسفورماتور به سیم‌پیچ دوم برابر است با:

$$\frac{N_1}{N_2}=4$$

ولتاژ موثر اولیه (سمت چپ):

$$primary\ V_{rms}=230v$$

ولتاژ موثر ثانویه (سمت راست):

$$secondary\ V_{rms}=230v \times \frac{N_1}{N_2}=57.5v$$

بیشینه ولتاژ در مدار ثانویه (سمت راست):

$$V_{m}=57.5\times \sqrt{2}=81.3v$$

برای قسمت (الف):

$$I_{dc}=\frac{2V_m}{\pi R_L}=\frac{2\times 81.3}{\pi \times 200}=0.26A$$

$$V_{dc}=I_{dc}\times R_L=0.26\times 200=52v$$

برای قسمت (ب): اوج ولتاژ معکوس برابر بیشینه ولتاژ مدار ثانویه یعنی $$81.3v$$ است.

قسمت (ج): در مدار یک‌سوکننده دو طرفه، دو پالس خروجی برای هر چرخه کامل جریان متناوب ورودی وجود دارد. بنابراین فرکانس خروجی دو برابر فرکانس متناوب خروجی است:

$$f_{out}=f_{in}\times 2=50 \times 2=100\ Hz$$

۴. مدار مرتبه اول و مرتبه دوم

تا اینجا با مدارهای یک‌طرفه و دوطرفه از انواع مدار الکتریکی چیست آشنا شدید در این بخش به توضیح انواع مدارهای مرتبه اول و مرتبه دوم پرداخته می‌شود و مثال‌های نیز بیان می‌کنیم.

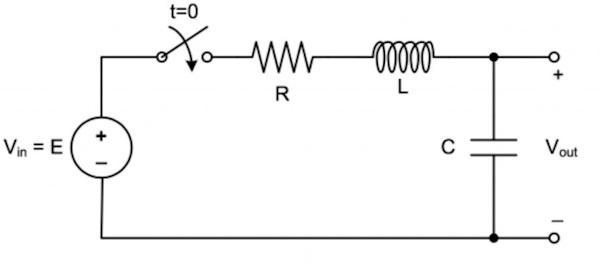
مدار مرتبه اول

تا اینجا آموختید که انواع مدار الکتریکی چیست اما انواع دیگری از دسته‌بندی هم وجود دارد. مدارهای مرتبه اول (First-Order Circuits) مدارهایی هستند که فقط یک عنصر ذخیره انرژی دارند که می‌تواند یک خازن یا سلف باشد. بنابراین می‌توان آن‌ها را با یک معادله دیفرانسیل مرتبه اول توصیف کرد. این مدارها با پاسخ نمایی آن‌ها به تغییرات ولتاژ یا جریان شناسایی می‌شوند. این نوع مدار دارای دو نوع RL و RC است. از کاربردهای مدار مرتبه اول می‌توان به موارد زیر اشاره کرد:

• فیلتر کردن: فیلترها برای جدا کردن فرکانس‌های مختلف یک سیگنال استفاده می‌شوند.
• رگولاتور ولتاژ: برای ثابت کردن ولتاژ خروجی مورد استفاده قرار می‌گیرد حتی اگر ولتاژ ورودی به طور مداوم تغییر کند.
• مدارهای شارژ و تخلیه (دشارژ): این مدارها برای شارژ یا تخلیه خازن یا القاگر به میزان معینی از ولتاژ یا جریان طراحی شده‌اند.

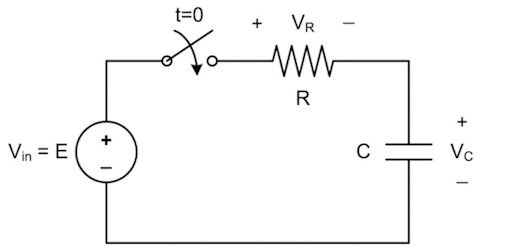
مثال اول برای مدار مرتبه اول

ولتاژ $$V_{\circ}(t)$$ را تعیین کنید.

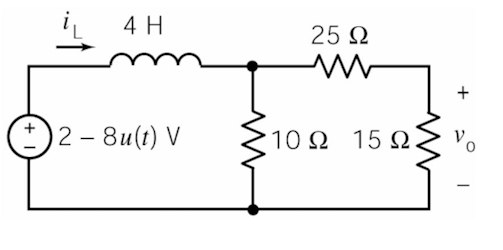
پاسخ:

در مدارهای مرتبه اول که شامل القاگر هستند ابتدا باید جریان القاگر یعنی $$I_{L}(t)$$ را تعیین کنیم.

حالت اول $$t<0$$

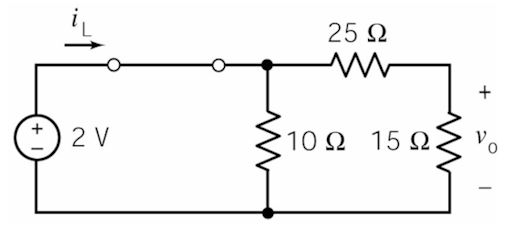
قبل از اینگه منبع ولتاژ در $$t=0$$ ناگهان تغییر کند، مدار در حالت پایدار قرار دارد. مقدار منبع ولتاژ در حالت پایدار $$2V$$ است، در نتیجه القاگر مانند اتصال کوتاه عمل می‌کند.

$$ i_L(0) = \frac{2}{10\parallel (25+15)} = \frac{2}{8} = 0.25 \, A $$

حالت دوم $$t>0$$

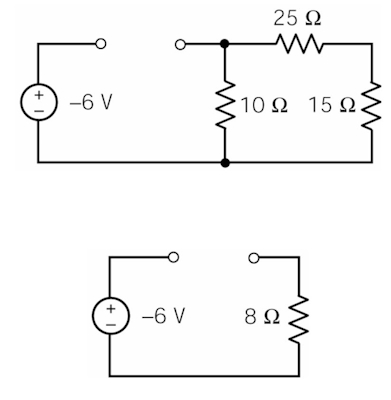
بعد از $$t=0$$ منبع ولتاژ به طور ناگهانی تغییر می‌کند و مدار در حالت ناپایداری قرار می‌گیرد. برای قسمتی از مدار که القاگر در آن قرار دارد تحلیل مدار نورتون را انجام می‌دهیم.

مقاومت معادل و ولتاژ به شکل زیر خواهند بود:

$$R_{t}=8Ω$$

$$v_{oc}=-6V$$

بنابراین جریان به شکل زیر است:

$$i_{sc}=\frac{-6}{8}=-0.75A$$

ثابت زمانی برای مدار مرتبه اول که شامل القاگر است به شکل زیر است:

$$\tau=\frac{L}{R_{t}}$$

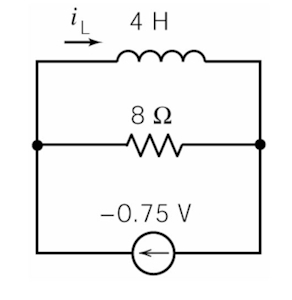
بنابراین:

$$\tau=\frac{L}{R_{t}}=\frac{4}{5}=0.5s$$

$$a=\frac{1}{\tau}=2\frac{1}{s}$$

جریان در القاگر به صورت زیر است:

$$ i_L(t) = i_{sc} + (i(0) - i_{sc})e^{-at} = -0.75 + (0.25 - (-0.75))e^{-2t} = -0.75 + e^{-2t} \text{ for } t \geq 0 $$

اکنون ولتاژ خروجی را به عنوان تابعی از منبع ولتاژ و جریان القاگر می‌نویسیم. از تقسیم جریان خواهیم داشت:

$$ i_R = \frac{10}{10 + (25+15)} i_L = 0.2i_L $$

همچنین از قانون اهم نیز استفاده می‌کنیم.

$$V_0 = 15i_R = 3i_L $$

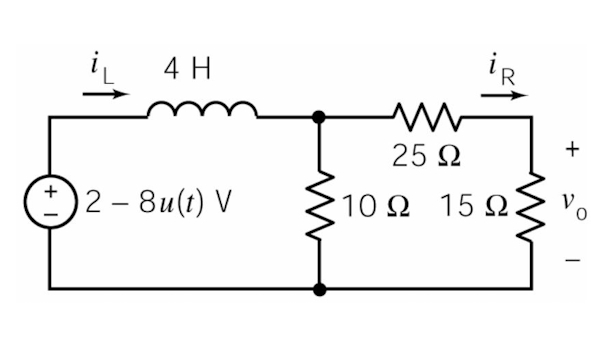
ولتاژ خروجی به صورت زیر خواهد شد:

$$v_{0}(t) = -2.25 + 3e^{-2t} \text{ for } t \geq 0$$

مدار مرتبه دوم

در حوزه مدارهای الکتریکی، مدارهای مرتبه دوم (Second-Order Circuits) شامل مدارهایی هستند که شامل دو عنصر ذخیره انرژی یعنی دو خازن یا دو سلف، یا ترکیبی از یک خازن و یک سلف هستند. این مدارها در مقایسه با مدارهای مرتبه اول پاسخ پیچیده‌تری نسبت به تغییرات ولتاژ یا جریان نشان می‌دهند، که با رفتار نوسانی یا نوسانی میرا شناسایی می‌شوند.

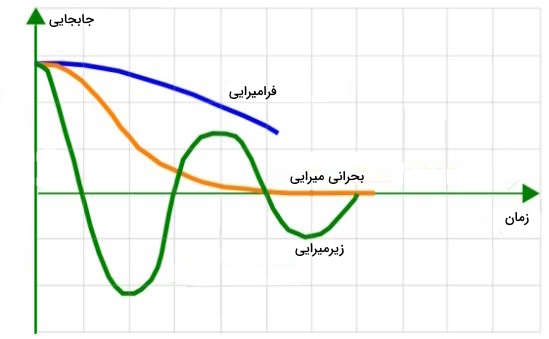
مدارهای مرتبه دوم توسط معادلات دیفرانسیل مرتبه دو توصیف می‌شوند که پاسخ پیچیده‌تری نسبت به مدارهای مرتبه اول دارند. رفتار آن‌ها را بر اساس ریشه‌های معادله دیفرانسیل درجه دوم طبقه‌بندی می‌کنند.

• «فرامیرایی» (Over damped): در این حالت ریشه‌های معادله دیفرانسیل حقیقی و متمایز هستند در نتیجه پاسخ مدار غیرنوسانی است و جریان یا ولتاژ مدار به صورت نمایی افت می‌کند.
• «بحرانی میرایی» (Critically Damped): در این حالت ریشه‌های معادله دیفرانسیل حقیقی و یکسان هستند پس در نتیجه میرایی یک نوسانگر باعث می‌شود تا با سرعت به موقعیت تعادل خود بازگردد بدون اینکه در اطراف این موقعیت نوسان کند.
• «زیرمیرایی» (Under damped): ریشه‌های معادله مختلط و مزدوج یکدیگر هستند که منجر به پاسخ نوسانی کنترل شده خواهد شد. ولتاژ یا جریان مدار بین مقادیر بیشینه و کمینه تغییر می‌کند قبل از اینکه به حالت پایدار نزدیک شود.

مثال اول برای مدار مرتبه دوم

در یک مدار RLC موازی با مقادیر $$C=100mF$$ و $$L=1H$$، مقدار مقاومت باید چقدر باشد تا فرکانس‌های طبیعی مدار $$x_{1}=-2s^{-1}$$ و $$x_{2}=-5s^{-1}$$ باشد؟

در معادله دیفرانسیل استاندارد مرتبه دوم، یعنی $$v''+2\alpha v'+\omega^{2}_{\circ}v=0$$ داریم:

$$x_{1}+x_{2}=-2\alpha=-7$$

$$\omega^{2}_{\circ}=x_{1}\times x_{2}=10$$

بنابراین چون برای مدار موازی $$\alpha = \frac{1}{2RC}$$ داریم:

$$R = \frac{1}{2C\alpha}=\frac{1}{7\times0.1}=1.43Ω$$

۵. مدار آنالوگ و دیجیتال

تاکنون با مدارهای مرتبه اول و مرتبه دوم از انواع مدار الکتریکی چیست آشنا شدید در این بخش مدارهای آنالوگ و دیجیتال معرفی خواهیم کرد.

مدار آنالوگ

مدارهای الکترونیکی آنالوگ مدارهایی هستند که در آن‌ها جریان یا ولتاژ ممکن است به طور پیوسته با زمان تغییر کند تا با اطلاعات موجود مطابقت داشته باشد. تحلیل مدار آنالوگ از قوانین کیرشهف استفاده می‌کند به این صورت که تمام جریان‌های در یک گره (جایی که سیم‌ها با هم برخورد می‌کنند) و ولتاژ در اطراف یک حلقه بسته صفر است. سیم‌ها به طور معمول به عنوان اتصال ایده‌آل بدون مقاومت در نظر گرفته می‌شوند.

مدار دیجیتال

در مدارهای الکترونیکی دیجیتال، سیگنال‌های الکتریکی مقادیر گسسته‌ای را اتخاذ می‌کنند تا مقادیر منطقی و عددی را نشان دهند. این مقادیر، اطلاعات پردازش شده را نشان می‌دهند. در اکثر موارد، کدگذاری دودویی (در مبنای ۲) مورد استفاده قرار می‌گیرد: یک ولتاژ (یه طور معمول ولتاژ مثبت‌تر) نمایانگر 1 در مبنای دو را نشان می‌دهد و ولتاژ دیگری (به طور معمول یک ولتاژ در نزدیکی پتانسیل زمین، 0 ولت) نمایانگر 0 در مبنای دو را نشان می‌دهد. مدارهای دیجیتال از ترانزیستورها به‌طور گسترده استفاده می‌کنند که به هم متصل می‌شوند تا دروازه‌های منطقی (Logic Gates) را ایجاد کنند که منطق بولین (Boolean Logic) را ارائه می‌دهند.

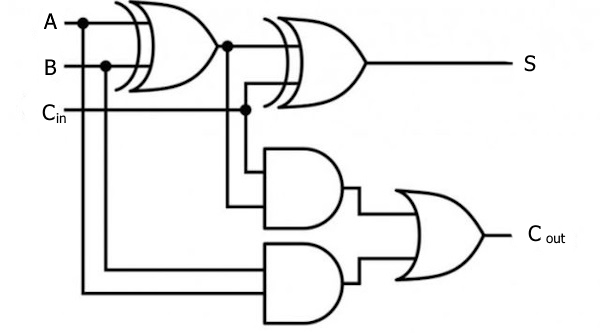
البته در بسیاری از لوازم الکترونیکی ترکیبی از مدارهای انالوگ و دیجیتال استفاده می‌شود.

۶. مدار باز، بسته و اتصال کوتاه

تا اینجا با مدارهای آنالوگ و دیجیتال از انواع مدار الکتریکی چیست آشنا شدید در این بخش به معرفی انواع مدارهای باز،بسته و اتصال کوتاه پرداخته خواهد شد.

مدار باز

در مدار الکتریکی، اگر در مسیر عبور جریان قطع شود، به آن مدار باز (Open Circuit) می‌گویند. یک کلید باز یا یک فیوز سوخته جریان جریان را قطع می‌کند.

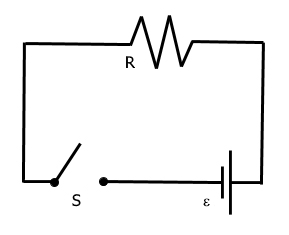
مدار بسته

مدار بسته (Closed Circuit) به مداری گفته ‌شود که تمام جریان‌ از جایی که شروع شده دوباره به همان نقطه برگردد و هیچ مانعی برای قطع جریان وجود نداشته باشد.

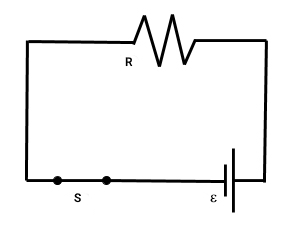
مدار اتصال کوتاه

اتصال کوتاه (Short Circuit) زمانی رخ می‌دهد که یک مسیر (سیم) با کمترین مقاومت (به طور معمول به اشتباه) به دو سر یک اتصال وصل شود. برای مثال در شکل زیر مقاومت نشان داده شده در مسیر جریان اصلی است و سیم منحنی دور آن اتصال کوتاه است. جریان از مسیر اصلی خود منحرف می‌شود که گاهی اوقات منجر به آسیب خواهد شد. سیم با ارائه مسیری با مقاومت کمتر برای جریان، مقاومت را کوتاه می‌کند.

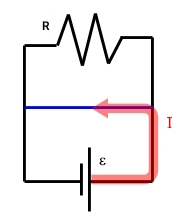
۷. مدار متناوب (AC) و مستقیم (DC)

تا اینجا با مدارهای باز، بسته و اتصال کوتاه از انواع مدار الکتریکی چیست با مثال آشنا شدید، در این بخش به معرفی انواع مدارهای متناوب و مستقیم پرداخته می‌شود و مثال‌های نیز ارائه می‌کنیم.

مدار با منبع متناوب

به طور ساده اگر منبع تغذیه اصلی در مدار متناوب باشد، به آن مدار متناوب می‌گویند. البته برای حل اینگونه مدارها لازم است با اعداد مختلط آشنایی داشته باشید.

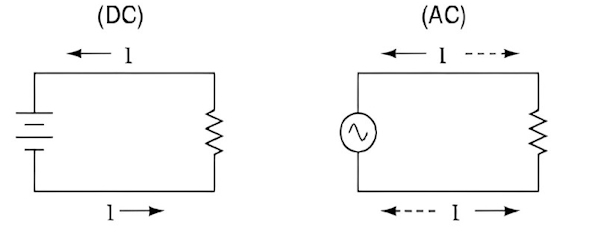
مدار با منبع مستقیم

اگر منبع تغذیه اصلی در مدار مستقیم باشد، به آن مدار مستقیم می‌گویند و برای درک بهتر انواع مدار الکتریکی چیست، چند مثال در این رابطه آورده شده است.

مثال اول برای مدار با منبع جریان مستقیم

در مدار شکل زیر یک منبع تغذیه مستقیم با ولتاژ ۶ ولت داریم که جریان ۲ آمپر از آن عبور می‌کند. مقدار مقاومت را محاسبه کنید.

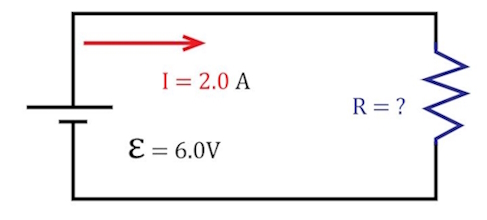
با استفاده از قانون اهم خیلی راحت می‌توانیم مقاومت را محاسبه کنیم.

$$V = I R$$

$$R=\frac{6}{2}=3\Omega$$

مثال دوم برای مدار با منبع جریان مستقیم

در مدار شکل زیر سه مقاومت به صورت متوالی قرار گرفته‌اند، اگر جریان معادل ۲ آمپر از آن‌ها عبور کند، ولتاژ منبع را محاسبه کتید.

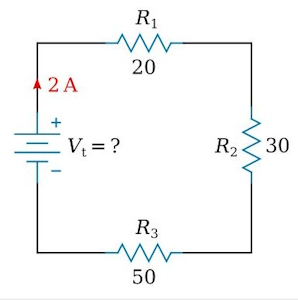
پاسخ:

با استفاده از قانون اهم ولتاژ را برای هر مقاومت به صورت جداگانه محاسبه می‌کنیم و سپس آن‌ها را جمع جبری می‌کنیم .

$$V_1 = I \times R_1 = 40V$$

$$ V_2 = I \times R_2 = 60 \, V $$

$$V_3 = I \times R_3= 100 \, V$$

در نتیجه ولتاژ کل با مقدار زیر برابر است:

$$ V_{total} = V_1 + V_2 + V_3 = 40 \, V + 60 \, V + 100 \, V = \mathbf{200 \, V} $$

مثال سوم برای مدار با منبع جریان مستقیم

در مدار شکل زیر ولتاژ منبع تغذیه برابر ۲۰ ولت و $$R_1 = 100 \; \Omega$$ و $$R_2 = 300 \; \Omega$$ است. جریان و $$V_{R_1}$$ و $$V_{R_2}$$ را محاسبه کنید.

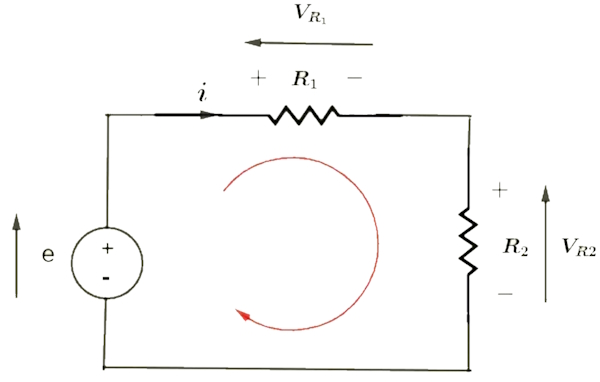
از معادله KVL استفاده می‌کنیم و مطابق شکل حلقه را در جهت ساعتگرد می‌پیماییم.

$$e - V_{R_1} - V_{R_2} = 0$$

و با استفاده از قانون اهم خواهیم داشت:

$$V_{R_1} = i R_1$$

$$V_{R_2} = i R_2$$

این دو معادله را در معادله اول جایگذاری می‌کنیم.

$$e - i R_1 - i R_2 = 0$$

$$i R_1 + i R_2 = e$$

$$i ( R_1 + R_2) = e$$

$$i = \dfrac{e}{R_1 + R_2}$$

$$i = \dfrac{20}{100 + 300} = 0.05$$

اکنون $$V_{R_1}$$ و $$V_{R_2}$$ را محاسبه می‌کنیم.

$$V_{R_1} = i R_1 = 0.05 \times 100 = 5$$

$$V_{R_2} = i R_2 = 0.05 \times 300 = 15$$

۸. طبقه‌بندی مدار براساس اجزا

می‌توانیم مدارها را بر اساس عناصر در مدار نیز طبقه‌بندی کنیم. در زیر فهرستی از انواع مختلف مدارها بر اساس عناصر مدار آن ارائه شده است:

• مدار مقاومتی (فقط حاوی مقاومت‌ها)
• مدار خازنی (فقط حاوی خازن)
• مدار القایی (فقط شامل القاگر)
• مدار RL (مقاومتی – القایی)
• مدار RC (مقاومتی – خازنی)
• مدار LC (القایی – خازنی)
• مدار RLC (مقاومتی – القایی – خازنی)

همان‌طور که در ابتدای این مقاله گفته شد باید توجه داشت که این دسته‌بندی‌ها براساس هدف و نوع کاربرد صورت گرفته است.

نتیجه‌گیری

مدارهای الکترونیکی، سنگ بنای فناوری مدرن است که اجزای الکتریکی به هم پیوسته آن‌ها هستند که دستگاه‌های روزمره ما را تأمین می‌کنند و امکان شگفتی‌های نوآوری را که روزانه با آن مواجه می‌شویم، فراهم می‌کنند. ازجمله تلفن هوشمند، سیستم استریو خانگی و ناوبری روان GPS را می‌توان نام برد، همه آن‌ها به کارکرد پیچیده مدارهای الکترونیکی مدیون هستند. با مطالعه این مقاله در مجله فرادرس با انواع مدار الکتریکی چیست و دسته‌بندی‌های آن آشنا شدید. همچنین برخی اصطلاحات و کاربردهای مخصوص برای هر کدام نیز اشاره شد. در آینده بیشتر درمورد مدارها و قطعات الکترونیکی مقاله منتشر خواهد شد.