الگوریتم DBSCAN چیست؟ – به زبان ساده + نحوه پیاده سازی

تحلیل خوشه‌بندی از جمله روش‌های یادگیری نظارت نشده است که نقاط داده را به چندین گروه یا به اصطلاح «خوشه» (Cluster) تقسیم می‌کند. به این صورت، نقاط داده مشابه در گروه‌های یکسان قرار گرفته و مشخصات نمونه‌های هر گروه با دیگری متفاوت است. به‌طور کلی و با وجود اینکه دامنه الگوریتم‌های خوشه‌بندی گسترده است، اغلب از رویکردهای پایه مانند خوش‌بندی K-Means و «سلسله مراتبی» (Hierarchical) استفاده می‌شود. الگوریتم‌هایی که با وجود کارآمدی بالا، قابلیت‌های اندکی در اختیار شما قرار می‌دهند. از همین جهت، به مرور زمان توسعه الگوریتم‌های پیشرفته‌تری همچون DBSCAN رواج پیدا کرد. در این مطلب از مجله فرادرس می‌خواهیم یاد بگیریم الگوریتم DBSCAN چیست و چگونه پیاده‌سازی می‌شود. الگوریتمی که تقسیم‌بندی داده‌ها را بر اساس فاصله آن‌ها با یک‌دیگر انجام می‌دهد.

در این مطلب ابتدا می‌آموزیم الگوریتم DBSCAN چیست و چرا نیاز داریم از این الگوریتم خوشه‌بندی استفاده کنیم. سپس به بررسی دو مفهوم دسترسی‌پذیری و اتصال می‌پردازیم و از چگونگی فرایند انتخاب پارامتر در الگوریتم DBSCAN می‌گوییم. در انتها این مطلب با نحوه پیاده‌سازی الگوریتم DBSCAN در زبان برنامه‌نویسی پایتون آشنا می‌شویم و عملکرد سه الگوریتم خوشه‌بندی K-Means، «سلسله مراتبی» (Hierarchical) و DBSCAN را با یک‌دیگر مقایسه می‌کنیم.

الگوریتم DBSCAN چیست؟

عبارت DBSCAN مخفف (Density Based Spatial Clustering of Applications with Noise) به معنی خوشه‌بندی فضایی مبتنی‌بر چگالی برای کاربردهایی است که با داده‌های نویزی سر و کار دارند. الگوریتم DBSCAN در سال ۱۹۹۶ و توسط تیم تحقیقاتی «مارتین اِستر» (Martin Ester) معرفی شد. این الگوریتم مبتنی‌بر چگالی است و نواحی متراکم یا همان خوشه‌ها را در فضای ویژگی از نواحی با چگالی کمتر جدا می‌کند. در نتیجه می‌تواند خوشه‌هایی با شکل و اندازه متفاوت را در میان حجم زیادی از داده‌های حاوی نویز و نمونه پرت شناسایی کند.

الگوریتم DBSCAN نسبت به نمونه‌های پرت مقاوم بوده و نیازی به مشخص کردن تعداد خوشه‌ها از قبل نیست. برخلاف تکنیک‌های خوشه‌بندی دیگری مانند K-Means که وظیفه تعیین تعداد «مراکز خوشه» (Centroids) برعهده کاربر است. الگوریتم DBSCAN از دو پارامتر زیر بهره می‌برد:

• پارامتر Epsilon: معیار فاصله‌ای که برای تخمین موقعیت نقاط داده همسایه مورد استفاده قرار می‌گیرد. به بیان دیگر، تعریف پارامتر Epsilon برابر با شعاع دایره شکل گرفته اطراف هر نمونه، برای تعیین میزان تراکم است.
• پارامتر minPoints: حداقل نقاط داده‌ای که یک ناحیه متراکم را تشکیل می‌دهند. تعداد این نمونه‌ها می‌تواند در یک حدآستانه مشخص باشد. نمونه‌هایی که با عنوان «نقاط مرکزی» (Core Points) نیز شناخته می‌شوند.

در ابعاد بالاتر، دایره به «ابرکره» (Hypersphere)، پارامتر Epsilon به شعاع ابرکره و minPoints به حداقل نقاط داده مورد نیاز درون ابرکره تبدیل می‌شود. برای درک بیشتر تصویر زیر را در نظر بگیرید:

در این تصویر نقاط داده با رنگ خاکستری مشخص شده‌اند. الگوریتم DBSCAN دایره‌ای به شعاع «اپسیلون» (Epsilon) اطراف نقاط داده ترسیم و آن‌ها را در یکی از سه گروه مرکزی، «مرزی» (Border Points) و نویز قرار می‌دهد. داده‌ای مرکزی است که دایره اطراف آن حداقل به تعداد پارامتر minPoints نمونه داشته باشد. اگر تعداد نمونه‌های اطراف داده کمتر از پارامتر minPoints باشد مرزی و در صورتی که هیچ نمونه‌ای در شعاع اپسیلون نباشد، نویز نام می‌گیرد.

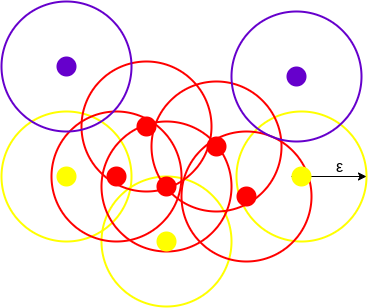
تصویر بالا خوشه‌ای ساخته شده با الگوریتم DBSCAN و minPoints برابر با ۳ را نشان می‌دهد. در اینجا دایره‌ای به شعاع اپسیلون اطراف هر نقطه داده ترسیم شده است. این دو پارامتر به ساخت خوشه‌هایی در فضای بالا کمک می‌کنند.

همه نقاط داده با حداقل ۲ نمونه دیگر در دایره به عنوان نقطه مرکزی شناخته و با رنگ قرمز مشخص شده‌اند. نقاط دیگر با کمتر از ۳ اما بیشتر از ۱ نمونه -شامل همان نمونه- نقاط مرزی در نظر گرفته شده و به رنگ زرد هستند. در آخر نقاط داده‌ای که فاقد هرگونه همسایه‌ای در اطراف خود هستند نقش نویز را داشته و با رنگ بنفش ترسیم شده‌اند. در الگوریتم DBSCAN از فاصله اقلیدسی برای تعیین موقعیت نقاط داده در فضا ویژگی استفاده می‌شود. همچنین برخلاف سایر الگوریتم‌ها، DBSCAN تنها یک مرتبه دیتاست را پایش می‌کند. حالا که فهمیدیم منظور از الگوریتم DBSCAN چیست، در بخش بعدی یاد می‌گیریم که چرا به این رویکرد خاص از خوشه‌بندی نیاز داریم.

چرا به خوشه بندی DBSCAN نیاز است؟

شاید برای شما سوال باشد که با وجود در دسترس بودن الگوریتم‌های پایه خوشه‌بندی، دیگر چرا باید هزینه و زمان صرف یادگیری الگوریتم‌هایی مانند DBSCAN شود. برای پاسخ به این پرسش ابتدا باید شرح دقیقی از نقش خوشه‌بندی ارائه دهیم. خوشه‌بندی یا Clustering نوعی تکنیک یادگیری نظارت نشده است که نقاط داده را بر اساس ویژگی‌های مشخصی به چند گروه مختلف تقسیم می‌کند. در این بین الگوریتم‌های K-Means و «سلسله مراتبی» (Hierarchical) از محبوبیت بالایی برخوردار هستند. برخی از کاربردهای الگوریتم‌های خوشه‌بندی عبارت‌اند از:

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در فرادرس

کلیک کنید

• خوشه‌بندی اسناد
• موتورهای توصیه‌گر
• بخش‌بندی تصویر
• بخش‌بندی بازار
• دسته‌بندی نتایج جستجو
• تشخیص ناهنجاری

همه این کاربردها از مفهوم خوشه‌بندی برای رسیدن به هدف نهایی خود بهره می‌برند. در نتیجه، به‌دست آوردن یک تصویر کلی از خوشه‌بندی بسیار حائز اهمیت است. اما دو الگوریتم K-Means و سلسله مراتبی با دو مشکل عمده روبه‌رو هستند. به این صورت که هیچ‌کدام قادر به تشکیل خوشه‌هایی با شکل و نسبت تراکم متفاوت نیستند. نیاز به الگوریتم DBSCAN از همین موضوع نشات می‌گیرد. برای درک بهتر، مثال زیر را در نظر بگیرید. نقاط داده متراکمی که به شکل دایره‌های متحدالمرکز درآمد‌ه‌اند:

در این تصویر، سه خوشه متراکم مختلف به شکل دایره‌های متحدالمرکز با کمی نویز مشاهده می‌شوند. با اجرا دو الگوریتم خوشه‌بندی K-Means و سلسله مراتبی نتایج زیر به‌دست می‌آید:

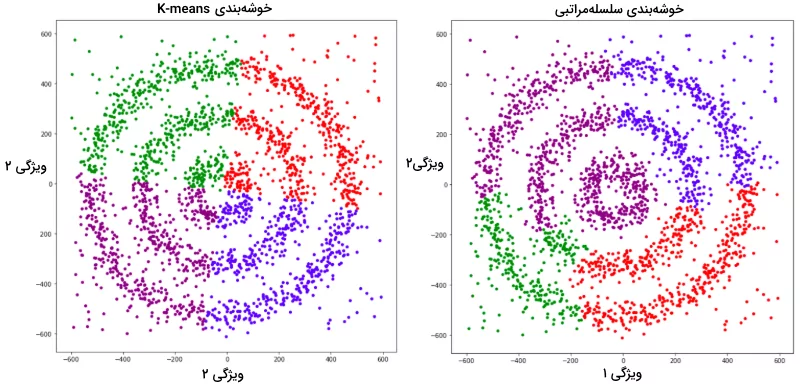
شاید بپرسید که چرا این دو نمودار در چهار رنگ ترسیم شده‌اند. همان‌طور که پیش‌تر نیز توضیح دادیم، این نمودار داده‌های نویزی را هم با رنگ بنفش شامل می‌شود. با توجه به دو نمودار بالا، هیچ‌کدام از دو الگوریتم K-Means و سلسله مراتبی نتوانسته‌اند نمونه‌های نویزی را شناسایی و نقاط داده را به درستی دسته‌بندی کنند. اما در تصویر زیر شاهد نمودار حاصل از اجرا الگوریتم DBSCAN هستید:

بر اساس نتیجه به‌دست آمده، الگوریتم DBSCAN نه تنها نقاط داده را به درستی دسته‌بندی کرده بلکه عملکرد بسیار خوبی در تشخیص نمونه‌های نویزی دیتاست داشته است.

آموزش خوشه بندی با فرادرس

خوشه‌بندی از جمله تکنیک‌های اساسی در یادگیری ماشین و علم داده است که به دسته‌بندی داده‌ها به گروه‌های مشابه یا همان خوشه‌ها می‌پردازد. این روش به ما امکان می‌دهد تا بدون نیاز به برچسب‌های از پیش تعیین شده، ساختارهای پنهان را در داده‌ها کشف کنیم. الگوریتم‌های خوشه‌بندی مانند DBSCAN کاربردهای گسترده‌ای در جهان حقیقی دارند و در مواردی که شکل خوشه‌ها نامنظم است یا داده‌ها دارای نویز هستند، عملکرد بسیار خوبی از خود نشان می‌دهد. برخی از کاربردهای مهم این الگوریتم عبارت‌اند از:

• تشخیص الگوهای ترافیک شهری
• دسته‌بندی مشتری‌ها در بازاریابی
• شناسایی مناطق پرجمعیت
• تحلیل رفتار کاربران در شبکه‌های اجتماعی

برای یادگیری موثر الگوریتم‌های خوشه‌بندی، استفاده از دوره‌های آموزشی بسیار مفید است. این دوره‌ها نه تنها مفاهیم نظری را به خوبی توضیح می‌دهند، بلکه با ارائه مثال‌های عملی شما را برای به‌کارگیری این تکنیک‌ها در پروژه‌های واقعی آماده می‌کنند. در همین راستا، مجموعه فیلم‌های آموزشی فرادرس انتخاب مناسبی برای یادگیری خوشه‌بندی هستند. در فهرست زیر، لینک چند مورد از دوره‌های جامع و کاربردی فرادرس که می‌توانند در این زمینه به شما کمک کنند قرار گرفته است:

• فیلم آموزش کاهش تعداد رنگ تصاویر با استفاده از روش‌های خوشه‌بندی هوشمند فرادرس
• فیلم آموزش خوشه‌بندی با الگوریتم‌های تکاملی و فراابتکاری فرادرس
• فیلم آموزش خوشه‌بندی سلسله مراتبی در آر R فرادرس

بنابراین اگر می‌خواهید در زمینه خوشه‌بندی و الگوریتم‌های پیشرفته‌ای مانند DBSCAN مهارت کسب کنید، مشاهده این فیلم‌های آموزشی را به شما پیشنهاد می‌کنیم.

دسترسی پذیری و اتصال

پس از آنکه یاد گرفتیم الگوریتم DBSCAN چیست و چه کاربردی دارد، در ادامه و برای پیش‌روی بیشتر لازم است تا با دو مفهوم «دسترسی‌پذیری» (Reachability) و «اتصال» (Connectivity) آشنا شویم. قابلیت دسترسی‌پذیری به امکان دسترسی یک نقطه داده به نقطه داده دیگر به‌طور مستقیم یا غیرمستقیم اشاره دارد. این در حالی است که معیار اتصال مشخص می‌کند آیا دو نمونه در یک خوشه مشابه قرار می‌گیرند یا خیر. برحسب معیارهای دسترسی‌پذیری و اتصال، در الگوریتم DBSCAN دو نمونه ممکن است در یکی از سه دسته زیر قرار بگیرند:

• «قابل دسترسی مستقیم» (Directly Density-Reachable)
• «نقطه قابل دسترسی» (Density-Reachable)
• «نقاط متصل» (Density-Connected)

نقطه $$X$$ نسبت به دو پارامتر Epsilon و minPoints برای نقطه $$Y$$ قابل دسترسی مستقیم است اگر:

1. نقطه $$X$$ در همسایگی $$Y$$ قرار بگیرد. به بیان ساده‌تر، فاصله $$X$$ از $$Y$$ کمتر یا مساوی اپسیلون باشد.
2. نقطه $$Y$$ مرکزی باشد.

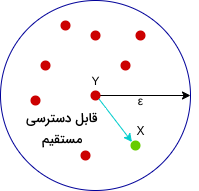
در اینجا نقطه $$X$$ قابل دسترسی مستقیم $$Y$$ است. اما برعکسش صادق نیست. از طرف دیگر، نقطه $$X$$ نسبت به پارامترهای Epsilon و minPoints قابل دسترس $$Y$$ است؛ اگر زنجیره‌ای از نقاط $$P_1$$، $$P_2$$، $$P_3$$، ...، $$P_n$$ وجود داشته و دو معادله  $$P_1 = X$$ و $$P_n = Y$$ به شرط قابلیت دسترسی مستقیم  $$P_i + 1$$ به $$P_i$$ برقرار باشند.

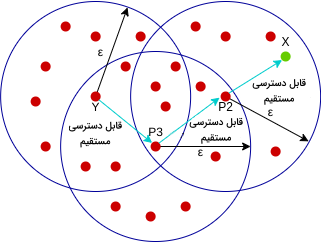
به این شکل $$X$$ قابل دسترس برای $$Y$$، قابل دسترس مستقیم از $$P_2$$، نقطه $$P_2$$ در دسترس مستقیم $$P_3$$ و $$P_3$$ برای $$Y$$ و به‌طور مستقیم قابل دستیابی است. اما جریان برگشتی وجود ندارد.

نقطه $$X$$ به $$Y$$ متصل است اگر نقطه $$O$$ وجود داشته باشد که نسبت به پارامترهای Epsilon و minPoints به $$X$$ و $$Y$$ دسترسی داشته باشد.

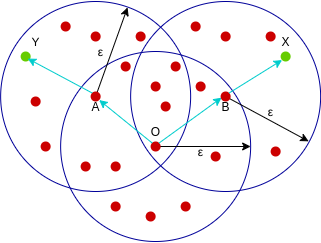
در این مثال هم $$X$$ و هم $$Y$$ از $$O$$ در دسترس بوده و به همین خاطر می‌توانیم بگوییم نقطه $$X$$ به $$Y$$ متصل است. حالا که می‌دانیم الگوریتم DBSCAN چیست و با دو معیار دسترسی‌پذیری و اتصال نیز آشنا شدیم، بخش بعدی را به توضیح نحوه انتخاب پارامتر در این الگوریتم اختصاص می‌دهیم.

انتخاب پارامتر در الگوریتم DBSCAN

الگوریتم DBSCAN حساسیت بالایی نسبت به مقادیر Epsilon و minPoints دارد. از همین جهت بسیار مهم است که از نحوه انتخاب این پارامترها مطلع شویم. چرا که حتی تغییری کوچک در این مقادیر ممکن است نتایج الگوریتم DBSCAN را به کل متحول کند. مطابق با عبارت زیر، مقدار پارامتر minPoints باید حداقل یکی بیشتر از ابعاد دیتاست باشد:

$$minPoints \ge Dimensions + 1$$

نمی‌توان مقداری برابر با ۱ برای minPoints در نظر گرفت. زیرا هر خوشه تنها شامل یک نمونه خواهد بود. به همین خاطر، مقدار minPoints باید حداقل ۳ باشد. اغلب مقدار minPoints را دو برابر ابعاد دیتاست قرار می‌دهند اما همچنان به نوع مسئله نیز بستگی دارد.

مقدار متغیر Epsilon را می‌توان از نمودار «K فاصله» (K-distance) به‌دست آورد. در واقع بیشینه انحنا یا همان «آرنج» (Elbow) نمودار بیانگر مقدار Epsilon است. هرچه مقدار انتخابی برای این پارامتر کوچکتر باشد، تعداد خوشه‌ها افزایش یافته و نقاط داده بیشتری به عنوان نویز شناسایی می‌شوند. از سوی دیگر با انتخاب مقداری بسیار بزرگ برای Epsilon، خوشه‌های کوچک در یک خوشه بزرگ ادغام شده و جزییات زیادی از بین می‌رود. در مطلب دیگری از مجله فرادرس، به‌طور مفصل درباره آمار پارامتری و ناپارامتری توضیح داده‌ایم که می‌توانید آن را از طریق لینک زیر مطالعه کنید:

پیاده سازی الگوریتم DBSCAN در پایتون

پس از  پاسخ دادن به پرسش الگوریتم DBSCAN چیست و شناخت فرایند انتخاب پارامتر، در این بخش به شرح قدم به قدم مراحل پیاده‌سازی این الگوریتم در زبان برنامه‌نویسی پایتون می‌پردازیم. برای آشنایی بیشتر با جنبه کاربردی الگوریتم‌های یادگیری ماشین، می‌توانید فیلم آموزش رایگان یادگیری ماشین با پایتون فرادرس را از لینک زیر مشاهده کنید:

فیلم آموزش رایگان یادگیری ماشین با پایتون – سریع و آسان در ۱۸۰ دقیقه + گواهینامه در فرادرس

کلیک کنید

مرحله ۱

در قدم اول، کتابخانه‌های مورد نیاز را مانند زیر بارگذاری می‌کنیم:

مرحله ۲

سپس و برای تسهیل در مصورسازی، دیتاستی با دو ویژگی ایجاد می‌کنیم. این کار را با تعریف تابعی به نام PointsInCircumانجام می‌دهیم. تابع PointsInCircumدو پارامتر ورودی rو nرا به عنوان شعاع و تعداد نقاط داده دریافت کرده و آرایه‌ای متشکل از نقاط داده جدید به شکل دایره را برمی‌گرداند. پیاده‌سازی این فرایند با کمک دو منحنی سینوس و کسیونس انجام می‌شود:

مرحله ۳

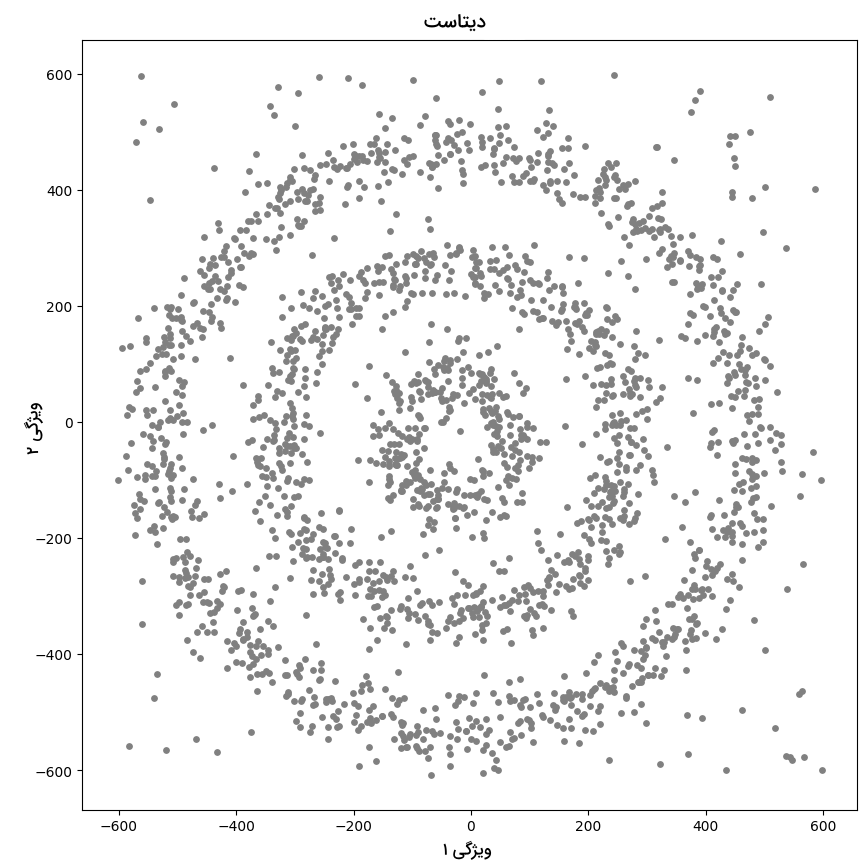
با این حال، یک دایره برای درک توانایی خوشه‌بندی الگوریتم DBSCAN کافی نیست. از همین رو، سه دایره متحدالمرکز با شعاع متفاوت تعریف می‌کنیم. علاوه‌بر آن، برای مقایسه عملکرد الگوریتم‌های مختلف، به دیتاست نویز اضافه شده است:

دیتاست نهایی مانند زیر خواهد بود:

مرحله ۴

در انتها می‌خواهیم نقاط داده را در فضای ویژگی ترسیم کنیم. در قطعه کد زیر از نمودار نقطه‌ای برای نمایش نقاط داده استفاده شده است:

خروجی به شکل زیر است:

حالا و پس از ایجاد دیتاست مورد نیاز برای عمل خوشه‌بندی، در بخش بعدی نتایج سه الگوریتم K-Means، سلسله مراتبی و DBSCAN را با هم مقایسه می‌کنیم.

مقایسه الگوریتم های K-Means و سلسله مراتبی و DBSCAN

هر سه الگوریتم K-Means، سلسله مراتبی و DBSCAN از جمله راهکارهای رایج خوشه‌بندی به حساب می‌آیند که در مسائل متنوعی به‌کار گرفته می‌شوند. تا اینجا یاد گرفتیم الگوریتم DBSCAN چیست و چگونه پیاده‌سازی می‌شود. حالا و در ادامه، عملکرد این سه الگوریتم خوشه‌بندی را نسبت به دیتاست ایجاد شده در بخش قبل با یک‌دیگر مقایسه می‌کنیم.

الگوریتم K-Means

برای پیاده‌سازی الگوریتم K-Means، ابتدا کلاس KMeansرا از کتابخانه Scikit-learn بارگذاری کرده و پس از ساخت نمونه‌ای جدید، متد fitرا به‌منظور برازش فراخوانی می‌کنیم:

در مرحله بعد و برای مدیریت راحت‌تر داده، برچسب‌های الگوریتم را در ستون جدیدی به نام KMeans_labels ذخیره و نتیجه را به نمایش می‌گذاریم:

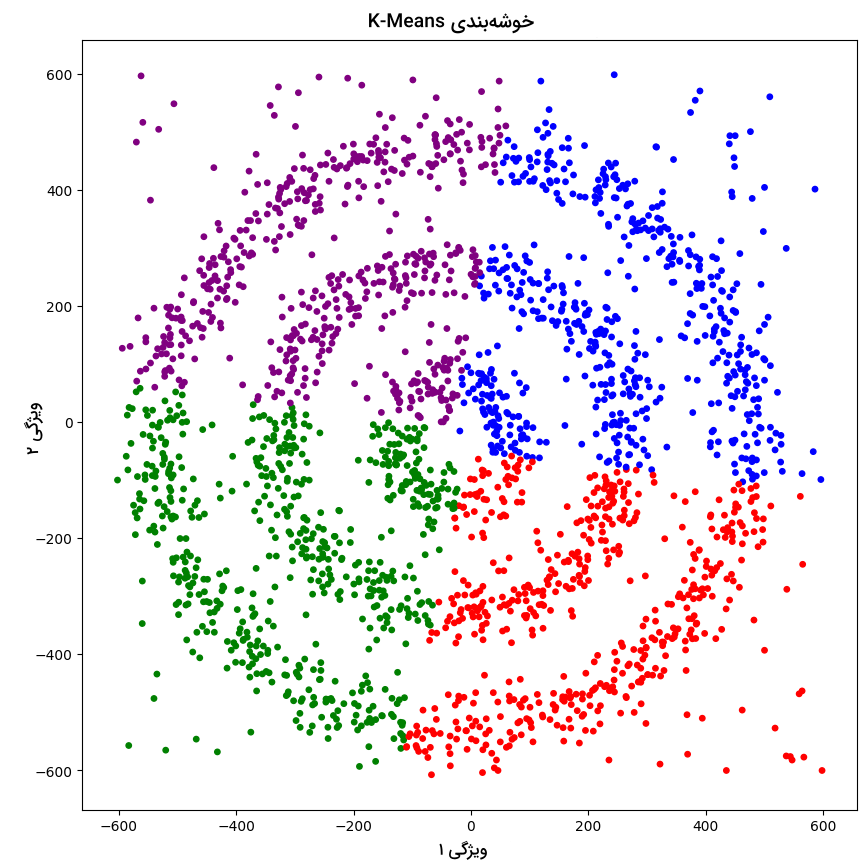
در تصویر زیر، نمودار نقطه‌ای حاصل از اجرا الگوریتم K-Means را مشاهده می‌کنید:

همان‌طور که ملاحظه می‌کنید، الگوریتم K-Means نتوانسته نقاط داده را در چهار خوشه مختلف دسته‌بندی کند. همچنین تشخیص داده‌های نویزی هم به‌درستی انجام نشده است.

الگوریتم سلسله مراتبی

برای اجرا الگوریتم سلسله مراتبی از نوع «تجمیعی» (Agglomerative) خوشه‌بندی بهره می‌بریم. نوع دیگر الگوریتم‌های خوشه‌بندی «تقسیمی» (Divisive) نام دارند. نحوه پیاده‌سازی الگوریتم سلسله مراتبی به شرح زیر است:

در ادامه و پس از استخراج برچسب‌های مدل تجمیعی، نتیجه را به نمایش می‌گذاریم:

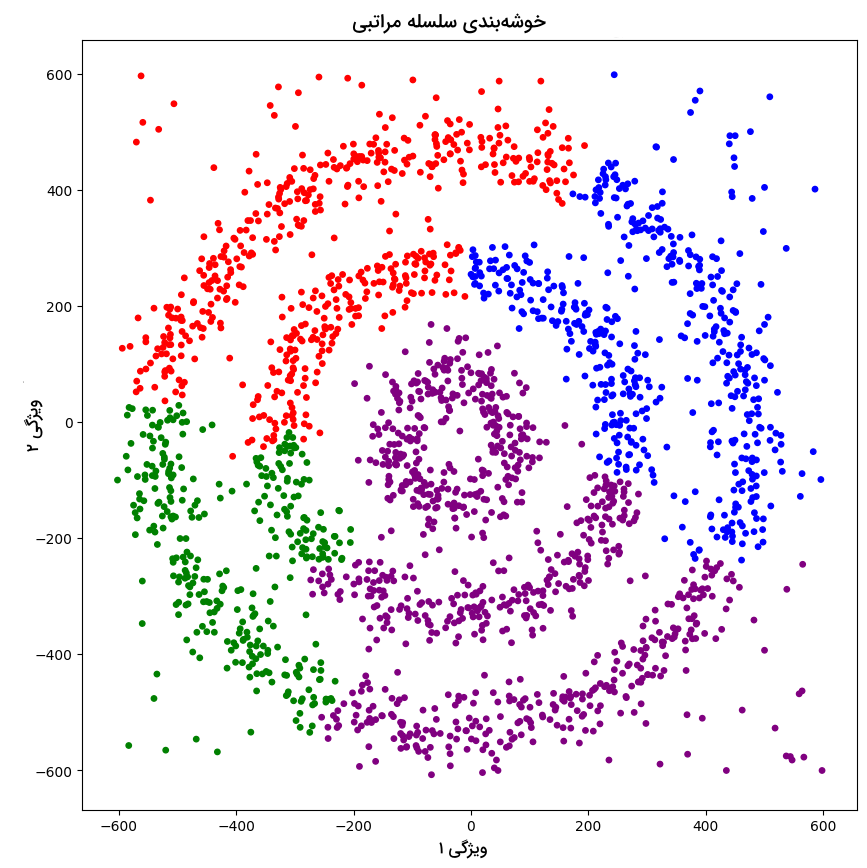
نمودار نقطه‌ای حاصل از اجرا قطعه کد بالا مانند زیر است:

با بررسی نمودار فوق متوجه می‌شویم که الگوریتم سلسله مراتبی نیز قادر به دسته‌بندی مناسب داده‌ها نبوده است.

الگوریتم DBSCAN

در قدم اول و برای پیاده‌سازی الگوریتم DBSCAN در پایتون، لازم است تا کلاس DBSCANرا از ماژول clusterکتابخانه Scikit-learn فراخوانی کنیم. سپس می‌خواهیم کلاس DBSCANرا بدون هیچ پارامتر بهینه‌سازی اجرا و به بررسی نتایج به‌دست آمده بپردازیم:

مقدار پیش‌فرض Epsilon برابر با ۰/۵ و minPoints مساوی ۵ است. با اجرای قطعه کد زیر، نمودار نقطه‌ای حاصل از اجرا الگوریتم DBSCAN ترسیم می‌شود:

خروجی مانند زیر است:

همان‌طور که ملاحظه می‌کنید، همه نقاط داده به رنگ بنفش هستند. به این معنی که الگوریتم همه نمونه‌ها را نویز در نظر گرفته است. دلیل این اتفاق مقدار بسیار پایین Epsilon و پارامترهایی است که بهینه نشده‌اند. در نتیجه باید مقدار بهینه Epsilon و minPoints را پیدا کرده و مجدد مدل را آموزش دهیم.

برای محاسبه مقدار Epsilon از نمودار K-distance کمک می‌گیریم. رسم این نمودار نیازمند فاصله میان تمام نقاط داده و نزدیک‌ترین همسایه به آن‌ها است. اطلاعاتی که با بهره‌گیری از کلاس NearestNeighborsو ماژول neighborsحاصل می‌شود:

متغیر distancesآرایه‌ای متشکل از فاصله میان تمام نقاط داده موجود در دیتاست با نزدیک‌ترین همسایه آن‌ها است. محتوا این آرایه عبارت است از:

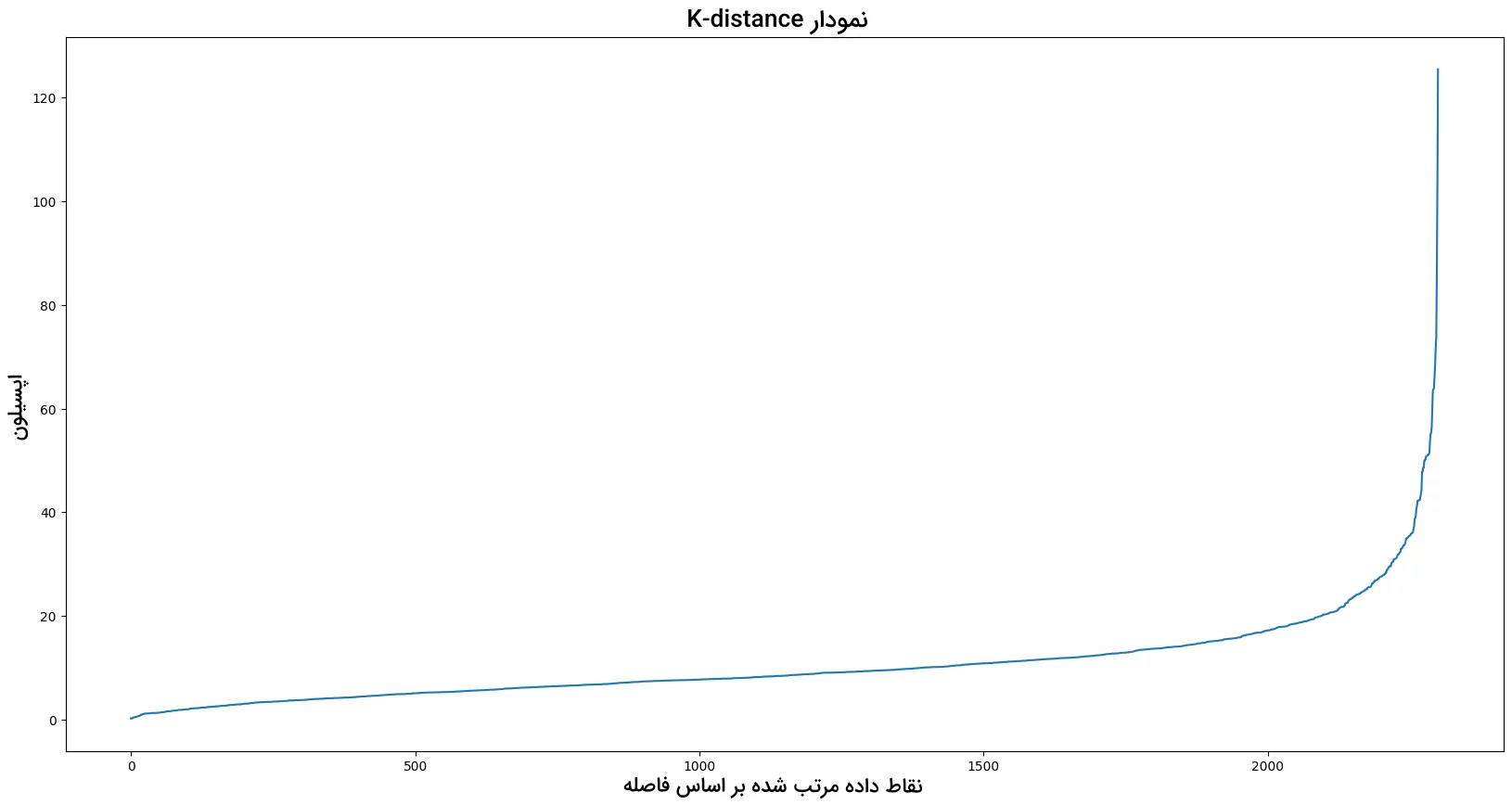
با استفاده از قطعه کد زیر نمودار K-distance را رسم و مقدار Epsilon به‌دست می‌آید:

نمودار K-distance به شکل زیر است:

مقدار بهینه Epsilon در بیشینه انحنا نمودار K-distance قرار داشته و در اینجا برابر با ۳۰ است. در قدم بعد باید مقدار minPoints را پیدا کنیم. پارامتری که مقدار آن به نوع مسئله بستگی دارد. برای مثال، مقدار minPoints را برابر با ۶ قرار می‌دهیم:

سپس برچسب‌های حاصل از الگوریتم DBSCAN را به ویژگی جدیدی در دیتاست نسبت داده و تعداد هر کدام را در خروجی چاپ می‌کنیم:

در تصویر زیر تعداد تکرار برچسب‌های دیتاست را مشاهده می‌کنید:

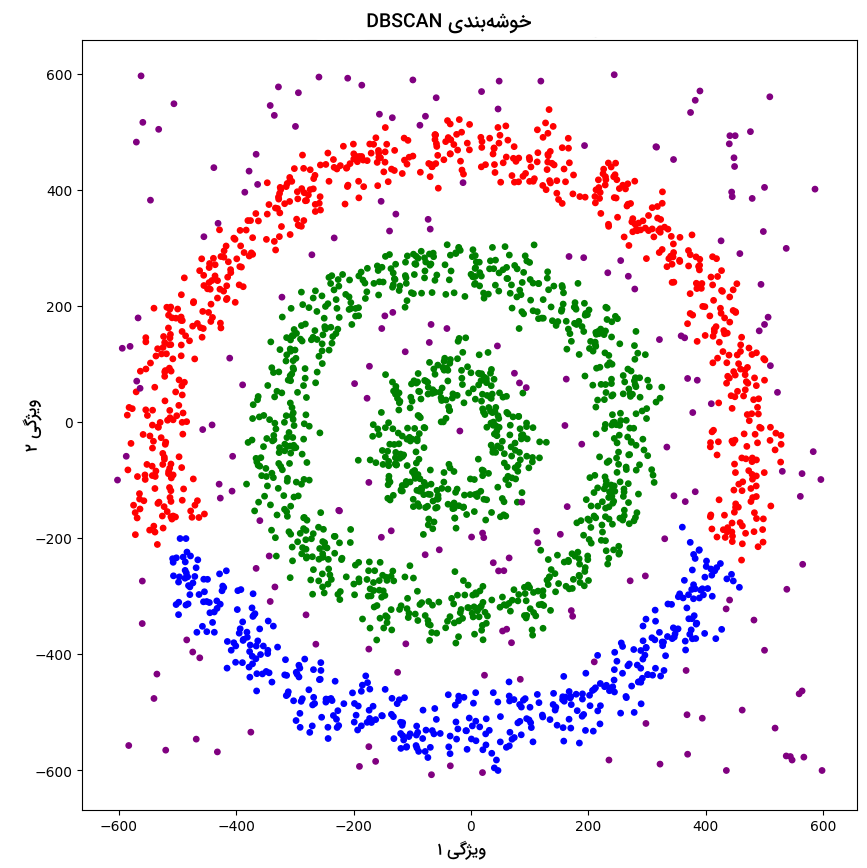
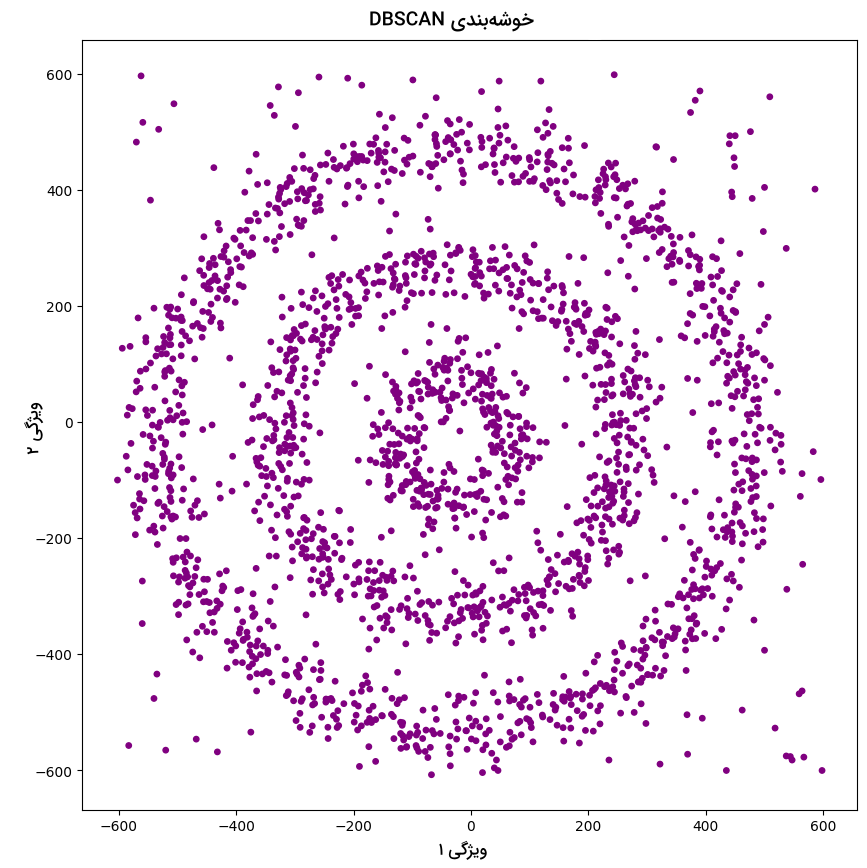
الگوریتم DBSCAN به‌خوبی نمونه‌های نویزی را از سایر دیتاست جدا می‌کند. در این مثال ۰، ۱ و ۲ سه خوشه مختلف و ۱- نویز است. هدف از اجرا قطعه کد زیر، ترسیم نتایج الگوریتم DBSCAN است:

نمودار نقطه‌ای حاصل به شرح زیر است:

همان‌طور که مشاهده می‌کنید، نقاط داده در سه خوشه مختلف جای گرفته و نویزها شناسایی و با رنگ بنفش به نمایش گذاشته شده‌اند. باید توجه داشته باشید که اگرچه الگوریتم DBSCAN خوشه‌ها را مبتنی‌بر تنوع چگالی ایجاد می‌کند، همچنان در تشخیص خوشه‌هایی با چگالی مشابه با چالش روبه‌رو است. از طرف دیگر، همزمان با افزایش ابعاد داده، وظیفه ساخت خوشه‌ها نیز برای DBSCAN دشوار شده و با مشکل «طلسم ابعاد» (Curse of Dimensionality) مواجه می‌شویم.

در این مطلب یاد گرفتیم الگوریتم DBSCAN چیست و این قبیل از الگوریتم‌های خوشه‌بندی بخشی جدایی‌ناپذیر از جهان گسترده یادگیری ماشین هستند. این حوزه که امروزه در صنایع مختلف کاربردهای فراوانی پیدا کرده، از ابزارهای قدرتمندی مانند زبان برنامه‌نویسی پایتون بهره می‌برد. پایتون با کتابخانه‌های متنوع و قابلیت‌های فراوان، به عنوان یکی از محبوب‌ترین زبان‌ها برای پیاده‌سازی الگوریتم‌های یادگیری ماشین شناخته می‌شود. برای ورود به این دنیای هیجان‌انگیز و کسب مهارت‌های عملی در زمینه خوشه‌بندی و سایر تکنیک‌های یادگیری ماشین، استفاده از منابع آموزشی معتبر بسیار اهمیت دارد.

در همین راستا، فیلم‌های آموزشی فرادرس که توسط اساتید خبره و با تجربه تهیه شده‌اند راهنمای ارزشمندی در مسیر یادگیری هستند. برای مشاهده این دوره‌های آموزشی روی لینک‌های زیر کلیک کنید:

• فیلم آموزش یادگیری ماشین و پیاده‌سازی در پایتون فرادرس – بخش یکم
• فیلم آموزش یادگیری ماشین و پیاده‌سازی در پایتون فرادرس – بخش دوم
• فیلم آموزش یادگیری ماشین با پایتون فرادرس

جمع‌بندی

الگوریتم DBSCAN ابزاری کارآمد برای متخصصان علم داده است که هنگام کار با دیتاست‌های پیچیده و نویزی با تعداد نامشخص خوشه بسیار موثر واقع می‌شود. با این حال مانند هر الگوریتم دیگری، DBSCAN نیز تنها برای نوع خاصی از مسائل کاربرد دارد. به‌دست آوردن درک کافی از داده‌ها، آشنایی با نقاط ضعف و قوت الگوریتم‌های مختلف و انتخاب ابزار مناسب همه از جمله موارد تاثیرگذار در موفقیت فرایند خوشه‌بندی است. در این مطلب از مجله فرادرس یاد گرفتیم الگوریتم DBSCAN چیست و چگونه با استفاده از زبان برنامه‌نویسی پایتون پیاده‌سازی می‌شود. تکنیک مهمی که بهره‌گیری از آن ما را با ساختار داده آشنا می‌سازد.