ارزیابی و رفع خطاهای الگوریتم های داده کاوی — راهنمای مقدماتی

در این نوشته به معرفی مراحلی می‌پردازیم که در زمان عدم کارکرد صحیح الگوریتم های داده کاوی و پیش از اقدام به دیباگ کردن کد باید اجرا کنید. تصور کنید یک روز عالی است و مشغول کدنویسی الگوریتمی هستید که فکر می‌کنید نتایج صحیحی در اختیار شما قرار می‌دهد؛ اما در این موقعیت متوجه می‌شوید که در پیش‌بینی‌های خود اشتباهی داشته‌اید و نتایج مورد نظر خود را دریافت نمی‌کنید.

باید بدانید که در چنین موقعیت‌هایی، همواره پیش از آن که شروع به جستجوی کدهای خود بکنید، مواردی هستند که باید مورد بررسی قرار دهید.

در ادامه و پیش از بخش اصلی مقاله برخی اصطلاح‌ها هستند که باید با آن‌ها آشنا باشید:

1. مجموعه آموزشی (Training Set): به ورودی الگوریتم که برای آموزش دادن و یافتن بهترین برازش برای داده‌ها استفاده می‌شود می‌گوییم.
2. مجموعه اعتبار سنجی متقابل (Cross Validation Set) یا CV: مجموعه داده‌هایی است که با استفاده از آن خطا را در مدل خود که با استفاده از مثال‌های آموزشی آموزش داده‌ایم، تشخیص می‌دهیم.
3. مجموعه تست (Test Set): مجموعه‌ای است که با استفاده از آن مدل خود را تست می‌کنیم و دقتش را تشخیص می‌دهیم.

به طور کلی اگر یک مجموعه آموزشی به شما داده شده باشد، می‌توانید این مجموعه را به 3 بخش فوق‌الذکر با نسبت 60% برای یادگیری، 20% برای اعتبارسنجی و 20% برای تست افراز کنید. البته این فقط یک روش پیشنهادی است و می‌توانید از این روش یا روش‌های دیگر برای تقسیم مجموعه داده‌های خود استفاده کنید.

اینک بسته به این که چه مجموعه داده‌ای را انتخاب کرده باشید، چه ویژگی‌هایی برای ورودی خود در نظر گرفته باشید، پارامتر منظم‌سازی شما چه باشد و بسیاری از موارد دیگر، با یکی از موقعیت‌های زیر مواجه خواهید بود:

1. بایاس بالا (Underfit): اگر فرضیه شما بر اساس مجموعه تست، همخوانی نداشته باشد و همچنین نتوانید فرضیه خود را روی مثال‌های جدید تعمیم بدهید، مشخص می‌شود که فرضیه شما بایاس بالایی دارد یا اصطلاحاً دچار کم‌برازش (underfitting) است.
2. واریانس بالا (Overfit): اگر فرضیه‌های شما روی مجموعه تست عملکرد خوبی دارند؛ اما برای مجموعه اعتبارسنجی یا هر مثال دیگر به درستی عمل نمی‌کنند، فرضیه شما از واریانس بالا یا بیش‌برازش رنج می‌برد.

یک تعادل مناسب بین بایاس-واریانس برای رگرسیون خطی (برای مثال تصور کنید مشغول تخمین قیمت خانه برحسب یک ویژگی مانند اندازه خانه هستیم) در شکل زیر نمایش یافته است. این نمودار با تنها یک ویژگی X (مثال آموزشی) در راستای محور x ترسیم شده است و خروجی (مثال آموزشی) آن در راستای محور Y است. شکل (a) میزان برازش فرضیه روی مجموعه آموزشی را نشان می‌دهد؛ اما به دلیل مقدار بالای زاویه‌دار بودن (angularity) نمی‌توان آن را روی مثال‌های جدید تعمیم داد. شکل (c) نشان می‌دهد که این فرضیه روی مجموعه داده‌های آموزشی برازش ندارد و از این رو نمی‌توان آن را تعمیم داد. شکل (b) برازش بهینه را نشان می‌دهد که برای داده‌های آموزشی و همچنین مجموعه اعتبارسنجی به دست آمده است و همچنین مجموعه اعتبارسنجی به تدریج با افزایش اندازه خانه رشد می‌یابد.

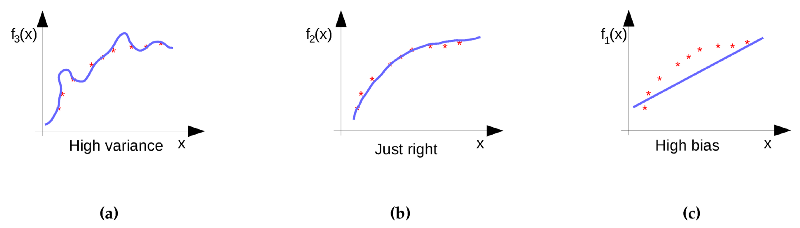
اگر مسئله بالا را درک کرده‌اید، اینک نوبت آن رسیده است که به بررسی آن و یافتن روش حل کردنش بپردازیم.

چگونه واریانس بالا را رفع کنیم؟

واریانس بالا را می‌توان با استفاده از منظم‌سازی (regularization) یا از طریق افزایش تعداد مثال‌های آموزشی حل کرد. منظم‌سازی تضمین می‌کند که پارامترهای فرضیه (تتا برای بهترین برازش) آن قدر پایین است که می‌توان از زاویه‌دار بودن نمودار اجتناب کرد و فرضیه‌ای با تعمیم‌پذیری مناسب به دست آورد.

فیلم آموزش داده کاوی و زبان برنامه نویسی R (رایگان) در فرادرس

کلیک کنید

شکل زیر تابع هزینه را برای قیمت خانه در برابر اندازه خانه به همراه استفاده عملی از منظم‌سازی نشان می‌دهد. منحنی به رنگ آبی بیش‌برازش فرضیه را نشان می‌دهد که برای مجموعه آموزشی به خوبی عمل می‌کند؛ اما امکان تعمیم آن وجود ندارد. در سوی دیگر منحنی رنگ صورتی منظم‌سازی را در عمل نشان می‌دهد. این منحنی برای هر دو مجموعه آموزشی و همچنین مثال‌های جدید به خوبی عمل می‌کند.

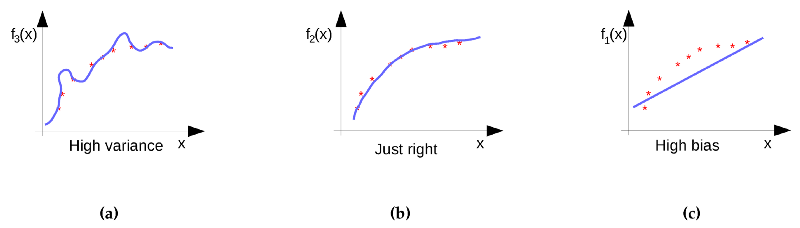
اگر تعداد مثال‌های آموزشی را افزایش دهید، منحنی دیگر نمی‌تواند گوشه‌های زاویه‌دار پیدا بکند و در نتیجه تعمیم به خوبی صورت گرفته است.

چگونه بایاس بالا را رفع کنیم؟

بایاس بالا را می‌توان از طریق افزایش تعداد ویژگی‌ها برای مثال‌های آموزشی مانند افزودن ویژگی‌های چندجمله‌ای به اندازه خانه یا افزایش تعداد ویژگی‌ها مانند موقعیت خانه، تعداد اتاق‌خواب، آشپزخانه، سالن و موارد دیگر رفع کرد. این وضعیت از تبدیل شدن منحنی به یک خط راست جلوگیری می‌کند و بدین ترتیب برای مجموعه‌های آموزشی و مثال‌های جدید به خوبی عمل می‌کند.

نکات مهم

• افزایش تعداد مجموعه‌های آموزشی در صورت وجود بایاس بالا کمک چندانی نمی‌کند.
• باید از بالا گرفتن پارامتر منظم‌سازی (لامبدا) اجتناب کنید، زیرا موجب خطای بالا در پارامترهای تتا می‌شود و نتیجه نهایی به صورت underfitting خواهد بود.
• اگر کنجکاو هستید که چگونه می‌توانیم این مفاهیم را در کد خود پیاده‌سازی کنیم، باید در عمل با «منحنی‌های یادگیری» (Learning Curves) آشنا شوید.

منحنی‌های یادگیری

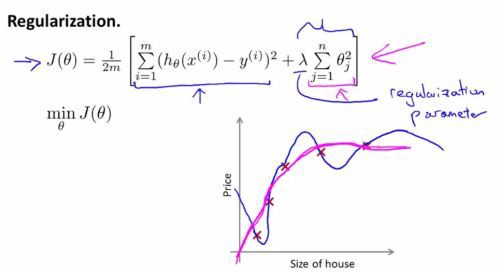
برای درک منحنی‌های یادگیری ابتدا باید نگاهی به منحنی معمول بایاس بالا بیندازیم و آن را بررسی کنیم.

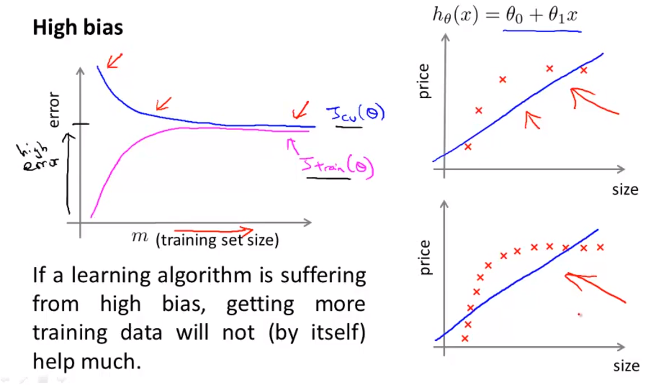
شکل فوق یک منحنی یادگیری با بایاس بالا را برای یک رگرسیون خطی که تنها یک ویژگی دارد نمایش می‌دهد. منحنی‌های یادگیری به همراه خطا (در مجموعه‌های آموزشی و اعتبارسنجی متقابل) در راستای محور y و m (تعداد مثال‌های آموزشی) در راستای محور x رسم شده‌اند. از روی شکل مشخص است که اگر m بسیار کوچک باشد، خطای آموزش بسیار پایین است؛ اما خطای اعتبارسنجی (CV) بسیار بالا است، زیرا مجموعه داده خود را برای تعمیم به مقدار کافی آموزش نداده‌ایم. زمانی که مقدار m را افزایش می‌دهیم، خطای آموزش نیز افزایش می‌یابد، زیرا دیگر نمی‌توان برازش مستقیمی روی مجموعه داده بزرگی داشت؛ اما خطای اعتبارسنجی کاهش می‌یابد، زیرا بهتر از قبل می‌توانیم آن را تعمیم دهیم (چون بهتر آموزش دیده است). با افزایش بیشتر m، خطا برای هر دو مجموعه آموزشی و اعتبارسنجی اشباع می‌شود، زیرا دیگر نمی‌توان برازش را روی مجموعه داده‌های زیاد حفظ کرد و مهم نیست که چه مقدار مجموعه داده در ورودی ارائه می‌شود.

کدنویسی این مفاهیم

در ادامه کد نوشته شده برای مفاهیم فوق را ارائه کرده‌ایم. این کد در محیط Matlab/Octave نوشته شده است؛ اما با توجه به این که می‌خواهیم این مفهوم را درک کنیم، مشکلی وجود نخواهد داشت.

1function [error_train, error_val] = ...
2    learningCurve(X, y, Xval, yval, lambda)
3    
4   m = size(X, 1);
5
6for i = 1:m
7    Xt = X(1:i, :);
8    yt = y(1:i);
9    theta = trainLinearReg(Xt,yt,lambda);
10    error_train(i) = linearRegCostFunction(Xt, yt, theta, 0);
11    error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
12
13%Xval and yval are the cross validation matrix    
14end

ما یک حلقه را از 1 تا تعداد مثال‌های آموزشی (m) اجرا می‌کنیم. X ماتریس اصلی ما است که شامل همه مثال‌ها است. Xt شامل i عدد مثال آموزشی و Yt شامل خروجی متناظر آن‌ها است که در این مثال قیمت خانه‌ها است. در این حالت Xt، Yt و یک پارامتر منظم‌سازی (لامبدا) را به تابع trainLinearReg ارسال می‌کنیم که برازش بهینه (مقادیر تتا) برای تعداد مفروضی از مثال‌های آموزشی و ذخیره‌سازی در تتا بازگشت می‌دهد. در نهایت ماتریس خطا را برای i عدد از مثال‌های آموزشی محاسبه می‌کنیم. (error_train(i شامل خطایی در مجموعه آموزشی برای i عدد مثال‌های آموزشی است. (error_val(i شامل خطایی در مجموعه اعتبارسنجی برای i-اُمین تکرار است. ممکن است متوجه شده باشید که ما کل مجموعه اعتبارسنجی را در هر تکرار ارسال می‌کنیم و این حالت عکس مجموعه آموزشی است. برای محاسبه خطا برای مجموعه آموزشی یا مجموعه اعتبارسنجی می‌توانیم از تابع هزینه استفاده کرده و مقدار صفر را به تابع linearRegCostFunction ارسال کنیم.

1function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
2m = length(y); % number of training example
3h = X*theta;
4sqrError = (h - y).^2;
5J  = (1/(2*m))*sum(sqrError) + (lambda/(2*m))*sum(theta(2:end).^2);
6grad = (1/m).*(X'*(h - y)) + (lambda/m).*theta;
7grad(1) = (1/m)*(sum(h - y));grad = grad(:);
8
9end

زمانی که هر دو ماتریس خطا (آموزشی و اعتبارسنجی) را به دست آوردیم، می‌توانیم آن‌ها را برای بصری‌سازی رسم کنیم.

1[error_train, error_val] = ...
2    learningCurve([ones(m, 1) X], y, ...
3                  [ones(size(Xval, 1), 1) Xval], yval, ...
4                  lambda);
5
6plot(1:m, error_train, 1:m, error_val);
7title('Learning curve for linear regression')
8legend('Train', 'Cross Validation')
9xlabel('Number of training examples')
10ylabel('Error')
11axis([0 13 0 150])

تابع رسم مقادیر خود را از 1 تا m و plots error_train و error_val را برای تعداد متناظری از مثال‌های آموزشی دریافت می‌کند. پس از پیاده‌سازی این وضعیت می‌توانید منحنی مشابه منحنی نمایش یافته در نمودار بایاس بالای فوق به دست آورید.

در مورد وضعیت واریانس بالا نیز می‌توانیم منحنی مشابه شکل زیر به دست آوریم:

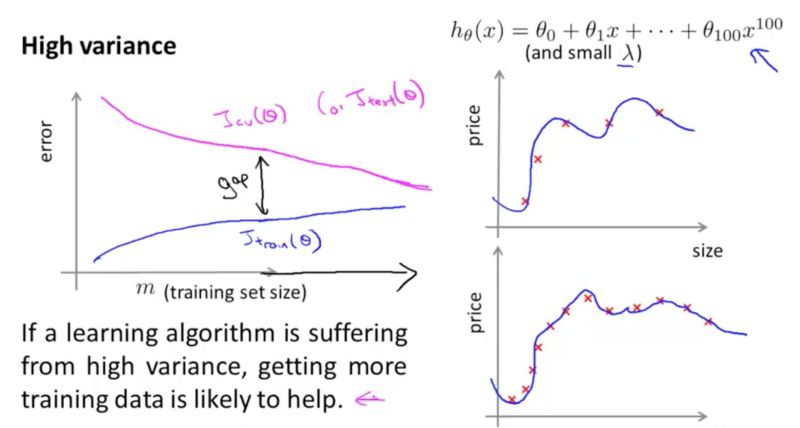
نکات

1. برخلاف حالت بایاس بالا، شکافی بین خطای اعتبارسنجی و خطای آموزشی وجود دارد.
2. افزایش تعداد مثال‌های آموزشی یا پارامتر منظم‌سازی می‌تواند به جلوگیری از واریانس بالا کمک کند.

تا به اینجا، در وضعیتی هستیم که بتوانیم تشخیص دهیم یک نمودار، دارای بایاس بالا یا واریانس بالا است و این نقطه آغاز دیباگ کردن کد الگوریتم است.

تنظیم پارامتر منظم‌سازی (لامبدا)

آخرین نکته‌ای که باید بیان کنیم در مورد پارامتر منظم‌سازی لامبدا است. به طور خاص یک مدل بدون منظم‌سازی (λ = 0) به خوبی با مجموعه آموزشی، برازش می‌یابد؛ اما تعمیم پیدا نمی‌کند. به طور عکس یک مدل با منظم‌سازی بالا روی مجموعه آموزشی و همچنین تست برازش ندارد. انتخاب مناسب λ می‌تواند برازش مناسبی روی داده‌ها به دست دهد. در صورتی که مطالب این نوشته را به دقت پیگیری کرده باشید، اینک می‌توانید به راحتی مقدار بهینه لامبدا را برای مدل خود پیدا کنید. ما باید همان کاری را که در مورد منحنی‌های بهینه انجام می‌دهیم به اجرا درآوریم، یعنی باید یک گراف بین خطا و تعداد مثال‌های آموزشی رسم کنیم. با این وجود این بار پارامتر لامبدا را تغییر می‌دهیم تا خطای متناظر را در مجموعه‌های آموزشی و اعتبارسنجی تشخیص دهیم. ناحیه‌ای که هر دو خطا یعنی خطاهای آموزشی و اعتبارسنجی پایین هستند، مقدار بهینه را برای لامبدا به دست می‌دهد. کد این مفهوم به صورت زیر است:

1for i = 1:length(lambda_vec)
2  lambda  = lambda_vec(i);
3  theta = trainLinearReg(X,y,lambda);
4
5% here X and y are the whole trainig set matrix
6  error_train(i) = linearRegCostFunction(X, y, theta, 0);
7  error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
8  end

بردار lambda_vec برداری است که شامل مقادیر مختلف لامبدا است و قصد داریم از آن استفاده کرده و با تعریف حلقه‌ای روی آن، خطاهای متناظر در مجموعه‌های آموزشی و اعتبارسنجی را پیدا کنیم. در ادامه گراف این مفهوم را می‌بینیم و تلاش خواهیم کرد طرز کار آن را درک کنیم.

از روی گراف مشخص است که انتخاب مقدار لامبدا پیرامون 100 می‌تواند انتخاب مناسبی برای مدل آموزشی باشد، زیرا در این مقطع هر دو مجموعه آموزشی و اعتبارسنجی کمترین مقدار خطا را دارند. در این مقطع، تعدادی از خطاهای ممکن را می‌بینیم که باعث می‌شوند الگوریتم ما عملکرد ضعیفی داشته باشد و همچنین احتمالاً باعث بروز مشکلات الگوریتم ما می‌شوند.

سخن پایانی

بدین ترتیب در این مقاله دیدیم که منحنی یادگیری به رفع حالت‌های بایاس بالا و واریانس بالا کمک می‌کند و همچنین پارامتر منظم‌سازی در مدل می‌تواند صرفه‌جویی زیادی در زمان محاسبات ما ایجاد کند. اگر می‌خواهید کد کامل پیاده‌سازی مفاهیم ارائه شده در این راهنما را ببینید می‌توانید به این آدرس مراجعه کنید.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های برنامه‌‌نویسی
• مجموعه آموزش های تئوری و عملی الگوریتم ژنتیک
• آموزش روش حریصانه در طراحی الگوریتم
• آموزش حل مسائل گسسته با استفاده از الگوریتم PSO
• روش انتخاب الگوریتم داده کاوی — راهنمای کاربردی

==