پیاده سازی اندیکاتور شاخص قدرت نسبی RSI در پایتون — راهنمای گام به گام
اندیکاتور شاخص قدرت نسبی (Relative Strength Index) که بهصورت کوتاه با نام RSI شناخته میشود، یکی از اولین اندیکاتورهایی است که در تحلیل تکنیکال با آن آشنا میشویم و در عین فراگیری، قدرت خوبی نیز در زمینههای مختلفی از خود نشان میدهد. برای آشنایی بیشتر با این اندیکاتور میتوانید به مطلب «آموزش اندیکاتور RSI – نحوه استفاده به زبان ساده» مراجعه کنید. در ادامه، به بررسی پیادهسازی اندیکاتور RSI در پایتون میپردازیم.
آشنایی با اندیکاتور RSI
اندیکاتور RSI، بهنوعی، بزرگی حرکات قیمت پایانی (Close) به سمت پایین و بالا را در L دوره گذشته محاسبه میکند و با مقایسه آنها با یکدیگر، به یک شاخص در خصوص موقعیت قیمت میرسد.
این اندیکاتور یک اسیلاتور است و بین 0 تا 100 نوسان میکند، درحالیکه مقادیر کمتر از 30 را بهعنوان نقاط «بیشفروش» (Oversold) و مقادیر بیشتر از 70 را به عنوان نقاط «بیشخرید» (Overbought) میشناسیم.
این اندیکاتور علاوه بر موارد گفته شده توانایی خوبی نیز در شناسایی «واگراییها» (Divergence) دارد و از این جهت نیز مهم است. بنابراین، یاد گرفتن روش کار و پیادهسازی آن، از جهات گوناگون میتواند به ما در تحلیل بازارها، ساخت استراتژیهای قدرتمند و ایجاد رباتهای معاملهگر کمک کند.
بدین منظور، ابتدا با روش محاسبه این اندیکاتور آشنا میشویم. اگر بازه زمانی از گام زمانی 1 شروع شود و تا T ادامه یابد، مجموعه قیمتهای پایانی را بهشکل زیر خواهیم داشت:
$$ c = \{c_1, c_2,\cdots , c_T\}$$
حال میتوانیم تغییرات قیمت را بین هر دو روز متوالی با فرمول زیر تعریف کنیم:
$$d_t=c_t-c_{t-1}$$
به این ترتیب، به سادگی میتوان متوجه شد که تغییرات قیمت تنها در بازه زمانی 2 تا T قابل محاسبه است:
$$ d = \{d_2, d_3,\cdots , d_T\}$$
در این بخش از محاسبه اندیکاتور، تغییرات قیمت را به دو سری جداگانه تقسیم میکنیم که اولی تحرکات به سمت بالا (Up Trend) و دومی تحرکات به سمت پایین (Down Trend) را ذخیره میکند. مقادیر این دو سری بهشکل زیر تعریف میشود:
- برای روزهای با افزایش قیمت، مقدار U برابر با تغییرات قیمت خواهد بود و مقدار D برابر با صفر خواهد بود.
- برای روزهای با کاهش قیمت، مقدار U برابر با صفر خواهد بود و مقدار D برابر با قرینه تغییرات قیمت خواهد بود.
بنابراین میتوان بهشکل زیر نوشت:
$$ \begin{aligned}
U_{t} &=\left\{\begin{array}{cc}
d_{t} & d_{t}>0 \\
0 & \text { otherwise }
\end{array}\right.\\
D_{t} &=\left\{\begin{array}{cc}
0 & d_{t}>0 \\
-d_{t} & \text { otherwise }
\end{array}\right.
\end{aligned} $$
البته میتوان با استفاده از تابع max این روابط را به شکل زیر نیز بازنویسی کرد:
$$ \begin{aligned}
U_{t} &=\max \left(d_{t}, 0\right) \\
D_{t} &=\max \left(-d_{t}, 0\right)
\end{aligned} $$
پس از محاسبه این دو سری، روی هر دو آنها یک «میانگین متحرک هموار» (Smoothed Moving Average) یا SMMA اعمال میکنیم. با تقسیم خروجی این دو میانگین متحرک، عدد جدیدی به نام «قدرت نسبی» (Relative Strength) یا SR یا «فاکتور قدرت نسبی» (Relative Strength Factor) یا RSF بهدست خواهد آمد:
$$ \begin{aligned}
R S_{t} &=\frac{\operatorname{SMMA}_{t}\left(U, L\right)}{\operatorname{SMMA}_{t}\left(D, L\right)}
\end{aligned} $$
این معیار میتواند عددی در بازه $$(0,+\infty)$$ به خود بگیرید که از آن میتوانیم برای محاسبه شاخص قدرت نسبی استفاده کنیم:
$$ \begin{aligned}
R S I_{t} &=100-\frac{100}{1+R S_{t}}
\end{aligned} $$
به این ترتیب، مقدار نهایی اندیکاتور قابل محاسبه است. توجه داشته باشید که با قرار دادن اعداد مختلف در بازه $$(0,+\infty)$$ بهجای RS میتوانیم به این نتیجه برسیم که RSI همواره در بازه $$(0,+100)$$ قرار خواهد گرفت.
میانگین متحرک هموار چیست؟
این میانگین متحرک نوع خاصی از میانگین متحرک نمایی (Exponential Moving Average) یا EMA است. برای آشنایی با این میانگین متحرک و پیادهسازی آن میتوانید به مطلب «پیاده سازی میانگین متحرک نمایی در پایتون – راهنمای گام به گام» مراجعه کنید. برای میانگین متحرک نمایی ابتدا یک L تعریف و سپس یک ضریب به نام $$\alpha$$ محاسبه میشود:
$$\alpha=\frac{1+r}{L+r} $$
سپس، با استفاده از این ضریب مقدار میانگین متحرک محاسبه میشود:
$$ E M A_{t}=(1-\alpha) \times E M A_{t-1}+\alpha \times \text { Close }_{t} $$
در اغلب موارد، از تنظیمات $$r=1$$ استفاده میشود. اگر تنظیمات $$r=0$$ استفاده شود، یک نوع خاصی از میانگین متحرک نمایی بهنام میانگین متحرک هموار حاصل خواهد شد که واکنش آرامتری نسبت به میانگین متحرک نمایی دارد. بنابراین میتوان گفت:
$$ \begin{aligned}
S M M A_{t}&=\frac{L-1}{L} \times S M M A_{t-1}+\frac{1}{L} \times \text { Close }_{t}=\frac{(L-1) \times S M M A_{t-1}+\text { Close }_{t}}{L} \\
&=S M M A_{t-1}+\frac{1}{L}\left(\text { Close }_{t}-\text { SMMA }_{t-1}\right)
\end{aligned} $$
به این ترتیب، برخی از مشکلات موجود در رابطه با تأخیر نیز حذف میشود.
پیاده سازی اندیکاتور RSI در پایتون
ابتدا کتابخانههای مورد نیاز را فراخوانی میکنیم:
1import numpy as np
2import yfinance as yf
3import matplotlib.pyplot as pltاین کتابخانهها، بهترتیب، برای موارد زیر استفاده خواهند شد:
- کار با آرایهها و محاسبات برداری
- 2. دریافت مجموعه داده مربوط به قیمت طلا
- رسم نمودارهای قیمت و اندیکاتور
تنظیمات زیر را نیز برای تغییر Style نمودارها اعمال میکنیم:
1plt.style.use('ggplot')حال میتوانیم مجموعه داده مربوط به قیمت طلا را، از تاریخ 2020/01/01 تا 2022/01/01 دریافت کنیم:
1DF = yf.download('GLD', start='2020-01-01', end='2022-01-01')برای بررسی اولیه مجموعه داده میتوانیم 5 سطر ابتدایی و 5 سطر انتهایی آن را نمایش دهیم:
1print(DF.head())
2
3print(DF.tail())که خواهیم داشت:
Open High Low Close Adj Close Volume Date 2019-12-31 143.309998 143.600006 142.800003 142.899994 142.899994 5313500 2020-01-02 143.860001 144.210007 143.399994 143.949997 143.949997 7733800 2020-01-03 145.750000 146.320007 145.399994 145.860001 145.860001 12272800 2020-01-06 148.440002 148.479996 146.949997 147.389999 147.389999 14403300 2020-01-07 147.570007 148.139999 147.429993 147.970001 147.970001 7978500 Open High Low Close Adj Close Volume Date 2021-12-27 168.960007 169.419998 168.779999 169.369995 169.369995 4760300 2021-12-28 169.330002 169.649994 168.619995 168.639999 168.639999 4541900 2021-12-29 167.360001 168.690002 167.279999 168.589996 168.589996 5889700 2021-12-30 168.429993 169.809998 168.369995 169.800003 169.800003 5426300 2021-12-31 170.529999 171.039993 170.039993 170.960007 170.960007 7039300
به این ترتیب، مشاهده میکنیم که مجموعه داده از تاریخ 2019/12/31 شروع و در تاریخ 2021/12/31 به اتمام رسیده است. برای پیادهسازی اندیکاتور شاخص قدرت نسبی، هم میتوانیم از امکانات کتابخانه Numpy و هم امکانات کتابخانه Pandas استفاده کنیم. ابتدا پیادهسازی به کمک Numpy را بررسی میکنیم. به همین دلیل، ستون مربوط به قیمت پایانی را بهشکل آرایه Numpy درمیآوریم:
1C = DF['Close'].to_numpy()حال میتوانیم یک آرایه دیگر نیز برای شماره روزها ایجاد کنیم:
1T = np.arange(start=1, stop=C.size + 1, step=1)توجه داشته باشید که تابع اعداد را در بازه start تا stop-step ایجاد میکند، بنابراین عدد C.size + 1 در این آرایه وجود نخواهد داشت. Size یکی از attributeهای آرایههای Numpy است که تعداد درایههای موجود در آرایه را نشان میدهد. برای دریافت اندازه بعد اول آرایهها میتوان از تابع len نیز استفاده کرد.
حال با کمک دو آرایه T و C میتوانیم یک نمودار نیمهلگاریتمی (Semi-logarithm) برای قیمت رسم کنیم:
1plt.semilogy(T, C, ls='-', lw=0.9, c='k')
2plt.title('Gold Price')
3plt.xlabel('Time (Day)')
4plt.ylabel('Price (USD)')
5plt.show()پس از اجرای کد، نمودار زیر را خواهیم داشت.
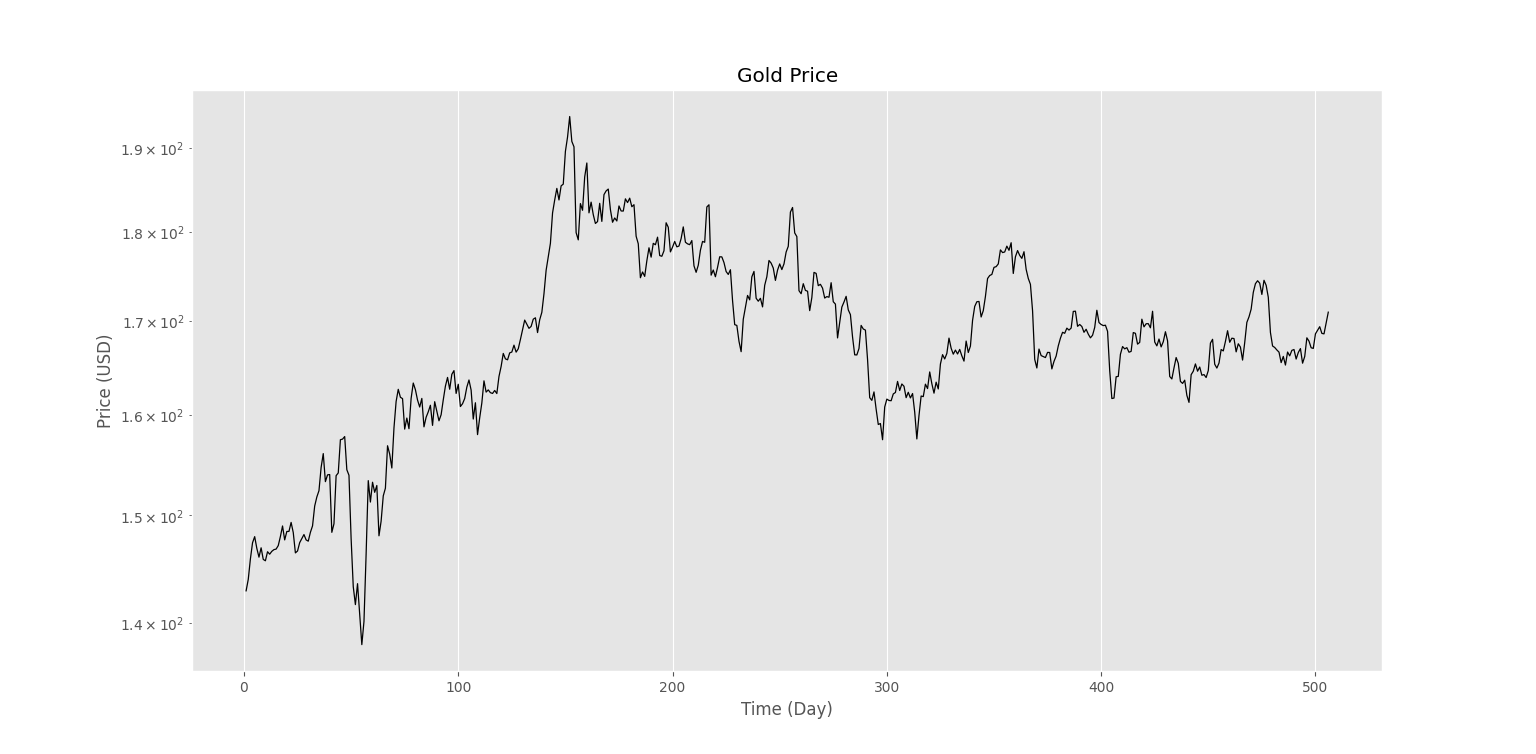
به این ترتیب، از صحت مجموعه داده اطمینان حاصل میکنیم. در نمودار قیمت برای برخی روزها سقف قیمت و رشد بسیار زیاد را مشاهده میکنیم. با توجه به روش محاسبه اندیکاتور شاخص قدرت نسبی، انتظار داریم که این نواحی به راحتی توسط آن شناسایی شود.
حال برای پیادهسازی اندیکاتور، یک تابع ایجاد میکنیم که در ورودی آرایه مربوط به قیمت پایانی و طول پنجره محاسبه اندیکاتور را دریافت میکند:
1def RSI(C:np.ndarray, L:int):حال در اولین قدم، اندازه داده ورودی را محاسبه میکنیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.sizeحال میتوانیم تعداد روزهایی را محاسبه کنیم که تغییرات قیمت برای آنها موجود است:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1حال دو آرایه با مقادیر برای U و D ایجاد میکنیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)سپس نیاز داریم تا یک حلقه ایجاد کنیم و برای هر مقدار از تغییرات قیمت، تصمیمگیری کنیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):در ابتدای حلقه، تغییرات قیمت را محاسبه میکنیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):
7 d = C[i + 1] - C[i]توجه داشته باشید که شمارش i از 0 شروع میشود بنابراین i-1 غیر قابلاستفاده است.
حال با یک شرط بررسی میکنیم تا اگر تغییرات قیمت مثبت بود، آن را به آرایه U اضافه کنیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):
7 d = C[i + 1] - C[i]
8 if d > 0:
9 U[i] = dدر غیر این صورت نیز، قرینه تغییرات به آرایه D اضافه خواهد شد:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):
7 d = C[i + 1] - C[i]
8 if d > 0:
9 U[i] = d
10 else:
11 D[i] = -dبه این ترتیب، دو سری U و D در انتهای حلقه کامل خواهد بود. حال میتوانیم میانگین متحرک هموار را بر روی این دو سری اعمال کنیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):
7 d = C[i + 1] - C[i]
8 if d > 0:
9 U[i] = d
10 else:
11 D[i] = -d
12 emaU = EMA(U, L, r=0)
13 emaD = EMA(D, L, r=0)توجه داشته باشید که ورودی r چون مقدار پیشفرض 1 را به خود میگیرد، برای تعیین مقداری غیر از آن، باید به شکل r=0 وارد شود.
به این ترتیب، سری RS قابل محاسبه خواهد بود:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):
7 d = C[i + 1] - C[i]
8 if d > 0:
9 U[i] = d
10 else:
11 D[i] = -d
12 emaU = EMA(U, L, r=0)
13 emaD = EMA(D, L, r=0)
14 RS = emaU / emaDدر نهایت نیز RSI را محاسبه میکنیم و برمیگردانیم:
1def RSI(C:np.ndarray, L:int):
2 nD0 = C.size
3 nD1 = nD0 - 1
4 U = np.zeros(nD1)
5 D = np.zeros(nD1)
6 for i in range(nD1):
7 d = C[i + 1] - C[i]
8 if d > 0:
9 U[i] = d
10 else:
11 D[i] = -d
12 emaU = EMA(U, L, r=0)
13 emaD = EMA(D, L, r=0)
14 RS = emaU / emaD
15 rsi = 100 - 100 / (1 + RS)
16 return rsiبه این ترتیب، تابع RSI تکمیل میشود.
برای تابع EMA نیز از تابع زیر استفاده میکنیم:
1def EMA(S:np.ndarray, L:int, r:float=1):
2 a = (1 + r) / (L + r)
3 nD0 = S.size
4 nD = nD0 - L + 1
5 M = np.zeros(nD)
6 M[0] = np.mean(S[:L])
7 for i in range(1, nD):
8 M[i] = a * S[i + L - 1] + (1 - a) * M[i - 1]
9 return Mتوجه داشته باشید که میتوانیم خود تابع SMMA را به شکل جداگانه نیز تعریف کنیم:
1def SMMA(S:np.ndarray, L:int):
2 nD0 = S.size
3 nD = nD0 - L + 1
4 M = np.zeros(nD)
5 M[0] = np.mean(S[:L])
6 for i in range(1, nD):
7 M[i] = (S[i + L - 1] + (L - 1) * M[i - 1]) / L
8 return Mاین تابع مشابه قبلی است با این تفاوت که مقدار r برای آن متغیر نبوده و همواره 0 است. کد زیر نیز میتواند به عنوان جایگزین برای حالت قبلی استفاده شود:
1def SMMA(S:np.ndarray, L:int):
2 M = EMA(S, L, r=0)
3 return Mنکته مهمی که وجود دارد، کاهش سرعت برنامه در صورت استفاده تودرتو از توابع است که باید در پروژههای بزرگ مورد توجه قرار گیرد. حال میتوانیم از تابع پیادهسازی شده استفاده کرده و اندیکاتور را محاسبه کنیم:
1rsi = RSI(C, 14)در نتیجه، اندیکاتور شاخص قدرت نسبی در طول پنجره 14 روزه محاسبه و برگردانده خواهد شد. برای نمایش نتایج، دو نمودار مربوط به قیمت و اندیکاتور را در کنار هم رسم میکنیم تا عملکرد آن را مشاهده کنیم:
1plt.subplot(3, 1, (1, 2))
2plt.semilogy(T, C, ls='-', lw=0.9, c='k')
3plt.title('Gold Price')
4plt.ylabel('Price (USD)')
5plt.tight_layout()
6
7plt.subplot(3, 1, 3)
8plt.plot(T[-rsi.size:], rsi, ls='-', lw=0.8, c='crimson')
9plt.title('Relative Strength Index (RSI)')
10plt.xlabel('Time (Day)')
11plt.ylabel('RSI')
12plt.tight_layout()
13
14plt.show()توجه داشته باشید که در تابع plt.subplot 3 سطر و 1 ستون تعیین شده است، اما دو سطر اول برای نمودار قیمت در نظر گرفته شدهاند.
نکته مهم دیگری که باید به آن توجه کرد در خصوص طول آرایه rsi است. این آرایه طولی برابر با C و T ندارد، بنابراین نمیتوان از T بهعنوان مقادیر زمان استفاده کرد و حالت T[-rsi.size:] صحیح خواهد بود. پس از رسم نمودار فوق، نتیجه زیر حاصل میشود.
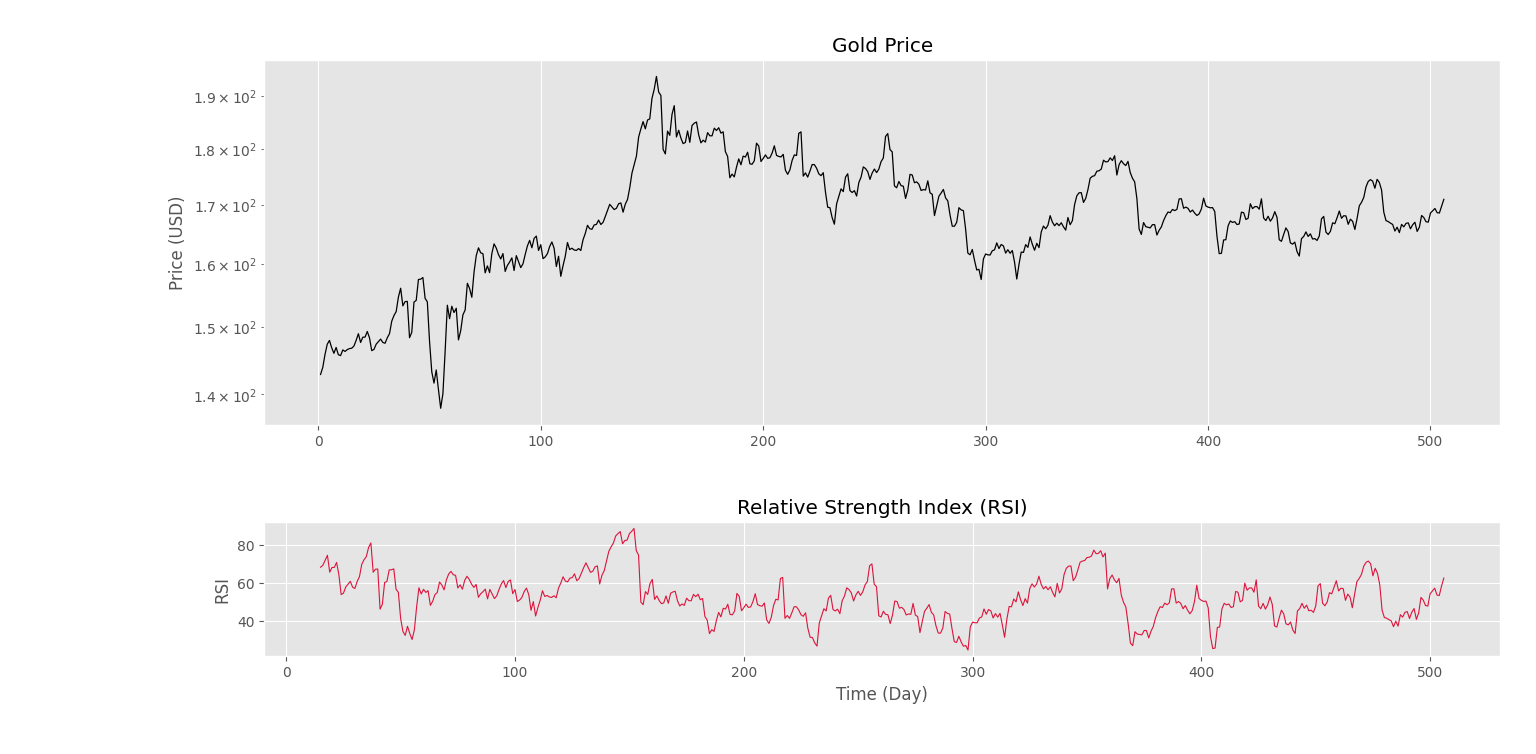
بنابراین، نمودار رسم میشود. مشکل دیگری که وجود دارد، بههمریختگی محور افقی دو نمودار به دلیل تفاوت در طول آن دو است. برای رفع این مشکل از plt.xlim استفاده میکنیم:
1plt.subplot(3, 1, (1, 2))
2plt.semilogy(T, C, ls='-', lw=0.9, c='k')
3plt.title('Gold Price')
4plt.ylabel('Price (USD)')
5plt.xlim(left=0, right=C.size + 1)
6plt.tight_layout()
7
8plt.subplot(3, 1, 3)
9plt.plot(T[-rsi.size:], rsi, ls='-', lw=0.8, c='crimson')
10plt.title('Relative Strength Index (RSI)')
11plt.xlabel('Time (Day)')
12plt.ylabel('RSI')
13plt.xlim(left=0, right=C.size + 1)
14plt.tight_layout()
15
16plt.show()توجه داشته باشید که اضافه کردن این تکه کد به هر دو نمودار الزامی است. رعایت کردن یک حاشیه در سمت چپ و راست نیز برای مناسب بودن نمودار الزامی است. حال با اجرای برنامه نمودار شکل زیر ظاهر خواهد شد.
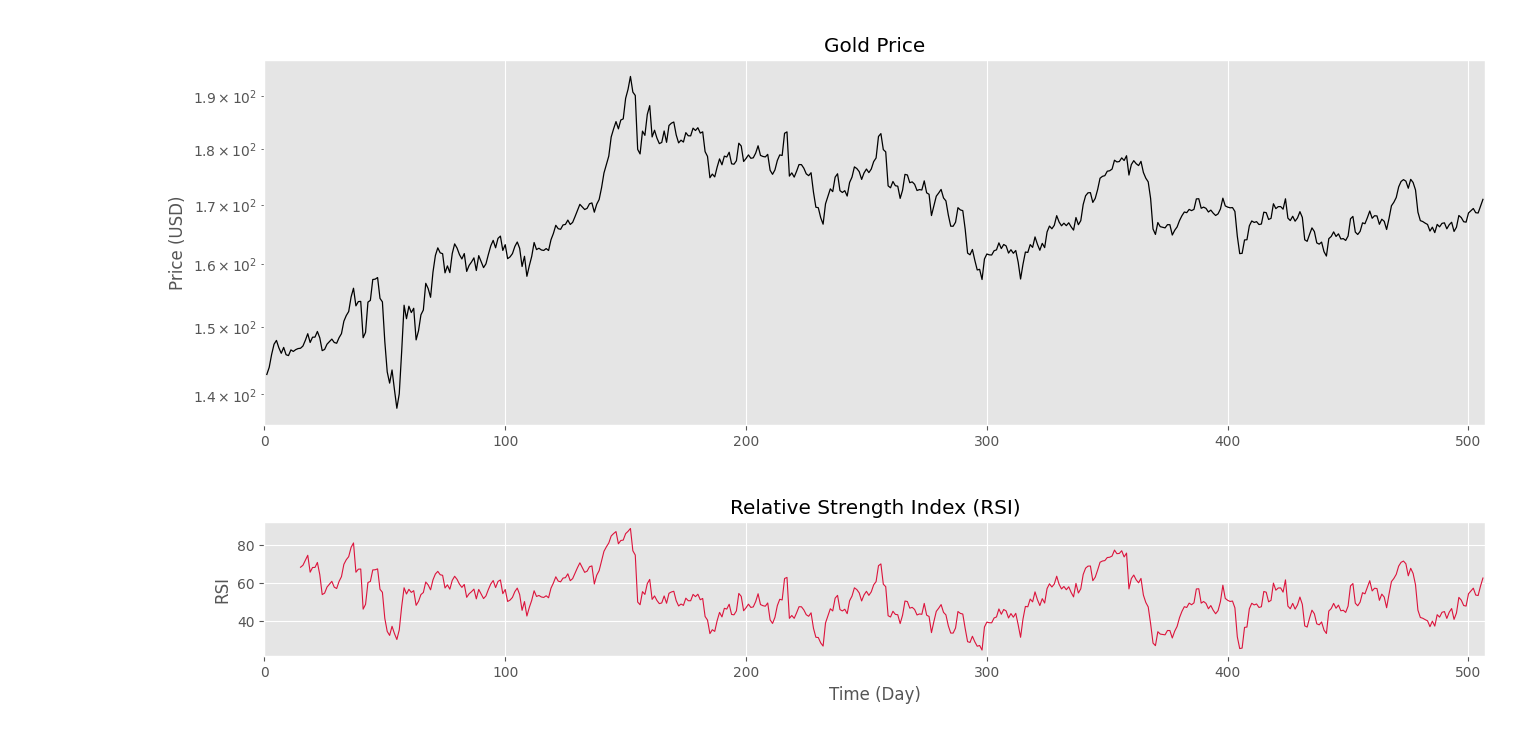
به این ترتیب، بههمریختگی محور افقی رفع میشود. حال میتوانیم نمودار پایینی را نیز بین 0 تا 100 محدود کنیم و دو خط 30 و 70 نیز به آن اضافه کنیم:
1plt.subplot(3, 1, (1, 2))
2plt.semilogy(T, C, ls='-', lw=0.9, c='k')
3plt.title('Gold Price')
4plt.ylabel('Price (USD)')
5plt.xlim(left=0, right=C.size + 1)
6plt.tight_layout()
7
8plt.subplot(3, 1, 3)
9plt.plot(T[-rsi.size:], rsi, ls='-', lw=0.8, c='crimson')
10plt.axhline(30, ls='-', lw=0.7, c='teal')
11plt.axhline(70, ls='-', lw=0.7, c='teal')
12plt.title('Relative Strength Index (RSI)')
13plt.xlabel('Time (Day)')
14plt.ylabel('RSI')
15plt.xlim(left=0, right=C.size + 1)
16plt.ylim(bottom=0, top=100)
17plt.yticks([0, 30, 50, 70, 100], [0, 30, 50, 70, 100])
18plt.tight_layout()
19
20plt.show()در نهایت، شکل نهایی نمودار حاصل خواهد شد.
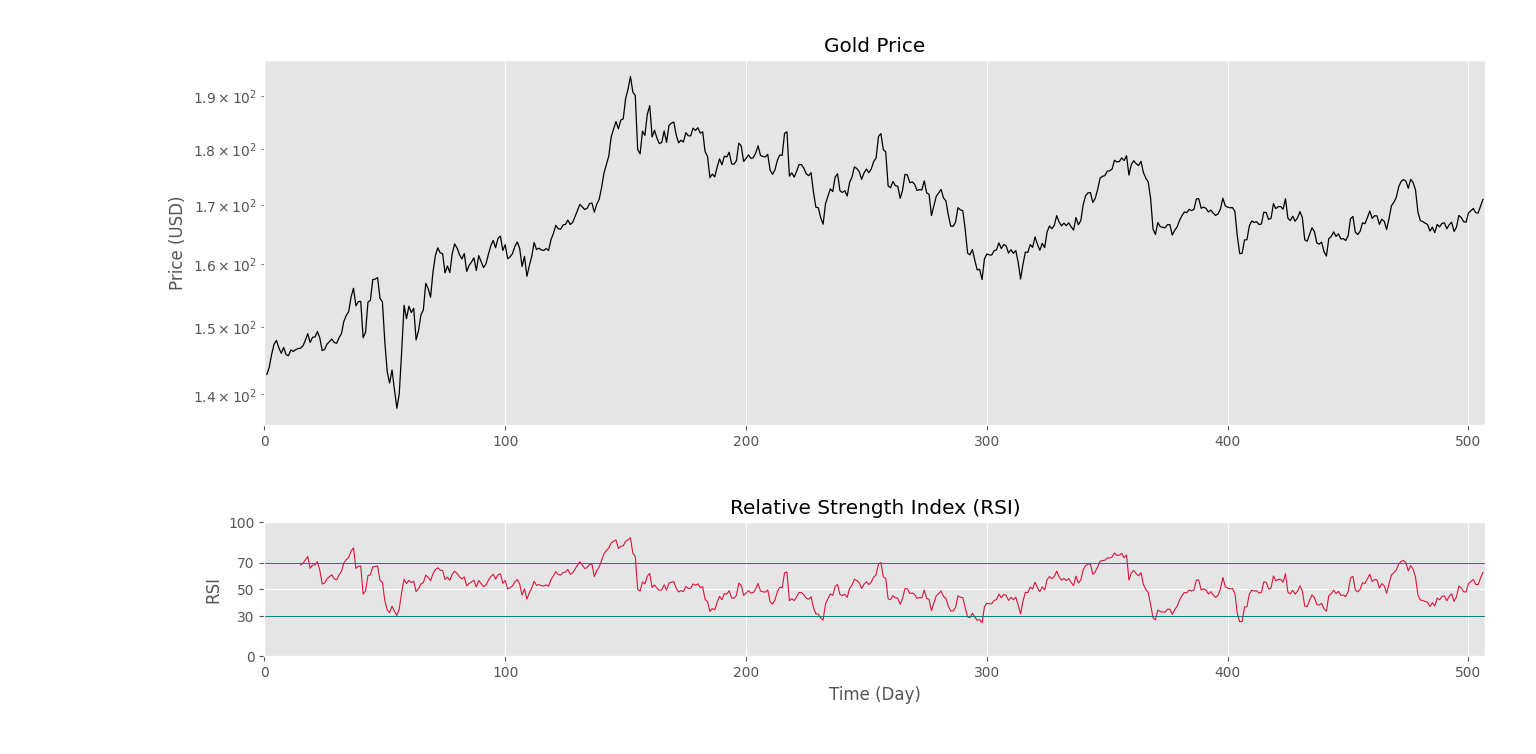
به این ترتیب، نمودار کامل میشود. حال میتوان بررسی کرد دید که اندیکاتور نقاط بیشخرید را در روزهای 40، 140 و 350 تشخیص داده است. برخی نقاط بیشفروش کوچک نیز شناسایی شدهاند که واکنش معاملهگران و بازگشت قیمت را شاهد بودهایم. بنابراین، اندیکاتور با استفاده از امکانات کتابخانه Numpy پیادهسازی و نتایج مصورسازی شدند.
حال قصد داریم اندیکاتور را به کمک کتابخانه Pandas پیادهسازی کنیم. برای این منظور فراخوانی زیر را نیز به موارد قبلی اضافه میکنیم:
1import pandas as pdابتدا تابع را ایجاد و در ورودی دیتافریم و طول پنجره را دریافت میکنیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):حال در اولین مرحله یک ستون برای تغییرات قیمت هر دو روز متوالی ایجاد میکنیم و با کمک متد diff آن را محاسبه میکنیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()حال میتوانیم دو ستون U و D را به کمک متد apply محاسبه کنیم. به این منظور از توابع lambda پایتون استفاده میکنیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()
3 DF['U'] = DF['d'].apply(lambda x: max(x, 0))
4 DF['D'] = DF['d'].apply(lambda x: max(-x, 0))حال باید میانگین متحرک هموار را بر روی دو ستون اخیر اعمال کنیم. برای این منظور، میتوانیم از متد ewm استفاده کنیم و در نهایت میانگینگیری کنیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()
3 DF['U'] = DF['d'].apply(lambda x: max(x, 0))
4 DF['D'] = DF['d'].apply(lambda x: max(-x, 0))
5 DF['smmaU'] = DF['U'].ewm(com=L - 1).mean()
6 DF['smmaD'] = DF['D'].ewm(com=L - 1).mean()توجه داشته باشید که متد ewm به چندین شکل میتواند ورودی دریافت که یکی از آنها به کمک com است و به شکل زیر عمل میکند:
$$ \alpha = \frac 1 { 1 + \text{com}} $$
به این ترتیب، برای اینکه تنظیمات $$\alpha = \frac 1 L $$ را داشته باشیم، باید مقدار com برابر با L-1 باشد. حال میتوانیم ستون RS را از نسبت دو ستون اخیر حساب کنیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()
3 DF['U'] = DF['d'].apply(lambda x: max(x, 0))
4 DF['D'] = DF['d'].apply(lambda x: max(-x, 0))
5 DF['smmaU'] = DF['U'].ewm(com=L - 1).mean()
6 DF['smmaD'] = DF['D'].ewm(com=L - 1).mean()
7 DF['RS'] = DF['smmaU'] / DF['smmaD']در نهایت، میتوانیم خود اندیکاتور را محاسبه کنیم و پیادهسازی تابع به اتمام برسد:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()
3 DF['U'] = DF['d'].apply(lambda x: max(x, 0))
4 DF['D'] = DF['d'].apply(lambda x: max(-x, 0))
5 DF['smmaU'] = DF['U'].ewm(com=L - 1).mean()
6 DF['smmaD'] = DF['D'].ewm(com=L - 1).mean()
7 DF['RS'] = DF['smmaU'] / DF['smmaD']
8 DF['RSI'] = 100 - 100 / (1 + DF['RS'])حال میتوانیم تابع را روی دیتافریم اعمال کنیم:
1RSI(DF, 14)پس از اجرای این بخش از کد، 7 ستون جدید به دیتافریم اضافه خواهد شد که تنها 1 ستون از آنها مورد نیاز است، برای بهینگی برنامه میتوانیم در انتهای تابع این ستونهای اضافه را حذف کنیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()
3 DF['U'] = DF['d'].apply(lambda x: max(x, 0))
4 DF['D'] = DF['d'].apply(lambda x: max(-x, 0))
5 DF['smmaU'] = DF['U'].ewm(com=L - 1).mean()
6 DF['smmaD'] = DF['D'].ewm(com=L - 1).mean()
7 DF['RS'] = DF['smmaU'] / DF['smmaD']
8 DF['RSI'] = 100 - 100 / (1 + DF['RS'])
9 DF.drop(['d', 'U', 'D', 'smmaU', 'smmaD', 'RS'], axis=1, inplace=True)به این ترتیب، 6 ستون اضافه حذف خواهند شد. مشکل دیگری که در رابطه با این تابع وجود دارد، احتمال محاسبه چندین RSI است. برای مثال، اگر بخواهیم دو RSI با طولهای متفاوت ایجاد کنیم، تنها یکی از آنها را خواهیم داشت. برای رفع این مشکل، بهتر است نامگذاری هر ستون RSI را با طول آن تعیین کنیم تا مشکلی ایجاد نشود. برای این منظور، تابع را با اندکی تغییر به شکل زیر تغییر میدهیم:
1def RSI(DF:pd.core.frame.DataFrame, L:int):
2 DF['d'] = DF['Close'].diff()
3 DF['U'] = DF['d'].apply(lambda x: max(x, 0))
4 DF['D'] = DF['d'].apply(lambda x: max(-x, 0))
5 DF['smmaU'] = DF['U'].ewm(com=L - 1).mean()
6 DF['smmaD'] = DF['D'].ewm(com=L - 1).mean()
7 DF['RS'] = DF['smmaU'] / DF['smmaD']
8 DF[f'RSI({L})'] = 100 - 100 / (1 + DF['RS'])
9 DF.drop(['d', 'U', 'D', 'smmaU', 'smmaD', 'RS'], axis=1, inplace=True)به این ترتیب، هر RSI ستونی با نام اختصاصی برای خود خواهد داشت. حال میتوانیم پس از اعمال تابع بر روی دیتافریم، نمودار مربوط به اندیکاتور را رسم کنیم. به این منظور، کد قبلی را با اندکی تغییر به شکل زیر تغییر میدهیم:
1plt.subplot(3, 1, (1, 2))
2plt.semilogy(DF.index, DF.Close, ls='-', lw=0.9, c='k')
3plt.title('Gold Price')
4plt.ylabel('Price (USD)')
5plt.xlim(left=DF.index[0], right=DF.index[-1])
6plt.tight_layout()
7
8plt.subplot(3, 1, 3)
9plt.plot(DF.index, DF['RSI(14)'], ls='-', lw=0.8, c='crimson')
10plt.axhline(30, ls='-', lw=0.7, c='teal')
11plt.axhline(70, ls='-', lw=0.7, c='teal')
12plt.title('Relative Strength Index (RSI)')
13plt.xlabel('Time (Day)')
14plt.ylabel('RSI')
15plt.xlim(left=DF.index[0], right=DF.index[-1])
16plt.ylim(bottom=0, top=100)
17plt.yticks([0, 30, 50, 70, 100], [0, 30, 50, 70, 100])
18plt.tight_layout()
19
20plt.show()در نهایت، خروجی به شکل زیر حاصل خواهد شد.
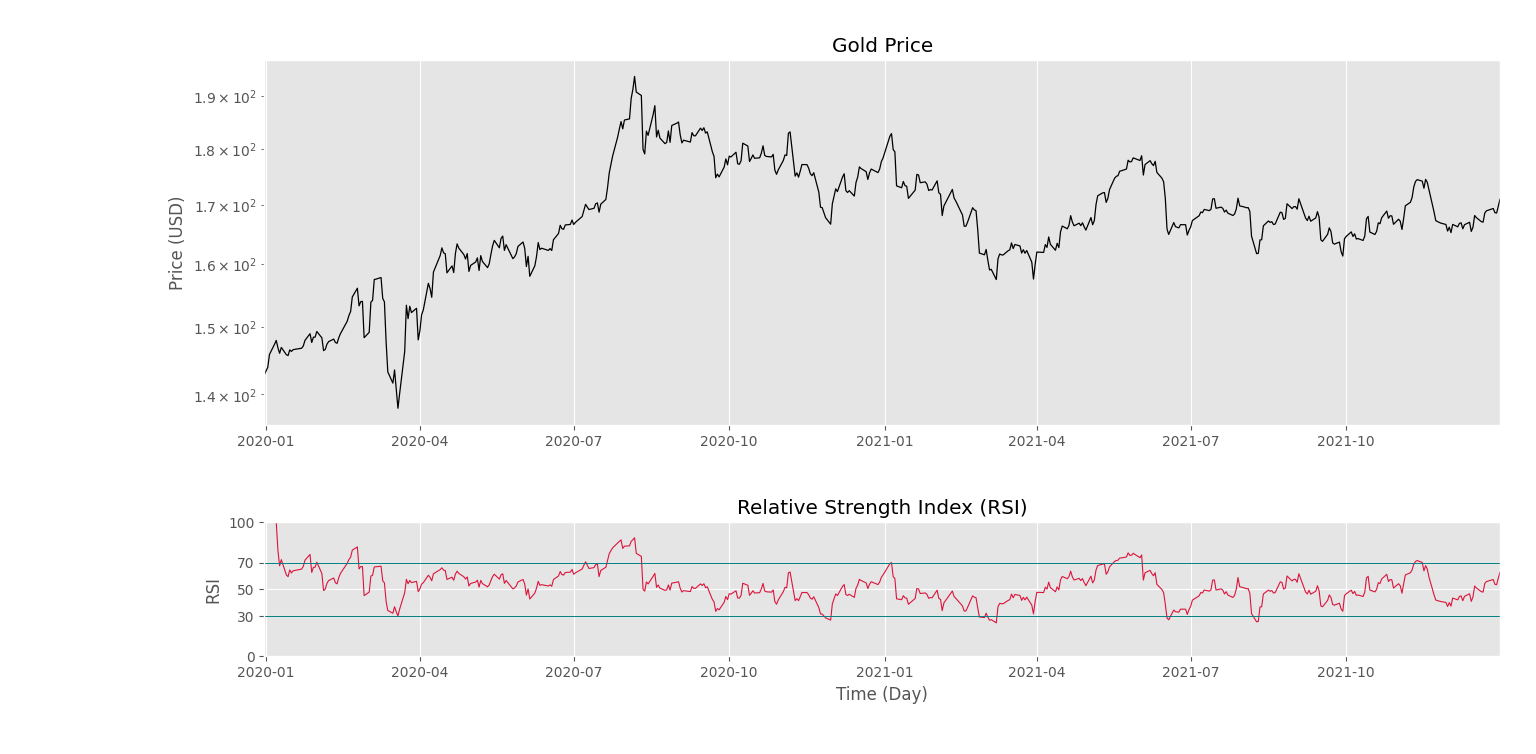
بنابراین، مشاهده میکنیم که نتیجه کاملاً مشابه پیادهسازی قبلی است. بنابراین هر دو کتابخانه امکاناتی برای اینگونه پیادهسازیها ارائه میکنند که هرکدام میتواند تحت شرایطی گزینه مناسبی باشد.
جمعبندی اندیکاتور RSI در پایتون
پیادهسازی اندیکاتور شاخص قدرت نسبی در اینجا به اتمام میرسد. برای مطالعه بیشتر میتوان موارد زیر را بررسی کرد:
- اگر به جای SMMA از EMA ساده در هموارسازی استفاده کنیم، چه تغییری حاصل خواهد شد؟ در یک نمودار این تغییرات را نشان دهید.
- چرا کتابخانه Pandas برای 13 روز اول اندیکاتور نیز مقدار میدهد ولی Numpy نمیتواند؟
- متد ewm را از سایت رسمی کتابخانه Pandas بررسی و انواع روشهای فراخوانی آن را مطالعه کنید.
- چگونه میتوان شاخص قدرت نسبی را به بازه محدود کرد؟
- اگر بخواهیم از این اندیکاتور برای ایجاد یک ربات معاملهگر ساده استفاده کنیم، چه استراتژیهای قابل استفاده خواهد بود؟
- ورودی inplace در متد drop چه فرآیندی را کنترل میکند؟
- سه خط smmaU, smmaD, RSI را در کنار هم رسم کنید بررسی کنید چه ارتباطی با هم دارند؟
- چگونه میتوان به کمک مقادیر smmaU، smmaD و قیمت پایانی میتوان شدت روند موجود در بازار را محاسبه کرد؟










