تندی متوسط چیست؟ – یکا و فرمول به زبان ساده

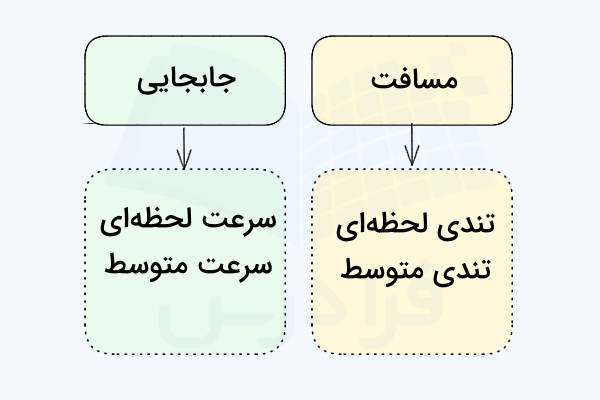
حرکت اجسام در فیزیک و توصیف آن از اهمیت بالایی برخوردار است. حرکت جسمی مشخص در فیزیک توسط کمیت‌هایی مانند تندی، سرعت، جابجایی و شتاب، توصیف می‌شود. تندی و سرعت دو کمیتی هستند که در بیشتر مواقع به جای یکدیگر استفاده می‌شوند. اما باید بدانیم این دو کمیت با یکدیگر تفاوت دارند. تندی متوسط کمیتی نرده‌ای است که تنها اندازه دارد و از تقسیم مسافت بر مدت زمان لازم برای طی کردن آن مسافت به‌دست می‌آید. در این مطلب از مجله فرادرس با تندی متوسط آشنا می‌شویم و به پرسش تندی متوسط چیست به زبان ساده پاسخ می‌دهیم.

پس از تعریف تندی متوسط، فرمول‌ محاسبه تندی متوسط را بیان و چگونگی محاسبه این کمیت را با حل مثال‌های مختلف بررسی می‌کنیم. در ادامه، تفاوت تندی متوسط و سرعت متوسط را توضیح می‌دهیم. در پایان، تندی متوسط در حرکت بر خط راست و حرکت دایره‌ای و چگونگی محاسبه آن در هر حرکت را بررسی می‌کنیم.

تندی متوسط چیست؟

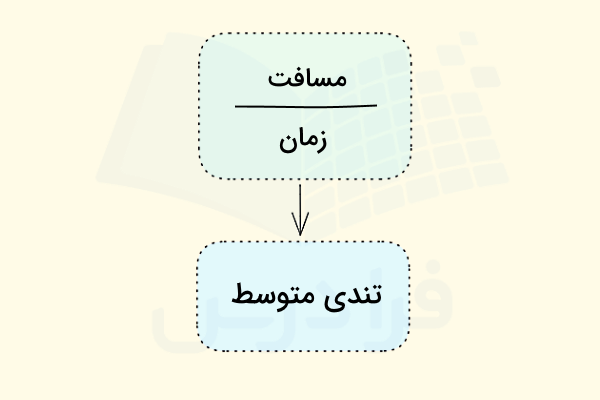
به نسبت «مسافت» (Distance | D) طی شده توسط جسم به مدت زمان لازم برای طی کردن آن مسافت، «تندی متوسط» (Average Speed | $$\overline { S }$$) گفته می‌شود. کلمه متوسط در تندی متوسط، بسیار شبیه محاسبه معدل در دوران مدرسه است. فرمول تندی متوسط به شکل زیر است:

مدت زمان لازم برای طی کردن مسافت / مسافت = تندی متوسط

در ادامه برای درک مفهوم این کمیت، تندی متوسط اتومبیل زردرنگ نشان داده شده در تصویر زیر را به‌دست می‌‌آوریم.

راننده این اتومبیل برای خرید تعدادی وسایل از خانه خارج می‌شود و مسیرهای زیر را به ترتیب طی می‌کند:

• او ابتدا برای خرید مقداری میوه، پنج کیلومتر به سمت شرق رانندگی می‌کند.
• سپس، برای خرید نان، یک کیلومتر به سمت شمال رانندگی می‌کند.
• در ادامه، برای خرید وسایل آشپزخانه به فروشگاهی در ۹ کیلومتری نانوایی می‌رود. فروشگاه در جنوب‌شرقی نانوایی قرار گرفته است.
• در پایان، راننده پس از ۱۵ کیلومتر رانندگی و گذشتن از چندین خیابان و کوچه، به خانه می‌رسد.
• مدت زمان کل خرید برابر ۳ ساعت است.

برای محاسبه تندی متوسط، ابتدا کل مسافت طی شده توسط اتومبیل را به‌دست می‌آوریم. مسافت کلِ طی شده توسط اتومبیل در مدت زمان ۳ ساعت برابر است با:

$$D = 5 + 1 + 9 + 15 = 30 \ km$$

در ادامه، مسافت طی شده را بر مدت زمان لازم برای طی کردن آن مسافت، تقسیم کنیم.

$$speed = \frac{30 \ km}{ 3 h} = 10 \ \frac{km}{h}$$

تندی متوسط برابر ۱۰ کیلومتر بر ساعت است. سوالی که ممکن است مطرح شود آن است که آیا این اتومبیل در هر ساعت، ۱۰ کیلومتر حرکت می‌کند. خیر، تندی متوسط به ما میانگین تندی را در مدت زمان حرکت می‌دهد. ممکن است اتومبیل مسیر خانه تا میوه‌فروشی را در مدت زمان ۱۵ دقیقه طی کرده، اما به هنگام رفتن به نانوایی با ترافیک شدیدی مواجه شده و مسیر یک کیلومتری را در مدت نیم ساعت طی کرده باشد. بنابراین، اتومبیل با تندی یکسانی حرکت نکرده است. در اینجا، تندی را در تمام طول مسیر به‌دست آوردیم.

نکته ۱: برای به‌دست آوردن تندی متوسط باید مسافت کل طی شده توسط جسم را بر مدت زمان طی کردن آن مسافت، تقسیم کنیم.

نکته ۲: از آنجا که مسافت کمیتی نرده‌ای است و تنها اندازه دارد، تندی نیز کمیتی نرده‌ای است.

همان‌طور که در ابتدای این بخش گفتیم، تندی متوسط از تقسیم مسافت کل بر مدت زمان لازم برای طی کردن آن مسافت، به‌دست می‌آید. برای داشتن درک بهتری از مفهوم تندی متوسط، مسافت را تعریف و تفاوت آن را با جابجایی توضیح می‌دهیم.

مسافت چیست؟

بار دیگر مثال اتومبیل زردرنگ را بخوانید. راننده اتومبیل برای خرید تعدادی وسایل از خانه خارج می‌شود و پس از طی کردن مسیری مشخص، به خانه برمی‌گردد. مسیر حرکت این اتومبیل در تصویر زیر نشان داده شده است:

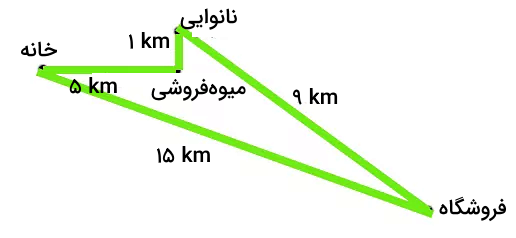
به هنگام محاسبه مسافت، کل مسیر طی شده توسط جسم برای ما مهم است. مسیر طی شده توسط اتومبیل با استفاده از خطوط سبزرنگ در تصویر زیر نشان داده شده است. برای محاسبه مسافت، باید طول این خطوط را با یکدیگر جمع کنیم. در نتیجه، به کل مسیر طی شده توسط جسم، مسافت گفته می‌شود. راننده اتومبیل پس از خروج از منزل و بازگشت به آن، مسافتی برابر ۳۰ کیلومتر را طی کرده است.

جابجایی چیست؟

جابجایی، برخلاف مسافت، کمیتی برداری است و اندازه و جهت دارد. مثال اتومبیل زردرنگ را در نظر بگیرید. برای محاسبه جابجایی این اتومبیل، تنها کافی است به نقاط ابتدایی و انتهایی و فاصله بین آن‌ها توجه کنیم. بردار جابجایی، برداری است که ابتدای آن نقطه آغاز حرکت و انتهای آن، نقطه پایان حرکت است. جابجایی اتومبیل زردرنگ چه مقدار است؟ جابجایی اتومبیل در مثال فوق، برابر صفر است. چرا؟ زیرا نقطه‌های ابتدا و انتهای حرکت یکسان هستند. راننده پس از خارج شدن از خانه و خرید وسایل لازم، دوباره به خانه برمی‌گردد.

نکته: به هنگام حل مسائل مربوط به جابجایی، جهتی را به عنوان جهت مثبت انتخاب می‌کنیم. اگر جهت حرکت جسم و جهت مثبت انتخاب شده، یکسان باشند، بردار جابجایی برداری مثبت است. اما اگر اتومبیل در خلاف جهت مثبت حرکت کند، بردار جابجایی به عنوان برداری منفی در نظر گرفته می‌شود.

فرمول تندی متوسط چیست؟

در بخش قبل فهمیدیم تندی متوسط چیست و چگونه به‌دست می‌آید. تندی متوسط از تقسیم مسافت کل بر مدت زمان صرف شده برای طی کردن مسافت محاسبه می‌شود:

مدت زمان لازم برای طی کردن مسافت / مسافت = تندی متوسط

یکای تندی متوسط چیست؟

گاهی کمیت‌های نرده‌ای، مانند تندی، برحسب کمیت‌های نرده‌ای دیگری نوشته می‌شوند. در این حالت، برای آن‌که بتوانیم واحد اندازه‌گیری کمیت نرده‌ای را به‌دست آوریم، گام‌های زیر را طی می‌کنیم:

• فرمول کمیت فیزیکی موردنظر را می‌نویسیم.

$$\overline { s } = \frac { distance } { total \ time }$$

در رابطه فوق، distance به معنای مسافت و total time به معنای زمان کل برای طی کردن مسافت است.

• واحدها یا یکاهای اندازه‌گیری همه کمیت‌ها (مسافت و زمان) را به شکل بنیادی یا استاندارد آن‌ها جایگزین می‌کنیم. در اینجا، سیستم SI به عنوان سیستم اندازه‌گیری استاندارد انتخاب می‌شود. واحد اندازه‌گیری مسافت و زمان در سیستم SI به ترتیب برابر متر و ثانیه است.
• پس از ساده‌سازی، واحد کمیت موردنظر به‌دست می‌آید.

$$SI \ unit \ of \ velocity = \frac { SI\ unit\ of\ displacement} { SI\ unit\ of\ time} \\ SI \ unit \ of\ velocity = \frac { m} { s}$$

توجه به این نکته مهم است که در مسافت‌ها و زمان‌های طولانی، یکای تندی ممکن است به صورت کیلومتر بر ساعت نیز بیان شود.

مثال تبدیل متر بر ثانیه به کیلومتر بر ساعت

اتومبیلی با تندی ۲۰ متر بر ثانیه حرکت می‌کند. تندی آن برحسب کیلومتر بر ساعت چه مقدار است؟

پاسخ

برای تبدیل متر بر ثانیه به کیلومتر بر ساعت، باید دو تبدیل زیر را در نظر داشته باشیم:

$$1 \ m = \frac { 1 } { 1000 } \ km , \enspace 1 \ sec = \frac { 1 } { 3600 } \ hour$$

با استفاده از دو رابطه فوق، به راحتی می‌توانیم تندی ۲۰ متر بر ثانیه را به کیلومتر بر ساعت تبدیل کنیم:

$$20 \ \frac { m } { s } = 20 \times \ \frac { \frac { 1 } { 1000 } } { \frac { 1 } { 3600 } } \ \frac { km } { h } = 20 \times \frac { 3600 } { 1000 } \ \frac { km } { h } = 20 \times \frac { 18 } { 5 } = 72 \ \frac { km } { h }$$

مثال تبدیل کیلومتر بر ساعت به متر بر ثانیه

اتومبیلی با تندی ۷۲ کیلومتر بر ساعت حرکت می‌کند. تندی آن برحسب متر بر ثانیه چه مقدار است؟

پاسخ

برای تبدیل کیلومتر بر ساعت به متر بر ثانیه، باید دو تبدیل زیر را در نظر داشته باشیم:

$$1 \ km = 1000 \ m , \enspace 1 \ h = 3600 \ s$$

با استفاده از دو رابطه فوق، به راحتی می‌توانیم تندی ۷۲ کیلومتر بر ساعت را به متر بر ثانیه تبدیل کنیم:

$$72 \ \frac { km } { h } = 72 \times \ \frac { { 1000 } } { { 3600 } } \ \frac { m } { s } = 72 \times \frac { 10} { 36 } \ \frac { m } { s } = 72 \times \frac { 5 } { 18 } \frac{ m } { s } = 20 \ \frac { m } { s }$$

تا اینجا فهمیدیم مفهوم تندی متوسط چیست و با تعریف مسافت، جابجایی و تفاوت آن‌ها با یکدیگر آشنا شدیم. در ادامه، سرعت متوسط را تعریف و تفاوت آن با تندی متوسط را توضیح می‌دهیم.

سرعت متوسط چیست و چه تفاوتی با تندی متوسط دارد؟

در مطالب بالا به پرسش تندی متوسط چیست، پاسخ دادیم. تندی متوسط را به صورت مسافت بر مدت زمان طی کردن مسافت، تعریف کردیم. تندی متوسط هر جسمی همواره بزرگ‌تر یا برابر سرعت متوسط است. دلیل این موضوع به تفاوت مفهوم مسافت و جابجایی برمی‌گردد. مسافت، همواره افزایشی است، اما جهت جابجایی می‌تواند تغییر کند و اندازه آن نیز ممکن است افزایش یا کاهش یابد. هنگامی که در مورد سرعت صحبت می‌کنیم، به مسافت طی شده توسط جسم کاری نداریم، بلکه به جابجایی آن توجه می‌کنیم. بار دیگر مثال اتومبیل زردرنگ را در نظر می‌گیریم. فرض کنید راننده پس از ۱۵ دقیقه به مغازه میوه‌فروشی، پس از نیم ساعت به نانوایی، پس از یک ساعت به فروشگاه و پس از یک ساعت و ۱۵ دقیقه به خانه می‌رسد.

اتومبیل در ابتدا کجا بود؟ در خانه. مکان آن پس از گذشت ۴۵ دقیقه کجا است؟ نانوایی. اتومبیل در مدت ۴۵ دقیقه، چه مسافتی را طی کرده است؟ ۶ کیلومتر. جابجایی اتومبیل در این مدت چه مقدار است؟ برای محاسبه جابجایی در این مدت، ابتدا نقاط ابتدا و انتهای مسیر را مشخص، سپس بردار جابجایی را رسم و طول آن را محاسبه می‌کنیم. نقطه ابتدای مسیر، خانه و نقطه انتهای مسیر،‌ نانوایی است. در نتیجه، بردار جابجایی به صورت زیر رسم می‌شود:

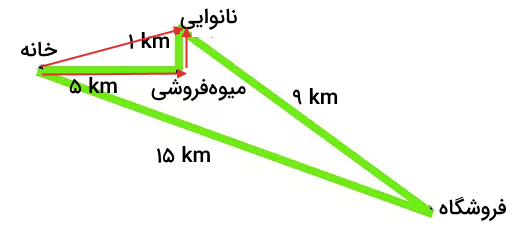
بردار جابجایی اتومبیل، وتر مثلثِ قائم‌الزاویه‌ای است که از بردارهای قرمزرنگ تشکیل شده است. برای محاسبه مقدار آن از قضیه فیثاغورت استفاده می‌کنیم.

$$Displacement = \sqrt { ( 5 \ km ) ^ 2 + (1 \ km ) ^ 2 } = \sqrt { 25 + 1 } = \sqrt { 26 } = 5.1 \ km$$

مسافت طی شده توسط اتومبیل در ۴۵ دقیقه اول حرکت، برابر ۶ کیلومتر و جابجایی آن برابر ۵٫۱ کیلومتر است. به این نکته توجه داشته باشید که به هنگام صحبت در مورد جابجایی، نه‌تنها مقدار آن، بلکه جهت جابجایی نیز باید در نظر گرفته شود. بنابراین سرعت متوسط به صورت زیر به‌دست می‌آید:

$$\overline { v } = \frac { \triangle x } { \triangle t }$$

تفاوت اصلی بین سرعت و تندی آن است که تندی کمیتی نرده‌ای، اما سرعت کمیتی برداری است. دلیل این موضوع آن است که مسافت طی شده توسط جسم، کمیتی نرده‌ای است و به مسیر حرکت جسم بستگی دارد. اما جابجایی کمیتی برداری و تنها به نقاط ابتدا و انتهای حرکت، وابسته است.

چگونه تندی متوسط را بهتر یاد بگیریم؟

در بخش‌های قبل فهمیدیم تندی متوسط چیست و با فرمول محاسبه و یکای آن آشنا شدیم. به نسبت مسافت طی شده به مدت زمان لازم برای طی کردن آن مسافت، تندی متوسط می‌گوییم. در حل بسیاری از مسائل مربوط به حرکت، باید با تفاوت سرعت و تندی آشنا باشیم. تندی کمیتی نرده‌ای، اما سرعت کمیتی برداری است. در فیزیک نهم با مفهوم تندی متوسط و تفاوت آن با سرعت متوسط آشنا می‌شوید، همچنین، در فیزیک دوازدهم این دو کمیت را به جزییات بیشتری یاد می‌گیرید و با حل مسائل پیچیده‌تری آشنا می‌شوید.

در نگاه نخست، تندی متوسط مفهوم بسیار ساده‌ای به نظر می‌رسد. اما مسائل مطرح شده در رابطه با آن می‌توانند بسیار پیچیده باشند. در نتیجه، درک عمیق این کمیت و تفاوت آن با سرعت، برای حل مسائل مربوط به حرکت بسیار مهم است. تماشای فیلم‌های آموزشی، مانند فیلم‌های آموزشی تهیه شده در فرادرس، می‌تواند به شما برای درک بهتر این کمیت‌ها و مسائل مربوط به آن‌ها کمک زیادی کند.

• فیلم آموزش علوم تجربی پایه نهم بخش فیزیک فرادرس
• فیلم آموزش فیزیک - پایه دوازدهم فراردس
• فیلم آموزش فیزیک ۳ - پایه دوازدهم رشته ریاضی و فیزیک - مرور و حل تمرین فرادرس
• فیلم آموزش فیزیک پایه ۱ فراردس
• فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله فراردس
• فیلم آموزش فیزیک ۱ - مرور و حل تست فرادرس

در این فیلم‌های آموزشی فرادرس:

• مفاهیمی مانند تندی، سرعت، مسافت، جابجایی، شتاب، سرعت و شتاب متوسط را به طور کامل می‌آموزید.
• نحوه حل مسائل مربوط به تندی متوسط را به صورت گام‌به‌گام فرا می‌گیرید.
• توانایی شما در تحلیل و بررسی حرکت اجسام ارتقا می‌یابد.

حل مثال و تمرین از تندی متوسط

همان‌طور که می‌دانیم تندی متوسط از تقسیم مسافت طی شده در زمان t به‌دست می‌آید. برای حل مسائل مربوط به تندی متوسط، گام‌های زیر را به ترتیب طی می‌کنیم:

• مسافتِ کلِ طی شده توسط جسم را به‌دست آورید. اگر مسیر طی شده توسط جسم به دو یا بیشتر از دو مرحله تقسیم شده باشد و جسم در هر مرحله با تندی متفاوتی حرکت کند، مسافت‌های طی شده در هر مرحله را با استفاده از رابطه $$Distance = Speed \ \times \ time$$ به‌دست آورید.
• زمان صرف شده برای پیمودن مسافتِ کل را محاسبه کنید.
• با تقسیم مسافت کل به زمانِ کل، تندی متوسط به‌دست می‌آید. یکای تندی متوسط را با توجه به یکاهای داده شده برای مسافت و زمان در کنار آن بنویسید. به عنوان مثال، اگر مسافت داده شده برحسب کیلومتر و زمان برحسب ساعت داده شده باشند، یکای تندی متوسط به صورت کیلومتر بر ساعت بیان می‌شود.

برای آشنایی بیشتر با چگونگی حل مسائل مربوط به تندی متوسط، چند مثال را قدم به قدم با یکدیگر حل می‌کنیم.

مثال ۱

فرض کنید با تندی $$x$$ کیلومتر بر ساعت از نقطه A به B و با تندی y کیلومتر بر ساعت از B به A برمی‌گردید. اگر فاصله نقطه A از B برابر d باشد، تندی متوسط چه مقدار است؟

پاسخ

تندی متوسط از تقسیم مسافت طی شده در بازه زمانی لازم برای طی کردن آن مسافت به‌دست می‌آید.

$$\overline { s } = \frac { total \enspace distance} { total \enspace time}$$

فرض کنید در مدت زمان $$t_1$$ از A به B و در مدت زمان $$t_2$$ از ‌‌B به A رفته‌اید. توجه به این نکته مهم است که مسافت طی شده در هر مرحله برابر d است، اما زمانِ رفت از A به B با زمان برگشت از B به A به دلیل حرکت با تندی‌های متفاوت، با یکدیگر برابر نیستند. رابطه تندی متوسط را می‌توانیم به صورت زیر بنویسیم:

$$\overline { s } = \frac { d + d } { t_1 + t_ 2 }$$

$$t_ 1$$ زمان رفت از A به B را به صورت زیر محاسبه می‌کنیم:

$$\overline { s } _ { A \ to \ B }= \frac { distance } { t _ 1 } \\ x = \frac { d } { t _ 1 } \\ t_ 1 = \frac { d } { x }$$

$$t_ 2$$ زمان برگشت از B ‌به A را به صورت زیر به‌دست می‌آوریم:

$$\overline { s } _ { B \ to \ A }= \frac { distance } { t _ 2 } \\ y = \frac { d } { t _ 1 } \\ t_ 1 = \frac { d } { y }$$

بنابراین، مدت زمان کل رفت و برگشت برابر است با:

$$t_ 1 + t_ 2 = \frac { d } { x } + \frac { d } { y } = \frac { d ( x + y ) } { x y }$$

با تقسیم کلِ مسافت طی شده بر مدت زمانِ صرف شده برای طی مسافت، تندی متوسط را به‌دست می‌آوریم:

$$\overline { s } = \frac { 2 d } { \frac { d ( x + y) } { x y } } \\ \overline { s } = \frac { 2 x y } { x + y }$$

مثال ۲

فرض کنید با تندی ۱۰ متر بر ثانیه از نقطه A به B و با تندی ۵ متر بر ثانیه از B به C می‌روید. اگر فاصله نقطه A تا B برابر d و فاصله نقطه B تا C برابر $$2d$$ باشد، تندی متوسط در کل مسیر چه مقدار است؟

پاسخ

این مثال نیز مشابه مثال یک است، با این تفاوت که مسیرهای پیموده شده در دو مرحله با یکدیگر تفاوت دارند. تندی متوسط با استفاده از رابطه زیر به‌دست می‌آید:

$$\overline { s } = \frac { total \enspace distance} { total \enspace time}$$

فرض کنید در مدت زمان $$t_1$$ از A به B و در مدت زمان $$t_2$$ از ‌‌B به C رفته‌اید. توجه به این نکته مهم است که مسافت طی شده در مرحله اول برابر d و در مرحله دوم برابر $$2d$$ است. رابطه تندی متوسط را می‌توانیم به صورت زیر بنویسیم:

$$\overline { s } = \frac { d + 2d } { t_1 + t_ 2 }$$

$$t_ 1$$ زمان رفت از A به B برابر است با:

$$\overline { s } _ { A \ to \ B }= \frac { distance } { t _ 1 } \\ x = \frac { d } { t _ 1 } \\ t_ 1 = \frac { d } { 10 }$$

$$t_ 2$$ زمان رفت از B ‌به C نیز برابر است با:

$$\overline { s } _ { B \ to \ A }= \frac { distance } { t _ 2 } \\ y = \frac { 2d } { t _ 1 } \\ t_ 1 = \frac { 2d } { 5 }$$

بنابراین، مدت زمان کل رفت و برگشت برابر است با:

$$t_ 1 + t_ 2 = \frac { d } { 10 } + \frac { 2d } { 5 } = \frac { d + 4 d } { 10 } = \frac { 5 d } { 10 } = \frac { d } { 2 }$$

با تقسیم کلِ مسافت طی شده بر مدت زمانِ صرف شده برای طی مسافت، تندی متوسط را به‌دست می‌آوریم:

$$\overline { s } = \frac { 3 d } { \frac { d } { 2 } } \\ \overline { s } = 6 \ \frac { m } { s }$$

مثال ۳

اتوبوسی مسیرِ بین دو شهر را در مدت زمان پنج ساعت طی می‌کند. این اتوبوس در سه ساعت اول حرکت با تندی ۸۰ کیلومتر بر ساعت و در دو ساعت پایانی حرکت، با تندی ۹۵ کیلومتر بر ساعت حرکت می‌کند. تندی متوسط چه مقدار است؟

پاسخ

تندی متوسط با استفاده از رابطه زیر به‌دست می‌آید:

$$\overline { s } = \frac { total \enspace distance} { total \enspace time}$$

رابطه فوق را برحسب مسافت به صورت زیر مرتب می‌کنیم:

$$total \enspace distance = speed \ \times \ time$$

اتوبوس به مدت سه ساعت با سرعت ۸۰ کیلومتر بر ساعت حرکت می‌کند. مسافت طی شده در این بازه زمانی برابر است با:

$$D_1 = 80 \times 3 = 240 \ km$$

در ادامه، اتوبوس به مدت دو ساعت با سرعت ۹۵ کیلومتر بر ساعت حرکت می‌کند. مسافت طی شده در این مدت برابر است با:

$$D_2 = 95 \times 2 = 190 \ km$$

بنابراین، مسافت کل طی شده توسط اتوبوس برابر است با:

$$D = total \enspace distance = D_1 + D_2 = 240 + 190 = 430 \ km$$

مدت زمان حرکت بین دو شهر برابر ۵ ساعت است. در نتیجه، تندی متوسط برابر است با:

$$\overline { s } = \frac { 430 \ km } { 5 \ h } \\ \overline { s } = 86 \ \frac { km } { h }$$

مثال ۴

راننده‌ای با تندی ۲۴ مایل بر ساعت به مدت ۲ ساعت حرکت می‌کند. سپس، به دلیل ترافیک، سرعت خود را به ۱۸ مایل بر ساعت کاهش می‌دهد و پس از ۲ ساعت به مقصد می‌رسد. تندی متوسط برحسب کیلومتر بر ساعت چه مقدار است؟ (هر مایل در حدود ۱٫۶۱ کیلومتر است)

پاسخ

تندی متوسط با استفاده از رابطه زیر به‌دست می‌آید:

$$\overline { s } = \frac { total \enspace distance} { total \enspace time}$$

رابطه فوق را برحسب مسافت به صورت زیر مرتب می‌کنیم:

$$total \enspace distance = speed \ \times \ time$$

همان‌طور که مشاهده می‌کنید تندی برحسب مایل بر ساعت داده شده است،‌ اما تندی متوسط را باید برحسب کیلومتر بر ساعت به‌دست آوریم. برای این کار، تندی‌های داده شده را به کیلومتر بر ساعت تبدیل می‌کنیم. برای تبدیل مایل بر ساعت به کیلومتر بر ساعت، تنها کافی است تندی داده شده برحسب مایل بر ساعت را در ۱٫۶۱ ضرب کنیم:

$$24 \ \frac { mile } { h } = 24 \times 1.61 \ \frac { km } { h } = 38.64 \ \frac { km} { h } \\ 18 \ \frac { mile } { h } = 18 \times 1.6 \ \frac { km } { h } = 28.98 \ \frac { km } { h }$$

راننده ابتدا با تندی ۳۸٫۶۴ کیلومتر بر ساعت به مدت دو ساعت حرکت می‌کند. مسافت طی شده در این مدت برابر است با:

$$D_1 = 38.64 \times 2 = 77.28 \ km$$

در ادامه، راننده به مدت دو ساعت با سرعت ۲۸٫۹۸ کیلومتر بر ساعت حرکت می‌کند و پس از دو ساعت به مقصد می‌رسد. مسافت طی شده در این مدت برابر است با:

$$D_2 = 28.98 \times 2 = 57.96 \ km$$

بنابراین، مسافت کل طی شده توسط راننده برابر است با:

$$D = total \enspace distance = D_1 + D_2 = 77.28+57.96 = 135.24 \ km$$

مدت زمان حرکت بین دو شهر برابر ۴ ساعت است. در نتیجه، با قرار دادن مقدارهای مسافت و زمان در رابطه تندی متوسط، مقدار آن را به‌دست می‌آوریم:

$$\overline { s } = \frac { 135.24 \ km } { 5 \ h } \\ \overline { s } = 33.81 \ \frac { km } { h }$$

مقایسه سرعت متوسط و تندی متوسط

در مطلب «سرعت متوسط چیست ؟ – فرمول، تعریف و محاسبه + حل تمرین» از مجله فرادرس با تعریف سرعت متوسط آشنا شدیم. همچنین، تا اینجا فهمیدیم تندی متوسط چیست و چه تفاوتی با سرعت متوسط دارد. تندی متوسط از تقسیم مسافت کل بر زمان صرف شده برای طی کردن مسافت به ‌دست می‌آید. در مقابل، برای محاسبه سرعت متوسط باید جابجایی را بر زمان لازم برای انجام جابجایی تقسیم کنیم. همچنین، سرعت متوسط کمیتی برداری است و اندازه و جهت دارد، اما تندی متوسط کمیتی نرده‌ای و تنها دارای اندازه است. توجه به این نکته نیز مهم است که سرعت متوسط می‌تواند منفی یا مثبت باشد، اما تندی متوسط تنها مقدارهای مثبت را می‌پذیرد. در این بخش، چند مثال در رابطه با تندی و سرعت متوسط حل و این دو کمیت را با یکدیگر مقایسه می‌کنیم.

مثال ۱

مردی برای رفتن به فروشگاهی در شرق خانه خود، ابتدا به مدت دو ساعت، ۷ کیلومتر به سمت شرق، سپس به مدت یک ساعت، ۲ کیلومتر در همان جهت حرکت می‌کند. تندی متوسط و سرعت متوسط مرد چه مقدار است؟

پاسخ

تصویر زیر، مسیر حرکت مرد را نشان می‌دهد. A نقطه آغاز حرکت و C نقطه پایان حرکت است:

ابتدا تندی متوسط را به‌دست می‌آوریم. برای به‌دست آوردن تندی متوسط باید مسافتِ کلِ طی شده توسط مرد را محاسبه کنیم. مسافت به کل مسیر طی شده توسط مرد بستگی دارد. شخص روی خطی افقی، ۹ کیلومتر به سمت شرق رفته است. در نتیجه، مقدار تندی متوسط او برابر است با:

$$\overline { v } = \frac { distance } { total \ time } \\ \overline { v } = \frac { 9 \ km } { 2 \ h + 1 \ h } = \frac { 9 \ km } { 3 \ h } = 3 \ \frac { km } { h }$$

برای به‌دست آوردن سرعت متوسط باید جابجایی کلِ طی شده توسط مرد را محاسبه کنیم. جابجایی به نقطه ابتدا (نقطه A)‌ و انتهای مسیر (‌نقطه C) بستگی دارد و مستقل از مسیر پیموده شده است. فاصله نقطه A و C برابر ۹ کیلومتر است. در نتیجه، مقدار سرعت متوسط برابر است با:

$$\overline { v } = \frac { displacement } { total \ time } \\ \overline { v } = \frac { 9 \ km } { 2 \ h + 1 \ h } = \frac { 9 \ km } { 3 \ h } = 3 \ \frac { km } { h }$$

همان‌طور که مشاهده می‌کنید، سرعت متوسط و تندی متوسط با یکدیگر برابر هستند. اما همیشه این‌گونه نیست. در این مثال، مرد روی خطی مستقیم و بدون تغییر جهت، مسیری را پیموده است.

مثال ۲

سارا پیاده‌روی را به عنوان ورزش صبحگاهی انتخاب کرده است. او هر روز صبح مسیر مشخصی را طی می‌کند. ابتدا، ۷ کیلومتر به مدت دو ساعت به سمت شرق، سپس ۲٫۵ کیلومتر به مدت یک ساعت به سمت غرب می‌رود. تندی و سرعت متوسط او چه مقدار است؟

پاسخ

تصویر زیر، مسیر پیاده‌روی سارا را نشان می‌دهد. A نقطه آغاز حرکت و D نقطه پایان حرکت است:

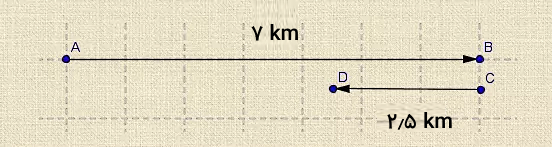
ابتدا تندی متوسط را به‌دست می‌آوریم. برای به‌دست آوردن تندی متوسط، مسافتِ کلِ طی شده توسط سارا را محاسبه می‌کنیم. سارا روی خطی افقی، ۹ کیلومتر به سمت شرق رفته و ۲٫۵ کیلومتر به سمت غرب برگشته است. در نتیجه، مقدار تندی متوسط او برابر است با:

$$\overline { s } = \frac { distance } { total \ time } \\ \overline { s } = \frac { 7 \ km + 2.5 \ km } { 2 \ h + 1 \ h } = \frac { 9.5 \ km } { 3 \ h } = 3.2 \ \frac { km } { h }$$

برای به‌دست آوردن سرعت متوسط باید جابجایی کلِ طی شده توسط سارا را محاسبه کنیم. جابجایی به نقطه ابتدا (نقطه A)‌ و انتهای مسیر (‌نقطه D) بستگی دارد. فاصله نقطه A و D برابر ۵٫۵ کیلومتر است. در نتیجه، مقدار سرعت متوسط برابر است با:

$$\overline { v } = \frac { displacement } { total \ time } \\ \overline { v } = \frac { 4.5 \ km } { 2 \ h + 1 \ h } = \frac { 4.5 \ km } { 3 \ h } = 1.5 \ \frac { km } { h }$$

همان‌طور که مشاهده می‌کنید، سرعت متوسط و تندی متوسط با یکدیگر برابر نیستند. در این مثال، سارا مسیر خود را به هنگام پیاده‌روی تغییر داده است.

مثال ۳

پارکی به شکل دایره‌ای با شعاع ۰٫۵ کیلومتر، نزدیک خانه سیما قرار دارد. سیما تصمیم می‌گیرد پس از مدت‌ها برای پیاده‌روی به این پارک برود و یک بار آن را دور بزند. او از نقطه A شروع به حرکت می‌کند و پس از یک ساعت دوباره به این نقطه می‌رسد. مقدار سرعت و تندی متوسط سیما چه مقدار است؟

پاسخ

ابتدا تندی متوسط را به‌دست می‌آوریم. برای به‌دست آوردن تندی متوسط باید مسافت کل طی شده توسط سیما را محاسبه کنیم. او روی مسیری به شکل دایره، یک دور کامل می‌زند. بنابراین، کلِ مسافت طی شده توسط سیما برابر محیط دایره است و به صورت زیر به‌دست می‌آید:

$$D = 2 \pi r = 2 \times \pi \times 0.5 = 3.14 \ km$$

سیما در مدت زمان یک ساعت، پارک را دور زده است. در نتیجه، تندی متوسط او برابر است با:

$$\overline { s } = \frac { distance } { total \ time } \\ \overline { s } = \frac { 3.14 \ km } { 1 \ h } = 3.14 \ \frac { km } { h }$$

برای به‌دست آوردن سرعت متوسط باید جابجایی کلِ سیما را به‌دست آوریم. همان‌طور که می‌دانیم جابجایی به نقطه ابتدا (نقطه A)‌ و انتهای مسیر (‌نقطه A) بستگی دارد. با توجه به یکسان بودن نقطه ابتدا و انتهای مسیر، جابجایی کل و در نتیجه، سرعت متوسط برابر صفر هستند.

نکته: در حرکت‌های رفت و برگشتی و حرکت روی مسیری به شکل دایره، تندی متوسط و سرعت متوسط با یکدیگر برابر نیستند.

مثال ۴

سحر تصمیم می‌گیرد برای دیدن مادربزرگ به روستای محل زندگی او برود. او صبحِ زود از خانه خارج می‌شود و برای رفتن به روستا، ابتدا با سرعت ۶۰ کیلومتر بر ساعت، ۱۲۰ کیلومتر به سمت جنوب، سپس با سرعت ۵۰ کیلومتر بر ساعت، ۱۵۰ کیلومتر به سمت شرق رانندگی می‌کند. مقدار سرعت و تندی متوسط سیما چه مقدار است؟

پاسخ

تصویر زیر، مسیر رانندگی سحر را نشان می‌دهد. A نقطه آغاز حرکت و C نقطه پایان حرکت است:

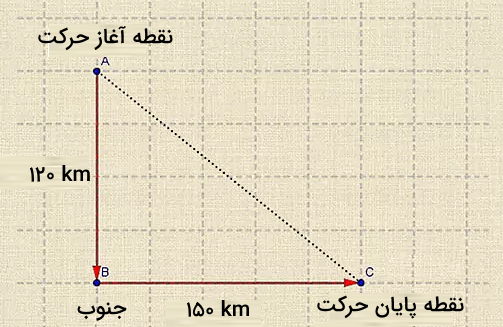
برای به‌دست آوردن تندی متوسط، ابتدا مسافت کل طی شده توسط سحر را محاسبه کنیم. سحر ۱۲۰ کیلومتر به سمت جنوب، سپس ۱۵۰ کیلومتر به سمت شرق رانندگی می‌کند. از آنجا که مسافت به شکلِ مسیر طی شده بستگی دارد، مقدار آن برابر است با:

$$D = 120 \ km + 150 \ km = 270 \ km$$

در ادامه، زمان کل را به‌دست می‌آوریم. سحر با تندی ۶۰ کیلومتر بر ساعت، ۱۲۰ کیلومتر به سمت جنوب رانندگی می‌کند. مدت زمان لازم برای طی کردن این مسافت برابر است با:

$$t_1 = \frac { 120 } { 60 } = 2 \ h$$

سحر، سپس با تندی ۵۰ کیلومتر بر ساعت، ۱۵۰ کیلومتر به سمت شرق رانندگی می‌کند. مدت زمان لازم برای طی کردن این مسافت برابر است با:

$$t_1 = \frac { 150 } { 50 } = 3 \ h$$

با داشتن زمان و مسافت کل، تندی متوسط را به‌دست می‌آوریم:

$$\overline { s } = \frac { distance } { total \ time } \\ \overline { s } = \frac { 270 \ km } { 5 \ h } = 54 \ \frac { km } { h }$$

برای به‌دست آوردن سرعت متوسط باید جابجایی کلِ سیما را به‌دست آوریم. جابجایی خط‌چینِ سیاه نشان داده شده در تصویر بالا یا وتر مثلث ABC است:

$$AC ^ 2 = AB^ 2 + BC ^ 2 \\ AC = \sqrt { AB^ 2 + BC ^ 2 } = \sqrt { ( 120 ) ^ 2 + ( 150 ^ 2 ) } = 192.1 \ km$$

با قرار دادن جابجایی و زمان کل در رابطه سرعت متوسط، مقدار آن را به‌دست می‌آوریم:

$$\overline { v } = \frac { displacement } { total \ time } \\ \overline { v } = \frac { 191.1 \ km } { 5 \ h } = 38 . 4 \ \frac { km } { h }$$

محاسبه تندی متوسط از روی نمودار مکان زمان

تا اینجا می‌دانیم تندی متوسط چیست و با استفاده از چه رابطه‌ای به‌دست می‌آید. همچنین، با تفاوت تندی متوسط و سرعت متوسط آشنا شدیم. تندی متوسط را با استفاده از نمودار مکان زمان نیز می‌توانیم به‌دست آوریم. برای آشنایی با چگونگی محاسبه تندی متوسط با استفاده از نمودار مکان زمان، ابتدا این نمودار و مشخصات آن را به اختصار توضیح می‌دهیم.

نمودار مکان زمان چیست؟

به کمک نمودار مکان زمان، اطلاعات بسیار مهمی را در مورد حرکت اجسام مختلف به‌دست می‌آوریم. محور عمودی در نمودار مکان زمان، مکانِ جسم را نسبت به مبدا و محور افقی، زمان را نشان می‌دهد. این نمودار اطلاعاتی در مورد مسافت، جابجایی، سرعت، تندی و شتاب جسم به ما می‌دهد. به عنوان مثال، شیب خط مماس بر نمودار مکان زمان، بیان‌گر سرعت حرکت جسم است. بنابراین، مقدار شیب خط مماس بر نمودار مکان زمان در هر لحظه از زمان، سرعت جسم را در آن لحظه به می‌دهد.

جابجایی و مسافت در نمودار مکان زمان

در بخش‌های قبل با تفاوت مسافت و جابجایی آشنا شدیم. مسافت، کمیتی نرده‌ای و برابر طول مسیر طی شده توسط جسم و به شکل مسیر، وابسته است. در مقابل، جابجایی کمیتی برداری است که به صورت کوتاه‌ترین مسیر بین دو نقطه (نقطه آغاز و پایان)، تعریف می‌شود. در نتیجه، جابجایی، برخلاف مسافت، تنها به نقاط ابتدا و انتهای مسیر بستگی دارد. تفاوت مهم دیگر بین مسافت و جابجایی آن است که مسافت طی شده توسط جسم همواره مثبت است. در حالی‌که، جابجایی ممکن است مثبت یا منفی باشد. برای به‌دست آوردن جابجایی در بازه زمانی مشخص از روی نمودار مکان زمان، به مکان جسم در نقطه ابتدا و انتهای بازه زمانی توجه می‌کنیم. اما برای محاسبه مسافت طی شده توسط جسم از روی نمودار مکان زمان، باید به کل مسیر طی شده توسط جسم دقت کنیم.

در ادامه، با حل چند مثال، چگونگی محاسبه تندی متوسط با استفاده از نمودار مکان زمان را با یکدیگر بررسی می‌کنیم.

چگونه تندی متوسط را از روی نمودار مکان زمان به دست آوریم؟

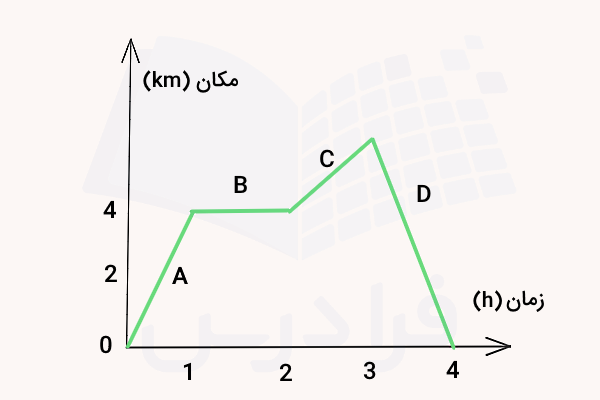
نمودار مکان زمان جسمی در تصویر زیر نشان داده شده است. با توجه به نمودار به هر یک از پرسش‌های مطرح شده در ادامه پاسخ دهید.

پرسش ۱

تندی متوسط جسم در مسیر A چه مقدار است؟

پاسخ

برای محاسبه تندی متوسط جسم در مسیر A باید مسافت و زمان کل را برای این مسیر به‌دست آوریم. همچنین، جسم در زمان صفر در مبدا و پس از یک ساعت در ۴ کیلومتری مبدا قرار دارد. بنابراین، جسم در مسیر A مسافتی برابر ۴ کیلومتر را طی کرده است. با داشتن مسافت و زمان، به راحتی می‌توانیم تندی متوسط را به‌دست آوریم:

$$\overline { s } _ A= \frac { distance } { total \ time } \\ \overline { s } = \frac { 4 \ km } { 1 \ h } = 4 \ \frac { km } { h }$$

پرسش ۲

تندی متوسط جسم در مسیر B چه مقدار است؟

پاسخ

به نمودار مکان زمان در قسمت ‌‌‌B دقت کنید. نمودار در این قسمت خطی افقی با شیبِ صفر است. خط افقی در نمودار مکان زمان، جسم ساکن را نشان می‌دهد. در نتیجه، جسم پس از قرار گرفتن در فاصله ۴ کیلومتری از مبدا، به مدت یک ساعت در آنجا ساکن می‌ماند. از این‌رو، مسافت طی شده توسط جسم و تندی متوسط آن برابر صفر است.

پرسش ۳

تندی متوسط جسم در مسیر C چه مقدار است؟

پاسخ

جسم پس از یک ساعت توقف، شروع به حرکت می‌کند و پس از یک ساعت به ۶ کیلومتری مبدا می‌رسد . بنابراین، جسم در مسیر C مسافتی برابر ۲ کیلومتر را طی کرده است. با داشتن مسافت و زمان، به راحتی می‌توانیم تندی متوسط را به‌دست آوریم:

$$\overline { s } _ C = \frac { distance } { total \ time } \\ \overline { s } = \frac { 2 \ km } { 1 \ h } = 2 \ \frac { km } { h }$$

پرسش ۴

تندی متوسط جسم در مسیر D چه مقدار است؟

پاسخ

جسم ۳ ساعت پس از شروع حرکت و قرار گرفتن در فاصله ۶ کیلومتری از مبدا، با تغییر مسیر به سمت مبدا شروع به حرکت می‌کند و یک ساعت بعد به آن می‌رسد. بنابراین، جسم در مسیر D مسافتی برابر ۶ کیلومتر را طی کرده است. با داشتن مسافت و زمان، به راحتی می‌توانیم تندی متوسط را به‌دست آوریم:

$$\overline { s } _ C = \frac { distance } { total \ time } \\ \overline { s } = \frac { 6 \ km} { 1 \ h } = 6 \ \frac { km } { h }$$

پرسش ۵

تندی متوسط در کل مسیر چه مقدار است؟

پاسخ

همان‌طور که در نمودار فوق مشاهده می‌کنید، جسم ۶ ساعت پس از شروع حرکت به مبدا برمی‌گردد. آیا مسافت کل برابر صفر است؟ خیر، جابجایی کل برابر صفر، اما مسافت کل برابر ۱۲ کیلومتر است. با توجه به آن‌که زمان کل حرکت برابر ۴ ساعت است، تندی متوسط حرکت برابر ۳ کیلومتر بر ساعت به‌دست می‌آید.

در این بخش فهمیدیم چگونه تندی متوسط را از روی نمودار مکان زمان به‌دست آوریم. در ادامه، چند مثال در این رابطه را با یکدیگر حل می‌کنیم.

مثال ۱

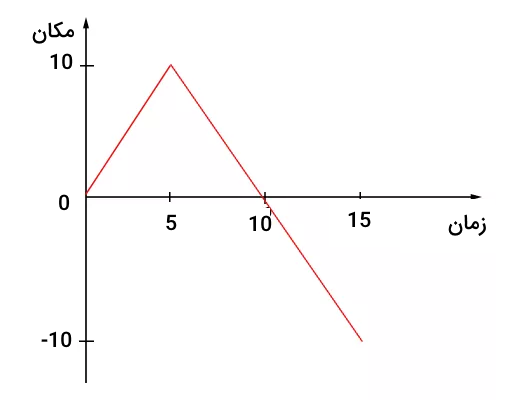
جسمی روی مسیری افقی و مستقیم حرکت می‌کند. نمودار مکان زمان آن در تصویر زیر نشان داده شده است. تندی متوسط جسم را در فاصله زمانی صفر تا ۱۵ ثانیه به دست آورید.

پاسخ

برای محاسبه تندی متوسط جسم بین زمان صفر تا ۱۵ ثانیه باید مسافت کل را برای این مدت زمان به‌دست آوریم. حرکت جسم در ۱۵ ثانیه به صورت زیر توصیف می‌شود:

• جسم در زمان صفر در مبدا و ۵ ثانیه پس از شروع حرکت به ۱۰ متری مبدا می‌رسد.
• در ادامه، جسم تغییر مسیر می‌دهد و به سمت مبدا حرکت می‌کند و ۵ ثانیه بعد به مبدا می‌رسد.
• جسم با رسیدن به مبدا متوقف نمی‌شود، بلکه به حرکت خود در جهت مخالف ادامه می‌دهد و ۱۵ ثانیه پس از شروع حرکت به ۱۰ متری مبدا (در جهت مخالف) می‌رسد.

برای درک بهتر حرکت جسم، مسیر حرکت آن را روی خط افقی به صورت زیر رسم می‌کنیم.

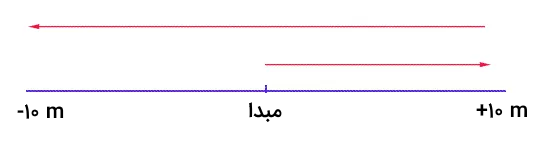
به یاد داشته باشید که مسافت، کمیتی نرده‌ای است و به مسیر طی شده توسط جسم بستگی دارد. بنابراین، مسافت طی شده توسط جسم را در هر مرحله با یکدیگر جمع و مسافتِ کل را به‌دست می‌آوریم:

$$D = 10 + 20= 30 \ m$$

با قرار دادن مسافت و زمانِ کل در رابطه تندی متوسط، مقدار آن به صورت زیر به‌دست می‌آید:

$$\overline { s } = \frac { distance } { total \ time } \\ \overline { s } = \frac { 30 \ m } { 15 \ s } =2 \ \frac { m } { s }$$

پرسش: سرعت متوسط در کلِ مسیر چه مقدار است؟

پاسخ: سرعت متوسط از تقسیم جابجایی کل بر مدت زمان کل به‌دست می‌آید. بنابراین، برای محاسبه سرعت متوسط در کلِ مسیر، باید جابجایی جسم را به‌دست آوریم. جابجایی، کمیتی برداری است و با استفاده از رابطه زیر به‌دست می‌آید:

$$\triangle \overrightarrow{ x } = x_f - x_ i$$

در رابطه فوق،‌ $$x_i$$ مکان جسم در ابتدا و $$x_f$$ مکان جسم در انتهای حرکت است. بر طبق تصویر فوق، جسم در زمان صفر در مکان صفر و ۱۵ ثانیه پس از شروع حرکت در مکان ۱۰- متری مبدا قرار دارد. در نتیجه، جابجایی کل برابر است با:

$$\triangle \overrightarrow{ x } = -10 - 0 = - 10 \ m$$

با قرار دادن زمان و جابجایی کل در رابطه سرعت متوسط، مقدار آن را به‌دست می‌آوریم:

$$\overrightarrow{\overline{ v } } = \frac { \triangle { \overrightarrow{ x }}} { \triangle t } = \frac { -10 \ m } { 15 } =- \ \frac { 2 } { 3 } \ \frac { m } { s }$$

مثال ۲

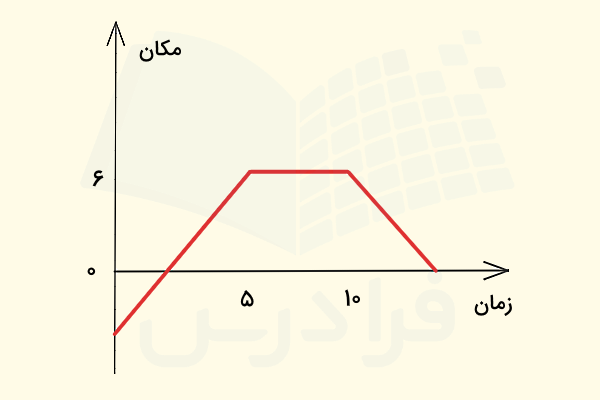
نمودار مکان زمان جسمی به صورت نشان داده شده در تصویر زیر است. اگر تندی متوسط در ۱۰ ثانیه اولیه حرکت برابر ۱٫۶ متر بر ثانیه باشد، در چه لحظه‌ای جهت بردار مکان جسم تغییر می‌کند؟

پاسخ

در این مثال باید با داشتن مقدار تندی متوسط جسم در ۱۰ ثانیه اول حرکت، زمانی که بردار مکان جسم، تغییر جهت می‌دهد را به‌دست آوریم. تندی متوسط در ۱۰ ثانیه اولیه حرکت برابر ۱٫۶ متر بر ثانیه است، با توجه به فرمول تندی متوسط، به راحتی می‌توانیم، مسافت کل پیموده شده توسط جسم در این مدت زمان را محاسبه کنیم:

$$\overline { s } = \frac { distance } { total \ time } \\ 1.6 = \frac { distance } { 10 \ s } \\ D= 16 \ m$$

در ادامه، مکان جسم در زمان صفر یا مکان اولیه جسم را به‌دست می‌آوریم. برای انجام این کار از مسافت کلِ به‌دست آمده استفاده می‌کنیم:

$$( 6 - x_ 0 ) + 6 = 16 \\ 12 - x_ 0 = 16 \\ -x_0 = 4 \\ x_ 0 = - \ 4 \ m$$

بنابراین، جسم در زمانِ صفر در مکان ۴- متر قرار دارد. سپس، به سمت مبدا شروع به حرکت می‌کند و در زمان t به آن می‌رسد. توجه به این نکته مهم است که جهت بردارِ مکانِ جسم با عبور از مبدا، تغییر می‌کند. برای به‌دست آوردن زمان عبور جسم از مبدا، تنها کافی است معادله مکان برحسب زمانِ جسم را در ۵ ثانیه اول حرکت بنویسیم و مقدار مکان را برابر صفر قرار دهیم. معادله مکان برحسب زمان جسم به صورت زیر نوشته می‌شود:

$$x = x_0 + vt$$

سوالی که ممکن است مطرح شود آن است که چرا معادله مکان برحسب زمان به صورت $$x = x_0 + vt$$ نوشته شده است. از آنجا که نمودار مکان زمانِ جسم به صورت خطی مستقیم با شیب ثابت و مثبت است، جسم در ۵ ثانیه اول حرکت به صورت یکنواخت و با سرعت ثابت حرکت می‌کند. برای نوشتن معادله مکان برحسب زمان در حرکت یکنواخت، باید سرعت اولیه و سرعت حرکت جسم را بدانیم. سرعت اولیه را به‌دست آوردیم. برای محاسبه سرعت حرکت، تنها کافی است شیب خط نمودار مکان زمان را به‌دست آوریم.

$$slope = v = \frac { x_2 - x_ 1 } { t _ 2 - t _ 1 } = \frac { 6 - ( - 4 ) } { 5 - 0 } = 2 \ \frac { m } { s }$$

با داشتن سرعت و مکان اولیه، معادله مکان زمان را می‌توانیم به صورت زیر بنویسیم:

$$x = 2t - 4$$

برای به‌دست آوردن زمانِ تغییر جهت مکانِ جسم، مقدار $$x$$ را برابر صفر قرار می‌دهیم:

$$0 = 2 t - 4 \\t = 2 \ s$$

مثال ۳

نمودار مکان زمان جسمی به صورت نشان داده شده در تصویر زیر است. اگر تندی متوسط در ۵ ثانیه اولیه حرکت برابر ۲۰ متر بر ثانیه باشد، جسم با چه سرعتی و در چه زمانی از مبدا مکان عبور می‌کند؟

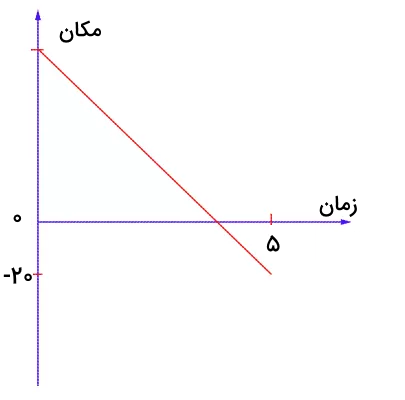
پاسخ

در این مثال باید زمان عبور جسم از مبدا و سرعت آن به هنگام عبور از مبدا را به‌دست آوریم. برای حل آن، گام‌های زیر را به‌ ترتیب طی می‌کنیم.

• گام اول

باید معادله مکان برحسب زمان را برای جسم به‌دست آوریم. معادله مکان برحسب زمان جسم به صورت زیر نوشته می‌شود:

$$x = x_0 + vt$$

معادله فوق، معادله حرکت یکنواخت است، زیرا جسم در ۵ ثانیه اول حرکت به صورت یکنواخت و با سرعت ثابت حرکت می‌کند. برای نوشتن این معادله باید مکان اولیه و سرعت حرکت جسم را به‌دست آوریم.

• گام دوم

تندی متوسط در ۵ ثانیه اولیه حرکت برابر ۲۰ متر بر ثانیه است، با توجه به فرمول تندی متوسط، به راحتی می‌توانیم، مسافت کل پیموده شده توسط جسم در این مدت زمان را محاسبه کنیم:

$$\overline { s } = \frac { distance } { total \ time } \\ 20 = \frac { distance } { 5 \ s } \\ D= 100 \ m$$

در ادامه، مکان جسم در زمان صفر یا مکان اولیه جسم را به‌دست می‌آوریم. برای انجام این کار از مسافت کلِ به‌دست آمده استفاده می‌کنیم:

$$( x_0 - (-20) ) = 100 \\ x_ 0 +20 = 100 \\ x_ 0 = + \ 80 \ m$$

جسم در لحظه صفر در ۸۰ متری مبدا قرار دارد. جهت راست را به صورت قراردادی به صورت جهت مثبت انتخاب می‌کنیم. جسم از ۸۰ متری مبدا، در خلاف جهت مثبت، شروع به حرکت می‌کند و پس از ۵ ثانیه، به مکان ۲۰- متر می‌رسد.

• گام سوم

در این قسمت سرعت حرکت جسم را به‌دست می‌آوریم. توجه به این نکته مهم است که شیبِ نمودار مکان زمان، سرعت را به ما می‌دهد:

$$v = \overline { v } = \frac { x_ 2 - x_ 1 } { t_ 2 - t _ 1 } = \frac { -20 - 80 } { 5 } = -20 \ \frac { m } { s }$$

نکته: سرعت متوسط و سرعت لحظه‌ای در حرکت یکنواخت با یکدیگر برابر هستند.

• گام چهارم

معادله حرکت جسم به صورت زیر نوشته می‌شود:

$$x = x_ 0 + vt = -20 t + 80 \\ -20 t + 80 = 0 \\ t = 4 \ s$$

در نتیجه، جسم با سرعت ۲۰- متر بر ثانیه در زمان ۴ ثانیه از مبدا مکان عبور می‌کند.

جمع‌بندی

در این مطلب از مجله فرادرس، به پرسش تندی متوسط چیست به زبان ساده پاسخ دادیم و تفاوت آن را با سرعت متوسط بیان کردیم. همچنین، با مورد نحوه محاسبه تندی متوسط با استفاده از نمودار سرعت-زمان آشنا شدیم. در حالت کلی، تندی متوسط از تقسیم مسافت بر زمان صرف شده برای طی مسافت به‌دست می‌آید. از آنجا که مسافت کمیتی نرده‌ای است، تندی متوسط نیز کمیتی نرده‌ای خواهد بود.