تبدیل کلارک — به زبان ساده
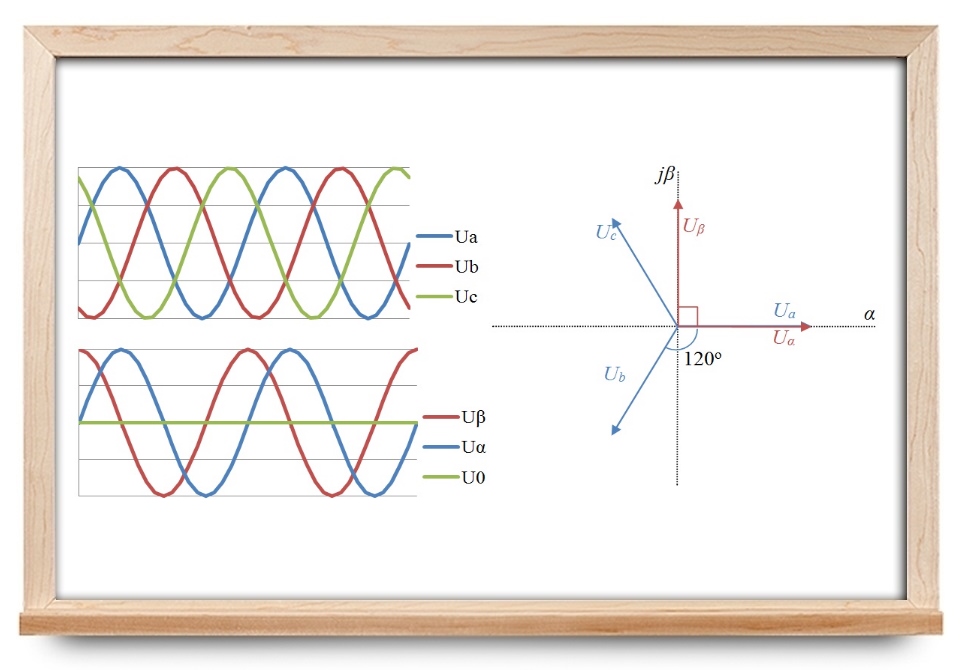
در این آموزش، تبدیلی را معرفی میکنیم که تحلیل مدارهای سهفاز را آسان میکند. «تبدیل کلارک» (Clarke Transform) یا تبدیل $$ \alpha \beta 0 $$، یک تبدیل فضای برداری سیگنالهای حوزه زمان (مثلاً ولتاژ، جریان، شار و...) از یک سیستم سهفاز (ABC) به یک قاب مرجع دوفاز ساکن ($$ \alpha \beta 0 \, $$) است. این تبدیل، بهیاد اولین زن در مهندسی برق، «ادیت کلارک» (Edith Clarke) نامگذاری شده است.
تبدیل کلارک یا $$ \Large {\alpha \beta 0}$$
فازورهای ولتاژ شکل زیر را در نظر بگیرید.
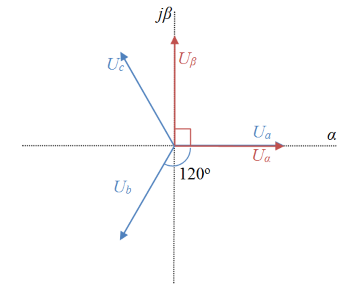
در قاب مرجع خنثی، توزیع ولتاژ سه محور ساکن $$U_a$$، $$U_b$$ و $$ U_c$$ برابر با $$ 120 ^ \circ $$ است. مختصات کارتزین نیز رسم شده که در آن، $$ U_{\alpha} $$ محور افقی در جهت فاز $$ U_ a$$، و محور عمودی بهاندازه $$ 90 ^ \circ$$ نسبت به $$ U_{\beta} $$ اختلاف فاز دارد. اندازه پریونیت بردارهای $$ U_{\alpha} $$ و $$ U_{\beta} $$ برابر است.
ولتاژهای سهفاز روی محورهای $$a$$، $$b$$ و $$c$$ با زمان تغییر میکنند و میتوان آنها را به صورت جبری به ولتاژهای دوفاز تبدیل کرد که روی محورهای $$ \alpha $$ و $$ \beta $$ با تبدیل زیر تغییر میکنند:
$$ \large T _ { \alpha \beta 0 } = \frac { 2 } { 3 } \begin {bmatrix} 1 & - \frac { 1 } { 2 } & - \frac { 1 } { 2 } \\
0 & \frac { \sqrt { 3 } } { 2 } & - \frac { \sqrt { 3 } } { 2 } \\
\frac { 1 } { 2 } & \frac { 1 } { 2} & \frac { 1 } { 2 } \\
\end{bmatrix} $$
معکوس این تبدیل را میتوان برای تبدیل مقادیر از دوفاز به سهفاز بهکار برد:
$$ \large T _ { \alpha \beta 0 } ^ { - 1 } = \begin{bmatrix} 1 & 0 & 1\\
- \frac { 1 } { 2 } & \frac { \sqrt { 3 } } { 2 } & 1 \\
- \frac { 1 } { 2 } & - \frac { \sqrt { 3 } } { 2 } & 1 \end{bmatrix} $$
لازم به ذکر است که مؤلفه صفر تبدیل کلارک، مشابه مؤلفه توالی صفر در تبدیل مؤلفههای متقارن است؛ مثلاً برای ولتاژهای $$U_a$$، $$U_b$$ و $$U_c$$ مؤلفه توالی صفر برای هردو تبدیل کلارک و مؤلفههای متقارن برابر با $$ \frac { 1 } { 3 } \left ( U _ { a } + U _ { b } + U _ { c } \right ) $$ است.
تبدیل کلارک ولتاژهای سهفاز متعادل
ولتاژهای سهفاز متعادل زیر را در نظر بگیرید:
$$ \large \begin{bmatrix} U _ { a } \\ U _ { b } \\ U _ { c } \\ \end{bmatrix} = \begin{bmatrix} U _ { m } \cos ( \omega t ) \\ U _ { m } \cos ( \omega t + \frac { 2 \pi } { 3 } ) \\ U _ { m } \cos ( \omega t - \frac{2\pi}{3}) \\ \end{bmatrix} $$
با اعمال تبدیل کلارک، داریم:
$$ \large \begin{align*}
\begin{bmatrix} U _ { \alpha } \\ U _ { \beta } \\ U _ { 0 } \\ \end{bmatrix} &= T _ { \alpha \beta 0 } \begin{bmatrix} U _ { a } \\ U _ { b } \\ U _ { c } \\ \end{bmatrix} \\
&= \frac { 2 } { 3 } \begin{bmatrix} 1 & - \frac { 1 } { 2 } & -\frac { 1 } { 2 } \\
0 & \frac { \sqrt { 3 } } { 2 } & - \frac { \sqrt { 3 } } { 2 } \\
\frac { 1 } { 2 } & \frac { 1 } { 2 } & \frac { 1 } { 2 } \\
\end{bmatrix} \begin{bmatrix} U _ { m } \cos ( \omega t ) \\ U _ { m } \cos ( \omega t + \frac { 2 \pi } { 3 } ) \\ U _ { m } \cos ( \omega t - \frac { 2 \pi } { 3 } ) \\ \end{bmatrix} \\
&= \begin{bmatrix}
\frac { 2 U _ { m } } { 3 } \left [ \cos ( \omega t ) - \frac { 1 }{ 2 } \cos ( \omega t + \frac { 2 \pi } { 3 } ) - \frac { 1 } { 2 } \cos ( \omega t - \frac { 2 \pi } { 3 } ) \right ] \\
\frac { \sqrt { 3 } U_ { m } } { 3 } \left [ \cos ( \omega t + \frac { 2 \pi } { 3 } ) - \cos ( \omega t - \frac { 2 \pi } { 3 } ) \right ] \\
\frac { U _ { m } } { 3 } \left [ \cos ( \omega t ) + \cos ( \omega t + \frac { 2 \pi } { 3 } ) + \cos ( \omega t - \frac { 2 \pi } { 3 } ) \right ] \\
\end{bmatrix} \\
&= \begin{bmatrix}
U _ { m } \cos ( \omega t ) \\
U _ { m } \sin ( \omega t ) \\
0 \\
\end{bmatrix}
\end{align*} $$
نتیجه شبیهسازی حوزه زمانِ تبدیل از دستگاه مختصات سهفاز ساکن به دوفاز ساکن، در شکلهای زیر نشان داده شده است.
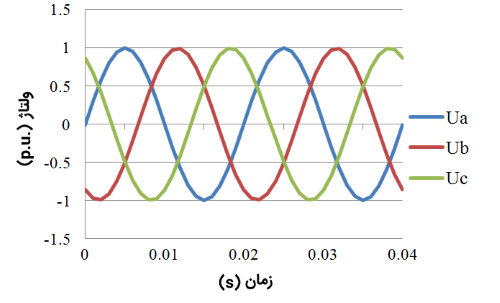
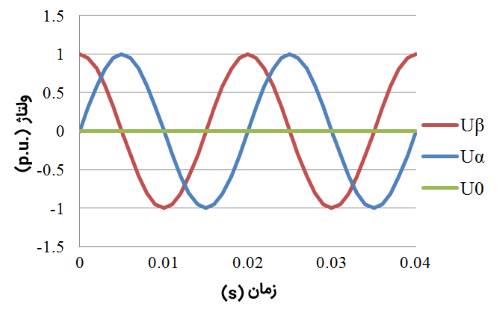
از معادلات و شکلهای بالا میتوان نتیجه گرفت که شرایط تعادل، $$ U_{\alpha} $$ و $$ U_{\beta} $$ توابعی سینوسی هستند و $$U_0$$ برابر با صفر است.
تبدیل کلارک جریانهای سهفاز متعادل
بهطریق مشابه، میتوان تبدیل کلارک جریانهای سهفاز را (که با زاویه دلخواه $$\delta $$ نسبت به ولتاژ پسفاز است) محاسبه کرد:
$$ \large \begin{bmatrix} I_{a} \\ I_{b} \\ I_{c} \\ \end{bmatrix} = \begin{bmatrix} I_{m} \cos(\omega t - \delta) \\ I_{m} \cos(\omega t - \delta + \frac{2\pi}{3}) \\ I_{m} \cos(\omega t - \delta - \frac{2\pi}{3}) \\ \end{bmatrix} $$
با روندی مشابه آنچه در قسمت قبل گفته شد، تبدیل کلارک به صورت زیر است:
$$ \large \begin{align*} \begin{bmatrix} I_{\alpha} \\ I_{\beta} \\ I_{0} \\ \end{bmatrix} &= T_{\alpha \beta 0} \begin{bmatrix} I_{a} \\ I_{b} \\ I_{c} \\ \end{bmatrix} \\
&= \begin{bmatrix}
I_{m} \cos(\omega t - \delta) \\
I_{m} \sin(\omega t - \delta) \\
0 \\
\end{bmatrix} \end{align*} $$
میتوان دید که مشابه ولتاژ، $$ I_{\alpha} $$ یک تابع کسینوسی، $$ I_{\beta} $$ یک تابع سینوسی و $$ U=I_{0} $$ برابر با صفر است.
محاسبه ماتریس تبدیل
از آنجایی که ولتاژهای سهفاز را میتوان مانند بردارها در صفحه مختلط دوبعدی نمایش داد، برای تبدیل نیز میتوان از ایده مشابهی استفاده کرد. اگر از تجزیه برداری استفاده کنیم، داریم:
$$ \large \begin{align*} U _ { \alpha } =& U _ { a } \cos ( 0 ) - U _ { b } \cos ( \frac { \pi } { 3 } ) - U _ { c } \cos ( \frac { \pi } { 3 } ) \\
U _ { \beta } =& U _ { a } \cos ( \frac { \pi } { 2 } ) + U _ { b } \cos ( \frac { \pi } { 6 } ) - U _ { c } \cos ( \frac { \pi } { 6 } ) \end{align*} $$
برای به دست آوردن توالی صفر، میتوان برای جلوگیری از عدم تعادل بین فازها یا مؤلفه DC، هر ولتاژ فاز را با وزنهای معادل جمع کرد. بنابراین:
$$ \large U _ { 0 } = U _ { a } k _ { 0 } + U _ { b } k _ { 0 } + U _ { c } k _ { 0 } $$
اگر معادله بالا را به فرم ماتریسی بنویسیم، داریم:
$$ \large \begin{bmatrix} U _ { \alpha } \\ U _ { \beta } \\ U _ { 0 } \\ \end{bmatrix} = k _ { 1 } \begin{bmatrix} 1 & - \frac { 1 } { 2 } & -\frac { 1 } { 2 } \\
0 & \frac { \sqrt { 3 } } { 2 } & - \frac { \sqrt { 3 } } { 2 } \\
k _ { 0 } & k _ { 0 } & k _ { 0 } \\
\end{bmatrix} \begin{bmatrix} U _ { a } \\ U _ { b } \\ U _ { c } \\ \end{bmatrix} $$
ضریب $$k_1$$، یک ضریب تصحیح برای حذف اختلافهای تغییر مقیاس است که در اثر ضرب بهوجود آمده است. با توجه به مقادیر استاندارد، این مقادیر $$ k_{1} = \frac{2}{3} $$ و $$ k_{0} = \frac{1}{2} $$ هستند. البته انتخاب مقادیر دیگر برای ضرایب، ممکن است. یک رویکرد دیگر، کاهش بهره ماتریس به یک است.
اکنون بهرهای را محاسبه میکنیم که حاصل از ضرایب ماتریس برای سطر اول است.
$$ \large G = \sqrt { { 1 } ^ { 2 } + { ( - \frac { 1 } { 2 } ) } ^ { 2 } + { ( - \frac { 1 } { 2 } ) } ^ { 2 } } = \sqrt { \frac { 3 }{ 2 } } $$
نتیجه مشابه را میتوان برای سطر دوم به دست آورد. برای کاهش بهره به یک، باید ضرب زیر را به آن افزود:
$$ \large k _ { 1 } = \frac { 1 } { G } = \sqrt { \frac { 2 } { 3 } } $$
و مقدار $$ k_0$$ را میتوان با استفاده از فرمولهای زیر محاسبه کرد:
$$ \begin{align*} \large G _ { 0 } & = \sqrt { 3 { k _ { 0 } } ^ { 2 } } \\
G _ { 0 } & = \sqrt { 3 { k _ { 0 } } ^ { 2 } } \\
\sqrt { 3 { k _ { 0 } } ^ { 2 } } & = \sqrt { \frac { 3 } { 2 } } \\
k _ { 0 } & = \frac { 1 } { \sqrt { 2 } } \end {align*}$$
در نتیجه، فرم ماتریسی زیر را خواهیم داشت:
$$ \large \begin{bmatrix} U _ { \alpha } \\ U _ { \beta } \\ U _ { 0 } \\ \end{bmatrix} = \sqrt { \frac { 2 } { 3 } } \begin {bmatrix} 1 & - \frac { 1 } { 2 } & - \frac { 1 } { 2 } \\
0 & \frac { \sqrt { 3 } } { 2 } & - \frac { \sqrt { 3 } } { 2 } \\
\frac { 1 } { \sqrt { 2 } } & \frac { 1 } { \sqrt { 2 } } & \frac { 1 } { \sqrt { 2 } } \\
\end {bmatrix} \begin {bmatrix} U _ { a } \\ U _ { b } \\ U _ { c } \\ \end {bmatrix} $$
روشهای مختلف، مزایا و معایب متفاوتی دارند. مزیت انتخاب متفاوت ضرایب، ناوردایی یا تغییرناپذیری توان است.
در روش اول، توان را میتوان به صورت زیر نوشت:
$$ \large \begin{align*} S = & {\begin{bmatrix} U _ { a } \\ U _ { b } \\ U _ { c } \\ \end{bmatrix} } ^ T {\begin{bmatrix} I _ { a } \\ I _ { b } \\ I _ { c } \\ \end{bmatrix}} \\ = &
{ ( T _ { \alpha \beta 0 } ^ { - 1 } \begin{bmatrix} U _ { \alpha } \\ U _ { \beta } \\ U _ { 0 } \\ \end{bmatrix} ) } ^ T { ( T _ { \alpha \beta 0 } ^ { - 1 } \begin{bmatrix} I _ { \alpha } \\ I _ { \beta } \\ I _ { 0 } \\ \end{bmatrix} ) } \\
= & { ( \begin{bmatrix} U _ { \alpha } \\ U _ { \beta } \\ U _ { 0 } \\ \end{bmatrix} ) } ^ T { ( T _ { \alpha \beta 0 } ^ { - 1 } ) } ^ T ( T _ { \alpha \beta 0 } ^ { - 1 } ) { ( \begin{bmatrix} I _ { \alpha } \\ I _ { \beta } \\ I _ { 0 } \\ \end{bmatrix} ) } \end{align*} $$
در اینجا، ضرب دو ماتریس تبدیل را میتوان از رویکرد اول محاسبه کرد:
$$ \large { ( T _ { \alpha \beta 0 } ^ { - 1 } ) } ^ T ( T _ { \alpha \beta 0 } ^ { - 1 } ) =
\begin{bmatrix} \frac { 3 } { 2 } & 0 & 0 \\
0 & \frac { 3 } { 2 } & 0 \\
0 & 0 & 3 \\
\end{bmatrix} $$
که منجر به توان زیر میشود:
$$ \large S = U _ { a } I _ { a } + U _ { b } I _ { b } + U _ { c } I _ { c } = \frac { 3 } { 2 } ( U _ { \alpha } I _ { \alpha } + U _ { \beta } I _ { \beta } + 2 U _ { 0 } I _ { 0 } ) $$
البته، در رویکرد دوم ضرایب به یک تقلیل مییابند:
$$ \large { ( T _ { \alpha \beta 0 } ^ { - 1 } ) } ^ T ( T _ { \alpha \beta 0 } ^ { - 1 } ) =
\begin{bmatrix} 1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix} $$
و توان به صورت زیر خواهد بود:
$$ \large S = U _ { a } I _ { a } + U _ { b } I _ { b } + U _ { c } I _ { c } = ( U _ { \alpha } I _ { \alpha } + U _ { \beta } I _ { \beta } + U _ { 0 } I _ { 0 } ) $$
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^











با سلام و تشکر از مطلب تبدیل کلارک در برق. همکاران مقاله ای در زمینه تشخیص نوسان در شبکه برق از فالت به کمک تبدیل کلارک نوشته بوند لذا درباره این تبدیل اطلاعاتی از سایت شما دریافت کردم.