توضیح الگوریتم مرتب سازی شمارشی و پیاده سازی آن در زبان های مختلف

الگوریتم مرتب سازی شمارشی در سال ۱۹۵۴ توسط هارولد سوآرد کشف شد. مرتب‌سازی شمارشی از نوع الگوریتم‌های مرتب‌سازی خطی است. این الگوریتم، پیچیدگی زمانی برابر با $$O(n+k)$$ دارد. n نمایانگر اندازه آرایه ورودی و k نشان‌دهنده اندازه آرایه کمکی Count است. به همین دلیل است که الگوریتم مرتب سازی شمارشی، روشی سریع و قابل اتکا برای مرتب‌سازی داده‌ها است. مرتب‌سازی شمارشی برعکس تکنیک‌های مرتب سازی حبابی و ادغامی، بر اساس مقایسه پایه‌گذاری نشده است. این الگوریتم از مقایسه کردن دوری می‌کند و در مقابل از امتیاز پیچیدگی زمانی $$O(1)$$ برای عملیات‌ وارد کردن و حذف داده‌ها بهره می‌برد. الگوریتم مرتب سازی شمارشی، کلید‌هایی را مرتب می‌کند که از نوع داده عدد صحیح با مقدار کوچک هستند. این کلید‌ها درون محدوده مشخص شده‌ای قرار دارند. الگوریتم مرتب سازی شمارشی با تکنیک شمارش تعداد عناصر با هر مقدار کلید منحصر به فرد کار می‌کند و بعد از آن، از محاسبات خاص ریاضی برای مرتب‌سازی مقدار هر کلید استفاده می‌کند.

در این مطلب از مجله فرادرس با الگوریتم مرتب‌سازی شمارشی آشنا می‌شویم. روش کار این الگوریتم را بررسی کرده و کد‌های مربوط به آن را در زبان‌های برنامه نویسی مختلف پیاده‌سازی می‌کنیم. بعد از آن، وضعیت پیچیدگی‌های زمانی و فضایی مربوط به اجرای مرتب‌سازی شمارشی را توضیح داده‌ایم و همچنین مزایا و معایت استفاده از این الگوریتم را در مقایسه با سایر الگوریتم‌های مرتب‌سازی می‌سنجیم.

الگوریتم مرتب سازی شمارشی چیست؟

الگوریتم مرتب سازی شمارشی را می‌توان در چهار بخش به صورت خلاصه و بسیار شفاف توضیح داد.

• الگوریتم مرتب سازی شمارشی، الگوریتمی است که برای مرتب‌سازی اعداد Integer در علوم کامیپوتری استفاده می‌شود. با کمک این الگوریتم، اشیا را متناظر با کلید‌های برای هر کدام مرتب می‌کنند. این کلیدها از نوع اعداد صحیح مثبت کوچک هستند.
• این الگوریتم با مشخص کردن موقعیت هر جفت کلید-مقدارهای موجود در دنباله خروجی کار می‌کند. این کار با شماردن تعداد اشیای دارای جفت کلیدمقدار و اضافه کردن مجموع پیشوند‌ها بر روی آن شمارش‌ها انجام می‌دهد.
• از آنجا که طول زمان اجرای این الگوریتم متناسب با تعداد آیتم‌های مورد بررسی و اختلاف بین بیشترین و کمترین جفت‌های کلید و مقدار است، فقط برای زمان‌هایی مناسب است که تعداد آیتم‌های مورد مرتب‌سازی خیلی بزرگ‌تر از محدوده کلید‌ها نیستند.
• این الگوریتم به صورت متداولی به عنوان «زیرروال» (Subroutine) تکنیک «مرتب‌سازی مبنایی» (Radix Sort) استفاده می‌شود. مرتب‌سازی مبنایی روشی بسیار کارآمدتر برای مرتب‌سازی کلید‌های بزرگ‌تر است.

بعد از اینکه دانستیم الگوریتم مرتب‌ سازی شمارشی چیست، در بخش بعدی با روند کار این الگوریتم آشنا می‌شویم.

کار با الگوریتم مرتب سازی شمارشی

مرتب‌سازی شمارشی روشی برای مرتب‌سازی داده‌های درون آرایه‌ها در برنامه نویسی است. این الگوریتم وظیفه خود را با کمک بررسی مستقیم هر آیتم و شماردن تعداد رخ‌دادهای آن در آرایه انجام می‌دهد. سپس از تعداد‌های شمارش شده برای هر عنصر در آرایه استفاده می‌کند تا محل قرارگیری آن عنصر را در آرایه مرتب شده تشخیص دهد.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

در ابتدای کار، آرایه فرضی را در نظر می‌گیریم که باید مرتب شود. اولین کار برای حل مسئله این است که بزرگ‌ترین مقدار را در عناصر آرایه پیدا کنیم. سپس این مقدار را به متغیر max تخصیص می‌دهیم.

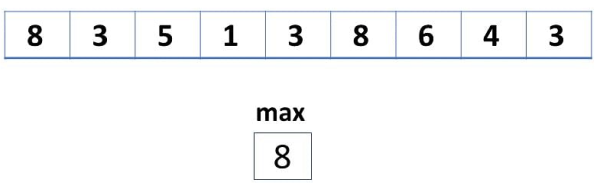
الان برای ذخیره کردن داده‌های مرتب شده، باید آرایه جدیدی را با نام count ایجاد و مقداردهی کنیم. به این صورت که طول آرایه باید برابر با max+1 باشد و همه عناصر با مقدار 0 مقداردهی شوند.

همین‌طور که در تصویر زیر نشان داده شده است، تعداد تکرار هر عنصر در آرایه داده شده را با ایندکس متناظرش در آرایه count ذخیره می‌کنیم.

الان باید «مجموع تجمعی» (Cumulative Sum) یا «مجموع پیشوند» (Prefix Sum) عناصر آرایه count را با انجام محاسبه count[i] = count[i – 1] + count[i] بدست آورد. این عملیات به قرار دادن عناصر آرایه داده شده در ایندکس صحیح مربوط به آن‌ها در آرایه خروجی کمک می‌کند. در نتیجه اجرای این عملیات آرایه count به شکل زیر خواهد شد.

به دلیل اینکه آرایه اصلی دارای ۹ مقدار ورودی است، باید آرایه دیگری با ۹ جایگاه برای ذخیره‌سازی داده‌های ساخته شده به صورت خالی ایجاد کنیم. سپس هر عنصر را از آرایه count انتخاب کرده و در محل صحیح مربوط به خودش در آرایه خروجی قرار می‌دهیم. برای انجام این کار از مقدار مربوط به ایندکس مربوط به آن در آرایه countباید یک واحد کم کنیم. بعد از قرار دادن هر عدد در آرایه خروجی، عدد متناظر آن در آرایه countکه منهای یک واحد شده به همان صورت باقی می‌مانند.

به عنوان نتیجه آرایه ذخیره شده برابر با شکل زیر می‌شود.

روش های ساده برای تسلط به طراحی الگوریتم با فرادرس

الگوریتم مرتب سازی شمارشی یکی از انواع الگوریتم‌های طراحی شده برای مرتب‌سازی اعداد در کامیپوتر است. درک این روش نیاز به تکرار و تمرین دارد و لازمه آن شناخت کافی درباره اصول طراحی و نوشتن الگوریتم است. از طرف دیگر، یکی از روش‌های خوب برای درک طراحی الگوریتم در بهترین حالت ممکن و دانستن روش یادگیری آن، استفاده از کلاس‌ها و دوره‌های آموزشی است. باید توجه کنیم که فیلم‌های آموزشی نسبت به کلاس‌ها از مزیت‌های بیشتری برخوردار هستند. این مزیت‌ها مخصوصا در مطالب کمی پیچیده مانند طراحی الگوریتم باعث تاثیر بسیار بیشتر فیلم‌های آموزشی نسبت به کلاس‌ها می‌شود. در واقع می‌توان گفت معایب موجود در کلاس‌های حضوری بازده این روش آموزش را بسیار کم می‌کند.

در ادامه چند مورد از معایب کلاس‌های حضوری را نسبت به فیلم‌های آموزشی، فهرست کرده‌ایم.

• اولین مشکل اینجاست که موسسات خیلی کمی وجود دارند که طراحی الگوریتم را آموزش دهند.
• در صورت پیدا کردن چنین موسسه‌ای هزینه مالی زیادتری نسبت به فیلم‌های آموزشی باید متقبل شد.
• چنین کلاس‌هایی دارای زمان‌بندی مشخصی هستند که معمولا دانشجو مجبور به تنظیم زمان خود با موسسه است زیرا زمان کلاس با دانشجو تنظیم نمی‌شود.
• کیفیت آموزشی این کلاس‌ها را به‌جز از طریق کسب تجربه نمی‌توان سنجید.

به این منظور و برای راهنمایی بیشتر، فرادرس فیلم‌های آموزشی مختلفی را به صورت اختصاصی در این رابطه تولید و منتشر کرده که در ادامه چند مورد از آن‌ها را معرفی کرده‌ایم.

• فیلم آموزش طراحی الگوریتم فرادرس
• فیلم آموزش طراحی الگوریتم همراه با حل مثال های عملی فرادرس
• فیلم آموزش حل روابط بازگشتی در سایت فرادرس
• فیلم آموزش مروری بر پیچیدگی محاسبات در وب‌سایت فرادرس

پیاده سازی مرتب سازی شمارشی

برای اینکه بتوانیم الگوریتم مرتب سازی شمارشی را به بهترین شکل ممکن پیاده‌سازی کنیم، باید در ابتدا به پیاده‌سازی شبه کد مربوط به این الگوریتم بپردازیم. سپس شکل کلی الگوریتم را استخراج کرده و در نهایت هم از روی این الگوریتم و شبه کد، کدهای مربوط به آن را با زبان برنامه نویسی تخصصی خود بنویسیم.

فیلم آموزش الگوریتم های مرتب سازی در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

شبه کد مرتب سازی شمارشی

شبه کد مربوط به مرتب‌سازی شمارشی را از روی مراحل زیر قدم به قدم پیاده‌سازی می‌کنیم.

1. بر روی آرایه ورودی پیمایش می‌کنیم تا بالاترین مقدار را پیدا و در متغیر maxذخیره کنیم.
2. آرایه جدیدی را با مقادیر 0 و اندازه max+1 تعریف می‌کنیم.
3. هر عنصر درون آرایه را بشماریم و مقدار مربوط به ایندکس متناظر آن را در آرایه کمکی افزایش بدهیم.
4. برای پیدا کردن مقدار مجموع تجمعی، مقدارهای فعلی و قبلی هر عنصر را در آرایه کمکی با یکدیگر جمع می‌بندیم.
5. الان مقدار تجمعی، جایگاه واقعی عنصرها را در آرایه ورودی مرتب شده نشان می‌دهند.
6. پیمایش را بر روی آرایه کمکی از جایگاه با شماره ۰ شروع کرده و تا بالاترین مقدار ادامه می‌دهیم.
7. در ایندکس متناظر با هر کدام مقدار 0 قرار می‌دهیم و مقدار countرا یک واحد کم می‌کنیم. این کار جایگاه دوم عنصر را در آرایه ورودی نشان می‌دهد. البته به شرطی که وجود داشته باشد.
8. الان آرایه‌ای را که در مرحله قبل بدست‌ آورده‌ایم، در آرایه واقعی خروجی مرتب شده قرار می‌دهیم.

پیاده سازی کدهای مربوط به مرتب سازی شمارشی

در این قسمت از مطلب، کدهای مربوط به این الگوریتم را در ۵ زبان برنامه‌نویسی مختلف ارائه داده‌‌ایم.

زبان برنامه نویسی جاوا

کادر زیر کدهای مربوط به الگوریتم مرتب‌سازی شمارشی را با زبان برنامه نویسی جاوا نمایش می‌دهد.

زبان برنامه نویسی #C

کادر زیر کدهای مربوط به الگوریتم مرتب‌سازی شمارشی را با زبان برنامه نویسی #C نمایش می‌دهد.

زبان برنامه نویسی جاوا اسکریپت

زبان جاوا اسکریپت یکی از زبان‌های برنامه‌نویسی محبوب برنامه‌نویسان در دنیا است. برای آشنا شدن با این زبان در سریع‌ترین زمان ممکن و کدنویسی به صورت خوب، می‌توانید مطلب مربوط به ۱۴ مفهوم بنیادی جاوا اسکریپت به زبان ساده از مجله فرادرس را مطالعه کنید.

در کادر زیر کدهای مربوط به الگوریتم مرتب‌سازی شمارشی را با زبان برنامه نویسی جاوا اسکریپت پیاده‌سازی کرده‌ایم.

زبان برنامه نویسی ++C

در کادر زیر کدهای مربوط به الگوریتم مرتب‌سازی شمارشی را با زبان برنامه نویسی ++C پیاده‌سازی کرده‌ایم.

زبان برنامه نویسی پایتون

کادر زیر کدهای مربوط به الگوریتم مرتب‌سازی شمارشی را با زبان برنامه نویسی پایتون نمایش می‌دهد.

پیچیدگی های مرتب سازی شمارشی

برای ارزشیابی هر الگوریتم، باید پیچیدگی زمانی و فضایی آن الگوریتم را محاسبه کرد. این اطلاعات کمک زیادی در انتخاب الگوریتم بهینه برای حل مسائل می‌کنند. در این قسمت نیز به سراغ بررسی پیچیدگی‌های الگوریتم مرتب سازی شمارشی رفته‌ایم.

ادامه مطلب را با بررسی «پیچیدگی زمانی» (Time Complexity) این الگوریتم ادامه می‌دهیم.

پیچیدگی زمانی مرتب سازی شمارشی

مرتب‌سازی شمارشی، زمانی را برای پیدا کردن اندازه بزرگترین عنصر در آرایه صرف می‌کند. این زمان را معادل با k در نظر می‌گیریم. مقداردهی اولیه آرایه countهم به اندازه kثانیه زمان صرف می‌کند. به حافظه سپردن آرایه countنیز به میزان kواحد زمانی مصرف می‌کند. مرتب‌سازی واقعی هم با پیمایش بر روی آرایه ورودی به صورت خطی انجام می‌شود. از این رو که همه مراحل قبل، فارق از آرایه ورودی ثابت بودند، میزان پیچیدگی زمانی در هر سه حالت بهترین، بدترین و میانگین سناریو‌های موجود، مقدار ثابتی خواهد شد.

بهترین حالت

وقتی که همه عناصر آرایه ورودی در محدوده یکسانی باشند، یا وقتی که k برابر با 1 شود، بهترین حالت ممکن برای پیچیدگی زمانی در این الگوریتم رخ می‌دهد. در این سناریو، شماردن رخدادهای هر عنصر در محدوده ورودی به اندازه زمان ثابتی صرف می‌کند. به همین‌ ترتیب، پیدا کردن مقدار ایندکس صحیح هر عنصر در آرایه مرتب شده خروجی به اندازه n واحد زمانی صرف می‌کند. در نتیجه پیچیدگی زمانی کل برابر با$$O(1 + n)$$می‌شود که در واقع برابر با $$O(n)$$ است. یعنی پیچیدگی زمانی این الگوریتم به صورت خطی افزایش پیدا می‌کند.

بدترین حالت

بدترین سناریو ممکن برای پیچیدگی زمانی، وجود داده‌های کج است. به این معنی که بزرگترین عنصر با فاصله خیلی زیادی بسیار بزرگتر از سایر عناصر آرایه است. این مسئله محدوده k را گسترش می‌دهد.

خوب تا به اینجا دانستیم که پیچیدگی زمانی این الگوریتم برابر با O(n+k) است. وقتی که k از مرتبه$$O(n^2)$$باشد، پیچیدگی زمانی برابر با$$O(n+(n^2))$$می‌شود، که ضرورتا به اندازه$$O(n^2 )$$کاهش می‌یابد. وقتی که k از مرتبه$$O(n^3)$$باشد، پیچیدگی زمانی برابر با$$O(n+(n^3))$$می‌شود، که ضرورتا به اندازه$$O(n^3 )$$کاهش می‌یابد. در نتیجه پیچیدگی زمانی در این سناریو افزایش پیدا کرده‌ است. پس برای مقادیر بزرگ k برابر با$$O(k)$$می‌شود. اما مسئله همینجا به پایان نمی‌رسد، بلکه برای مقادیر بسیار بزرگ‌تر k همه چیز به‌طرز قابل توجهی بدتر نیز می‌شود.

پس بدترین پیچیدگی زمانی، وقتی روی می‌دهد که محدوده k در مرتب‌سازی شمارشی، بزرگ باشد.

حالت میانگین

برای محاسبه کردن میزان میانگین پیچیدگی زمانی، مقدار N را ثابت می‌کنیم و مقادیر مختلفی از k را از ۱ گرفته تا بی‌نهایت در نظر می‌گیریم. در این سناریو k به اندازه$$(k+1/2)$$محاسبه می‌شود. و حالت میانگین نیز به اندازه$$N+(K+1)/2$$به دست می‌آید. اگرچه به‌خواطر رویکرد k به سمت بی‌نهایت، پارامتر k به عامل غالب در این فرمول تبدیل می‌شود. در نهایت میزان میانگین پیچیدگی زمانی$$O(N+K)$$را بدست می‌آوریم.

پیچیدگی فضایی مرتب سازی شمارشی

در این رویکرد برای مرتب‌سازی از آرایه کمکی به نام فرضی C با اندازه k در فرایند بالا استفاده کرده‌ایم. در اینجا kبرابر با بیشترین عنصر موجود در آرایه داده شده است. در نتیجه الگوریتم مرتب‌ سازی شمارشی «پیچیدگی فضایی» (Space Complexity) برابر با$$O(k)$$دارد.

محدوده بزرگتر عناصر درون آرایه خاص باعث بزرگتر شدن پیچیدگی فضایی می‌شود. بنابراین پیچیدگی فضایی الگوریتم مرتب سازی شمارشی در صورت بزرگ شدن بیش از حد محدوده اعداد صحیح به‌طرز وحشتناکی رشد می‌کند. زیرا آرایه کمکی به همان اندازه باید ایجاد شود.

دروس آکادمیک در رابطه با طراحی الگوریتم با فرادرس

این قسمت از مطلب به طور خاص مناسب دانشجویانی طراحی شده است که نه تنها تمایل به دانستن چیستی طراحی الگوریتم دارند بلکه باید برای آزمون‌های دانشگاهی و کنکور ارشد نیز آماده شوند. وب‌سایت آموزشی فرادرس فیلم‌های بسیار خوبی درباره الگوریتم با استفاده از اساتید حرفه‌ای و تجزیه و تحلیل سوالات کنکور سال‌های متمادی تهیه کرده است.

در این بخش چند مورد از این فیلم‌های آموزشی را معرفی می‌کنیم. این فیلم‌ها هم برای دانشجویان و هم برای برنامه‌نویسان و افرادی که می‌خواهند با مبحث طراحی الگوریتم تا حد بسیار خوبی آشنا شوند مفید است.

• فیلم آموزش طراحی الگوریتم همراه با مرور و تست کنکور ارشد فرادرس
• فیلم آموزش پیشرفته ساختمان داده به همراه حل سوالات کنکور ارشد و دکتری فرادرس
• فیلم آموزش روش تقسیم و حل در طراحی الگوریتم همراه با مرور و تست کنکور کارشناسی ارشد فرادرس
• فیلم آموزش رابطه های بازگشتی در طراحی الگوریتم و ساختمان گسسته به‌همراه مرور و تست کنکور ارشد فرادرس

در قسمت بعدی به مقایسه الگوریتم‌های شمارشی با روش‌های مرتب‌سازی گوناگون پرداخته‌ایم.

مقایسه مرتب سازی شمارشی با سایر انواع الگوریتم ها

در این بخش الگوریتم‌ مرتب‌سازی شمارشی را در مقایسه با سایر الگوریتم‌ها بررسی کرده‌ایم.

فیلم آموزش مرتب سازی در الگوریتم و پردازش موازی (رایگان) در فرادرس

کلیک کنید

• اگر طول لیست ورودی به اندازه قابل توجهی کوچکتر از بزرگترین مقدار کلید - k در آرایه ورودی - نباشد، زمان اجرایی مرتب‌سازی شمارشی، برابر با$$O(n)$$می‌شود. در عوض، هر الگوریتم مرتب‌سازی مقایسه محوری، نیاز به تعداد$$O(n log n)$$عدد مقایسه دارد.
• در موقعیت‌هایی که گستره عناصر ورودی، قابل مقایسه با تعداد عناصر ورودی است، مرتب‌سازی شمارشی به طور خاصی کارآمد است. مخصوصا از آن جهت که این الگوریتم، مرتب‌سازی را در زمان خطی به انتها می‌رساند. این نکته نسبت به سایر الگوریتم‌های مرتب‌سازی مانند «مرتب سازی سریع» (Quick Sort) می‌تواند به عنوان مزیت در نظر گرفته شود. مرتب‌سازی سریع در بدترین حالت خود دارای پیچیدگی زمانی برابر با$$O(n^2)$$است، در حالی که مرتب‌سازی شمارشی فقط به پیچیدگی زمانی برابر با$$O(n)$$نیاز دارد البته به شرطی که گستره عناصر خیلی وسیع نباشد.
• اکثریت الگوریتم‌های مرتب‌سازی، در زمان مربعی$$O(n^2)$$اجرا می‌شوند. به غیر از «مرتب‌سازی هرمی» (Heap Sort) و «مرتب‌ سازی ادغامی» (Merge Sort)، پیچیدگی زمانی اجرای این الگوریتم‌های مرتب‌سازی برابر با$$O(n log n)$$است. مرتب‌سازی شمارشی تنهای روش مرتب‌سازی است که در زمان خطی اجرا می‌شود.
• از آنجا که هیچ کدام از عنصرها در این تکنیک مقایسه نمی‌شوند، الگوریتم مرتب‌ سازی شمارشی از همه تکنیک‌های بر پایه مقایسه، بهتر عمل می‌کند.
• مزیت‌های خاص، الگوریتم مرتب سازی شمارشی مانند عملکرد عالی بر روی اعداد محدود، کوچک و به خوبی تعریف شده، این الگوریتم را به گزینه بسیار مناسبی به عنوان زیربرنامه‌ای برای سایر الگوریتم‌های مرتب‌سازی مانند «مرتب‌سازی مبنایی» (Radix Sort) تبدیل کرده است. در نتیجه برای اجرای عملیات بزرگ بر روی گستره پهناوری از اعداد هم مناسب شده است.

در بخش بعدی چند مورد از کاربردهای الگوریتم مرتب سازی شمارشی را بررسی کرده‌ایم.

کاربردهای تکنیک مرتب‌ سازی شمارشی

کاربردهای این الگوریتم سریع را می‌توان به صورت خلاصه در ۵ بند زیر بیان کرد.

1. در مواردی که گستره داده‌های ورودی خیلی بزرگ‌تر از تعداد اشیایی که باید مرتب شوند نباشد. در چنین مواردی مرتب‌سازی شمارشی به صورتی کارآمد کار می‌کند. به عنوان مثال، سناریویی را در نظر بگیرید که داده‌ها برابر با 10, 5, 10K و 5K باشند و توالی ورودی از 1 باشد تا 10K.
2. روش مرتب‌سازی این الگوریتم بر اساس مقایسه پایه‌گذاری نشده است.  در نتیجه، پیچیدگی زمانی این الگوریتم در زمان اجرا برابر با$$O(n)$$است و نیازمندی فضایی نیز متناسب با محدوده داده‌ها دارد.
3. از این الگوریتم به صورت متداولی به عنوان زیرروال در سایر الگوریتم‌های مرتب‌سازی مانند مرتب‌سازی مبنایی استفاده می‌شود.
4. مرتب‌سازی شمارشی، وجود هر شی داده‌ای درون O را با استفاده از هش‌کردن جزئی به مقدار 1 محاسبه می‌کند.
5. از مرتب‌سازی شمارشی می‌توان بر روی داده‌های ورودی منفی نیز استفاده کرد.

جمع بندی

الگوریتم مرتب سازی شمارشی، یکی از الگوریتم‌های مخصوص مرتب سازی اعداد صحیح است. این الگوریتم بر اساس مقایسه کار نمی‌کند، بنابراین پیچیدگی زمانی کمتری نسبت به سایر الگوریتم‌های مرتب‌سازی مقایسه محور دارد. کلا برای کار با داده‌ها بهتر است که با انواع الگوریتم‌های مرتب‌سازی آشنا شویم. کار طراحی و پیاده‌سازی الگوریتم‌ها در حل مسائل برنامه‌نویسی یکی از توانایی‌های برنامه‌نویسان حرفه‌ای است.

در این مطلب از مجله فرادرس درباره الگوریتم مرتب‌سازی شمارشی صحبت کرده‌ایم. در ابتدای کار با این الگوریتم آشنا شده و سپس روش کار این الگوریتم را بررسی کردیم. در ادامه درباره پیچیدگی‌های فضایی و زمانی این الگوریتم بحث کرده و در نهایت هم کارآیی مرتب‌سازی شمارشی را با کارآمدی سایر انواع الگوریتم‌ها مقایسه کردیم.