آینه جریان ویلسون (Wilson) — از صفر تا صد

آینه جریان ویلسون به افتخار جورج ویلسون (George Wilson) مخترع آن، نام‌گذاری شده است. این مدار یک راه حل مبتکرانه و عالی برای خطای بتای محدود (Finite-β) در آینه جریان BJT ساده است. در این آموزش قصد داریم تا به توضیح آینه جریان ویلسون بپردازیم و معادلات جریان و مقاومت خروجی آن را به دست آوریم.

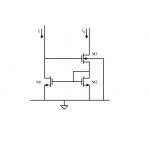
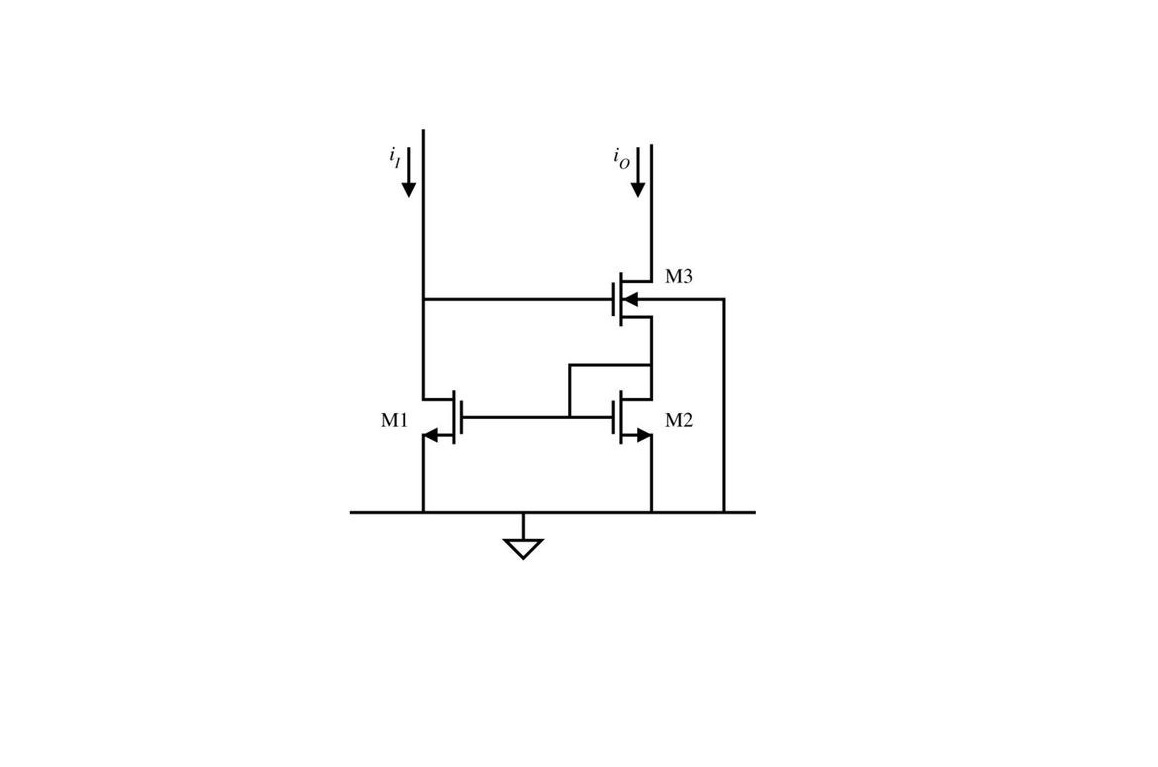
شکل زیر مدار آینه جریان BJT ساده را نشان می‌دهد.

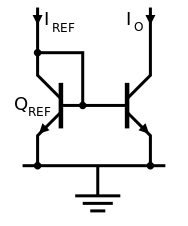
معادلات جریان در آینه جریان ویلسون

به منظور عملکرد صحیح در یک مدار آینه جریان، شرایط زیر باید برقرار باشد:

1. ترانزیستورهای Q1 و Q2 کاملا مشابه باشند. پس جریان کلکتور (Collector) آن‌ها برای یک جریان بیس (Base) یکسان برابر است.
2. هر سه ترانزیستور دارای بهره جریان امیتر مشترک (Common-Emitter) یکسانی (β) باشند.

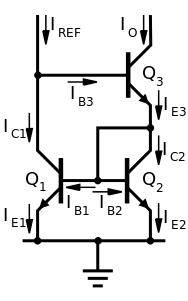
از آنجا که Q1 و Q2 دارای ولتاژهای امیتر (متصل به زمین) و بیس (متصل به یکدیگر) یکسانی هستند، پس جریان بیس آنها یکسان خواهد بود. به این جریان $$I_B$$ می‌گوییم:

$${\displaystyle I_{B1}=I_{B2}=I_{B}\,} \;\;\;\;\; (1)$$

از معادله بالا می‌توان گفت که جریان کلکتور در Q1 و Q2 یک مقدار یکسان خواهند بود:

$${\displaystyle I_{C1}=I_{C2}=I_{C}\,}\; \;\; \;\; (2)$$

حال از معادلات پایه مربوط به ترانزیستور BJT جریان بیس مربوط به ترانزیستور Q3 به صورت زیر محاسبه می‌شود:

$${\displaystyle I_{B3}={\frac {I_{O}}{\beta }}} \;\;\;\;\; (3)$$

همچنین برای مقدار جریان امیتر داریم:

$${\displaystyle I_{E3}={\frac {\beta +1}{\beta }}I_{O}} \;\;\;\;\; (4)$$

با استفاده از KCL در مدار آینه جریان ویلسون، معادله زیر را به دست می‌آوریم:

$${\displaystyle I_{E3}=I_{C2}+I_{B1}+I_{B2}\,} \;\;\;\;\; (5)$$

با جایگذاری معادلات اول و دوم در معادله بالا داریم:

$${\displaystyle I_{E3}=I_{C}+2I_{B}\,} \;\;\;\;\; (6)$$

با توجه به $$I_{C}=βI_{B}$$ که از شرط دوم و معادلات پایه ترانزیستور BJT به دست آمده است:

$${\displaystyle I_{E3}=I_{C}+2{\frac {I_{C}}{\beta }}=I_{C}\left(1+{\frac {2}{\beta }}\right)=I_{C}\left({\frac {2+\beta }{\beta }}\right)}\;\;\;\;\; (7)$$

با جایگذاری معادله چهارم در معادله بالا داریم:

$${\displaystyle I_{O}\left({\frac {\beta +1}{\beta }}\right)=I_{C}\left({\frac {2+\beta }{\beta }}\right)} \;\;\;\;\;(8)$$

 برای به دست آوردن $$I_{C}$$ معادله بالا را بازنویسی می‌کنیم:

$${\displaystyle I_{C}=I_{O}\left({\frac {\beta +1}{\beta +2}}\right)} \;\;\;\;\;(9)$$

حال با در نظر گرفتن جریان مرجع ($$I_{REF}$$) و با استفاده از KCL و جایگذاری در معادله دوم، به رابطه زیر می‌رسیم:

$${\displaystyle I_{REF}=I_{C1}+I_{B3}=I_{C}+I_{B3}\,} \;\;\;\;\;(10)$$

با استفاده از معادلات شماره (3) و (9) و (10) داریم:

$${\displaystyle I_{REF}=I_{O}\left({\frac {\beta +1}{\beta +2}}\right)+{\frac {I_{O}}{\beta }}=I_{O}\left({\frac {\beta +1}{\beta +2}}+{\frac {1}{\beta }}\right)\,} $$

معادله را بار دیگر بازنویسی می‌کنیم:

$${\displaystyle I_{O}={\frac {I_{REF}}{\left({\frac {\beta +1}{\beta +2}}+{\frac {1}{\beta }}\right)}}}$$

سرانجام با ساده‌سازی و فاکتورگیری جریان خروجی را به دست می‌آوریم:

$${\displaystyle I_{O}={\frac {I_{REF}}{1+{\frac {2}{\beta \left(\beta +2\right)}}}}} $$

واضح است که حتی اگر β نسبتا کوچک باشد، مقدار $$β(β+2)$$ خیلی بزرگ خواهد بود، در نتیجه مخرج در معادله بالا به یک میل می‌کند. بنابراین مقدار $$I_{O}$$ به مقدار $$I_{REF}$$ میل خواهد کرد.

$${\displaystyle \lim \limits _{\beta \to \infty }\left({I_{O}}\right)=I_{REF}} $$

برای مثال برای یک ترانزیستور با مقادیر متوسط β=50، از نظر تئوری می‌توان انتظار انحراف جریان در حد 0.75μA را داشت. برای مقدار β=150 این مقدار به 87nA کاهش می‌یابد.

باید به این نکته بسیار مهم توجه کرد که آینه جریان ویلسون یک منبع جریان ثابت نیست. اگر ولتاژ تغذیه V_CC تغییر کند، مقدار جریان خروجی نیز تغییر خواهد کرد. فرض کنید جریان مرجع  $$I_{REF}$$ توسط یک مقاومت متصل به منبع جریان به دست آید. همچنین فرض کنید $$V_{BE}$$ برای تمام ترانزیستورها دارای مقدار 0.7V باشد. در نتیجه ولتاژ بیس ترانزیستورهای Q1 و Q2 مقدار 0.7V خواهد بود، زیرا امیتر این ترانزیستورها به زمین متصل است. مقدار ولتاژ بیس ترانزیستور Q3 نیز برابر با $$0.7+0.7=1.4 V$$ خواهد شد. حال مقدار جریان مرجع به صورت زیر است:

$${\displaystyle I_{REF}={\frac {V_{CC}-1.4}{R_{REF}}}} $$

بنابراین مقدار جریان خروجی نیز به ولتاژ تغذیه وابسته خواهد بود. یک منبع جریان ثابت به عنوان جریان مرجع می‌تواند یک جریان خروجی ثابت را تضمین کند.

مقاومت خروجی آینه جریان ویلسون

مدل سیگنال کوچک آینه جریان ویلسون را در نظر بگیرید که در تصویر زیر نشان داده شده است. ترانزیستورها با مدل سیگنال کوچک T جایگزین شده و در شکل توسط یک ترانزیستور سیگنال بزرگ BJT موازی با مقاومت خروجی سیگنال کوچک $$r_O$$ نشان داده شده‌اند. مقاومت‌های خروجی ترانزیستورهای Q1 و Q2 نیز در این مدل حضور دارند، اما چون در این تحلیل نقشی ندارند، از آن‌ها صرف نظر شده است. جریان مرجع در مدل سیگنال کوچک غیرفعال در نظر گرفته می‌شود، به این معنی که بیس ترانزیستور Q3 به کلکتور Q1 متصل شده است.

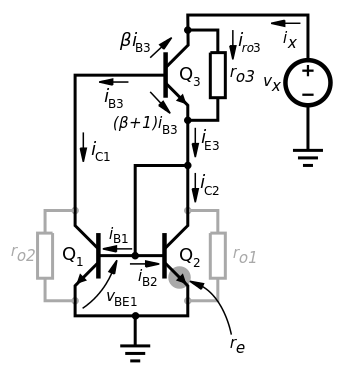
مقدار مقاومت خروجی آینه جریان ویلسون ($$R_O$$) را از طریق اعمال ولتاژ $$V_x$$ به خروجی و یافتن رابطه بین این ولتاژ با جریان خروجی یعنی $$I_x$$ می‌یابیم. ابتدا توجه کنید که جریان از بیس ترانزیستور Q3 خارج می‌شود و جریان‌های کلکتور و امیتر در Q3 به کلکتور ترانزیستور Q1 متصل هستند. البته این مقدارها مربوط به مدل سیگنال بزرگ ترانزیستور BJT هستند و با مقادیر $$I_{C3}$$ و $$I_{E3}$$ تفاوت دارند، اما مقدار $$I_{B3}$$ در هر دو یکسان است. این کار فقط برای حذف منفی از مقادیری است که در آنالیز به دست خواهد آمد و اگر معکوس نشوند نتایج به دست آمده تغییری نخواهد کرد.

همان طور که قبلا اشاره شد، ترانزیستورهای Q1 و Q2 به یکدیگر متصل هستند؛ بنابراین جریان کلکتورها و نیز جریان بیس‌ها یکسان هستند. از این به بعد برای سادگی جریان کلکتور را $$i$$ می‌نامیم. جریان کلکتور ترانزیستور Q1 با جریان بیس ترانزیستور Q3 برابر است. در نتیجه داریم:

$${\displaystyle i_{C1}=i_{C2}=i_{B3}=i\,}$$

از معادلات امیتر مشترک مقدار جریان بیس به صورت زیر است:

$${\displaystyle i_{B1}=i_{B2}={\frac {i}{\beta }}}$$

از معادلات امیتر مشترک می‌توان جریان کلکتور و امیتر سیگنال بزرگ BJT در Q3 را نیز به دست آورد. از طریق اعمال KCL نشان داده می‌شود که در اتصال کلکتور-بیس Q2 داریم:

$${\displaystyle i_{E3}=i_{B1}+i_{B2}+i_{C2}={\frac {2i}{\beta }}+i}$$

$${\displaystyle i_{E3}=i\left(1+{\frac {2}{\beta }}\right)} $$

ولتاژ بیس-امیتر Q1 و Q2 یعنی ($$V_{BE1}$$) برابر با حاصل ضرب جریان امیتر در مقاومت بیس-امیتر سیگنال بزرگ (در مدل T با $$r_e$$ نشان داده می‌شود) است:

$${\displaystyle v_{be1}=\left(\beta +1\right){\frac {i}{\beta }}r_{e}=i\left({\frac {\beta +1}{\beta }}\right)r_{e}} $$

از طریق KCL در محل اتصال کلکتور Q3 و مقاومت خروجی، مقدار جریان در مقاومت خروجی Q3 ($$i_{ro3}$$) به صورت زیر است:

$${\displaystyle i_{ro3}=i\left(1+{\frac {2}{\beta }}\right)+i\left(\beta +1\right)}$$

$${\displaystyle i_{ro3}=i\left(\beta +2+{\frac {2}{\beta }}\right)}$$

با اعمال قانون اهم، می‌توانیم ولتاژ در مقاومت خروجی را به دست آوریم:

$${\displaystyle v_{ro3}=i\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}} $$

بنابراین، ولتاژ $$V_x$$ برابر با مجموع این ولتاژ و ولتاژ بیس-امیتر در Q1 و Q2 است:

$${\displaystyle v_{x}=i\left({\frac {\beta +1}{\beta }}\right)r_{e}+i\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}} $$

جریان $$i_x$$ را می‌توان با اعمال KCL در گره بالای مقاومت خروجی Q3 به دست آورد:

$${\displaystyle i_{x}=i_{ro3}-\beta i=i\left(2+{\frac {2}{\beta }}\right)} $$

مقاومت خروجی $$R_O$$ به صورت زیر به دست می‌آید:

$${\displaystyle R_{o}={\frac {v_{x}}{i_{x}}}}$$

با صرف نظر از فاکتورهای $$i$$، معادله واحدی به صورت زیر به دست می‌آید:

$${\displaystyle R_{o}={\frac {\left({\frac {\beta +1}{\beta }}\right)r_{e}+\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}}{2+{\frac {2}{\beta }}}}}$$

مقدار $$r_e$$ برابر با $$ {\displaystyle r_{e}={\frac {\beta }{\beta +1}}{\frac {1}{g_{m}}}} $$ است. دقت کنید که کسر اولی به دلیل اینکه بتا اغلب بزرگ است برابر یک می‌شود، پس فقط $${\displaystyle {\frac {1}{g_{m}}}}$$ باقی می‌ماند. از آنجا که $${\displaystyle {\frac {1}{g_{m}}}}$$ اغلب از مرتبه 20mS است، این عبارت تقریبا 50Ω خواهد بود. در نظر داشته باشید که این مقدار قرار است با عبارت شامل β (در بازه 100) جمع شده و سپس ضرب در $$r_o$$ (در بازه 50kΩ) شود، بنابراین مقدار بسیار ناچیزی است. پس با تقریب بسیار خوبی می‌توان نوشت:

$${\displaystyle R_{o}\approx {\frac {\left(\beta +2+{\frac {2}{\beta }}\right)r_{o}}{2+{\frac {2}{\beta }}}}}$$

حال صورت و مخرج را در β ضرب می‌کنیم:

$${\displaystyle R_{o}\approx {\frac {\left(\beta ^{2}+2\beta +2\right)r_{o}}{2\beta +2}}} $$

اکنون می‌توان گفت زمانی که β مقدار بزرگی داشته باشد، عدد ثابت 2 در مقایسه ۲β در مخرج خیلی کوچکتر و قابل صرف نظر است. همچنین می‌توان گفت عبارت 2β در صورت کسر نیز در مقایسه با β² ناچیز است. نتیجه به دست آمده با در نظر گرفتن این تقریب‌ها حتی برای کاربردهای عملی هم دارای دقت کافی است. با حذف این عبارات و تقسیم صورت و مخرج بر β معادله به دست آمده به صورت زیر است:

$${\displaystyle R_{o}\approx {\frac {\beta r_{o}}{2}}} $$

برای مقدار β=100 و r_o=50KΩ و r_e=50Ω مقدار محاسبه شده با استفاده از معادله کامل برابر با 2٫53MΩ و با معادله دارای تقریب برابر با 2٫5KΩ است. همان طور که دیده می‌شود، تقریب دارای دقت کافی است و ارزش بالایی از حیث ساده‌سازی معادله دارد، مخصوصا در کاربردهای عملی که معمولا تغییرات بیشتر از مقدار این خطا است. این مثال همچنین امپدانس بزرگ آینه جریان ویلسون حتی برای مقادیر متوسط β را نشان می‌دهد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی الکترونیک
• آموزش الکترونیک ۲
• مجموعه آموزش‌های مهندسی برق
• آموزش مبانی مهندسی برق 1
• تقویت کننده امیتر مشترک (Common Emitter Amplifier) — مفاهیم پایه
• تقویت کننده JFET سورس مشترک (Common Source JFET Amplifier) — به زبان ساده

^^