پله پتانسیل (Potential Step) — به زبان ساده

در این مقاله در نظر داریم تا با زبانی ساده به بررسی یکی از مهم‌ترین مسائل فیزیک کوانتوم مقدماتی، یعنی پله پتانسیل (Potential Step) توسط معادله مشهور شرودینگر بپردازیم.

در مقاله «معادله شرودینگر -- به زبان ساده» با نحوه به دست آوردن معادله موجی آشنا شدیم که امواج وابسته به مواد یا به اصطلاح امواج ماده (Matter wave) را توصیف می‌کرد. معادله موج مذکور که توسط اروین شرودینگر (Erwin Schrödinger) ارائه شد، یک معادله دیفرانسیل مرتبه دوم بوده که به سادگی تنها با دو شرط مرزی می‌توان آن را حل کرد.

پله پتانسیل

یکی از مهم‌ترین مسائل مقدماتی که در فیزیک کوانتومی مورد بررسی قرار می‌گیرد، مسئله پله پتانسیل است.

فیلم آموزش مکانیک کوانتومی 1 – جامع و با نکات کاربردی در فرادرس

کلیک کنید

مسئله مذکور به بررسی ذره‌ای می‌پردازد که در تمامی فضا آزاد ولی در نقطه‌ای خاص یکباره با پتانسیل $$V_{0}$$ روبه‌رو می‌شود.

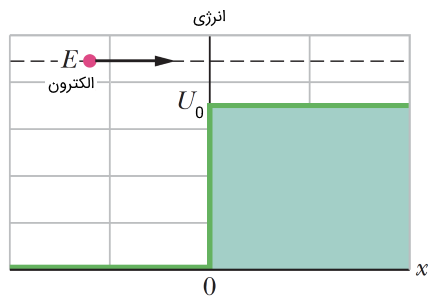
معمولاً جهت سادگی محاسبات، پتانسیل را در نقطه $$x = 0$$ بررسی می‌کنند. پتانسیل مذکور برای ذره می‌تواند از نوع جاذبه یا دافعه باشد. از لحاظ ریاضی پتانسیل موجود در مسئله پله پتانسیل را می‌توانیم به صورت زیر نمایش دهیم:

$$\large V(x) = \begin{cases}0 & x < 0\\V_{0} & x \geq 0\end{cases}$$
(1)

هدف از حل مسئله پله پتانسیل، بررسی دینامیکی شاری از ذرات یکسان با جرم $$m$$ است که با سرعت یکسان $$v$$ از سمت چپ به راست (به سمت پله پتانسیل) حرکت می‌کنند. با توجه به دو شکل (3) و (5)، دو حالت ممکن برای ذرات مذکور وجود دارد. حالت اول این است که انرژی ذرات بیشتر از انرژی پتانسیل و حالت دوم این است که انرژی ذرات کمتر از انرژی پتانسیل پله باشد.

در وهله اول حالتی را بررسی می‌کنیم که انرژی ذرات بیشتر از انرژی پله پتانسیل باشد (شکل 3).

حالت $$\large E\ >\ V_{0}$$

همان‌طور که اشاره کردیم نقطه‌ شروع پتانسیل $$V_{0}$$ را $$x = 0$$ در نظر می‌گیریم. با توجه به شکل (3)، ذرات در مکان‌های $$x < 0$$ آزاد (پتانسیل صفر) بوده و در مکان‌های $$x \geq 0$$ همواره تحت تاثیر پتانسیل ثابت $$V_{0}$$ است.

جهت اینکه درک بهتری از مسئله چاه پتانسیل داشته باشیم، ابتدا از دیدگاه فیزیک کلاسیکی به بررسی مسئله می‌پردازیم. این امر در مقایسه‌ بین دو دیدگاه کلاسیکی و کوانتومی فیزیک حائز اهمیت است.

دیدگاه کلاسیکی

از نقطه نظر فیزیک کلاسیک، ذرات با تکانه ثابت $$p = \sqrt{ 2 m E }$$ از سمت چپ حرکت و به سمت پله پتانسیل می‌آیند. هنگامی که ذرات به ناحیه $$x \geq 0$$ وارد شوند، همواره تحت تاثیر پتانسیل ثابت $$V_{0}$$ قرار می‌گیرند. در نتیجه تکانه آن‌ها کاهش یافته و برابر با مقدار زیر می‌شود:

$$\large p = \sqrt{ 2 m ( E - V_{0} ) }$$
(2)

از آنجایی که انرژی ذرات بزرگ‌تر از انرژی پتانسیل پله ($$E\ >\ V_{0}$$) است، ذرات انرژی لازم جهت عبور کامل از پله پتانسیل را خواهند داشت. در نتیجه مقدار عددی زیر رادیکال در رابطه فوق مثبت می‌شود. با این اوصاف، ذرات تکانه فوق را در تمام ناحیه $$x \geq 0$$ دارند که به معنی انرژی جنبشی کمتر ($$K = E - V_{0}$$) است. از نقطه نظر مکانیک کلاسیک، مسئله پله پتانسیل با شرط $$E\ >\ V_{0}$$ یک مسئله ساده پراکندگی (scattering) در یک بعد است.

شاید شکل (۲) جهت درک بهتر مفهوم پله پتانسیل مناسب باشد. شکل زیر سیمی را نشان می‌دهد که در مکان‌هایی $$x < 0$$، به پتانسیل صفر و در مکان‌های $$x > 0$$، به پتانسیل (ولتاژ) $$V_{0} < 0$$ متصل است. الکترون در غالب جریان الکتریکی با انرژی مشخصی به سمت راست حرکت کرده و با پتانسیل $$V_{0} < 0$$ روبه‌رو می‌شود. از آنجایی که بار الکترون منفی و ولتاژ نیز منفی است، انرژی پتانسیل طبق رابطه $$U = qV$$ مثبت می‌شود. نمودار انرژی پتانسیل مطابق با شکل (۲) را بسته به مقدار انرژی $$E$$ الکترون، می‌توان در شکل (3) یا (5) مدل کرد.

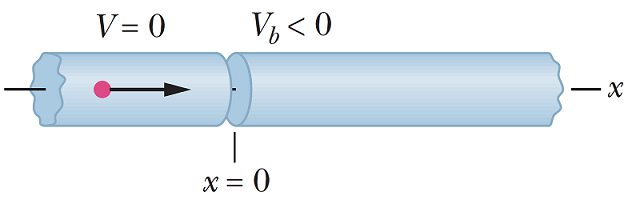
توجه داشته باشید که در سراسر این مقاله، انرژی پتانسیل را برای مسئله پله پتانسیل، بجای نماد $$U$$ با نماد $$V_{0}$$ نشان می‌دهیم.

دیدگاه کوانتومی

همان‌طور که می‌دانید، دینامیک ذرات در مکانیک کوانتومی به صورت موجی توسط معادله شرودینگر بررسی می‌شود. لویی دوبروی به هر ذره مادی که با تکانه $$p$$ حرکت می‌کند، موجی با طول موج $$\lambda = \frac{h}{p}$$ نسبت داد. معادله شرودینگر در یک بعد به فرم زیر است:

$$\large - \frac{ \hbar^{2} }{2m} \frac{\text{d}^{2} \psi ( x) }{\text{d}x^{2}} + V(x) \psi (x) = E \psi (x)$$
(3)

فیلم آموزش مکانیک کوانتومی 1 – مرور و حل تمرین در فرادرس

کلیک کنید

در اغلب مسائل، جهت ساده‌تر شدن روند محاسبات، معادله موج شرودینگر را به فرم زیر می‌نویسند. در رابطه زیر $$k$$ به عدد موج موسوم است:

$$\large \frac{\text{d}^{2} \psi ( x) }{\text{d}x^{2}} + k^{2} \psi (x) = 0$$
(4)

با توجه به دو رابطه (۳) و (۴)، دو حالت زیر برای مسئله پله پتانسیل با شرط $$E > V_{0}$$ وجود دارد:

$$\large \frac{\text{d}^{2} \psi_{1} ( x) }{\text{d}x^{2}} + k_{1}^{2} \psi_{1} (x) = 0\ \ \ ,\ \ \ k_{1}^{2} = \frac{ 2 m E }{\hbar^{2}}\ \ \ ,\ \ \ (x < 0)$$
(5)

$$\large \frac{\text{d}^{2} \psi_{2} ( x) }{\text{d}x^{2}} + k_{2}^{2} \psi_{2} (x) = 0\ \ \ ,\ \ \ k_{2}^{2} = \frac{ 2 m ( E - V_{0} ) }{\hbar^{2}}\ \ \ ,\ \ \ (x \geq 0)$$
(6)

از مباحث معادلات دیفرانسیل می‌دانیم که عمومی‌ترین پاسخ معادلات فوق، امواج تخت (plane waves) به شکل زیر هستند (مجموع دو موج تخت مستقل خطی):

$$\large \psi_{1} (x) = A e^{i k_{1} x} + B e^{-i k_{1} x}\ \ \ ,\ \ \ (x < 0)$$
(7)

$$\large \psi_{1} (x) = C e^{i k_{2} x} + D e^{-i k_{2} x}\ \ \ ,\ \ \ (x \geq 0)$$
(8)

که در آن‌ها مفهوم ضرایب به صورت زیر است:

• $$\large A e^{i k_{1} x}$$ و $$\large C e^{i k_{2} x}$$ موج‌های رونده در جهت $$x$$ ( از سمت چپ به راست)
• $$\large B e^{-i k_{1} x}$$ و $$\large D e^{-i k_{1} x}$$  موج‌های متناظر با موج رونده در خلاف جهت (منفی) $$x$$ (راست به چپ).

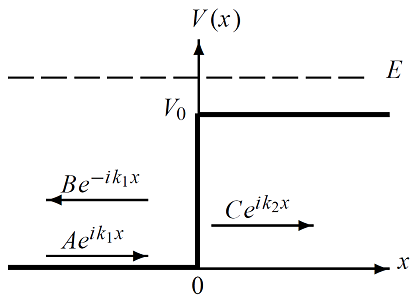
بدیهی است که در اینجا، حالتی بررسی می‌شود که ذرات ابتدا از سمت چپ به سمت پله پتانسیل می‌آیند. ذرات مذکور در نقطه‌ای که یکباره با پتانسیل $$V_{0}$$ روبه‌رو می‌شوند ($$x \geq 0$$)، می‌توانند از پله عبور یا از آن بازتابیده شوند. از آنجایی که هیچ موجی از ناحیه $$x > 0$$ به سمت چپ بازتابیده نمی‌شود (شکل 3)، بدیهی است که ثابت $$D$$ در معادله (8) باید صفر باشد. توجه داشته باشید که موج در نقطه $$x = 0$$ می‌تواند از پله بازتابیده شود و یا از آن عبور کند.

از آنجایی که با حالت‌های مانا یا ایستا (stationary states) مواجه هستیم، تابع موج کامل به صورت زیر در می‌آید:

$$\large \Psi ( x , t ) = \begin{cases}\psi_{1} (x) e^{-i \omega t} = A e^{i(k_{1} x - \omega t)} + B e^{-i(k_{1} x + \omega t)} & x < 0\\\psi_{2} (x) e^{-i \omega t} = C e^{i(k_{2} x - \omega t)} & x \geq 0\end{cases}$$
(9)

به بیانی ساده، منظور از حالت مانا یا ایستا در مکانیک کوانتومی، حالتی است که انرژی مشخصی دارد. مفهوم جملات معادله فوق به صورت زیر است. به شکل دقت (3) کنید.

• $$\large A e^{i(k_{1} x - \omega t)}$$ : موج فرودی یا برخوردی به پله پتانسیل (چپ به راست)
• $$\large B e^{-i(k_{1} x + \omega t)}$$ : موج بازتابیده از پله پتانسیل در نقطه $$x = 0$$ (راست به چپ)
• $$\large C e^{i(k_{2} x - \omega t)}$$ : موج عبوری از پله پتانسیل (چپ به راست)

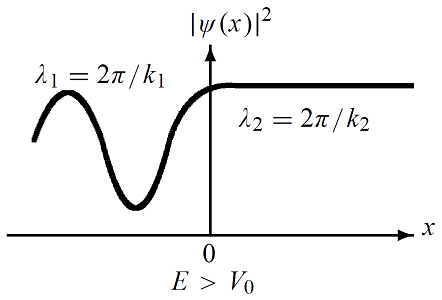
همان‌طور که می‌دانید، چگالی احتمال به صورت $$| \psi (x) |^{2}$$ تعریف می‌شود. با توجه به معادله (9)، چگالی احتمال برای ناحیه $$x > 0$$، عددی ثابت است. این امر در شکل (4) نشان داده شده است.

$$\large | \psi_{2} (x) |^{2} = | C e^{i(k_{2} x - \omega t)} |^{2} = | C |^{2}$$
(10)

حال در ادامه مطلب، ضرایب بازتاب $$R$$ و عبور $$T$$ را محاسبه می‌کنیم. ضرایب مذکور به صورت زیر تعریف می‌شوند.

$$\large R = | \frac{ Reflected\ Current\ Density }{ Incident\ Current\ Density } | = | \frac{ J_{Reflected} }{ J_{Incident} } |$$
(11)

$$\large T = | \frac{ Transmitted\ Current\ Density }{ Incident\ Current\ Density } | = | \frac{ J_{Transmitted} }{ J_{Incident} } |$$
(12)

از دو رابطه فوق، ضریب بازتاب $$R$$، نسبت باریکه بازتابیده شده به باریکه فرودی تعریف می‌شود. ضریب عبور $$T$$ نیز، نسبت باریکه عبوری به باریکه فرودی تعریف می‌شود. در اینجا لازم است تا چگالی‌های جریان $$J$$ را به دست آوریم. به طور کلی، $$J$$ چگالی جریان احتمال است که رابطه آن به صورت زیر است:

$$\large J = \frac{ i \hbar }{ 2 m } (\psi \triangledown \psi^{*} - \psi^{*} \triangledown \psi)$$
(13)

از معادله (9)، موج فرودی جمله $$A e^{i(k_{1} x - \omega t)}$$ است. در نتیجه چگالی جریان فرودی (شار فرودی یا برخوردی) با استفاده از رابطه فوق، به صورت زیر محاسبه می‌شود:

$$\large J_{Incident} = \frac{ \hbar k_{1} }{ m } | A |^{2}$$
(14)

به صورت مشابه با بالا (استفاده از معادله ۹ و 13)، می‌توانیم چگالی جریان بازتابیده ($$J_{Reflected}$$) و چگالی جریان عبوری ($$J_{Transmitted}$$) را به فرم زیر دست آوریم:

$$\large J_{Reflected} = - \frac{\hbar k_{1} }{ m } | B |^{2}$$
(15)

$$\large J_{Transmitted} = \frac{\hbar k_{2} }{ m } | C |^{2}$$
(16)

حال چگالی‌های جریان به دست آمده در بالا را به سادگی در دو رابطه (11) و (12) جایگذاری کرده و دو ضریب بازتاب $$R$$ و عبور $$T$$ را به دست می‌آوریم.

$$\large R = \frac{ | B |^{2} }{ | A |^{2} }$$
(17)

$$\large T = \frac{ k_{2} | C |^{2} }{ k_{1} | A |^{2} }$$
(18)

حال نیاز است تا با استفاده از شرایط مرزی در نقطه $$x = 0$$، ضرایب $$A$$، $$B$$ و $$C$$ را به دست آوریم. تابع موج و مشتق آن هر دو در نقطه $$x = 0$$ پیوسته هستند. یعنی:

$$\large \psi_{1} (0) = \psi_{2} (0)$$
(19)

$$\large \frac{ \text{d} \psi_{1} (0) }{ \text{d} x } = \frac{ \text{d} \psi_{2} (0) }{ \text{d} x }$$
(20)

با توجه به دو شرط مرزی فوق، از دو معادله (7) و (8) نتیجه می‌شود:

$$\large A = B + C \ \ \ \ , \ \ \ \ k_{1} ( A - B ) = k_{2} C$$
(21)

در نتیجه:

$$\large B = \frac{ k_{1} - k_{2} }{ k_{1} + k_{2} } A$$
(22)

$$\large C = \frac{ 2 k_{1} }{ k_{1} + k_{2} } A$$
(23)

از آنجایی که ضریب بازتاب $$R$$ و ضریب عبور $$T$$ به صورت نسبت بیان می‌شوند، ضریب $$A$$ از صورت و مخرج کسر ساده می‌شود و نیازی به محاسبه آن نیست. با این حال ثابت $$A$$ (مربوط به موج فرودی) از شرط بهنجارش یا نرمالیزاسیون (normalization condition) تابع موج قابل محاسبه است. با توجه به مطالب فوق داریم:

$$\large R = \frac{ (k_{1} - k_{2})^{2} }{ (k_{1} + k_{2})^{2} } = \frac{ ( 1 - \chi )^{2} }{ ( 1 + \chi )^{2} }$$
(24)

$$\large T = \frac{ 4k_{1} k_{2} }{ (k_{1} + k_{2})^{2} } = \frac{ 4 \chi }{ ( 1 + \chi )^{2} }$$
(25)

$$\large \chi = \frac{ k_{2} }{ k_{1} } = \sqrt{ 1 - V_{0}/E}$$
(26)

بدیهی است که مجموع ضریب بازتاب $$R$$ و عبوری $$T$$ باید برابر با یک باشد که با توجه به روابط فوق، این امر نیز محقق می‌شود.

تحلیل

همان‌طور که ملاحظه کردید، برخلاف رویکرد کلاسیکی که بیان می‌کند که ذرات با انرژی $$E > V_{0}$$ بازتابیده نمی‌شوند، رویکرد کوانتومی بیان می‌کند که ضریب بازتاب $$R$$ صفر نیست. به عبارت دیگر، با اینکه انرژی ذرات از انرژی پتانسیل پله بزرگتر است، بازهم احتمال دارد که ذراتی از پله پتانسیل بازتابیده شوند. این پدیده را می‌توان به رفتار موجی ذرات نسبت داد.

از ضریب عبور $$T$$ در معادله (25) نیز نتیجه می‌شود که با کم شدن انرژی $$E$$ ذرات، ضریب عبور $$T$$ نیز کوچک‌تر شده که نهایتاً به سمت صفر میل می‌کند. بدیهی است که در این صورت، ضریب بازتاب $$R$$ به سمت یک میل می‌کند.

همچنین در صورتی که انرژی ذرات بسیار بزرگ‌تر از انرژی پتانسیل پله باشد، ضریب $$\chi$$ برابر با یک شده که در نتیجه ضریب بازتاب به سمت صفر و ضریب عبور به سمت یک میل می‌کند.

مفهوم فیزیکی شرایط مرزی

در مسائل مکانیک کوانتومی غالباً نیاز به شرایط مرزی برای یافتن و تحلیل پاسخ‌های معادله موج شرودینگر داریم. سوال بسیار مهمی که در اینجا مطرح می‌شود این است که چرا از شرط پیوستگی تابع موج و مشتق آن استفاده می‌شود. مفهوم فیزیکی دو شرط مرزی مذکور، به صورت زیر است:

• چگالی احتمال $$| \psi ( x ) |^{2}$$ برای یافتن موقعیت ذره در هر ناحیه کوچکی به صورت پیوسته از نقطه‌ای به نقطه دیگر تغییر می‌کند. در نتیجه تابع موج $$\psi ( x )$$ الزاماً تابعی پیوسته از $$x$$ است. از این حیث در مسائل از شرط مرزی زیر استفاده می‌کند.

  $$\large \psi_{1} (x) = \psi_{2} (x)$$
  (27)

• عملگر یا اپراتور تکانه خطی در مکانیک کوانتومی به صورت زیر تعریف می‌شود.

  $$\large \widehat{P} \psi ( x ) = - i \hbar \frac{ \text{d} \psi ( x ) }{ \text{d} x }$$

  رابطه فوق، باید تابعی پیوسته از $$x$$، حین حرکت ذره باشد. با توجه به مشتق مکانی تابع موج در رابطه فوق، بدیهی است که مشتق تابع موج نیز باید پوسته باشد. از این حیث در مسائل از شرط مرزی زیر استفاده می‌کنند:

  $$\large \frac{ \text{d} \psi_{1} (x) }{ \text{d} x } = \frac{ \text{d} \psi_{2} (x) }{ \text{d} x }$$
  (28)

حالت $$\large E\ <\ V_{0}$$

در این بخش حالتی را در نظر می‌گیریم که انرژی $$E$$ ذرات از انرژی پتانسیل پله ($$V_{0}$$) کوچک‌تر باشد. در ادامه این مطلب با ما همراه باشید.

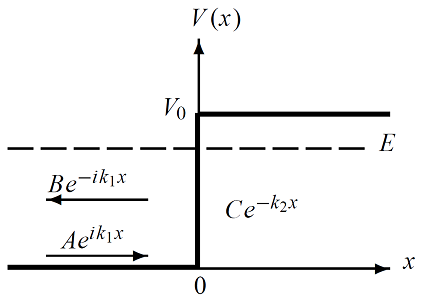
دیدگاه کلاسیکی

از نقطه نظر کلاسیکی، ذراتی که از سمت چپ با تکانه $$P = \sqrt{ 2 m E}$$، به سمت پله پتانسیل می‌آیند، به دلیل اینکه انرژی آن‌ها کمتر از انرژی پتانسیل پله است، در نقطه  $$x = 0$$ متوقف شده و بدون تغییر تکانه به سمت چپ تغییر جهت می‌دهند. به عبارت دیگر، ذرات انرژی کافی جهت عبور از پله را نداشته و به صورت کامل بازتاب می‌شوند.

دیدگاه کوانتومی

همانند حالت قبل، مکانیک کوانتومی دیدگاه متفاوتی نسبت به دیدگاه کلاسیکی دارد. در اینجا معادله شرودینگر برای ناحیه $$x < 0$$ همانند رابطه (5) نتیجه می‌شود. تابع موج برای ناحیه $$x > 0$$ به دلیل شرط $$E < V_{0}$$ متفاوت است. این دو تابع موج به شکل زیر هستند:

$$\large \frac{\text{d}^{2} \psi_{1} ( x) }{\text{d}x^{2}} + k_{1}^{2} \psi_{1} (x) = 0\ \ \ ,\ \ \ k_{1}^{2} = \frac{ 2 m E }{\hbar^{2}}\ \ \ ,\ \ \ (x < 0)$$
(29)

$$\large \frac{\text{d}^{2} \psi_{2} (x) }{\text{d}x^{2}} - k_{2}^{'2} \psi_{2} (x) = 0\ \ \ ,\ \ \ k_{2}^{'2} = \frac{ 2 m ( V_{0} - E ) }{\hbar^{2}}\ \ \ ,\ \ \ (x \geq 0)$$
(30)

در اینجا نیز پاسخ عمومی معادله موج‌ برای ناحیه $$x < 0$$ همانند بخش قبل، موج تخت (مجموع دو موج تخت مستقل خطی) است. پاسخ معادله موج $$\psi_{2} (x)$$ نیز به صورت زیر است:

$$\large \psi_{2} (x) = C e^{ - k_{2}^{'} x } + D e^{ k_{2}^{'} x }\ \ \ , \ \ \ (x \geq 0)$$
(31)

توجه داشته باشید به دلیل اینکه تابع موج باید در همه‌جا متناهی شود، با میل کردن $$x$$ به سمت بی‌نهایت، جمله $$e^{ k_{2}^{'} x }$$ واگرا می‌شود. در نتیجه ثابت $$D$$ صفر می‌شود. با این اوصاف، تابع موج توصیف کننده مسئله پله پتانسیل با شرط $$E\ <\ V_{0}$$ به صورت زیر در می‌آید:

$$\large \Psi ( x , t ) = \begin{cases}\psi_{1} (x) e^{-i \omega t} = A e^{i(k_{1} x - \omega t)} + B e^{-i(k_{1} x + \omega t)} & x < 0\\\psi_{2} (x) e^{-i \omega t} = C e^{ -k_{2}^{'} x}e^{-i \omega t} & x \geq 0\end{cases}$$
(32)

همان‌طور که ملاحظه می‌کنید، تابع موج متناظر با ناحیه $$x \geq 0$$، تابعی حقیقی است (پارامتر $$i$$ ندارد). با توجه به این امر، در ادامه خواهیم دید که چگالی جریان عبوری صفر می‌شود.

از آنجایی که چگالی جریان عبوری صفر می‌شود، ضریب عبور $$T$$ نیز صفر می‌شود. توجه داشته باشید که برای یک تابع حقیقی داریم:

$$\large real\ :\ \psi^{*} (x) = \psi (x)$$
(33)

در نتیجه چگالی جریان عبوری صفر نتیجه می‌شود:

$$\large J_{transmitted}^{'} = \frac{ i \hbar }{ 2 m } (\psi \triangledown \psi^{*} - \psi^{*} \triangledown \psi) = 0$$
(34)

با توجه به اینکه ضریب عبور صفر است، ضریب بازتاب $$R$$ باید یک شود. این امر با استفاده از شرط مرزی پیوستگی در نقطه شروع پله پتانسیل ($$x=0$$) برای دو معادله (29) و (30) قابل بررسی است. با اعمال شرط پیوستگی مذکور داریم:

$$\large B = \frac{ k_{1} - i k_{2}^{'} }{ k_{1} + i k_{2}^{'} } A$$
(35)

$$\large C = \frac{ 2 k_{1} }{ k_{1} + i k_{2}^{1} } A$$
(36)

$$\large \Rightarrow R = \frac{ | B |^{2} }{ | A |^{2} } = \frac{ k_{1}^{2} + k_{2}^{'2} }{ k_{1}^{2} + k_{2}^{'2} } = 1$$
(37)

تحلیل

همان‌طور که مشاهده می‌کنید، در اینجا نیز مانند حالت کلاسیکی، ضریب بازتاب مقدار یک شده که به معنی بازتاب کامل است. تفاوت مهمی که دیدگاه کوانتومی با دیدگاه کلاسیکی در این مسئله دارد، این است که مکانیک کوانتومی احتمال عبور ذره از پله پتانسیل را غیر صفر می‌داند. این در حالی است که از نقطه نظر مکانیک کلاسیک، ناحیه $$x > 0$$، ناحیه‌ای ممنوعه برای ذرات با انرژی $$E < V_{0}$$ است.

جهت بررسی این مطلب، چگالی احتمال را برای تابع موج عبوری به دست می‌آوریم:

$$\large P(x) = | \psi_{2} (x) |^{2} = | C |^{2} e^{ - 2 k_{2}^{'} x } = \frac{ 4 k_{1}^{2} | A |^{2} }{ k_{1}^{2} + k_{2}^{'2} } e^{ - 2 k_{2}^{'} x }$$
(38)

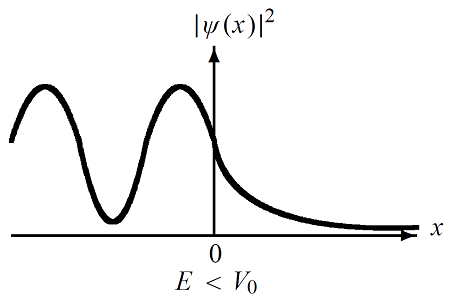
همان‌طور که ملاحظه می‌کنید، مقدار چگالی احتمال در نزدیکی نقطه $$x = 0$$ غیر صفر بوده که با افزایش $$x$$ به صورت نمایی کاهش پیدا می‌کند یا به اصطلاح میرا می‌شود. این امر در شکل (6) نیز نشان داده شده است.

علی‌رغم اینکه ضریب بازتاب، یک نتیجه شد، مکانیک کوانتومی پیش‌بینی می‌کند که ذرات با انرژی کمتر از انرژی پتانسیل پله ($$E < V_{0}$$)، احتمال دارد که به ناحیه پله نفوذ کنند و در آن‌جا میرا شوند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آموزش فیزیک مدرن با رویکرد حل مساله
• کامپیوتر کوانتومی -- به زبان ساده
• کیوبیت -- به زبان ساده
• میزر (Maser) -- به زبان ساده

^^