آشنایی کامل با مفهوم تنش — بخش دوم: حالت کلی تنش و روش‌های تحلیل آن

در بخش اول این مقاله، به توضیح تاریخچه آشنایی با تنش و مفاهیم اساسی مرتبط با این کمیت مهم پرداختیم. در این بخش، شما را با حالت کلی تنش، تحلیل تنش و معیارهای اندازه‌گیری آن آشنا خواهیم کرد.

حالت کلی تنش

اجسام مکانیکی در اغلب موارد، بیش از یک نوع تنش را به طور هم‌زمان تجربه می‌کنند. این وضعیت، با عنوان «تنش مرکب» (Combined Stress) شناخته می‌شود. مقدار حداکثری تنش‌های نرمال و برشی، در سطوح عمود بر یک راستای مشخص (d) و مقدار حداقلی این تنش‌ها (صفر) در سطوح موازی با d رخ می‌دهند.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

هنگامی که تنش برشی تنها در امتداد صفحات عمود بر یک راستای مشخص صفر شود، به تنش موجود، «تنش تک محوری» (Biaxial Sterss) گفته می‌شود. تنش تک محوری از حاصل جمع دو تنش نرمال یا برشی به دست می‌آید. به طور کلی، مقدار تنش در امتداد هیچ یک از المان‌های سطح صفر نیست و این وضعیت با عنوان «تنش سه محوری» (Triaxial Stress) شناخته می‌شود.

تانسور تنش کوشی

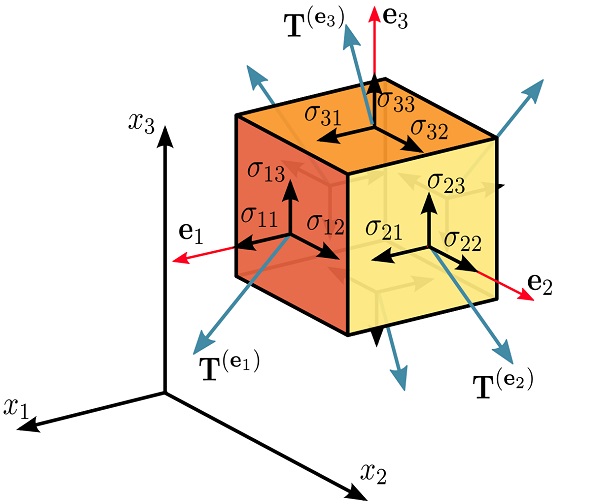
تنش‌های مرکب را نمی‌توان با استفاده از یک بردار نمایش داد. حتی اگر نحوه اعمال تنش در تمام بخش‌های درون جسم یکسان باشد نیز تنش در هر صفحه فرضی، به جهت‌گیری آن صفحه بستگی خواهد داشت. با این وجود، کوشی دریافت که بردار تنش (T) بر روی یک سطح همیشه یک تابع خطی از بردار نرمال یکه (n) آن سطح خواهد بود. به این ترتیب:

$$T={\boldsymbol {\sigma }}(n)$$

برای هر بردار u و v و هر عدد حقیقی α و β، تابع σ به صورت زیر خواهد بود:

$${\boldsymbol {\sigma }}(\alpha u+\beta v)=\alpha {\boldsymbol {\sigma }}(u)+\beta {\boldsymbol {\sigma }}(v)$$

تابع σ (تانسور تنش کوشی)، حالت کلی تنش یک جسم را به طور کامل توصیف می‌کند. در «حساب تانسوری» (Tensor Calculus)، σ به عنوان یک تانسور مرتبه دوم طبقه‌بندی شده است. تانسور تنش را می‌توان با استفاده از یک ماتریس 3*3 در هر دستگاه مختصات دکارتی دلخواه نمایش داد.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

ماتریس تنش بر اساس نحوه نام‌گذاری مختصات (x₁, x₂, x₃) یا (x, y, z)، به دو صورت زیر نوشته می‌شود:

$${\displaystyle {\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13} \\ \sigma _{21}&\sigma _{22}&\sigma _{23} \\ \sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}}$$

یا

$${\begin{bmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\ \sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\ \sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\ \end{bmatrix}}$$

بردار تنش (T=σ(n بر روی صفحه‌ای با بردار نرمال n به مختصات (n₁, n₂, n₃) برابر است با:

$$T=n\cdot {\boldsymbol {\sigma }}={\boldsymbol {\sigma }}^{T}\cdot n^{T}$$

در رابطه بالا، بالانویس «T» به معنای ترانهاده ماتریس است. به این ترتیب، داریم:

$${\begin{bmatrix}T_{1}\\T_{2}\\T_{3}\end{bmatrix}}={\begin{bmatrix}\sigma _{11}&\sigma _{21}&\sigma _{31}\\ \sigma _{12}&\sigma _{22}&\sigma _{32}\\ \sigma _{13}&\sigma _{23}&\sigma _{33}\end{bmatrix}}{\begin{bmatrix}n_{1}\\n_{2}\\n_{3}\end{bmatrix}}$$

رابطه خطی بین T و n، از قوانین بقای گشتاور خطی و تعادل استاتیکی نیروها پیروی می‌کند. از این‌رو می‌توان آن را برای هر نوع ماده و هر نوع شرایط تنش مورد استفاده قرار داد. مؤلفه‌های تانسور تنش برای تمامی نقاط جسم، در معادلات تعادل (معادلات حرکت کوشی برای شتاب صفر) صدق می‌کنند. به علاوه، بر اساس اصل بقای گشتاور زاویه‌ای، تانسور تنش دارای تقارن است. یعنی:

$$\sigma _{12}=\sigma _{21}$$

$$\sigma _{13}=\sigma _{31}$$

$$\sigma _{23}=\sigma _{32}$$

به این ترتیب، می‌توان حالت تنش نقاط یک جسم در هر لحظه از زمان را با شش پارامتر مستقل مشخص کرد:

$${\begin{bmatrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\ \tau _{xy}&\sigma _{y}&\tau _{yz}\\ \tau _{xz}&\tau _{yz}&\sigma _{z}\end{bmatrix}}$$

در ماتریس بالا، المان‌های σ_y ،σ_x و σ_z با عنوان «تنش‌های نرمال متعامد» (Orthogonal Normal Stresses) و المان‌های τ_xz، τ_xy و τ_yz نیز با عنوان «تنش‌های برشی متعامد» (Orthogonal Shear Stresses) شناخته می‌شوند.

تغییر مختصات تنش

تانسور تنش کوشی در صورت تغییر دستگاه مختصات از قانون تبدیل تانسور پیروی خواهد کرد. یکی از روش‌های نمایش گرافیکی این تبدیلات، استفاده از «دایره مور» (Mohr's Circle) است. تانسور تنش σ، دارای سه بردار ویژه (e₁, e₂, e₃) و سه مقدار ویژه (λ₁, λ₂, λ₃) است. معادله زیر، رابطه بین تنش، بردارهای ویژه و مقادیر ویژه را نشان می‌دهد:

$${\boldsymbol {\sigma }}e_{i}=\lambda _{i}e_{i}$$

تانسور تنش در یک دستگاه مختصات با محورهای منطبق بر بردارهای ویژه (e₁, e₂, e₃)، یک ماتریس قطری با سه مؤلفه نرمال (λ₁, λ₂, λ₃) است. مؤلفه‌های نرمال همان تنش‌های اصلی هستند. اگر هر سه مقدار ویژه با هم برابر باشند، تنش از نوع همسانگرد فشاری یا کششی خواهد بود. در این حالت، هیچ تنش برشی وجود نخواهد داشت. به علاوه، جهت تنش همیشه بر تمام صفحات عمود بوده و تانسور در هر دستگاه مختصات دلخواه به صورت یک ماتریس قطری خواهد بود.

تعریف تنش به عنوان یک میدان تانسور

به طور کلی، تنش درون یک جسم به صورت یکنواخت توزیع نمی‌شود و امکان تغییر آن در طی زمان وجود دارد. بنابراین، تانسور تنش باید برای نقطه مورد نظر و در لحظه مورد نظر تعریف شود. برای این کار، در ابتدا فرض می‌شود که نقطه مورد نظر توسط یک ذره کوچک احاطه شده است. سپس، میانگین تنش‌های موجود در آن ذره به عنوان تنش نقطه در نظر گرفته می‌شود.

تعریف تنش در صفحات نازک

اکثر اشیا ساخت بشر، توسط ورق‌هایی از جنس مواد مختلف و از طریق فرآیندهایی نظیر برش، حفاری، خمش ملایم و جوشکاری لبه‌ها تولید می‌شوند. این فرآیندها تغییری در ماهیت دوبعدی اجسام ایجاد نمی‌کنند. به همین دلیل برای ساده‌سازی تعریف تنش در بخش‌های ایجاد شده توسط فرآیندهای مذکور می‌توان آن‌ها را به صورت سطوح دوبعدی مدل‌سازی کرد.

با ساده‌سازی اجسام سه‌بعدی به سطوح دوبعدی، می‌توان تکه‌های بسیار کوچک هر سطح را به عنوان یک ذره در نظر گرفت. به این ترتیب، مرز بین ذرات مجاور به یک المان خط بسیار کوچک تبدیل شده و فرض می‌شود که ذرات و مرز بین آنها در راستای بعد سوم (عمود بر صفحه) گسترش یافته‌اند. در این حالت، تنش به صورت نیروهای بین دو ذره مجاور در امتداد خط مشترکشان تقسیم بر طول آن خط تعریف خواهد شد. بر اساس این تعریف، برخی از مؤلفه‌های تانسور تنش می‌توانند نادیده گرفته شود اما از آنجایی که ذرات در بعد سوم صفحه کوچک نیستند، نمی‌توان گشتاور اعمال شده از طرف یک ذره به ذره مجاور را نادیده گرفت. در این وضعیت، گشتاور جسم به صورت تنش خمشی با امکان تغییر انحنای صفحه مدل‌سازی می‌شود. با این وجود، در برخی از موارد، امکان اعمال ساده‌سازی‌های بالا به محل جوش‌ها، انحناها و چین‌های جسم وجود ندارد.

تعریف تنش در تیرهای نازک

علاوه بر ورق‌های نازک، امکان ساده‌سازی تحلیل تنش برای میله‌ها، تیرها و سیم‌هایی با ترکیب و سطح مقطع یکنواخت، تحت خمش و پیچش ملایم نیز وجود دارد. برای این اجسام می‌توان تنها سطح مقطع‌های عمود محور میله را در نظر گرفت و بخش‌های بسیار کوچک بین دو سطح مقطع را به عنوان ذره تعریف کرد. در این حالت، تنش معمولی به یک کمیت اسکالر (کشش یا تراکم میله) تبدیل می‌شود اما امکان محاسبه تنش خمشی (تغییر انحنای میله در راستای عمود بر محور) و تنش پیچشی (پیچش میله در اطراف محور) نیز وجود دارد.

تعاریف دیگر تنش

تانسور تنش کوشی برای تحلیل تنش اجسام تحت تغییر شکل‌های کوچک مورد استفاده قرار می‌گیرد. در این وضعیت، توزیع تنش در اغلب موارد قابل اغماض است. برای تحلیل تنش در تغییر شکل‌های بزرگ یا «تغییر شکل‌های محدود» (Finite Deformations)، باید از معیارهای دیگری نظیر «تانسور مرتبه اول تنش پیولا-کیرشهف» (First Piola–Kirchhoff Stress Tensor)، «تانسور مرتبه دوم تنش پیولا-کیرشهف» (Second Piola–Kirchhoff Stress Tensor)، «تانسور تنش بیو» (Biot Stress Tensor) و «تانسور تنش کیرشهف» (Kirchhoff Stress Tensor) استفاده کرد.

جامدات، مایعات و گازها دارای میدان تنش هستند. سیالات استاتیک تنش نرمال را تحمل می‌کنند اما تحت تنش برشی جریان می‌یابند. حرکت سیالات ویسکوز موجب تحمل تنش برشی در آنها می‌شود (فشار دینامیک). جامدات توانایی تحمل هر دو تنش نرمال و برشی را دارند. مواد شکل‌پذیر تحت تنش برشی و مواد شکننده تحت تنش نرمال می‌شکنند. خصوصیات مرتبط با تنش تمام مواد دارای متغیرهای وابسته به دما هستند و مواد غیر نیوتنی، متغیرهای وابسته به نرخ دارند.

تحلیل تنش

تحلیل تنش، یکی از شاخه‌های فیزیک کاربردی است که مسائل مربوط به تعیین توزیع نیروهای داخلی درون اشیا جامد را مورد بررسی می‌دهد. در علوم مهندسی، مطالعه و طراحی سازه‌هایی نظیر تونل‌ها، سدها، قطعات مکانیکی و اسکلت سازه‌ها (در حین بارگذاری مورد انتظار یا از پیش تعیین شده) با استفاده از تحلیل تنش صورت می‌گیرد.

فیلم آموزش مقاومت مصالح – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

از دیگر کاربردهای مهم این حوزه می‌توان به مطالعه مفاهیمی از قبیل صفحات تکتونیکی، آتش‌فشان‌ها و ریزش بهمن در مسائل زمین‌شناسی و درک آناتومی موجودات زنده در زیست‌شناسی اشاره کرد.

اهداف تحلیل تنش و فرضیات مورد استفاده در آن

به طور کلی، تحلیل تنش برای اشیا یا سازه‌هایی صورت می‌گیرد که بتوان آن‌ها را در حالت تعادل استاتیکی در نظر گرفت. بر اساس قانون حرکت نیوتون، هر نیروی خارجی وارد شده به چنین سیستمی، باید توسط نیروهای عکس‌العمل داخلی خنثی شود. این عکس‌العمل‌ها در اغلب موارد، نیروهای اتصال سطحی بین ذرات مجاور (همان تنش) درون ماده هستند. از آنجایی که تمام ذرات باید در حالت تعادل باشند، نیروی عکس‌العمل از ذره‌ای به ذره دیگر گسترش می‌یابد و یک توزیع تنش را درون جسم به وجود می‌آورد.

یکی از مسائل رایج در تحلیل تنش، تعیین تنش‌های داخلی بر اساس نیروهای خارجی اعمال شده به سیستم است. در مراحل بعدی تحلیل شاید موارد دیگری نیز مورد ارزیابی و محاسبه قرار گیرند؛ مثلاً «نیروهای جسمی» (Body Forces) از قبیل نیروی ثقل یا جذب مغناطیسی که درون حجم ماده عمل می‌کنند یا بارهای متمرکز از جمله اصطکاک بین محور و یاتاقان یا وزن چرخ قطار بر روی ریل که به صورت دوبعدی و در راستای یک خط یا در یک نقطه در نظر گرفته می‌شوند.

روش‌های تحلیل تنش

با اعمال بار به اجسام واقعی یا نمونه کوچک شده آن‌ها و اندازه‌گیری تنش‌های حاصل شده می‌توان تحلیل تنش را به صورت تجربی و با استفاده از چندین روش مختلف اجرا کرد. این رویکرد معمولاً برای نظارت و تأیید ایمنی مورد استفاده قرار می‌گیرد. با این وجود، تحلیل‌های تنش اغلب به وسیله روش‌های ریاضی و در حین طراحی صورت می‌گیرند.

مسائل اولیه تحلیل تنش را می‌توان با استفاده از معادله حرکت اویلر برای اجسام پیوسته (برگرفته از قوانین نیوتون در تبدیل گشتاور خطی و زاویه‌ای) و قاعده تنش کوشی-اویلر به همراه معادلات مشخصه مناسب به صورت فرمول درآورد. به این ترتیب، یک دستگاه معادلات دیفرانسیل تفاضلی متشکل از میدان تانسور تنش و میدان تانسور کرنش به دست می‌آید. این میدان‌ها، توابع مجهول دستگاه معادلات هستند که مقادیر آن‌ها باید تعیین شوند. نیروهای خارجی به صورت عبارت مستقل (در سمت راست معادله) و نیروهای متمرکز به صورت شرایط مرزی در معادلات دیفرانسیل ظاهر می‌شوند. از این‌رو، مسائل اولیه تحلیل تنش یک نوع «مسئله مقدار مرزی» (Boundary Value Problem) به حساب می‌آیند.

تحلیل تنش در سازه‌های الاستیک، بر اساس تئوری‌های الاستیسیته و کرنش بی‌نهایت کوچک صورت می‌گیرد. هنگامی که بار اعمال شده منجر به ایجاد تغییر شکل دائمی در جسم شود، باید از معادلات مشخصه پیچیده‌تری استفاده شود که امکان در نظر گرفتن فرآیندهای فیزیکی از قبیل جریان پلاستیک، شکاف، تغییر فاز و غیره در آن‌ها فراهم شده است.

سازه‌های مهندسی معمولاً به گونه‌ای طراحی می‌شوند که حداکثر تنش‌های پیش‌بینی شده در محدوده الاستیک خطی قرار می‌گیرد (تعمیم قانون هوک به محیط‌های پیوسته). این بدان معنا است که رابطه بین تنش‌های داخلی و تغییر شکل‌های ناشی از آن‌ها به صورت خطی خواهد بود. در این حالت، معادلات دیفرانسیل معرف تانسور تنش، خطی هستند و همین موضوع، مسئله را بسیار ساده‌تر می‌کند. از این‌رو، تنش در هر نقطه یک تابع خطی از میزان بارهای اعمال شده خواهد بود. در برخی از مواقع، اگر تنش‌ها به اندازه کافی کوچک باشند، می‌توان سیستم‌های غیر خطی را نیز به صورت خطی در نظر گرفت.

اگر ابعاد فیزیکی و توزیع بارهای اعمال شده به یک سازه به گونه‌ای باشد که بتوان آن را در دو یا یک بعد بررسی کرد، امکان ساده‌سازی تحلیل تنش فراهم می‌شود. به عنوان مثال، در تحلیل خرپاها می‌توان میدان تنش در هر عضو را به صورت یکنواخت و تک محوری در نظر گرفت. از این‌رو، معادلات دیفرانسیل به یک دستگاه معادله (معمولاً خطی) به همراه چندین مجهول کاهش پیدا می‌کنند. در دیگر موارد نیز امکان کاهش ابعاد مسئله از سه به دو بعد و یا قرار دادن مدل‌های ساده‌ای نظیر کشش/فشار تک محوری، برش ساده و غیره به جای تنش کلی و تانسورهای تنش وجود دارد.

با همه این تفاسیر، به منظور تحلیل مسائل دوبعدی و سه‌بعدی باید از معادله دیفرانسیل جزئی استفاده کرد. هنگامی که هندسه، معادلات مشخصه و شرایط مرزی به اندازه کافی ساده باشند، بهره‌گیری از راه حل‌های تحلیلی یا فرم بسته برای حل معادلات دیفرانسیل امکان‌پذیر خواهد بود. در غیر این صورت، معمولاً باید روش‌های عددی از قبیل «روش المان محدود» (Finite Element Method) یا «FEM»، «روش تفاضل محدود» (Finite Difference Method) یا «FDM» و «روش المان مرزی» (Boundary Element Method) یا «BEM» را به کار گرفت.

معیارهای اندازه‌گیری تنش

در این بخش، به توضیح تانسورهای مرتبه اول و دوم تنش پیولا-کیرشهف، به عنوان معیارهای پرکاربرد در اندازه‌گیری تنش می‌پردازیم.

فیلم آموزش مقاومت مصالح 1 و 2 – مرور و حل مساله در فرادرس

کلیک کنید

تانسور تنش پیولا-کیرشهف

در تغییر شکل‌های محدود، امکان بهره‌گیری از تانسور تنش پیولا-کیرشهف برای بیان تنش در پیکربندی مرجع وجود دارد. در صورتی که برای بیان وضعیت تنش در پیکربندی فعلی، از تانسور تنش کوشی استفاده می‌شود. در تغییر شکل‌های بی‌نهایت کوچک، تانسورهای کوشی و پیولا-کیرشهف با هم یکسان هستند.

تانسور تنش کوشی (σ) با تنش‌های موجود در پیکربندی فعلی ارتباط دارد؛ در حالی که تانسورهای کرنش و گرادیان تغییر شکل با ارتباط دادن حرکت به پیکربندی مرجع توصیف می‌شوند. بنابراین، تمام تانسورهای معرف وضعیت ماده، در پیکربندی مرجع یا فعلی قرار ندارند. تعریف تنش، کرنش و تغییر شکل در یکی از این پیکربندی‌ها می‌تواند تعریف «مدل‌های ساختاری» (Constitutive Models) را ساده‌تر کند. تانسور مرتبه اول تنش پیولا-کیرشهف (P)، یکی از روش‌های ایجاد مدل‌های ساختاری است. این تانسور، مجموعه‌ای از تانسورهای معرف پیکربندی جسم در یکی از وضعیت‌های مرجع یا فعلی را تعریف می‌کند.

تانسور مرتبه اول تنش پیولا-کیرشهف، رابطه بین نیروهای موجود در پیکربندی فعلی و مساحت‌های پیکربندی مرجع را نشان می‌دهد:

$${\boldsymbol {P}}=J~{\boldsymbol {\sigma }}~{\boldsymbol {F}}^{-T}~$$

F: گرادیان تغییر شکل؛ J: دترمینان ژاکوبی J=det(F)

اگر مؤلفه‌ها را نسبت به یک پایه متعامد یکه در نظر بگیریم، خواهیم داشت:

$$P_{iL}=J~\sigma _{ik}~F_{Lk}^{-1}=J~\sigma _{ik}~{\cfrac {\partial X_{L}}{\partial x_{k}}}$$

از آن جایی که تانسور مرتبه اول تنش پیولا-کیرشهف، دستگاه‌های مختصات مختلف را به هم مرتبط می‌کند، یک تانسور دونقطه‌ای و عموماً نامتقارن به حساب می‌آید. این تانسور، تعمیم سه‌بعدی مفهوم تنش مهندسی است.

در صورتی که ماده بدون هیچ تغییری در حالت تنش تحت چرخش قرار گیرد (چرخش صلب)، مؤلفه‌های تانسور مرتبه اول تنش پیولا-کیرشهف با توجه به جهت ماده تغییر خواهند کرد. به علاوه، این تانسور «مزدوج انرژی» (Energy Conjugate) گرادیان تغییر شکل است.

تانسور مرتبه دوم تنش پیولا-کیرشهف

تانسور مرتبه اول تنش پیولا-کیرشهف رابطه بین نیروهای موجود در پیکربندی فعلی و مساحت‌ها در پیکربندی مرجع را نشان می‌دهد؛ در حالی که تانسور مرتبه دوم تنش پیولا-کیرشهف (S)، رابطه بین نیروهای موجود در پیکربندی مرجع و مساحت‌ها در همین پیکربندی را تعیین می‌کند. نیروی موجود در پیکربندی مرجع از طریق رابطه نسبی بین جهت نیرو و بردار نرمال سطح به دست می‌آید.

$${\boldsymbol {S}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}$$

اگر معادله بالا را نسبت به یک پایه متعامد یکه علامت‌گذاری کنیم، خواهیم داشت:

$$S_{IL}=J~F_{Ik}^{-1}~F_{Lm}^{-1}~\sigma _{km}=J~{\cfrac {\partial X_{I}}{\partial x_{k}}}~{\cfrac {\partial X_{L}}{\partial x_{m}}}~\sigma _{km}$$

تانسور بالا به صورت تک نقطه‌ای و متقارن است. در صورتی که ماده بدون هیچ تغییری در حالت تنش تحت چرخش قرار گیرد (چرخش صلب)، مؤلفه‌های تانسور مرتبه دوم تنش پیولا-کیرشهف ثابت باقی خواهند ماند. به علاوه، این تانسور مزدوج انرژی تانسور کشش محدود گرین-لاگرانژ است.

امیدواریم این مقاله برایتان مفید واقع شده باشد. اگر به مطالعه و یادگیری موضوعات مشابه علاقه‌مند هستید، آموزش‌های زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش های مهندسی عمران
• آموزش مقاومت مصالح
• مجموعه آموزش‌های دروس مهندسی مکانیک
• مفهوم تنش و کرنش — آشنایی با مفاهیم مقاومت مصالح
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد

^^