درخت در گراف – به زبان ساده
در آموزشهای قبلی مجله فرادرس درباره تعاریف و انواع گراف بحث شد. در این آموزش قصد داریم مفهوم درخت در گراف را بررسی کنیم. درخت یکی از مفاهیم اصلی در گراف است که در این آموزش مورد بررسی قرار میگیرد. اگر با برخی اصطلاحات این آموزش آشنا نیستید، به آموزش «گراف — تعاریف و انواع به زبان ساده» مراجعه کنید.

ابتدا یک قضیه اساسی در نظریه گراف را بیان میکنیم.
قضیه ۱
اگر یک گراف ساده با رأس و مولفه و یال باشد، گزاره زیر صحیح است:
تعریف پل در گراف
پل (Bridge) به یالی گفته میشود که در صورت حذف آن، گراف دقیقا به دو قسمت یا مولفه (Component) تبدیل میشود. در گراف همبند، قطع یالِ پل، باعث غیر همبند شدن گراف میشود.
تعریف درخت در گراف
به گرافِ همبند (متصل) و بدون دور، درخت گفته میشود. برای مثال در شکلهای زیر انواعی از درختها نشان داده شده است:
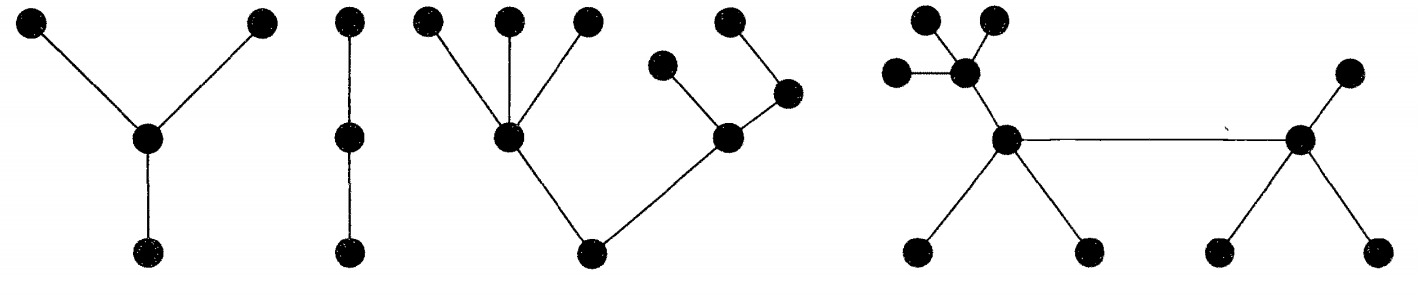
همانطور که در آموزشهای قبلی گفتیم، گرافِ بدیهی، گرافی است که تنها یک رأس دارد و هیچ یالی ندارد. درخت، سادهترین نوع گراف غیر بدیهی است. این نوع گراف، خواص جالبی دارد. برای مثال، در درخت، هر دو رأس با یک مسیر مشخص به هم متصل هستند. برای اثبات قضایای مربوط به گراف، بعضی اوقات معمول است که آن را برای درختها اثبات کنیم. در حقیقت، معلوم شده است بسیاری از حدسهایی که برای گرافهای دلخواه ثابت نشدهاند، برای درختها صحیح هستند.
به رئوس درخت با درجه یک، برگ یا رئوس آویزان گفته میشود. بنابراین با این تعاریف، گراف ستاره یک درخت است. به یالهای یک درخت، شاخه گفته میشود. هر رأسِ درخت، یک گره نام دارد. هر درخت حداقل دو رأس با درجه یک دارد.
قضیه زیر خواص ساده درختها را نشان میدهد:
قضیه ۲
اگر یک گراف با رأس باشد، گزارههای زیر معادل هستند:
- T یک درخت است.
- T یک گراف بدون دور است و یال دارد.
- T همبند است و یال دارد.
- T همبند است و هر یال، یک پل است.
- هر دو رأس T فقط با یک مسیر به یکدیگر متصل هستند.
- T بدون دور است، اما اضافه کردن یک یال جدید، دقیقا یک دور در گراف ایجاد میکند.
اثبات: اگر باشد، تمامی این شش گزاره بدیهی هستند. بنابراین فرض میشود که .
اثبات معادل بودن گزاره های ۱ و ۲: از آنجا که هیچ دوری ندارد، حذف هر یال، موجب میشود گراف به دو گراف، تقسیم شود. هر یک از این دو گراف نیز درخت هستند. اگر به حذف یالها همچنان ادامه دهیم به طوری که مولفهها نیز درخت باقی بمانند، در نهایت به یک درخت با ۲ رأس و یک یال میرسیم. بنابراین طبق استقرا میتوان گفت تعداد یالها در هر یک از این درختها از تعداد راسها یکی کمتر است. پس میتوان نتیجه گرفت تعداد کل یالهای درخت برابر است.
اثبات معادل بودن گزارههای 2 و 3: اگر T ناهمبند باشد، هریک از مولفههای یک گراف همبند بدون دور است. بنابراین مثل حالت قبل، تعداد رئوس در هر یک از این مولفهها از تعداد یالها به اندازه ۱ عدد بزرگتر است. بنابراین کل رئوس از کل یالها در گراف ، حداقل ۲ عدد بیشتر خواهد بود. این مسئله با این قانون که گراف ، یال دارد، در تناقض است. برای مثال، شکل زیر را در نظر بگیرید.
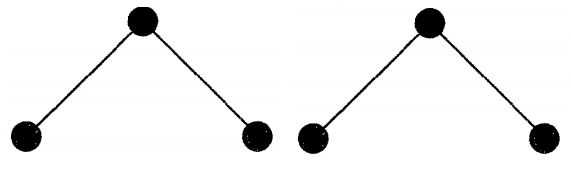
در این شکل فرض شده است یک گراف ناهمبند داریم که شامل دو گراف همبند غیر مدور است. همانطور که مشاهده میشود این گراف ۶ رأس و ۴ یال () دارد که با تعریف درخت تناقض دارد.
اثبات معادل بودن گزارههای ۳ و ۴: حذف هر یال باعث میشود گراف راس و یال داشته باشد. به این ترتیب طبق گزاره ۲، گراف ناهمبند میشود که با فرض اولیه در تناقض است.
اثبات معادل بودن گزارههای ۴ و ۵: از آنجا که یک گراف همبند است، هر جفت رأس به وسیله حداقل یک یال یا مسیر به یکدیگر متصل شدهاند. اگر یک جفت رأس با دو مسیر به هم وصل باشند، یک دور در گراف ایجاد میشود. این مورد با این قانون که هر یال یک پل است در تناقض است.
اثبات معادل بودن گزارههای ۵ و ۶: اگر شامل یک دور باشد، پس هر دو رأس در این دور با حداقل دو مسیر به یکدیگر متصل هستند که با گزاره ۵ در تناقض است. اگر یک یال به درخت اضافه شود، از آنجا که رئوسی که یال به آنها متصل است از قبل به هم وصل بودهاند، یک دور ایجاد میشود. پس فقط و فقط یک دور داریم.
اثبات معادل بودن گزارههای ۶ و ۱: فرض کنید که یک گراف ناهمبند باشد. اگر به ، یک یال اضافه کنیم که یک راس از یک مولفه را به یک راس از مولفه دیگر متصل کند، هیچ دوری ایجاد نمیشود. پس درخت، یک گراف همبند بدون دور است.
در ادامه به بیان چند مثال برای گرافها میپردازیم.
مثال ۱
گراف نشان داده شده در شکل زیر یک درخت است، زیرا هیچ دوری ندارد و همبند است. این گراف، ۴ رأس و ۳ یال دارد که با تعریف سازگار است.

مثال ۲
شکل زیر را در نظر بگیرید. در این شکل، رئوس و از درجه یک هستند. دو رأس دیگر یعنی و نیز از درجه دو هستند. به این دلیل که در درخت دور وجود ندارد، بنابراین حداقل دو یال تکی در گراف وجود دارد. این دو یال به دو رأس از درجه یک متصل هستند.
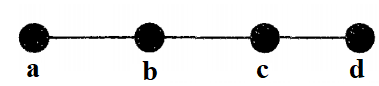
تعریف جنگل
جنگل به مجموعهای از درختها گفته میشود که به هم متصل نیستند. بنابراین مجموعهای از درختهای ناهمبند، جنگل نام دارد. در جنگل نیز مانند درخت، حلقه وجود ندارد. در تعریف کلیتر میتوان گفت که یک گراف بدون دور، جنگل است.
مثلا شکل ۱، یک جنگل با ۴ مولفه را نشان میدهد. باید اشاره کرد که درخت و جنگل، گرافهای ساده هستند. یعنی در آنها، حلقه و یال موازی وجود ندارد.
نکته
اگر G یک جنگل با راس و مولفه باشد، پس به اندازه یال دارد.
اثبات: هر یک از گزارههای قضیه ۲ را به هر یک از مولفههای گراف G اعمال کنید.
به راحتی میتوان مشاهده کرد که اگر یک جنگل یک مولفه داشته باشد، به یک درخت تبدیل میشود و طبق تبصره بالا، یال دارد که یک گزاره صحیح است.
درخت پوشا
گراف همبند و یک دور از این گراف را در نظر بگیرید. تعدادی از یالهای این دور از گراف را به گونهای حذف میکنیم که گراف همچنان همبند باقی بماند. فرض کنید حذف دورها را آنقدر ادامه دهیم تا دیگر دوری باقی نماند. گرافی که باقی میماند یک درخت است که در آن، تمامی رأسها به هم متصل هستند. به این درخت، درخت پوشای گراف گفته میشود. تعریف سادهتر درخت پوشا به این صورت است:
اگر یک گراف همبند باشد، زیرگراف از یک درخت پوشا نامیده میشود، اگر:
- یک درخت باشد.
- شامل همه رئوس باشد.
در شکل زیر یک گراف و یکی از درختهای پوشای آن نشان داده شده است:
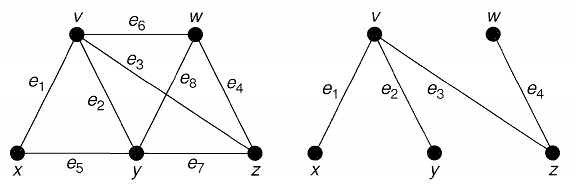
همانطور که مشاهده مشکنیم، این درخت همه رئوس گراف اصلی را شامل میشود و تعداد یالهای آن، یکی کمتر از تعداد رئوس آن است. پس این درخت، یک درخت پوشای گراف است.
در نتیجه، یک درخت پوشا از گراف بدون جهت ، زیرگرافی است که همه رئوس را شامل میشود.
درجه مدار
فرض کنید یک گراف همبند با رأس و یال باشد. درخت پوشای از گراف شامل یال است. بنابراین تعداد یالهایی که لازم است از گراف حذف کنیم تا به یک درخت پوشای بدون حلقه برسیم عبارت است از : . این عدد، درجه مداری گراف نامیده میشود.
مثال ۳
در یک گراف تعداد یالها برابر ۷ و تعداد رئوس برابر با ۵ است. درجه مداری این گراف عبارت است از:
مثال ۴
اگر یک گراف همبند با ۶ رأس و درجه هر رأس ۳ باشد، درجه مداری را بیابید.
حل: با استفاده از قضیه مجموع مرتبههای رئوس خواهیم داشت:
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره سایر موضوعات مربوط به ریاضیات مطالب بیشتری یاد بگیرید، آموزشهای زیر به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- مجموعه آموزشی جامع ریاضی دبیرستان – علوم تجربی
- آموزش نظریه گراف و کاربردها
- نظریه گراف (Graph Theory) در علوم کامپیوتر – به زبان ساده
- برهان خلف — به زبان ساده
^^












سلام برای بدست آوردن تعداد مسیر های (مثلا سه تایی) در یک گراف درختی باید چیکار کرد!؟
ممنون میشم راهنمایی کنین🙏🙏🙏