۱۵ الگوریتم ساده با جواب و توضیح راه حل

الگوریتم ساده به معنی این است که برای مسائل کوچک و معمولی، راه حل ساده و تکرارپذیر پیدا کنیم. یعنی اینکه این راه حل برای حل تمام مسائل مشابه با داده‌های متفاوت، معتبر باشد. برای نمونه، فرض کنید به منظور محاسبه مساحت مربع، راه حلی را ارائه کرده‌ایم که با کمک آن می‌توان مساحت تمام مربع‌های مختلف را بدست آورد. استفاده از الگوریتم‌های ساده با جواب، بهترین روش برای شروع مهارت طراحی و نوشتن الگوریتم‌ها است. با هدف آموزش و درک روش طراحی و نوشتن الگوریتم‌، در این مطلب تلاش کردیم که مسائل کوچکی را به صورت کلی بیان کرده و برای حل هر کدام، الگوریتم مناسبی را به شکل ساده طراحی کنیم.

در این مطلب از مجله فرادرس به بررسی ۱۵ الگوریتم ساده با جواب و توضیح راه حل پرداخته‌ایم. ابتدا روش نوشتن الگوریتم ساده را به صورت مختصر و مفید تعریف کرده و ویژگی‌‌های طراحی الگوریتم را به صورت کلی بیان کردیم. سپس ۱۵ مورد مسئله ساده را یک به یک مطرح کرده و جواب الگوریتمی هر کدام را همراه با توضیح واضحی ارائه داده‌ایم.

روش نوشتن الگوریتم ساده چیست؟

برای نوشتن الگوریتم اول از همه باید مسئله داده شده را درک کرد. سپس راه حل مورد نظر را طوری طراحی می‌کنیم که قابل بیان با زبان انسان باشد. در نتیجه این‌کار، هر برنامه نویسی می‌تواند با هر زبان برنامه نویسی دلخواه خود، الگوریتم طراحی شده را کدنویسی کند. الگوریتم‌ها دستورالعمل حل مسائل و انجام کار هستند. نوشتن الگوریتم حتما باید شامل شرایط و ویژگی‌‌های ضروری باشد که در فهرست زیر بیان کرده‌ایم.

• هر الگوریتمی باید تعداد مراحل و زمان اجرای تمام شدنی داشته باشد.
• حداقل یک خروجی تولید کند.
• قطعی باشد. یعنی نتیجه تولید شده همخوانی دقیقی با سناریو وارد شده به مسئله داشته باشد.
• هر مرحله اجرای کار در الگوریتم باید کارآمد و بهینه باشد. در واقع در هر مرحله، نتیجه خاصی باید تولید شود.

الگوریتم باید به صورت رشته‌ای از کارها طراحی شود که روش حل گروهی از مسائل را به دقت نشان می‌دهند. طراحی الگوریتم مهم‌ترین قسمت در رسیدن به راه‌ حلی موثر و کارآمد برای هر مسئله است. برای اینکه در این تکنیک از علوم کامپیوتر به خوبی مهارت پیدا کنید، پیشنهاد می‌کنیم که فیلم آموزش طراحی الگوریتم همراه با حل مثال های عملی را از فرادرس مشاهده کنید. لینک مربوط به این فیلم را در پایین نیز قرار داده‌ایم.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

۱۵ الگوریتم ساده با جواب

در این بخش از مطلب، ابتدا ۱۵ مسئله ساده را مطرح کرده‌ایم. سپس به ازای تمام این مسائل، الگوریتم جواب را طوری نوشته‌ایم که با تغییر داده‌های مسئله همواره به شکل صحیحی کار کند.

مسائل مطرح شده در این بخش را در فهرست زیر، معرفی کرده‌ایم.

1. محاسبه مساحت مربع
2. محاسبه محیط مستطیل
3. محاسبه مساحت دایره
4. تشخیص زوج یا فرد بودن اعداد
5. جمع دو عدد با یکدیگر
6. تشخیص عدد بزرگتر از بین دو عدد مجزا
7. محاسبه مساحت مثلث
8. شمارش نزولی عدد مشخص شده
9. کشف کوچکترین عضو در بین سه عدد
10. محاسبه مجموعه اعداد از ۱ تا N
11. بررسی مثبت یا منفی بودن عدد داده شده
12. معکوس کردن کلمه داده شده
13. بررسی بخش‌پذیر بودن یک عدد به عدد دیگر
14. محاسبه مقدار میانگین سه عدد مجزا
15. محاسبه تعداد روز‌ها در چندین هفته مختلف

در ادامه مطلب، الگوریتم مورد نیاز برای حل تمام مسائل بالا را یک به یک توضیح داده‌ایم. برای مطالبی که شاید فرایند کدنویسی کمی پیچیده‌تری داشته باشند، کدهای مربوطه را به زبان پایتون نیز نوشته‌ایم.

۱. الگوریتم محاسبه مساحت مربع

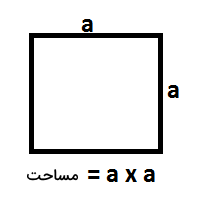
در این مسئله باید الگوریتمی بنویسیم که مساحت مربع را محاسبه کند. برای محاسبه مساحت مربع داشتن اندازه یک ضلع کافی است. فرمول مساحت مربع برابر است با اندازه ضلع ضرب در خودش.

فیلم آموزش محاسبه مساحت مربع (رایگان) در فرادرس

کلیک کنید

در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. ابتدا اندازه یک ضلع را در ورودی گرفته و برابر با a  قرار می‌دهیم.
2. عملیات محاسبه مساحت a * a  را انجام می‌دهیم.
3. نتیجه را به صورت مستقیم به خروجی برمی‌گردانیم.

۲. الگوریتم محاسبه محیط مستطیل

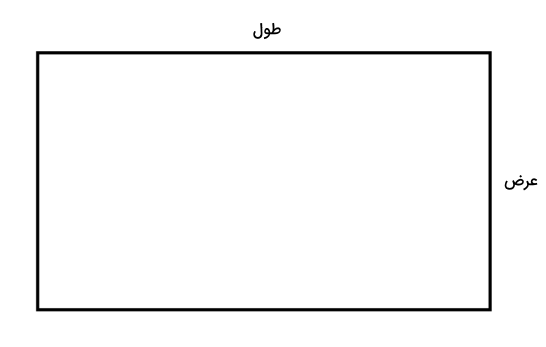
در این مسئله باید الگوریتمی برای محاسبه محیط مستطیل بنویسیم. برای محاسبه محیط مستطیل باید اندازه دو ضلع مجاور هم - طول و عرض - را داشته باشیم. بنابراین اندازه‌ این ضلع‌ها را در ورودی دریافت می‌کنیم. فرمول محاسبه محیط مستطیل برابر است با جمع اضلاع مجاور ضرب در ۲.

در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. ابتدا با نمایش پیغام مناسبی به کاربر، از ورودی، طول length  و عرض width  مستطیل را دریافت می‌کنیم.
2. عملیات جمع را بر روی طول و عرض با فرمول (length + width)  انجام می‌دهیم.
3. نتیجه حاصل از جمع طول و عرض را ضرب در عدد ۲ می‌کنیم.
4. حاصل ضرب بدست آمده را به عنوان خروجی الگوریتم به بیرون برمی‌گردانیم.

توجه: طول و عرض مستطیل همان دو ضلع مجاور هم هستند. در صورتی برابری طول و عرض با یکدیگر، محیط مربع محاسبه می‌شود. بنابراین این فرمول برای محاسبه محیط شکل مربع نیز قابل اجرا هست.

مهارت های کاربردی کامپیوتر مخصوص نوجوانان

در دنیای رو به پیشرفت آینده، یادگیری مفاهیم و مهارت‌های کامپیوتر به جزء جدایی ناپذیری از زندگی همه افراد به‌خصوص نوجوانان تبدیل می‌شود. حتی امروز هم تقریبا اکثر نوجوانان برای انجام تکالیف مدرسه، پروژه‌های تحصیلی، برقراری ارتباطات و غیره نیاز به کامپیوتر پیدا کرده‌اند. مهارت در استفاده از نرم‌افزارهای واژه‌پردازی و صفحه‌آرایی متن، توانایی کار با نرم‌افزارهای جدول گسترده مانند Microsoft Excel، استفاده از موتورهای جستجو، حفاظت از اطلاعات شخصی، ویرایش تصاویر و ویدئوها از جمله مهارت‌هایی هستند که نه تنها به نوجوانان برای انجام کارهای روزانه‌شان کمک می‌کنند، بلکه آنان را برای انتخاب بهتر شغل در آینده نیز آماده می‌کنند.

از آنجا که یادگیری مهارت‌های کامپیوتر در بسیاری از مشاغل عمومی و تخصصی مانند امور اداری، حسابداری، برنامه‌نویسی، طراحی گرافیک، و غیره لازم و ضروری است. فرادرس تلاش کرده که فیلم‌های آموزشی مناسبی را برای نوجوانان طراحی و منتشر کند. در این فیلم‌ها انواع مهارت‌های کاربردی کامپیوتر تدریس شده‌اند. از مهارت‌های کلی مانند تایپت ده‌انگشتی گرفته تا مهارت‌های تخصصی‌تری مانند آموزش محافظت از اطلاعات شخصی در ویندوز و اینترنت. در پایین چند مورد از این مهارت‌ها را معرفی کرده‌ایم.

• فیلم آموزش تایپ ده انگشتی فارسی و انگلیسی در فرادرس
• فیلم آموزش پاورپوینت Microsoft PowerPoint 2016‎ در فرادرس
• فیلم آموزش ویندوز ۱۰ Windows همراه با نکات کاربردی در فرادرس
• فیلم آموزش مهارت های هفت گانه کامپیوتر ICDL ویژه کودکان در فرادرس

با کلیک بر روی تصویر بالا به صفحه اصلی این مجموعه آموزش رفته و از فیلم‌های آموزشی بیشتری دیدن کنید.

۳. محاسبه مساحت دایره

در این مسئله باید الگوریتمی بنویسیم که مساحت دایره را محاسبه کند. برای محاسبه مساحت دایره داشتن اندازه شعاع دایره شرط لازم و کافی است. فرمول محاسبه مساحت دایره برابر است با شعاع ضرب در خودش ضرب در عدد پی «۳٫۱۴».

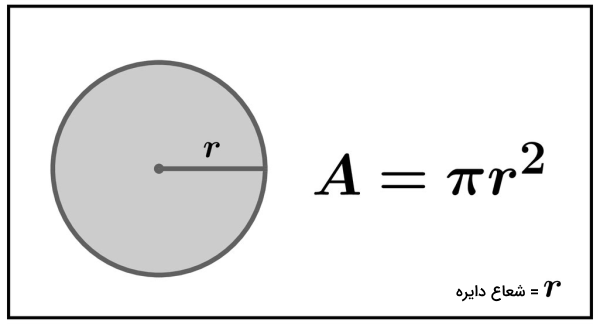
در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. ابتدا باید اندازه شعاع radius  را در ورودی از کاربر بگیریم.
2. سپس مقدار شعاع ضرب در خودش یا شعاع به توان دو را با فرمول radius * radius  محاسبه می‌کنیم.
3. نتیجه بدست آمده از مرحله قبل را در عدد3.14 - که همان مقدار عدد پی است - ضرب می‌کنیم.
4. در نهایت حاصل ضرب محاسبه شده را به عنوان جواب نهایی الگوریتم به بیرون از مسئله برمی‌گردانیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

توجه: در مرحله اول الگوریتم، حتما باید از پیغام واضحی استفاده کنیم. در صورتی که داده ورودی به الگوریتم به جای اندازه شعاع، حاوی اندازه قطر دایره باشد، نتیجه محاسبه شده کاملا غلط می‌شود.

۴. تشخیص زوج یا فرد بودن اعداد

در این مسئله باید الگوریتمی بنویسیم که زوج یا فرد بودن عدد داده شده را تشخیص دهد. برای تشخیص زوج یا فرد بودن اعداد باید از عملگر باقی‌مانده تقسیم یا بخش‌پذیری بر دو، استفاده کنیم. فرمول مورد استفاده به این صورت است که ابتدا عدد را بر دو تقسیم می‌کنیم. هر عددی که باقیمانده تقسیم آن بر عدد دو صفر بود، زوج و در غیر این صورت فرد است.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. در ابتدا عدد مورد نظر را از ورودی دریافت کرده و در متغیری با نام دلخواه number  قرار می‌دهیم.
2. مقدار باقیمانده عدد number  را بر 2  محاسبه کرده و برابری آن را با 0  بررسی می‌کنیم. این عملیات را با استفاده از فرمول number % 2 == 0 انجام می‌دهیم.
3. نتیجه عملیات مقایسه قبل را بررسی می‌کنیم.
4. اگر این نتیجه برابر با صفر بود در خروجی کلمه Even  یا زوج را برمی‌گردانیم.
5. در غیر این صورت عدد فرد است و در خروجی کلمه Odd  یا فرد را برمی‌گردانیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

۵. جمع دو عدد با یکدیگر

در این قسمت می‌خواهیم الگوریتم ساده با جواب مسئله‌ای را بنویسیم که حاصل جمع دو عدد مختلف را با یکدیگر محاسبه کند. برای محاسبه جمع دو عدد با یکدیگر باید دو ورودی مجزا از هم را به نوبت دریافت کنیم.

در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. ابتدا در ورودی دو مقدار مختلف را به صورت جدا از هم دریافت کرده و در متغیرهای number1  و number2  قرار می‌دهیم.
2. بعد با فرمول number1 + number2  نتیجه این مسئله را بدست می‌آوریم.
3. در نهایت حاصل جمع را به عنوان خروجی به بیرون برمی‌گردانیم.

روش نوشتن الگوریتم برنامه نویسی به این شکل است که قبل از نوشتن کدهای برنامه‌ - در هر زبان دلخواهی - معمولا الگوریتم‌ها را مرحله‌به‌مرحله طراحی کرده و سپس به صورت شبه کد پیاده می‌کنند. همین‌طور که مشاهده می‌کنید، در این مطلب هم روش نوشتن شبه کد الگوریتم ساده با جواب را برای ۱۵ مسئله مختلف نمایش داده‌ایم. اما در صورت نیاز به آشنایی بیشتر با روش نوشتن الگوریتم، پیشنهاد می‌کنیم که مطلب نحوه نوشتن الگوریتم برنامه نویسی، از صفر تا صد را از مجله فرادرس مطالعه کنید.

۶. تشخیص عدد بزرگتر از بین دو عدد مجزا

در این مسئله باید الگوریتمی بنویسیم که عدد بزرگتر از بین دو عدد مجزا را تشخیص دهد. برای محاسبه عدد بزرگتر از بین دو عدد مختلف، ابتدا باید این دو عدد را دریافت کرده و سپس عملگرهای مقایسه‌ای و عبارت‌های شرطی را به کار ببریم.

در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. ابتدا هر دو عدد را از ورودی دریافت کرده و در متغیرهای number1  و number2  قرار می‌دهیم.
2. سپس عبارت مقایسه‌ای number1 > number2  را به صورت شرط، بررسی می‌کنیم.
3. اگر این شرط برقرار بود پس number1  عدد بزرگتر است. در نتیجه باید آن را در خروجی برگردانیم و عملیات به پایان می‌رسد.
4. اما اگر این شرط برقرار نبود، پس یا number2  بزرگ‌تر است یا هر دو عدد با هم برابر هستند. در هر دو صورت می‌توانیم number2  را در خروجی برگردانیم تا کار الگوریتم به پایان برسد.

توجه: برای کشف بزرگترین عدد از بین چند عدد مختلف هم از همین الگوریتم استفاده می‌کنیم. فقط باید اعداد را از ابتدا به صورت دو‌به‌دو با یکدیگر مقایسه کنیم. بعد از هر مقایسه، عدد بزرگتر بدست آمده را با عدد بعد در مجموعه به همین طریق مقایسه می‌کنیم. در هر بار مقایسه فقط عدد بزرگتر انتخاب می‌شود. این عملیات تا مقایسه شدن تمامی اعداد و کشف بزرگ‌ترین عدد، ادامه خواهد داشت.

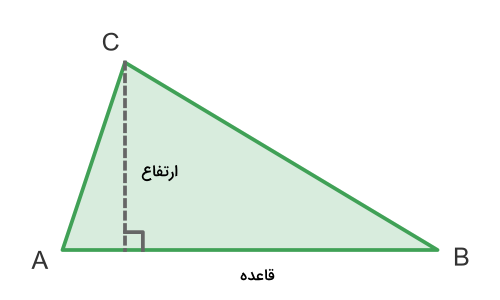
۷. الگوریتم محاسبه مساحت مثلث

در این قسمت از مطلب، باید الگوریتم ساده با جواب را برای مسئله‌ای محاسبه مساحت مثلث بنویسیم. برای توضیح الگوریتم این مسئله باید توجه کنیم که فرمول محاسبه مساحت مثلث نیازمند داشتن اندازه ارتفاع و قائده است.

در پایین الگوریتم مورد استفاده برای این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. در ابتدا باید هر دو مقدار ارتفاع و قاعده مثلث را از ورودی دریافت کنیم و به ترتیب در متغیر‌های height  و base  قرار دهیم.
2. سپس حاصل ضرب این متغیرها را با فرمول (base * height)  محاسبه می‌کنیم.
3. حاصل ضرب بدست آمده را باید تقسیم بر 2  کنیم.
4. در نهایت، نتیجه تقسیم برابر با مساحت مثلث است. جواب را در خروجی برمی‌گردانیم.

توجه: چون ارتفاع و قاعده را در یکدیگر ضرب می‌کنیم، پس اشتباه در ترتیب آن‌‌ها تاثیری منفی بر نتیجه نهایی ندارد. اما برای کدنویسی الگوریتم همیشه بهتر است که از پیغام‌ها صحیح و واضحی در برنامه استفاده کنیم. با این‌کار مقادیر درست را دریافت کرده و در متغیرهای مناسب ذخیره می‌کنیم.

۸. شمارش نزولی عدد مشخص شده

در این مسئله باید الگوریتمی بنویسیم که ابتدا عدد خاصی را دریافت کند. سپس از روی آن عدد تا مقدار 0  را به ترتیب از بالا به پایین شمرده و هر مقدار را در خروجی نمایش دهد. خروجی این الگوریتم زنجیره شمارش معکوسی از عدد داده شده تا صفر است. برای حل این مسئله باید از ساختارهای حلقه استفاده کنیم.

در پایین الگوریتم ساده با جواب مورد استفاده برای این مسئله را مرحله‌به‌مرحله بیان کرده‌ایم.

1. ابتدا عدد مورد نظر خود را از ورودی دریافت کرده و در متغیر startNumber  قرار می‌دهیم.
2. سپس حلقه‌ را طوری تعریف می‌کنیم که فقط در زمان مساوی بودن startNumber با 0 از حرکت به‌ایستد. یعنی اینکه اگر شرط startNumber == 0 برقرار باشد.
3. دستورات داخل حلقه را به این شکل می‌نویسیم که:
   1. ابتدا مقدار startNumber  را چاپ کند.
   2. سپس از startNumber  به اندازه 1  واحد کم کند.
4. دستورات درون حلقه یا مرحله ۳ را تا زمان به صفر رسیدن startNumber  ادامه می‌دهیم.
5. وقتی که startNumber  برابر با 0  شد، کار الگوریتم به پایان رسیده و می‌توانیم پیغام Done!  را در خروجی چاپ کنیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

با فرض اینکه در ورودی کد بالا، عدد 5 را وارد کنیم، خروجی زیر در کنسول پایتون نمایش داده می‌شود.

Enter the starting number: 
5
5
4
3
2
1
Done!

۹. الگوریتم کشف کوچکترین عدد در بین سه عدد

در این مسئله می‌خواهیم که برای پیدا کردن کوچکترین عدد در بین سه عدد مجزا از هم الگوریتمی بنویسیم. برای کشف کوچکترین عدد در بین سه عدد مجزا باید هم از عملگرهای مقایسه‌ای استفاده کنیم و هم از عبارت‌های شرطی.

تمام مراحل الگوریتم مورد استفاده برای این مسئله را یک به یک در پایین، توضیح داده‌ایم.

1. ابتدا سه عدد مجزا را در ورودی دریافت کرده و در متغیرهای number1  و number2  و number3  جای‌گذاری می‌کنیم.
2. سپس به ترتیب متغیرها را با یکدیگر برای پیدا کردن کوچکترین عدد مقایسه می‌کنیم. یعنی اول متغیرهای number1  و number2  را با هم مقایسه کرده و عدد کوچک‌تر را پیدا می‌کنیم.
3. سپس عدد کوچکتر از حاصل مقایسه قبلی را با عدد number3  مقایسه می‌کنیم.
4. در نهایت کوچکترین عدد کشف شده را به خروجی ارسال می‌کنیم.

۱۰. محاسبه مجموعه اعداد از ۱ تا N

در این مسئله باید الگوریتمی بنویسیم که مجموعه اعداد از ۱ تا N را محاسبه کند. برای محاسبه مجموعه اعداد از ۱ تا N لازم است که ابتدا مقدار انتهای این محدوده را در ورودی دریافت کنیم. سپس از حلقه و دستور‌های تکراری برای محاسبه جواب استفاده می‌کنیم.

تمام مراحل الگوریتم مورد استفاده برای این مسئله را یک به یک در پایین، توضیح داده‌ایم.

1. در ابتدا حد بالای این محدوده عددی را از ورودی دریافت کرده و در متغیر n  قرار می‌دهیم.
2. سپس برای نگهداری حاصل جمع اعداد با هم متغیری را تعریف کرده و برابر با 0  قرار می‌دهیم. کد: sum = 0
3. شمارنده‌ای را برابر با 1  قرار می‌دهیم. کد: i=1
4. وارد حلقه می‌شویم و مقدار شمارنده حلقه را به علاوه sum  می‌کنیم. کد: i + sum
5. مقدار i  را یک واحد افزایش می‌دهیم.
6. تا زمانی که شرط i == n برقرار نشده مراحل ۴ و ۵ را تکرار می‌کنیم.
7. وقتی شرط i == n برقرار شد، کار حلقه به پایان رسیده و جواب مسئله محاسبه شده است. مقدار sum  را به عنوان جواب به خروجی ارسال می‌کنیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

با فرض اینکه در ورودی کد بالا، عدد 10  را وارد کنیم، خروجی زیر در کنسول پایتون نمایش داده می‌شود.

Enter a number (n): 
10
The sum of numbers from 1 to 10 is: 55

توجه: می‌توان مسئله بالا را برای محدوده عددی خاصی به غیر از ۱ تا N نیز محاسبه کرد، یعنی از M تا N. فقط باید مقدار M را هم در ورودی دریافت کنیم. سپس در ابتدای کار حلقه، مقدار i  را برابر با M قرار دهیم.

۱۱. بررسی مثبت یا منفی یا صفر بودن عدد داده شده

در این مسئله باید الگوریتمی بنویسیم که مثبت، منفی یا صفر بودن عدد داده شده را بررسی کند. می‌دانیم که اعداد مثبت بزرگ‌تر از صفر و اعداد منفی کوچک‌تر از صفر هستند. برای حل این مسئله از ساختار شرطی و عملگر مقایسه‌ای استفاده می‌کنیم.

در پایین الگوریتم ساده با جواب را برای این مسئله به صورت مرحله‌به‌مرحله نوشته‌ایم.

1. در این مسئله هم مانند بقیه موارد، ابتدا عدد مورد نظر را از طریق ورودی دریافت کرده و در متغیری با نام دلخواه number  قرار می‌دهیم.
2. سپس از دو شرط مختلف استفاده می‌کنیم. ابتدا بررسی می‌کنیم که اگر عبارت number > 0  صحیح بود، پس عدد مثبت است و کلمه Positive  را در خروجی برمی‌گردانیم.
3. اگر عبارت مقایسه‌ای number == 0  برقرار بود، پس عدد صفر است. در خروجی عبارت Zero  را برمی‌گردانیم.
4. اگر هیچ‌کدام از شرط‌های بالا برقرار نبود، پس عدد منفی است. در خروجی عبارت Negative  را برمی‌گردانیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

توجه: در برنامه نویسی کامپیوتر، داخل بلوک‌های شرطی که چند شرط به صورت سلسله وار پشت هم قرار گرفته‌اند، هر شرطی که برقرار باشد، مانع از بررسی عبارت‌های شرطی بعد از خود می‌شود و فقط دستور‌های داخل آن بلوک شرطی خاص، اجرا می‌شوند.

۱۲. معکوس کردن کلمه داده شده

در این مسئله، برای این‌که الگوریتم ساده با جواب را برای معکوس کردن کلمه داده شده نشان دهیم، باید دقت بیشتری در نوشتن الگوریتم داشته باشیم. برای معکوس کردن کلمه داده شده، لازم است که کاراکترهای آن رشته از انتها به ابتدا پیمایش شوند.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

تمام مراحل الگوریتم مورد استفاده برای این مسئله را یک به یک در پایین، توضیح داده‌ایم.

1. ابتدا در ورودی کلمه‌ای را دریافت می‌کنیم و در متغیری با نام دلخواه word  قرار می‌دهیم.
2. کل رشته داده شده را به صورت کاراکتر به کاراکتر در ساختار داده‌ای مانند لیست در پایتون ذخیره می‌کنیم.
3. سپس رشته خالی با نام دلخواه reversed_word  ایجاد می‌کنیم.
4. با کمک ساختار حلقه، رشته اصلی را از انتها - بیشترین اندیس رشته - تا به ابتدا - اندیس شماره 0  - پیمایش می‌کنیم.
5. در هر بار چرخش حلقه، کاراکتر مشاهده شده را به رشته خالی reversed_word  اضافه می‌کنیم.
6. مراحل ۴ و ۵ را تا زمانی تکرار می‌کنیم که تمام کاراکترهای رشته اصلی پیمایش شده و به رشته reversed_word  اضافه شوند.
7. محتوای رشته reversed_word پاسخ این مسئله است. آن را به خروجی ارسال می‌کنیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

برای حل مسئله بالا در زبان پایتون فقط کافی است که رشته اصلی را از ورودی دریافت کرده و در متغیری ذخیره کنیم. متغیر مورد نظر به صورت خود کار به لیستی از کاراکتر‌های تشکیل دهنده کلمه ورودی تبدیل می‌شود و قابل پیمایش است.

در پایین روش ساده‌تر دیگری را برای حل مسئله بالا نمایش داده‌ایم.

با فرض اینکه در ورودی کد بالا، کلمه Faradars   را وارد کنیم، خروجی زیر در کنسول پایتون نمایش داده می‌شود.

Enter a word: 
Faradars
The reversed word is: sradaraF

برای حل این مسئله از انواع متدهای رشته در پایتون نیز می‌توان استفاده کرد.

‍۱۳. بررسی بخش پذیر بودن یک عدد به عدد دیگر

در این مسئله باید الگوریتمی بنویسیم که بخش‌پذیر بودن عدد داده شده به عدد دیگری را محاسبه کند. برای محاسبه بخش‌پذیری از تقسیم باقیمانده - این تقسیم یکی از انواع عملگرهای ریاضی در برنامه نویسی است. - در کنار ساختار شرطی و عملگر مقایسه‌ای برابری استفاده کنیم.

تمام مراحل الگوریتم مورد استفاده برای این مسئله را یک به یک در پایین، توضیح داده‌ایم.

1. ابتدا دو عدد مجزا از هم را در ورودی دریافت کرده و در متغیرهای number1  و number2  قرار می‌دهیم.
2. فرض کنیم که می‌خواهیم بخش‌پذیری عدد number1  را بر عدد درون متغیر number2  محاسبه کنیم.
3. بنابراین، باید با استفاده از عملگر %  حاصل تقسیم باقیمانده صحیح بین این دو عدد را به شکل number1 % number2  محاسبه می‌کنیم. نتیجه این محاسبه را به متغیر remainder  اختصاص می‌دهیم.
4. صفر بودن مقدار remainder  را با استفاده از عملگر مقایسه‌ای ==  و به شکل remainder == 0  بررسی می‌کنیم.
5. اگر این عبارت مقایسه‌ای برقرار بود. یعنی عدد number1 بر عدد درون متغیر number2  بخش‌پذیر است. پس در خروجی کلمه Divisible  را نمایش می‌دهیم.
6. اگر این عبارت مقایسه‌ای برقرار نبود. یعنی عدد number1 بر عدد درون متغیر number2  بخش‌پذیر نیست. پس در خروجی عبارت Not Divisible  را نمایش می‌دهیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

با فرض اینکه در ورودی کد بالا، به ترتیب عددهای 10  و 2 را وارد کنیم، خروجی زیر در کنسول پایتون نمایش داده می‌شود.

Enter the first number: 
10
Enter the second number: 
2
Divisible

با فرض اینکه در ورودی کد بالا، به ترتیب عددهای 10  و 3 را وارد کنیم، خروجی زیر در کنسول پایتون نمایش داده می‌شود.

Enter the first number: 
10
Enter the second number: 
3
Not Divisible

توجه: اگر در ابتدا عدد دوم - یعنی مقدار متغیر number2  برابر با 0  قرار داده شد. قبل از انجام هر محاسبه و عملیاتی باید پیغام خطا نمایش دهیم. زیرا هیچ عددی بر صفر تقسیم نمی‌شود.

۱۴. الگوریتم محاسبه مقدار میانگین سه عدد

در این مسئله خواسته شده که مقدار میانگین سه عدد مجزا را محاسبه کنیم. برای محاسبه میانگین سه عدد از عملگرهای ساده ریاضی استفاده می‌کنیم.

در پایین الگوریتم ساده با جواب مورد استفاده برای حل این مسئله را قدم‌به‌قدم نوشته‌ایم.

1. در ورودی، سه عدد مجزا از هم را گرفته و به ترتیب در متغیر‌هایی با نام‌های number1  و number2  و number3  ذخیره می‌کنیم.
2. هر سه عدد را با استفاده از کد sum = number1 + number2 + number3  با هم جمع کرده و حاصل جمع را به متغیر sum  تخصیص می‌دهیم.
3. مقدار متغیر sum  را تقسیم بر 3  کرده و در متغیر result  ذخیره می‌کنیم.
4. نتیجه تقسیم برابر با جواب است. بنابراین مقدار متغیر result  را به عنوان نتیجه به خروجی ارسال می‌کنیم.

در بخش پایین کدهای مربوط به الگوریتم بالا را با زبان پایتون پیاده‌سازی کرده‌ایم.

با فرض اینکه در ورودی کد بالا، عددهای 10   و 2   و 21 را وارد کنیم، خروجی زیر در کنسول پایتون نمایش داده می‌شود.

Enter the first number: 
10
Enter the second number: 
2
Enter the third number: 
21
The average of the three numbers is: 11.0

آموزش پایتون به نوجوانان در فرادرس

زبان برنامه نویسی پایتون، بخاطر قدرت و سادگی در آموزش به یکی از محبوب‌ترین و رایج‌ترین زبان‌های برنامه‌نویسی برای افراد مبتدی تبدیل شده است. در صورتی که بخواهید الگوریتم ساده با جواب هر مسئله مطرح شده در این مطلب را برنامه‌ نویسی کنید، استفاده از پایتون یکی از آسان‌ترین روش‌ها است. وب‌سایت فرادرس با تولید مطالب و فیلم‌های آموزشی مختلف به یکی از بزرگترین و قوی‌ترین تولیدکنندگان محتوای آموزشی فارسی تبدیل شده است. زبان پایتون نیز یکی از جذاب‌ترین دوره‌ها در میان محتواهای آموزشی ویدیویی و متنی برای نوجوانان است. یکی از گزینه‌‌های مناسب برای شروع یادگیری این زبان برنامه‌نویسی، مجموعه آموزش پایتون برای نوجوانان است. فیلم‌های معرفی شده در زیر، از این مجموعه آموزشی معرفی شده‌اند.

• فیلم آموزش برنامه نویسی پایتون ویژه نوجوانان، بخش یکم در فرادرس
• فیلم آموزش طراحی رابط کاربری گرافیکی GUI با کتابخانه Tkinter در پایتون با فرادرس
• فیلم آموزش برنامه نویسی پایتون همراه با مثال های عملی در فرادرس
• فیلم آموزش رابط گرافیکی پای کیوت PyQt در پایتون از فرادرس

برای دیدن فیلم‌های بیشتر می‌توانید بر روی تصویر بالا کلیک کرده یا از فیلم‌های موجود در مجموعه آموزش برنامه نویسی پایتون Python از مقدماتی تا پیشرفته دیدن کنید.

۱۵. محاسبه تعداد روز‌ها در چند هفته مشخص

در این مسئله برای محاسبه تعداد روز‌ها در تعداد هفته مشخص شده، باید الگوریتم ساده‌ای بنویسیم. می‌دانیم که هر هفته دارای ۷ روز است. پس تنها داده مورد نیاز تعداد هفته‌هاست.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

در پایین، الگوریتم ساده با جواب مورد استفاده برای این مسئله را مرحله‌به‌مرحله نوشته‌ایم.

1. در ورودی عددی را با عنوان تعداد هفته‌ها دریافت کرده و در متغیری با نام دلخواه weeks  ذخیره می‌کنیم.
2. برای محاسبه روز‌ها، تعداد هفته‌ها را ضرب در ۷ می‌کنیم. در این مرحله از عبارت ریاضی weeks * 7  استفاده می‌کنیم.
3. حاصل ضرب بدست آمده همان جواب مسئله است. جواب را به خروجی ارسال می‌کنیم.

جمع‌بندی

در این مطلب از مجله فرادرس به بررسی ۱۵ مورد الگوریتم ساده با جواب مربوط به آن‌ها پرداخته‌ایم. ابتدا توضیح مختصری را درباره روش نوشتن الگوریتم بیان کرده‌ و سپس الگوریتم ساده با جواب مربوط به همه ۱۵ مسئله مطرح شده را یک به یک ارائه کردیم.

تمام مسائل مطرح شده از بین مسائل ساده‌ای انتخاب شده‌اند که در دوره‌های ابتدایی ریاضیات و برنامه نویسی به دانش‌آموزان عرضه می‌شوند. در هر مورد به صورت جداگانه ابتدا مسئله را مطرح کرده‌ایم. سپس راه حل مسئله را به زبان قابل درک برای انسان بیان کرده و از روی آن شبه کد مربوط به الگوریتم حل سوال پیاده‌سازی شده‌ است.