الگوریتم جنگل ایزوله — راهنمای کاربردی

پیدا کردن نقاط پرت (Outlier)، کاری است که باید تقریبا در هر گونه تحلیل‌های آماری صورت گیرد. وجود نقاط نامتعارف یا ناهنجار، باعث ایجاد خطا در مدل‌های آماری شده و پیش‌بینی را با مشکل مواجه می‌کند. به همین دلیل شناسایی ناهنجاری‌ها (Anomaly Detection) در علم داده (Data Science) از اهمیت زیادی برخوردار است. در این راستا مطلبی که در ادامه آمده است را به یکی از روش‌های آماری به نام الگوریتم جنگل ایزوله (Isolation Forest Algorithm) اختصاص داده‌ایم تا با استفاده از آن، کاربران بتوانند نقاط ناهنجار را شناسایی و از تحلیل خود خارج کنند.

برای آشنایی با نقاط ناهنجار و شیوه‌های دیگر شناسایی آن‌ها بهتر است نوشتارهای دیگر مجله فرادرس به عنوان تشخیص ناهنجاری (Anomaly Detection) — به زبان ساده و مشاهده ناهنجار و شناسایی آن در SPSS — راهنمای کاربردی را مطالعه کنید. همچنین خواندن نوشتارهای رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی و نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده نیز خالی از لطف نیست.

الگوریتم جنگل ایزوله

الگوریتم جنگل ایزوله (Isolation Forest) یا جنگل جداسازی، یک الگوریتم «یادگیری بدون نظارت» (Unsupervised Learning Algorithm) برای تشخیص ناهنجاری (Anomaly) است که برای جداسازی نقاط پرت (Outlier) به کار می‌رود. البته در اغلب روش‌های شناسایی نقاط پرت، بقیه نقاط که رفتار عادی دارند مورد ارزیابی قرار گرفته و براساس رفتار آن‌ها، نقاط پرت مشخص می‌شوند در حالیکه در الگوریتم جنگل ایزوله از ابتدا این گونه نقاط مورد بررسی قرار می‌گیرند.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

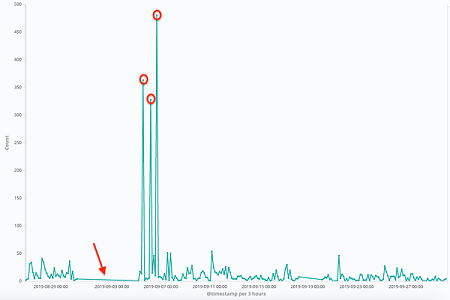
در آمار، یک ناهنجاری یا یک مشاهده نامتعارف، رویداد یا مقداری است که انحراف زیادی از سایر مقادیر داشته و به نظر رفتاری مغایر با بقیه نقاط ارائه می‌کند. به عنوان مثال، به نموداری که در تصویر 1 ظاهر شده توجه کنید. این نمودار نشان دهنده ترافیک ورودی به سرور وب یک سایت است که براساس تعداد درخواست‌ها در فواصل 3 ساعته، برای یک دوره یک ماه تنظیم شده است.

با نگاه کردن به این نمودار کاملاً مشهود است که برخی از نقاط (که با دایره قرمز رنگ مشخص شده‌اند) به طور غیرمعمولی بزرگ‌تر از دیگر مقادیر هستند. این طور به نظر می‌رسد که سرور وب در آن زمان مورد حمله (DDoS) قرار گرفته باشد. از طرف دیگر، قسمت مسطح این نمودار (که با فلش قرمز مشخص شده) نیز غیر عادی به نظر می‌رسد و احتمالاً نشانه اشکال در عملکرد سرور در این دوره زمانی است.

ناهنجاری های موجود در یک مجموعه داده بزرگ ممکن است دارای الگوهای بسیار پیچیده‌ای باشد که تشخیص اکثر آن نقاط در اغلب موارد دشوار است. به همین دلیل تشخیص ناهنجاری برای استفاده از تکنیک‌های یادگیری ماشین مناسب است و نمی‌توان به تنهایی با نگاه کردن به نمودار، نقاط ناهنجار را شناسایی کرد.

متداول‌ترین روش‌هایی که برای تشخیص ناهنجاری استفاده می‌شود مبتنی بر ساختن الگو یا نمایه‌ای (Profile) از نقاط هنجار یا «طبیعی» (Normal) است. به این ترتیب نقاط ناهنجاری به عنوان مواردی در مجموعه داده‌ها شناخته می‌شوند که با نقاط هنجار تفاوت زیادی دارند.

اما الگوریتم جنگل ایزوله از یک رویکرد متفاوت استفاده می‌کند به این معنی که به جای تلاش برای ساختن یک مدل از موارد و مشاهدات هنجار، مستقیما نقاط غیرعادی و ناهنجار را در مجموعه داده جدا می‌کند. مهمترین مزیت این روش امکان بهره‌برداری از تکنیک‌های نمونه‌گیری است بطوری که برای روش‌های مبتنی بر الگوهای نرمال این کار امکان‌پذیر نبوده و در نتیجه الگوریتم جنگل ایزوله بسیار سریع با حافظه کم قادر به اجرای عملیات شناسایی است.

تاریخچه الگوریتم جنگل ایزوله

الگوریتم جنگل ایزوله (Isolation Forest) یا به اختصار IForest ابتدا توسط «فی فی تونی لیو» (Fei Tony Liu)، «کای مینگ تینگ» (Kai Ming Ting) و «ژوی هوآ ژو» (Zhi-Hua Zhou) در سال 2008 ارائه شد. آنان از دو ویژگی عددی داده‌های نامتعارف یا ناهنجار استفاده کردند:

• کم بودن تعداد این نقاط
• تفاوت زیاد مقادیر آن‌ها نسبت به مشاهدات هنجار

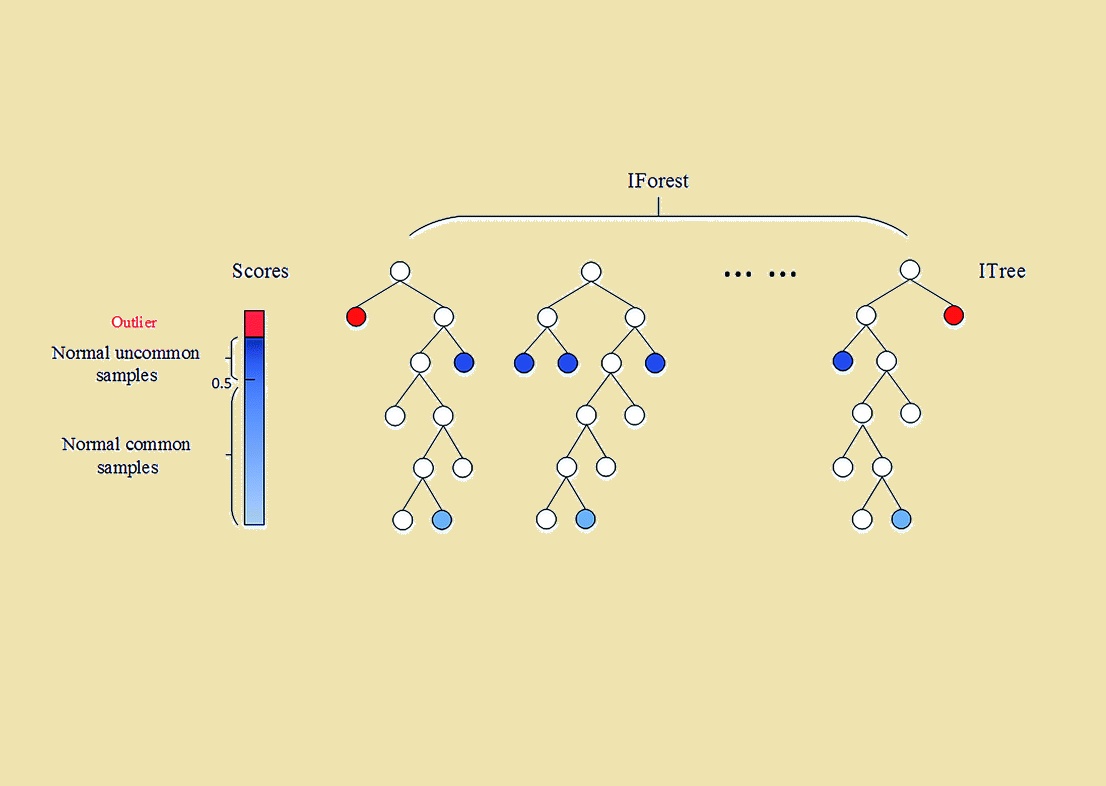
از آنجا که ناهنجاری‌ها کم و متفاوت هستند، در مقایسه با نقاط عادی جداسازی آن‌ها ساده‌تر است. الگوریتم IForest مجموعه‌ای از «درختان جداسازی» (iTrees) را برای مجموعه داده ایجاد می‌کند و ناهنجاری‌ها نقاطی هستند که بطور متوسط ​​مسیر کوتاه‌تری نسبت به بقیه نقاط در iTrees دارند.

در مقاله بعدی، که توسط همان نویسندگان در سال 2012 منتشر شد، مجموعه‌ای از آزمایشات را معرفی کردند تا نشان دهند که iForest دارای ویژگی‌های زیر است:

• از پیچیدگی زمانی خطی کم و نیاز به حافظه محدود برخوردار است.
• در مجموعه داده‌های با ابعاد بزرگ نیز قابل استفاده است.
• می‌توان الگوریتم را با استفاده از ناهنجاری‌های شناخته شده آموزش داد.
• بدون وجود آموزش مجدد می‌توان نتایج تشخیص با سطوح مختلف دسته‌بندی را ارائه داد.

در سال 2013، دو محقق دیگر به نام‌های «ژینگو دینگ» (Zhiguo Ding ) و «مینوری فیی» (Minrui Fei) چارچوبی را بر اساس iForest پیشنهاد دادند تا مشکل تشخیص ناهنجاری‌ها در جریان داده‌ها (Streaming Data) برطرف شود. کاربرد بیشتر iForest در جریان داده‌ها، در مقالات توسط «تان» (Tan) و «سوتو» (Susto) توضیح داده شده است.

يكي از مشكلات اصلي كاربرد iForest در تشخيص ناهنجاري، مربوط به خود مدل نیست، بلكه در روش محاسبه «نمره ناهنجاری» (Anomaly Score) است. این مشکل توسط «سهند حریری»، «ماتیاس کاراسکو» (Matias Carrasco Kind) و «رابرت برنر» (Robert J. Brunner) در مقاله‌ای که در سال 2018 منتشر کردند، مطرح گردید. آنان یک مدل بهبود یافته از iForest ارائه داnند که به نام «جنگل ایزوله توسعه یافته» (Extended Isolation Forest) یا به اختصار EIF شهرت دارد. در همان مقاله، نویسندگان پیشرفت‌های انجام شده در مدل اصلی و چگونگی توانایی ارتقاء و قابلیت اطمینان نمره ناهنجاری تولید شده برای یک نقطه را شرح دادند. این الگوریتم و نحوه پیاده‌سازی آن در نوشتارهای دیگر فرادرس مورد بحث قرار خواهد گرفت.

گام‌های الگوریتم جنگل ایزوله

براساس الگوریتم جنگل ایزوله، تشخیص موارد غیر عادی و ناهنجار در مجموعه داده انجام شده که البته آسان‌تر از پیدا یا جداسازی داده‌ها یا نقاط نرمال یا هنجار است. به منظور جداسازی یک نقطه، الگوریتم به صورت بازگشتی با انتخاب تصادفی یک ویژگی، تقسیم‌‌بندی‌هایی را روی نمونه داده‌ها ایجاد می‌کند و سپس بطور تصادفی یک مقدار آستانه برای جداسازی یا تفکیک مقادیر به صورت هنجار یا ناهنجار، بین حداقل و حداکثر مقادیر مجاز برای آن صفت یا ویژگی، تعیین می‌کند.

فیلم آموزش یادگیری ماشین با پایتون – ماشین لرنینگ با Python در فرادرس

کلیک کنید

نمونه‌ای از تقسیم‌بندی تصادفی در یک مجموعه داده دو بُعدی از نقاط تولید شده از توزیع نرمال دو متغیره را در دو وضعیت مختلف در تصویر ۲ و ۳ مشاهده می‌کنید. در تصویر ۲، نقطه هنجار مشخص شده و در تصویر ۳، مشاهده‌ای که نسبت به بقیه ناهنجار به نظر رسیده، جدا شده است.

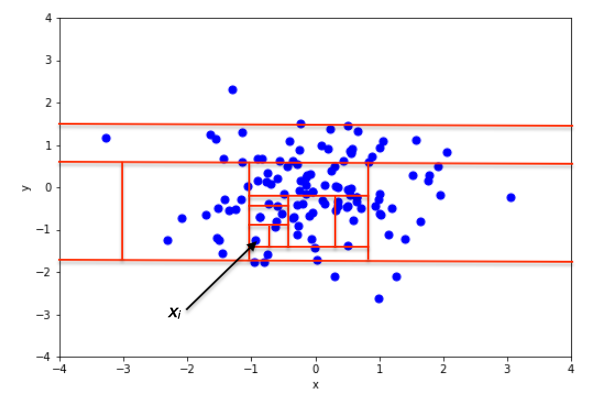
در این تصاویر بخش‌های لازم برای تشخیص نقاط بوسیله مربع‌های قرمز رنگ، دیده می‌شود. واضح است که تعداد بخش‌ها، برای جداسازی نقاط عادی و هنجار بسیار بیشتر از نقاط ناهنجار و نامتعارف است.

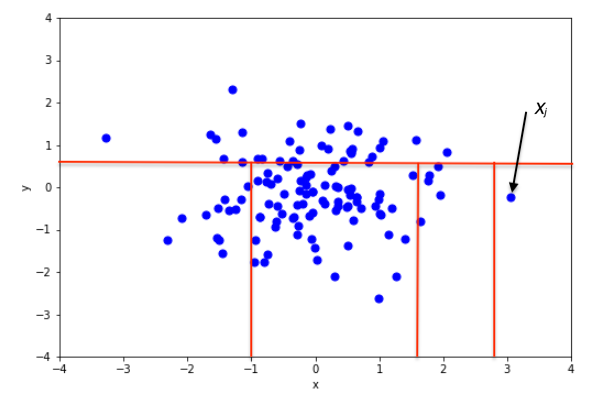
از دیدگاه ریاضیات، «بخش‌بندی بازگشتی» (Recursive Partitioning) می‌تواند توسط یک ساختار درختی (Tree Structure) به نام «درخت ایزوله» (Isolation Tree) یا iTree نشان داده شود، در حالی که تعداد بخش‌های مورد نیاز برای جداسازی یک نقطه را می‌توان به عنوان طول مسیر، درون یک ساختار درختی تعبیر کرد تا به یک گره پایانی (Terminating Node) برسیم. واضح است از ریشه درخت شروع به حرکت کرده‌ایم و مسیر از آنجا آغاز شده است. به عنوان مثال، طول مسیر $$x_i$$ در شکل 2 از طول مسیر $$x_j$$ در شکل 3 بیشتر است.

به منظور ساخت iTree، الگوریتم به صورت بازگشتی با انتخاب تصادفی یک ویژگی به نام q و مقدار آستانه به نام p به طور تصادفی بخش‌بندی را انجام می‌دهد و تا زمانی که گره شامل فقط یک نقطه باشد یا تمام داده‌های گره دارای مقادیر یکسان باشند، ادامه پیدا می‌کند.

وقتی iTree کاملاً رشد کرد، هر نقطه از X در یکی از گره‌های خارجی جدا می‌شود. به طور شهودی، نقاط غیر عادی و ناهنجار مواردی هستند که دارای طول مسیر کوچکتری در درخت هستند. توجه داشته باشید که که طول مسیر $$h (x_i)$$ از نقطه $${\ displaystyle x_ {i} \in X }$$ به عنوان تعداد اضلاعی است که $$x_i$$ از گره ریشه فاصله دارد.

ویژگی‌های الگوریتم جنگل ایزوله

در ادامه به بعضی از ویژگی‌هایی مهم در جنگل ایزوله به صورت فهرست‌وار خواهیم پرداخت.

زیر نمونه‌گیری (Sub-sampling): از آنجایی که iForest نیازی به جداسازی همه نقاط متعارف عادی ندارد، می‌تواند بیشتر نقاط نمونه آموزشی (Training Set) را نادیده بگیرد. در نتیجه، iForest هنگامی که اندازه نمونه، کوچک باشد، بسیار خوب کار می‌کند. این ویژگی در بین الگوریتم‌های دیگر کمتر دیده می‌شود.

فیلم آموزش نمونه گیری در نرم افزار آر R در فرادرس

کلیک کنید

غرق شدن: وقتی نمونه‌های متعارف و هنجار خیلی نزدیک به ناهنجاری‌ها هستند، تعداد بخش‌بندی‌های مورد نیاز برای جدا کردن ناهنجاری‌ها افزایش می‌یابد که این حالت را به نام پدیده‌ای به نام «غرق‌شدن» (Swamping) می‌شناسند. این امر باعث می‌شود که iForest تفاوت بین ناهنجاری‌ها و نقاط عادی را به کندی و با تکرارهای زیاد تشخیص داده یا به طور کامل دچار واگرایی در پاسخ‌ها شود. به این معنی که با هر بار تکرار الگوریتم، نقاط متفاوتی را به عنوان ناهنجاری شناسایی می‌شوند.

پنهان ماندن: هنگامی که تعداد ناهنجاری‌ها زیاد باشد، ممکن است که برخی از این نقاط در یک خوشه متراکم و بزرگ قرار بگیرند و جدا کردن ناهنجاری‌های را توسط الگوریتم درخت ایزوله دشوارتر کند. درست مانند مشکل غرق شدن، مشکل پنهان ماندن (Masking) نیز  در زمانی که تعداد نقاط در نمونه زیاد باشد، رخ می‌دهد.

داده‌های چند بعدی با ابعاد بالا: یکی از اصلی‌ترین محدودیت‌های روش‌های مبتنی بر روش‌های استاندارد که برمبنای محاسبه تابع فاصله (Distance Function) کار می‌کنند، ناکارآمدی آنها در برخورد با مجموعه‌های داده با ابعاد زیاد است. دلیل اصلی این امر آن است که در یک فضای ابعاد بالا، نقاط تقریبا دارای فاصله یکسانی نسبت به یکدیگر هستند، بنابراین استفاده از یک اندازه‌گیری مبتنی بر فاصله بسیار ناکارآمد عمل می‌کند. متأسفانه، داده‌های با ابعاد بالا بر عملکرد تشخیص iForest نیز تأثیر می‌گذارند، اما می‌توان با افزودن یک آزمون به منظور انتخاب ویژگی‌های خاص و موثر، عملکرد را به شکلی تغییر داد تا ابعاد فضای نمونه کاهش یابد.
مشاهدات هنجار و متعارف: الگوریتم جنگل ایزوله (iForest) حتی اگر مجموعه آموزشی دارای فقط نقاط متعارف باشند نیز به خوبی عمل می‌کند. دلیل این امر آن است که iForest توزیع داده‌ها را به گونه‌ای توصیف می‌کند که مقادیر بزرگ برای طول مسیر $$h (x_i)$$ ملاک عمل است، در نتیجه وجود ناهنجاری‌ها نسبت به عملکرد تشخیص iForest بی‌ارتباط است.

گام‌های اصلی الگوریتم جنگل ایزوله

تشخیص ناهنجاری با الگوریتم «جنگل ایزوله» (Isolation Forest) فرآیندی است که از دو مرحله اصلی تشکیل شده است:

• در مرحله یا گام اول، از مجموعه داده‌های آموزشی (Training Set) برای ساخت iTrees استفاده می‌شود، این کار بوسیله عملیاتی که در قبل اشاره شد، صورت می‌گیرد.
• در مرحله یا گام دوم، هر نمونه از مجموعه آزمایشی (Testing Set) از طریق ساخت iTrees از مرحله قبل منتقل می‌شود و یک «نمره ناهنجاری» مناسب با استفاده از الگوریتم به آن اختصاص می‌یابد.

هنگامی که به تمام موارد موجود در مجموعه آزمایشی، نمره ناهنجاری اختصاص داده شد، می‌توان هر نقطه‌ای را که نمره آن بیشتر از یک آستانه از پیش تعریف شده باشد را به عنوان «ناهنجاری» در نظر بگیریم.

نمره ناهنجاری

الگوریتم محاسبه نمره ناهنجاری یک نقطه، مبتنی بر دیگر مشاهدات است بطوری که ساختار iTrees آن معادل با ساختار درختی جستجو دودویی (BST) است. به این معنی که رسیدن به یک گره خارجی از iTree معادل با یک جستجوی ناموفق در BST است. در نتیجه، برآورد میانگین طول مسیر $$h (x)$$ برای رسیدن به گره‌های خارجی به صورت زیر محاسبه می‌شود.

$$\large {\displaystyle c(m)={\begin{cases}2H(m-1)-{\frac {2(m-1)}{n}}&{\text{for }}m>2\\1&{\text{for }}m=2\\0&{\text{otherwise}}\end{cases}}}$$

بطوری که $$n$$ تعداد داده‌های آزمایشی و $$m$$ حجم نمونه و $$H$$، «عدد هارمونیک» (Harmonic Number) است که بوسیله رابطه $$H(i) = \ln(i) +\gamma$$ محاسبه می‌شود. توجه دارید که $$\gamma$$ همان «ثابت اویلر-ماسکرونی» (Euler-Mascheroni constant) است.

مقدار $$c (m)$$ در بالا نشانگر میانگین $$h (x)$$ است که برحسب $$m$$ مشاهده نوشته شده، بنابراین می‌توانیم از آن برای نرمال سازی $$h (x)$$ استفاده کنیم و تخمین نمره ناهنجاری را برای نمونه معین بدست آوریم.

$$\large {\displaystyle s(x,m)=2^{\frac {-E(h(x))}{c(m)}}}$$

در رابطه بالا، $$E(h(X))$$ امید ریاضی یا مقدار مورد انتظار مقادیر مختلف $$h(x)$$ روی مجموعه درختان iTrees است. در این مورد به نکات زیر توجه کنید.

• اگر $$s$$ به ۱ نزدیک باشد، می‌توان نتیجه گرفت که $$x$$ با احتمال زیاد یک نقطه ناهنجار تلقی می‌شود.
• نزدیکی $$s$$ به $$0.5$$ بیانگر هنجار یا متعارف بودن نقطه است.
• اگر برای همه مقادیر یک نمونه تصادفی، امتیاز یا مقدار $$s$$ به $$0.5$$ نزدیک باشد، باید انتظار داشت که همه نقاط هنجار بوده و مجموعه داده شامل ناهنجاری نیست.

نحوه اجرای و پیاده‌سازی الگوریتم جنگل ایزوله توسط پایتون در نوشتار دیگری از مجله فرادرس مورد بررسی قرار خواهد گرفت.

خلاصه و جمع‌بندی

در این نوشتار با الگوریتم جنگل ایزوله به عنوان روشی برای شناسایی ناهنجاری و نقاط پرت در داده‌ها، آشنا شده، خصوصیات و ویژگی‌های منحصر به فرد این الگوریتم (IForest) را یادآوری کردیم. هر چند شیوه‌های مختلفی برای شناسایی ناهنجاری وجود دارد ولی نمی‌توان دقیق‌ترین آن‌ها را بدون توجه به رفتار داده‌ها مشخص کرد. در نتیجه ترسیم نمودارها و شناخت از نحوه تغییرات داده‌ها نقش مهمی در تعیین مشاهدات ناهنجار یا دورافتاده دارد.