آزمون ویلکاکسون رتبه علامت دار — اجرا در SPSS

۵۶۴۷ بازدید

آخرین به‌روزرسانی: ۰۸ خرداد ۱۴۰۲

زمان مطالعه: ۹ دقیقه

آزمون ویلکاکسون رتبه علامت دار — اجرا در SPSS

بیشتر روش‌های آمار ناپارامتری برپایه رتبه‌ها و توزیع‌ آن‌ها است. توسعه آمار ناپارامتری و روش‌های آن توسط «فرانک ویلکاکسون» (Frank Wilcoxon) شیمی‌دان و آمارشناس آمریکای در سال ۱۹۴۵ طی مقاله‌ای که منتشر کرد رخ داد. این مقاله و مقاله‌ای که «هنری مَن» (Henry Mann) و «دونالد ویتنی» (Donald Ransom Whitney) در سال 1۹4۷ منتشر کردند، باعث شد که توجه به آمار ناپارامتری و انجام تحلیل بر روی جوامع آماری که توزیع احتمالی آن‌ها نرمال یا گاوسی نیست، گسترش پیدا کند. از جمله این روش‌های می‌توان به تحلیل‌های ناپارامتری، «آزمون ویلکاکسون جمعی رتبه‌ای» (Wilcoxon Sum-Rank Test) و «آزمون ویلکاکسون رتبه علامت‌دار» (Wilcoxon Signed-Rank Test) اشاره کرد. آزمون ویلکاکسون جمعی رتبه‌ای درست به مانند «آزمون یو من ویتنی» (Mann-Whitney U Test) است که در دیگر نوشتار فرادرس با عنوان آزمون یو من ویتنی (Mann-Whitney U) در SPSS — راهنمای کاربردی معرفی و مورد بررسی قرار گرفته است.

فهرست مطالب این نوشته

آزمون ویلکاکسون رتبه علامت دار

خلاصه

Wilcoxon rank test — ویلکاکسون پایه‌گذار آمار ناپارامتری

در این نوشتار به بررسی «آزمون رتبه علامت‌دار» (Wilcoxon Signed-Rank Test) پرداخته و در محیط SPSS با نحوه اجرا و تفسیر خروجی‌ها آن آشنا می‌شویم. به منظور آشنایی بیشتر با مفاهیم به کار رفته در آمار ناپارامتری بهتر است نوشتار آمار پارامتری و ناپارامتری — انتخاب روش های تحلیل و آزمون علامت (Sign Test) — به زبان ساده را مطالعه کنید. همچنین خواندن مطلب آزمون یو من ویتنی (Mann-Whitney U) در SPSS — راهنمای کاربردی نیز خالی از لطف نیست.

آزمون ویلکاکسون رتبه علامت دار

آزمون ویلکاکسون رتبه علامت‌دار به منظور انجام بررسی دو نمونه وابسته یا انطباق بین دو نمونه به کار گرفته می‌شود. این آزمون را می‌توان مشابه آزمون t برای گروه‌های وابسته برای میانگین جامعه‌ غیرنرمال، در نظر گرفت.

فیلم آموزش نرم افزار MedCalc برای تجزیه و تحلیل و انجام محاسبات آماری در فرادرس

کلیک کنید

هر چند این آزمون، ناپارامتری بوده و به توزیع داده‌ها بستگی ندارد ولی برای انجام این آزمون باید فرضیات زیر مورد بررسی قرار گیرد.

داده‌ها باید به صورت زوجی و از یک جامعه گرفته شده باشند.
هر مولفه از زوج‌ها به صورت تصادفی انتخاب شده و مستقل از نمونه‌های دیگر باشند.
نوع یا مقیاس داده‌ها باید به صورت فاصله‌ای یا نسبتی باشند تا بتوان تفاوت بین مقدار آن‌ها را بدست آورد و این تفاضل‌ها را رتبه‌بندی کرد. به این ترتیب باید مطمئن شد که تفاضل مقدارهای زوج‌ها به صورت مقیاس ترتیبی باشند.

آماره و مراحل اجرای آزمون

فرض کنید که زوج‌های تصادفی با اندازه نمونه $$n$$‌ در اختیار داریم. بنابراین تعداد مقدارها با توجه به زوج بودن نمونه‌ها برابر با $$2n$$ خواهد بود. مشاهدات زوجی را نیز برحسب مولفه‌ها، به صورت $$x_{1,i}$$ و $$x_{2,i}$$ با توجه به $$i=1,2,\ldots,n$$‌ نشان می‌دهیم. در اینجا هدف از انجام آزمون فرض آماری، تعیین تفاوت در بین دو زوج‌ها است. به این ترتیب «فرض صفر» (Null Hypothesis) را یکسان بودن مقدارها در بین زوج‌ها در نظر گرفته و «فرض مقابل» (Alternative Hypothesis) را هم وجود اختلاف در بین زوج‌ها محسوب می‌کنیم. با توجه به این موضوعات، مراحل انجام آزمون مطابق با مقاله ویلکاکسون به صورت زیر خواهد بود.

برای همه مشاهات قدر مطلق اختلاف بین زوج‌ها $$ |x_{2,i}-x_{1,i}|$$ به ازاء $$i=1,2,\ldots,n$$‌ محاسبه و علامت (مثبت یا منفی بودن) این اختلاف $$\operatorname {sgn} (x_{2,i}-x_{1,i})$$ مشخص می‌شود. واضح است که منظور از $$\operatorname{sgn}$$ همان تابع علامت است به این معنی که اگر پارامتر تابع مثبت باشد، مقدار ۱ و در صورت منفی بودن پارامتر، مقدار ۱- را نشان می‌دهد. در صورتی که این اختلاف برابر با صفر باشد، مقدار تابع علامت نیز صفر خواهد بود.
زوج‌هایی که مقدار تابع علامت برایشان صفر است از تحلیل خارج می‌شوند. به این ترتیب $$n_r$$ را تعداد زوج‌های باقی‌مانده در نظر می‌گیریم. البته در مواقعی که اندازه نمونه خیلی کوچک باشد، برای آنکه تعداد مشاهدات کاهش نیابد می‌توان زوج‌هایی با این شرط را فقط در یکی از گروه‌های مقدار مثبت یا منفی ثبت کرد.
مقدار‌های حاصل از قدر مطلق اختلاف‌ها یعنی $$ |x_{2,i}-x_{1,i}|$$ را از کوچک به بزرگ مرتبه می‌کنیم.
رتبه‌های مربوط به قدرمطلق اختلاف‌ها را بدست می‌آوریم. واضح است که ممکن است رتبه‌های گره‌دار نیز برای بعضی از مقدارها بدست آید. در این حالت میانگین رتبه‌ها را برای چنین مشاهداتی در نظر می‌گیریم. به کوچکترین مقدار اختلاف، رتبه ۱ داده شده و رتبه اختلاف برای زوج $$i$$ام را با $$R_i$$ نشان می‌دهیم.
آماره $$W$$ را مطابق با رابطه زیر محاسبه می‌کنیم.

$$\large W=\sum _{{i=1}}^{{n_{r}}}[\operatorname{sgn}(x_{{2,i}}-x_{{1,i}})\cdot R_{i}]$$

آنچه که در گام پنجم محاسبه شد به مجموع رتبه‌های علامت‌دار معروف است. تحت فرض صفر، توزیع احتمالی $$W$$ پیچیده است ولی میانگین آن برابر با صفر و واریانس آن نیز برابر با رابطه زیر است.

$$\large \sigma^2_W ={\displaystyle {\frac {n_{r}(n_{r}+1)(2n_{r}+1)}{24}}}$$

خوشبختانه برای توزیع $$W$$ جدول‌هایی تهیه شده است که از طریق آن می‌توان ناحیه بحرانی را تشخیص داده و نسبت به رد یا تایید فرض صفر اقدام کرد. در مثالی که در ادامه مشاهده خواهید کرد، نحوه به کارگیری چنین جدول‌هایی مشخص شده است. به این صورت اگر $$W|< W_{\alpha, n_r}$$ باشد، فرض صفر رد خواهد شد.

نکته: اگر مقدار $$n_r$$ بزرگ باشد، می‌توان توزیع $$W$$ را نرمال با میانگین صفر و واریانس $$\sigma^2_W$$ در نظر گرفت. در این صورت قاعده تصمیم‌گیری را به شکل $$|z|<zـ{\alpha}$$ می‌نویسیم. واضح است که مقدار $$z$$ از رابطه زیر قابل محاسبه است.

$$\large z={\frac {W}{\sigma _{W}}},\;\; \sigma _{W}={\sqrt {\frac {n_{r}(n_{r}+1)(2n_{r}+1)}{24}}}$$

مثال

فرض کنید ۱۰ مشاهده زوجی با متغیرها $$x_{1,i}, x_{2,i}$$ با توجه به $$i=1,2\ldots,10$$ در اختیار داریم. با توجه به اینکه تعداد نمونه کمتر از حد انتظار برای اجرای آزمون t زوجی است، برای مقایسه یکسان بودن میانگین در بین زوج‌ها از آزمون ویلکاکسون رتبه‌های علامت‌دار استفاده می‌کنیم. محاسبات مطابق با جدول زیر انجام شده است.

$$x_{2,i}-x_{1,i}$$		$$x_{۱,i}$$	$$x_{2,i}$$	$$i$$
قدر مطلق	علامت	$$x_{۱,i}$$	$$x_{2,i}$$	$$i$$
15	1	110	125	1
7	1-	122	115	۲
5	1	125	130	۳
20	1	120	140	۴
0		140	140	۵
9	1-	124	115	۶
17	1	123	140	۷
12	1-	137	125	۸
5	1-	135	140	۹
10	1-	145	135	۱۰

حال اگر جدول را براساس رتبه‌ها مرتب کنیم، جدول زیر حاصل می‌شود. توجه داشته باشید که گره‌ها در رتبه‌ها بوسیله میانگین رتبه‌‌ها مشخص شده است.

$$x_{2,i}-x_{1,i}$$				$$x_{۱,i}$$	$$x_{2,i}$$	$$i$$
$$\operatorname{sgn}.R_i$$	$$R_i$$	قدر مطلق	علامت	$$x_{۱,i}$$	$$x_{2,i}$$	$$i$$
		0		140	140	5
1.5	1.5	5	1	125	130	3
1.5	1.5	5	1	135	140	9
3-	3	7	1-	122	115	2
4-	4	9	1-	124	115	6
5-	5	10	1-	145	135	10
6-	6	12	1-	137	125	8
7	7	15	1	110	125	1
8	8	17	1	123	140	7
9	9	20	1	120	140	4

به این ترتیب مجموع رتبه‌های علامت‌دار برای ۹ مشاهده (حذف مشاهده با مقدار اختلاف صفر) برابر با $$|1.5+1.5-3-4-5-6+7+8+9|=9$$ خواهد بود. به این ترتیب برطبق جدول زیر که مقدارهای بحرانی برای آماره ویلکاکسون را برحسب $$\alpha$$‌ مختلف نشان می‌دهد، فرض صفر رد نمی‌شود زیرا مقدار آماره آزمون برای داده‌ها بزرگتر از مقدار بحرانی است. در نتیجه یکسان بودن مولفه‌های اول و دوم رد نمی‌شود.

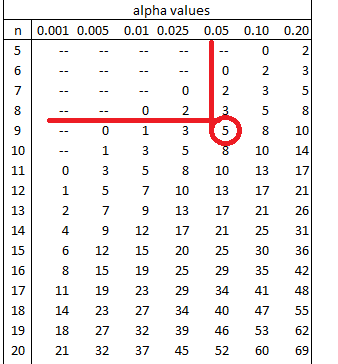
signed-ranks-table — جدول نقاط بحرانی آماره ویلکاکسون

اجرای آزمون ویلکاکسون رتبه علامت‌دار در SPSS

فرض کنید براساس مثال قبل، داده‌ها را در نرم‌افزار SPSS‌ وارد کرده‌ایم. باید توجه داشته باشید که برای ورود داده‌های زوجی از دو متغیر استفاده کرده و هر مشاهده که شامل دو مولفه است در یک سطر وارد کنید.

فیلم آموزش استنباط آماری پارامتری در Minitab (رایگان) در فرادرس

کلیک کنید

به این ترتیب می‌توان تصویر زیر را نتیجه ورود داده‌ها در جدول ویرایشگر داده‌های SPSS تصور کرد.

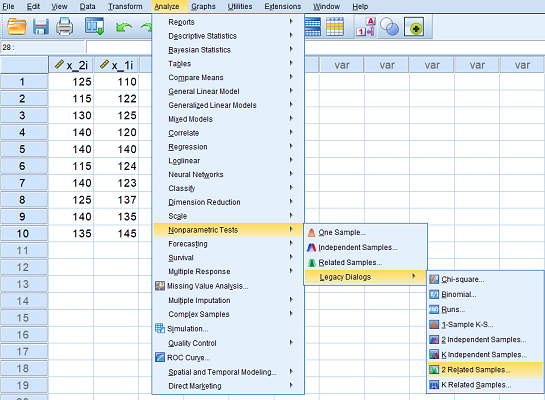
wilcoxon test in spss data

پس از ورود داده‌ها، مطابق با مسیری که در زیر اشاره شده است به پنجره اجرای فرمان مربوط به آزمون‌های ناپارامتری مقایسه دو نمونه وابسته دسترسی پیدا خواهید کرد.

Analyze ---> Nonparmeteric Tests ---> Legacy Dialog ---> 2 Related Samples

برای انجام آزمون کافی است متغیرهای مورد نظر را که در اینجا $$x_{2i}$$ و $$x_{1i}$$ هستند، به ترتیب در کادر Test Pairs قرار دهید. البته انتخاب گزینه Wilcoxon در کادر Test Type هم بیانگر استفاده از روش آزمون ویلکاکسون رتبه‌ علامت‌دار است. اگر می‌خواهید از توزیع دقیق آماره آزمون استفاده کنید با انتخاب دکمه Exact وارد پنجره Exact Tests خواهید شد.

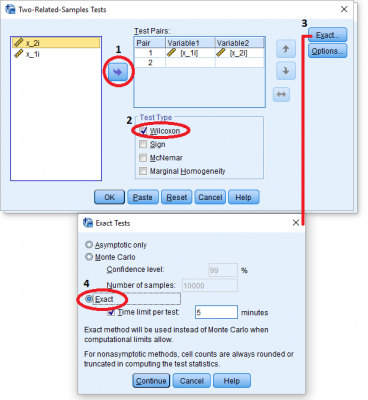
wilcoxon test in spss dialog

با انتخاب دکمه Continue به پنجره اصلی آزمون برگشته و می‌توانید با فشردن دکمه OK آزمون را اجرا کنید.

نکته: اگر اندازه نمونه بزرگ باشد ممکن است آزمون دقیق زمان زیادی بگیرد. به همین دلیل حداکثر زمان برای اجرای آزمون در کادر Time limit per test را ۵ دقیقه به عنوان پیش‌فرض در نظر گرفته‌اند. البته می‌توانید به دلخواه این زمان را تغییر دهید. اگر اندازه نمونه بزرگ باشد و بخواهید در زمان کوتاه‌تری نتایج را بدست آورید از گزینه Asymptotic only استفاده کنید، در این صورت توزیع مجانبی آماره برای انجام آزمون به کار خواهد رفت. همچنین برای تعیین واریانس برآورد نیز می‌توان از روش مونت‌کارلو استفاده کرد تا اگر اندازه نمونه کوچک است بتوان برآورد مناسب‌تر و با دقت بیشتری را بوسیله شبیه‌سازی مونت‌کارلو بدست آورد.

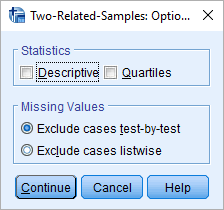
wilcoxon test in spss option

اگر در پنجره اصلی آزمون دکمه Options را انتخاب کنید، پنجره‌ای به مانند تصویر بالا مشاهده خواهید کرد. با انتخاب گزینه Descriptive، آمار توصیفی نظیر تعداد (N)، میانگین (Mean)، انحراف استاندارد (Standard Deviation)، حداقل (Minimum) و حداکثر (Maximum) متغیرها در پنجره خروجی ظاهر می‌شوند. گزینه Quantiles نیز باعث ظاهر شدن چارک‌ها خواهد شد. همچنین در قسمت Missing Values مشخص می‌کنید که اگر چند متغیر در آزمون به کار روند، با وجود یک یا چند مشاهده با مقدار گمشده، چه وضعیتی برای حذف آن‌ها رخ دهد. اگر گزینه Exclude cases test-by-test را انتخاب کنید، مشاهدات مربوط به هر متغیر آزمون که دارای مقدار گمشده هستند، حذف می‌شوند ولی اگر گزینه Exclude cases listwise را فعال کنید، آزمون برای مشاهداتی اجرا خواهد شد که در هیچ یک از متغیرها مقدار گمشده نداشته باشند.

نکته: اگر می‌خواهید از کد Syntax نرم‌افزار SPSS برای انجام این آزمون استفاده کنید باید دستورات زیر را در پنجره Syntax‌ وارد کرده و آن‌ها را اجرا کنید.

1DATASET ACTIVATE DataSet1.
2NPAR TESTS
3  /WILCOXON=x_1i WITH x_2i (PAIRED)
4  /MISSING ANALYSIS
5  /METHOD=EXACT TIMER(5).

به این ترتیب نتیجه اجرای آزمون ویلکاکسون رتبه علامت‌دار برای داده‌های زوجی مثال قبل به شکل زیر خواهد بود.

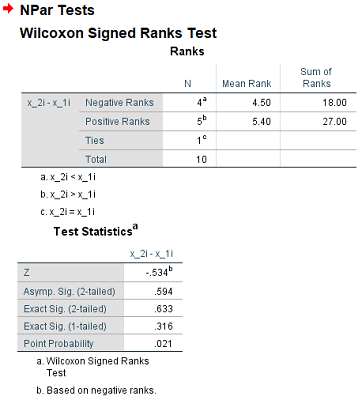
wilcoxon test in spss output

همانطور که مشاهده می‌کنید، در جدول Wilcoxon Signed Ranks test در ستون مجموع رتبه‌ها (Sum of Ranks)، مقدار «مجموع رتبه‌های منفی» (Negative Ranks) و «مجموع رتبه‌های مثبت» (Positive Ranks) ثبت شده است. بنابراین مجموع این رتبه‌ها با توجه به علامتشان برابر با ۹ خواهد بود. همچنین در جدول Test Statistics، آماره آزمون مجانبی (Z) محاسبه شده است. در عین حال مقدار احتمال (p-Value) برای آزمون مجانبی دو طرفه در سطر (Asymp. Sig (2-tailed و «یک طرفه» (One Tailed) و «دو طرفه» (Two Tailed) دقیق (.Exact Sig) ظاهر شده است.

فیلم آموزش تحلیل داده ها با نرم افزار مینی تب Minitab در فرادرس

کلیک کنید

بنابراین اگر منظور بررسی وضعیت یکسان بودن دو نمونه بوده، باید به نتیجه آزمون دو طرفه توجه کنیم. پس با توجه به رابطه زیر فرض صفر که یکسان بودن دو نمونه بوده، در سطح خطای آزمون 5٪ رد نمی‌شود. همانطور که دیده می‌شود، این همان نتیجه‌ای است که توسط جدول آزمون نیز بدست آوردیم.

$$\large Exact\; Sig.\;(2\; tailed)=.633 > 0.05$$

شیوه‌ای که در قسمت قبل برای اجرای آزمون ویلکاکسون رتبه علامت‌دار معرفی شد، روشی مرتبط با نسخه‌های قدیمی SPSS است. اگر می‌خواهید از امکانات نسخه‌های جدید‌تر SPSS استفاده کنید، مراحل اجرای دستور را مطابق با تصویر و با استفاده از مسیر زیر انجام دهید.

Analyze ---> Nonparametric Tests ---> Related Samples

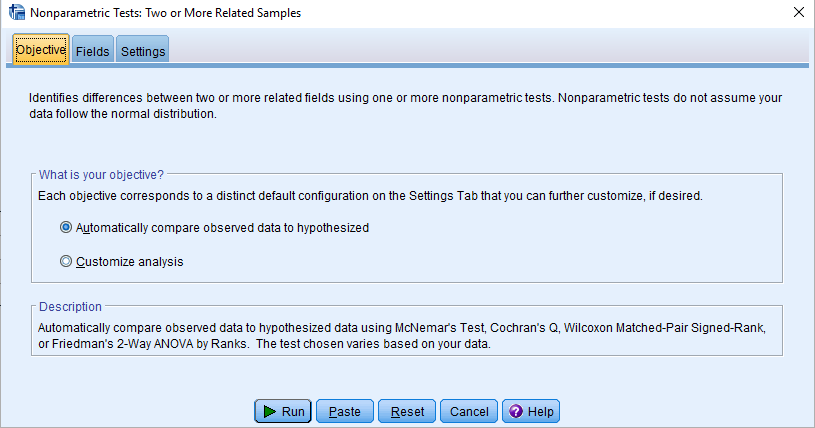
در پنجره ظاهر شده در برگه Objective می‌توانید هدف از انجام این گونه آزمون‌ها را مشخص کنید. البته در صورتی که گزینه ...Automatically را انتخاب کرده باشید، SPSS به طور خودکار متغیرها و نوع آزمون را تشخیص داده و با استفاده از دکمه Run، آزمون‌ها را اجرا می‌کند.

wilcoxon test in spss modern dialog

در برگه دوم یا Fields متغیرهایی که باید در آزمون به کار گرفته شوند، مشخص می‌شود. دقت داشته باشید که ترتیب ورود این متغیرها در تعیین تعداد رتبه‌های منفی و مثبت تاثیر گذار است.

wilcoxon test in spss modern dialog fields

در انتها نیز با انتخاب برگه Settings، نوع آزمون قابل انتخاب است. همانطور که در تصویر زیر مشاهده می‌کنید، آزمون ویلکاکسون رتبه علامت‌دار (Wilcoxon matched-pair Signed-Rank) انتخاب شده است.

wilcoxon test in spss modern dialog settings

نکته: برای آنکه این روش آزمون را در محیط Syntax به کار ببرید باید از کدهای زیر استفاده کنید.

1*Nonparametric Tests: Related Samples. 
2NPTESTS 
3  /RELATED TEST(x_2i x_1i) WILCOXON 
4  /MISSING SCOPE=ANALYSIS USERMISSING=EXCLUDE
5  /CRITERIA ALPHA=0.05  CILEVEL=95.

نتیجه اجرای این آزمون در پنجره خروجی Output به شکل زیر خواهد بود.

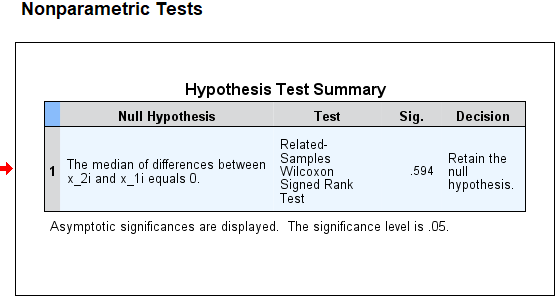
wilcoxon test in spss modern dialog output

همانطور که در ستون Decision جدول Hypothesis Test Summary دیده می‌شود، عبارت Retain the null hypothesis نشانگر تایید فرض صفر است. اگر بر روی این خروجی دوبار کلیک کنید، پنجره Model Viewer یا نمایشگر مدل نرم‌افزار SPSS نمایش داده شده و می‌توانید اطلاعات بیشتری هم دریافت کنید. در تصویر زیر این پنجره نمایش داده شده و قسمت‌های مختلف آن مشخص شده است.

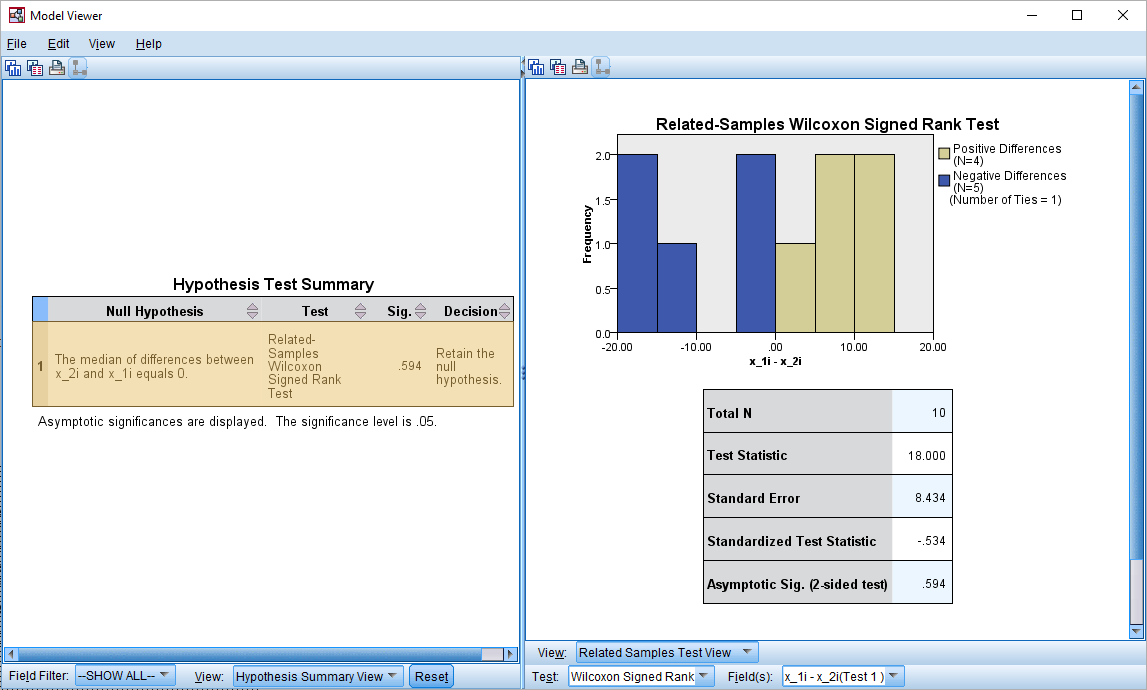
wilcoxon test in spss modern dialog model viewer

همانطور که در کادر سمت راست می‌بینید رتبه‌های منفی و مثبت مربوط به دو متغیر به همراه مجموع رتبه‌های علامت‌دار منفی (Test Statistics) ظاهر شده است. مقدار احتمال مجانبی Asymptotic Sig برای آزمون دو طرفه نیز در انتهای جدول دیده می‌شود. با توجه به مقدارها مشخص است که فرض صفر رد نخواهد شد. همچنین اگر گزینه View در کادر سمت راست را به Continuous Filed Information تغییر دهید، می‌توانید خصوصیات هر یک از متغیرها را به صورت یک نمودار فراوانی به همراه شاخص‌های آمار توصیفی به مانند تعداد (N)، حداقل (Min)، حداکثر (Max)، میانگین (Mean) و انحراف معیار (Std. Dev) نمایش دهید. در تصویر زیر این خصوصیات برای متغیر $$x_{2i}$$ نشان داده شده است.

continuous field information

خلاصه

آزمون‌های برمبنای رتبه‌ها برای اندازه نمونه‌های کوچک به کار می‌رود. همچنین اگر چولگی برای داده‌ها زیاد باشد بطوری که نتوان توزیع داده‌ها را نرمال یا گاوسی فرض کرد، آزمون‌های ناپارامتری نسبت به مشابه پارامتری خود از توان بیشتری برخوردارند در حالیکه با وجود توزیع نرمال برای داده‌ها، استفاده از آزمون‌های پارامتری، توان آزمون بیشتری به همراه دارد. ولی به هر حال از آنجایی که شرط توزیع برای آزمون‌های ناپارامتری وجود ندارد، بدون بررسی شرط‌ نرمال بودن داده‌ها می‌توان از آن‌ها استفاده کرد ولی نباید انتظار توان آزمون زیادی از آن‌ها داشت.

در میان آزمون‌های ناپارامتری نیز ممکن است بعضی از روش‌ها دارای توان آزمون بیشتری باشند. برای مثال توان آزمون علامت نسبت به آزمون من ویتنی کمتر است. از طرفی ممکن است داده‌ها نمونه تصادفی به صورت رتبه‌ای باشند، بنابراین در چنین مواقعی استفاده از آزمون‌های پارامتری امکان‌پذیر نیست.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

بر اساس رای ۲۲ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

آرمان ری بد (+)

«آرمان ری‌بد» دکتری آمار در شاخه آمار ریاضی دارد. از علاقمندی‌های او، یادگیری ماشین، خوشه‌بندی و داده‌کاوی است و در حال حاضر نوشتارهای مربوط به آمار و یادگیری ماشین را در مجله فرادرس تهیه می‌کند.