معرفی تکنیک های مرتب سازی (Sorting Techniques) — ساختار داده و الگوریتم ها

منظور از مرتب سازی داده، چیدمان داده‌ها در قالبی خاص است. الگوریتم مرتب سازی روشی برای چیدمان داده‌ها با ترتیبی خاص تعیین می‌کند. اغلب ترتیب‌های رایج به صورت ترتیب عددی یا الفبایی هستند. اهمیت مرتب سازی در این نکته است که جستجوی داده‌ها در صورت مرتب بودن می‌تواند تا سطح بالایی بهینه‌سازی شود. مرتب سازی همچنین می‌تواند برای نمایش داده‌ها در قالب‌های خواناتر کمک کند. در ادامه نمونه‌هایی از کاربردهای مرتب سازی در زندگی روزمره ارائه شده است:

• دفترچه تلفن: دفترچه تلفن حاوی شماره تلفن‌های افراد است که بر اساس نام‌هایشان مرتب سازی شده است تا بتوان نام‌ها را به راحتی جستجو کرد.
• فرهنگ لغت: فرهنگ لغت حاوی واژگانی است که با ترتیب الفبایی مرتب شده‌اند تا جستجوی هر کلمه آسان باشد.

مرتب سازی در جا و مرتب سازی غیر در جا

الگوریتم‌های مرتب سازی برای مقایسه و ذخیره‌سازی موقت عناصر داده‌ای ممکن است به فضای اضافی نیاز داشته باشند. الگوریتم‌هایی که برای مرتب سازی به فضای اضافی نیاز ندارند، به نام الگوریتم‌های مرتب سازی در جا نامیده می‌شوند و از فضای خود آرایه بدین منظور استفاده می‌کنند. این روش مرتب سازی در جا نامیده می‌شود. برای نمونه مرتب سازی حبابی یک نمونه از الگوریتم‌های مرتب سازی در جا است.

با این حال در برخی الگوریتم‌های مرتب سازی برنامه نیازمند فضایی است که معادل تعداد عناصر مورد مرتب سازی یا بیشتر از آن است. الگوریتم‌های مرتب سازی که نیازمند فضای معادل خود آرایه و یا بیشتر از آن هستند به نام الگوریتم‌های مرتب سازی غیر در جا نامیده می‌شوند. برای نمونه الگوریتم مرتب سازی ادغامی یک الگوریتم مرتب سازی غیر در جا است.

مرتب سازی پایدار و غیر پایدار

اگر یک الگوریتم مرتب سازی پس از مرتب کردن محتوا، توالی عناصر مشابه را تغییر ندهد به نام الگوریتم مرتب سازی پایدار نامیده می‌شود.

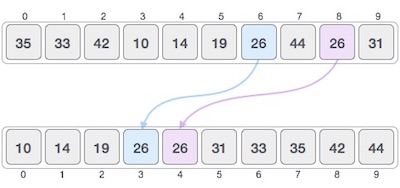
اگر یک الگوریتم مرتب سازی پس از مرتب کردن محتوا، توالی عناصر مشابه را تغییر دهد به نام الگویتم مرتب سازی غیر پایدار نامیده می‌شوند:

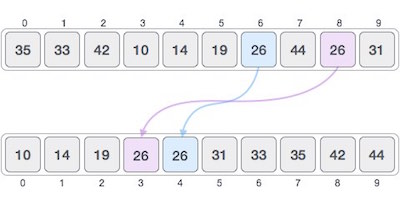
زمانی که می‌خواهیم توالی عناصر اصلی را حفظ کنیم، مثلاً در مورد مرتب سازی چندتایی‌ها، پایداری یک الگوریتم اهمیت خواهد یافت.

الگوریتم مرتب سازی تطبیقی و غیر تطبیقی

یک الگوریتم مرتب سازی در صورتی تطبیقی نامیده می‌شود که از مزیت عناصر قبلاً مرتب شده در ساختار دادهای که می‌خواهد مرتب سازی کند، بهره بگیرد. یعنی این الگوریتم هنگامی که می‌خواهد یک فهرست را مرتب کند، بررسی می‌کند و در صورتی که برخی عناصر موجود از قبل مرتب باشند، از این خصوصیت استفاده می‌کند و ترتیب این عناصر را تغییر نمی‌دهد.

الگوریتم مرتب سازی غیر تطبیقی الگوریتمی است که به ترتیب کنونی عناصر اهمیتی نمی‌دهد. این الگوریتم‌ها تلاش می‌کنند ترتیب تک تک عناصر را تغییر دهند تا ترتیب نهایی مطلوب را به دست آورند.

اصطلاح‌های مهم

برخی اصلاح‌ها به طور کلی در مباحث مرتبط با تکنیک‌های مرتب سازی بیشتر به چشم می‌آیند که در ادامه برخی از آن‌ها را ارائه کرده‌ایم:

ترتیب صعودی

یک توالی از مقادیر مختلف، زمانی دارای ترتیب صعودی نامیده می‌شود که همه عناصر پشت سر هم بزرگ‌تر از عنصر قبلی‌شان باشند. برای نمونه فهرست 1، 3، 4، 8، 9 دارای ترتیب صعودی است چون هر عنصر از عنصر قبلی خود بزرگ‌تر است.

ترتیب نزولی

یک توالی از مقادیر، زمانی دارای ترتیب نزولی خوانده می‌شود که همه عناصر پشت سر هم از عنصر قبلی خود کوچک‌تر باشند. برای نمونه، 9، 8، 6، 4، 3، 1 دارای ترتیب نزولی است و هر عنصر از عنصر قبلی خود کوچک‌تر است.

ترتیب غیر افزایشی

یک توالی از مقادیر دارای ترتیب غیر افزایشی نامیده می‌شود، وقتی همه عناصر پشت سر هم کمتر یا مساوی عنصر قبلی‌شان باشند. این ترتیب زمانی رخ می‌دهد که در توالی مقادیر مورد نظر، عناصری تکراری وجود داشته باشند. برای نمونه، 9، 8، 6، 3، 3، 1 دارای ترتیب غیر افزایشی است، چون هر عنصر کوچک‌تر یا مساوی (در مورد 3) از عنصر قبلی است، اما هیچ عنصری از عنصر قبلی خود بزرگ‌تر نیست.

ترتیب غیر کاهشی

یک توالی از مقادیر، دارای ترتیب غیر کاهشی خوانده می‌شود، اگر عناصر پشت سر هم همواره بزرگ‌تر یا مساوی عنصر قبلی‌شان باشند. این ترتیب زمانی رخ می‌دهد که در یک توالی عناصر تکراری وجود داشته باشد. برای نمونه لیست 1، 3، 3، 6، 8، 9 یک فهرست با ترتیب غیر کاهشی است، چون هر عنصر کوچک‌تر یا مساوی (در مورد 3) از عنصر قبلی است؛ اما بزرگ‌تر نیست.

الگوریتم مرتب سازی حبابی (Bubble Sort)

مرتب سازی حبابی یک الگوریتم مرتب سازی ساده است. این الگوریتم مرتب سازی یک الگوریتم مبتنی بر مقایسه است که در آن هر جفت از عناصر مجاور با هم مقایسه می‌شوند و در صورتی که در ترتیب مطلوب نباشند با هم تعویض می‌شوند. این الگوریتم برای مجموعه داده‌های بزرگ مطلوب نیست، زیرا پیچیدگی حالت میانگین و بدترین حالت آن برابر با (Ο(n2 است که در آن n تعداد آیتم‌هایی است که باید مرتب شوند.

طرز کار مرتب سازی حبابی

به عنوان مثال یک آرایه نامرتب را در نظر می‌گیریم. الگوریتم مرتب سازی حبابی باید (Ο(n2 مرتبه روی این آرایه کار کند تا آن را مرتب و منظم کند

مرتب سازی حبابی کار خود را با نخستین دو عنصر آغاز می‌کند و آن‌ها را مقایسه می‌کند تا ببیند کدام یک بزرگ‌تر است:

در این مثال 33 از 14 بزرگ‌تر است و از این رو این دو عنصر هم‌اینک در وضعیت مرتب هستند، سپس دو مقدار 33 و 27 را مقایسه می‌کنیم:

درمی‌یابیم که 27 کوچک‌تر از 33 است و لذا موقعیت این دو عنصر باید تعویض شود.

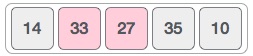
اینک آرایه به صورت زیر درمی‌آید:

سپس 33 و 35 را مقایسه می‌کنیم. مشخص است که این دو مقدار در وضعیت مرتب هستند.

سپس دو مقدار بعدی یعنی 35 و 10 مقایسه می‌شوند

می‌دانیم که 10 کوچک‌تر از 35 است. از این رو این دو مقدار مرتب نیستند.

این دو مقدار را تعویض می‌کنیم. درمی‌یابیم که به انتهای آرایه رسیده‌ایم. پس از یک چرخه، آرایه به صورت زیر درمی‌آید:

برای این که فرایند کار را خلاصه کنیم وضعیت آرایه را پس از هر چرخه مرتب سازی در ادامه ارائه کرده‌ایم. پس از چرخه دوم آرایه به صورت زیر درمی‌آید:

توجه کنید که پس از هر چرخه، دست کم یک مقدار تغییر یافته است

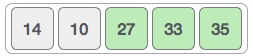
و زمانی که دیگر هیچ تعویضی رخ ندهد، الگوریتم مرتب سازی حبابی می‌فهمد که آرایه به طور کامل مرتب شده است.

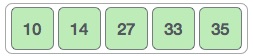
الگوریتم مرتب‌سازی حبابی بسیار شبیه به الگوریتم مرتب سازی تعویضی است. اینک الگوریتم مرتب سازی حبابی را به صورت عملی بررسی می‌کنیم:

الگوریتم

فرض می‌کنیم که list آرایه‌ای با n عنصر باشد. همچنین فرض می‌کنیم که تابع swap مقادیر مفروض عناصر آرایه را با هم تعویض کند.

begin BubbleSort(list)

   for all elements of list
      if list[i] > list[i+1]
         swap(list[i], list[i+1])
      end if
   end for
   
   return list
   
end BubbleSort

شبه کد

در الگوریتم مشاهده کردیم که مرتب سازی حبابی هر جفت از عناصر آرایه را مرتب می‌کند تا این که کل آرایه در ترتیب نزولی مرتب شده باشد. این وضعیت ممکن است موجب بروز برخی مشکل‌ها در خصوص پیچیدگی شود، مثلاً اگر به دلیل این که همه عناصر از قبل دارای ترتیب نزولی باشند، و نیازی به تعویض عناصر آرایه نباشد، چه اتفاقی می‌افتد؟ شبه کد الگوریتم مرتب سازی حبابی را به صورت زیر می‌توان نوشت:

procedure bubbleSort( list : array of items )

   loop = list.count;
   
   for i = 0 to loop-1 do:
      swapped = false
		
      for j = 0 to loop-1 do:
      
         /* compare the adjacent elements */   
         if list[j] > list[j+1] then
            /* swap them */
            swap( list[j], list[j+1] )		 
            swapped = true
         end if
         
      end for
      
      /*if no number was swapped that means 
      array is sorted now, break the loop.*/
      
      if(not swapped) then
         break
      end if
      
   end for
   
end procedure return list

پیاده‌سازی

یک مشکل دیگر که در الگوریتم خودمان رفع نکردیم ولی در شبه کد بهینه‌سازی شده وجود دارد، این است که پس از هر چرخه، بزرگ‌ترین مقادیر در انتهای آرایه قرار می‌گیرند. از این رو در چرخه بعدی لازم نیست عناصری که قبلاً مرتب سازی شده‌اند دوباره بررسی شوند. به این منظور در پیاده‌سازی خودمان حلقه داخلی را محدود ساخته‌ایم تا از مقادیر قبلاً مرتب شده اجتناب کند.

پیاده‌سازی الگوریتم مرتب سازی حبابی در زبان C

#include 
#include 

#define MAX 10

int list[MAX] = {1,8,4,6,0,3,5,2,7,9};

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0; i < MAX; i++) {
      printf("%d ",list[i]);
   }
	
   printf("]\n");
}

void bubbleSort() {
   int temp;
   int i,j;
	
   bool swapped = false;
   
   // loop through all numbers 
   for(i = 0; i < MAX-1; i++) { 
      swapped = false;
		
      // loop through numbers falling ahead 
      for(j = 0; j < MAX-1-i; j++) { printf(" Items compared: [ %d, %d ] ", list[j],list[j+1]); // check if next number is lesser than current no // swap the numbers. // (Bubble up the highest number) if(list[j] > list[j+1]) {
            temp = list[j];
            list[j] = list[j+1];
            list[j+1] = temp;

            swapped = true;
            printf(" => swapped [%d, %d]\n",list[j],list[j+1]);
         } else {
            printf(" => not swapped\n");
         }
			
      }

      // if no number was swapped that means 
      //   array is sorted now, break the loop. 
      if(!swapped) {
         break;
      }
      
      printf("Iteration %d#: ",(i+1)); 
      display();
   }
	
}

void main() {
   printf("Input Array: ");
   display();
   printf("\n");
	
   bubbleSort();
   printf("\nOutput Array: ");
   display();
}

اگر کد فوق را کامپایل و اجرا کنیم، خروجی زیر حاصل می‌شود:

خروجی

Input Array: [1 8 4 6 0 3 5 2 7 9 ]
     Items compared: [ 1, 8 ]  => not swapped
     Items compared: [ 8, 4 ]  => swapped [4, 8]
     Items compared: [ 8, 6 ]  => swapped [6, 8]
     Items compared: [ 8, 0 ]  => swapped [0, 8]
     Items compared: [ 8, 3 ]  => swapped [3, 8]
     Items compared: [ 8, 5 ]  => swapped [5, 8]
     Items compared: [ 8, 2 ]  => swapped [2, 8]
     Items compared: [ 8, 7 ]  => swapped [7, 8]
     Items compared: [ 8, 9 ]  => not swapped
Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ]
     Items compared: [ 1, 4 ]  => not swapped
     Items compared: [ 4, 6 ]  => not swapped
     Items compared: [ 6, 0 ]  => swapped [0, 6]
     Items compared: [ 6, 3 ]  => swapped [3, 6]
     Items compared: [ 6, 5 ]  => swapped [5, 6]
     Items compared: [ 6, 2 ]  => swapped [2, 6]
     Items compared: [ 6, 7 ]  => not swapped
     Items compared: [ 7, 8 ]  => not swapped
Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ]
     Items compared: [ 1, 4 ]  => not swapped
     Items compared: [ 4, 0 ]  => swapped [0, 4]
     Items compared: [ 4, 3 ]  => swapped [3, 4]
     Items compared: [ 4, 5 ]  => not swapped
     Items compared: [ 5, 2 ]  => swapped [2, 5]
     Items compared: [ 5, 6 ]  => not swapped
     Items compared: [ 6, 7 ]  => not swapped
Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ]
     Items compared: [ 1, 0 ]  => swapped [0, 1]
     Items compared: [ 1, 3 ]  => not swapped
     Items compared: [ 3, 4 ]  => not swapped
     Items compared: [ 4, 2 ]  => swapped [2, 4]
     Items compared: [ 4, 5 ]  => not swapped
     Items compared: [ 5, 6 ]  => not swapped
Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ]
     Items compared: [ 0, 1 ]  => not swapped
     Items compared: [ 1, 3 ]  => not swapped
     Items compared: [ 3, 2 ]  => swapped [2, 3]
     Items compared: [ 3, 4 ]  => not swapped
     Items compared: [ 4, 5 ]  => not swapped
Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ]
     Items compared: [ 0, 1 ]  => not swapped
     Items compared: [ 1, 2 ]  => not swapped
     Items compared: [ 2, 3 ]  => not swapped
     Items compared: [ 3, 4 ]  => not swapped

Output Array: [0 1 2 3 4 5 6 7 8 9 ]

الگوریتم مرتب سازی درجی (Insertion Sort)

الگوریتم مرتب سازی درجی یک الگوریتم مرتب سازی مبتنی بر مقایسه است. در این روش یک لیست فرعی نگه‌داری می‌شود که همواره در وضعیت مرتب است. برای نمونه بخش پایینی یک آرایه در وضعیت مرتب حفظ می‌شود. عنصری که باید در این لیست فرعی مرتب درج شود، می‌بایست موقعیت مناسب خود را بیابد و سپس در آنجا درج شود. از این رو نام این الگوریتم، مرتب سازی درجی است.

آرایه به طور ترتیبی جستجو می‌شود و آیتم‌های مرتب نشده جابجا شده و در لیست فرعی مرتب (در همان آرایه) درج می‌شوند. این الگوریتم برای مجموعه داده‌های بزرگ مناسب نیست، چون پیچیدگی سناریوهای حالت میانگین و بدترین حالت آن برابر با (Ο(n2 است که منظور از n تعداد آیتم‌ها است.

طرز کار الگوریتم مرتب سازی درجی

برای مثال یک آرایه نامرتب را در نظر می‌گیریم.

مرتب سازی درجی دو عنصر اول را مقایسه می‌کند:

مشخص است که هر دو مقدار 14 و 33 از قبل در ترتیب صعودی هستند. بنابراین 14 در لیست فرعی درج می‌شود.

مرتب سازی درجی پیش می‌رود و مقادیر 33 و 27 را مقایسه می‌کند.

و در می‌یابد که 33 در موقعیت صحیحی قرار ندارد.

الگوریتم موقعیت مقدار 33 را با مقدار 27 تعویض می‌کند. همچنین ترتیب آن را با همه عناصر لیست فرعی بررسی می‌کند. در این جا می بنیم که لیست فرعی مرتب شده تنها عناصر 14 و 27 را دارد که بزرگ‌تر از 14 هستند. از این رو لیست فرعی مرتب شده پس از این جابجایی همچنان در وضعیت مرتب است.

اینک مقادیر 14 و 27 را در لیست فرعی مرتب داریم. سپس مقادیر 33 و 10 را مقایسه می‌کنیم.

این مقادیر در ترتیب صحیحی نیستند.

موقعیت آن‌ها را تعویض می‌کنیم.

با این حال تعویض موقعیت‌ها باعث می‌شود که 27 و 10 از وضعیت مرتب خارج شوند.

از این رو آها را نیز تعویض می‌کنیم

باز درمی‌یابیم که 14 و 10 نیز در ترتیب ناصحیحی هستند:

آن‌ها را نیز تعویض می‌کنیم. در نهایت ما اینک یک لیست فرعی مرتب با 4 آیتم داریم.

این فرایند تا زمانی که همه مقادیر نامرتب در لیست فرعی مرتب قرار گیرند ادامه می‌یابد. در ادامه جنبه‌های برنامه‌نویسی مرتب سازی درجی را بررسی می‌کنیم.

الگوریتم

اینک تصویر دقیقی از شیوه عمل این الگوریتم مرتب سازی درجی داریم و می‌توانیم مراحل ساده‌ای که برای رسیدن به این نوع مرتب سازی لازم است را نتیجه بگیریم:

• گام 1 – اگر عنصر اول آرایه را بررسی می‌کنی و از قبل مرتب است، مقدار 1 را بازگشت بده
• گام 2 – عنصر بعدی را انتخاب کن
• گام 3 – عنصر انتخابی را با همه عناصر لیست فرعی مرتب مقایسه کن
• گام 4 – همه عناصری که در لیست فرعی مرتب هستند و بزرگ‌تر از مقدار مورد نظر هستند را جابجا کن تا کل لیست فرعی مرتب شود.
• گام 5 – مقدار را در موقعیت مطلوب در لیست فرعی وارد کن
• گام 6 – تا زمانی که همه لیست مرتب شوند ادامه بدهد

شبه کد

procedure insertionSort( A : array of items )
   int holePosition
   int valueToInsert
	
   for i = 1 to length(A) inclusive do:
	
      /* select value to be inserted */
      valueToInsert = A[i]
      holePosition = i
      
      /*locate hole position for the element to be inserted */
		
      while holePosition > 0 and A[holePosition-1] > valueToInsert do:
         A[holePosition] = A[holePosition-1]
         holePosition = holePosition -1
      end while
		
      /* insert the number at hole position */
      A[holePosition] = valueToInsert
      
   end for
	
end procedure

پیاده‌سازی الگوریتم مرتب سازی درجی در زبان C

#include 
#include 

#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
   int i;
	
   for(i = 0;i < count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i < MAX;i++) {
      printf("%d ",intArray[i]);
   }
	
   printf("]\n");
}

void insertionSort() {

   int valueToInsert;
   int holePosition;
   int i;
  
   // loop through all numbers 
   for(i = 1; i < MAX; i++) { // select a value to be inserted. valueToInsert = intArray[i]; // select the hole position where number is to be inserted holePosition = i; // check if previous no. is larger than value to be inserted while (holePosition > 0 && intArray[holePosition-1] > valueToInsert) {
         intArray[holePosition] = intArray[holePosition-1];
         holePosition--;
         printf(" item moved : %d\n" , intArray[holePosition]);
      }

      if(holePosition != i) {
         printf(" item inserted : %d, at position : %d\n" , valueToInsert,holePosition);
         // insert the number at hole position 
         intArray[holePosition] = valueToInsert;
      }

      printf("Iteration %d#:",i);
      display();
		
   }  
}

void main() {
   printf("Input Array: ");
   display();
   printline(50);
   insertionSort();
   printf("Output Array: ");
   display();
   printline(50);
}

اگر کد فوق را کامپایل کرده و اجرا کنید، خروجی زیر را مشاهده می‌کنید:

خروجی

Input Array: [4 6 3 2 1 9 7 ]
==================================================
Iteration 1#:[4 6 3 2 1 9 7 ]
 item moved : 6
 item moved : 4
 item inserted : 3, at position : 0
Iteration 2#:[3 4 6 2 1 9 7 ]
 item moved : 6
 item moved : 4
 item moved : 3
 item inserted : 2, at position : 0
Iteration 3#:[2 3 4 6 1 9 7 ]
 item moved : 6
 item moved : 4
 item moved : 3
 item moved : 2
 item inserted : 1, at position : 0
Iteration 4#:[1 2 3 4 6 9 7 ]
Iteration 5#:[1 2 3 4 6 9 7 ]
 item moved : 9
 item inserted : 7, at position : 5
Iteration 6#:[1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================

الگوریتم مرتب سازی انتخابی (Selection sort)

مرتب سازی انتخابی یک الگوریتم مرتب سازی ساده است. این الگوریتم مرتب سازی یک روش مرتب سازی درجا و مبتنی بر مقایسه است که در آن لیست به دو بخش تقسیم می‌شود، بخش مرتب در سمت چپ و بخش نامرتب در سمت راست قرار می‌گیرد. در ابتدا بخش مرتب خالی است و بخش نامرتب کل لیست را شامل می‌شود.

کوچک‌ترین عنصر از آرایه نامرتب انتخاب می‌شود و با عنصری که در انتهای سمت چپ قرار دارد تعویض می‌شود. این فرایند تا زمانی که به کران سمت راست آرایه برسیم ادامه می‌یابد.

این الگوریتم برای مجموعه داده‌های بزرگ مناسب نیست چون پیچیدگی سناریوهای حالت متوسط و بدترین حالت آن برابر با (Ο(n2 است که در آن n تعداد آیتم‌های آرایه است.

طرز کار الگوریتم مرتب سازی انتخابی

آرایه‌ای که در تصویر زیر نشان داده شده را در نظر بگیرید:

برای این که دو عنصر اولیه لیست مرتب باشند، باید همه لیست به صورت ترتیبی بررسی شوند. موقعیت نخست حاوی مقدار 14 است که در حال حاضر در وضعیت مرتب قرار دارد، کل لیست را جستجو می‌کنیم و درمی‌یابیم که 10 مقدار کمتری دارد:

بنابراین جای 14 و 10 را عوض می‌کنیم. پس از چرخه نخست مشخص می‌شود که 10 کوچک‌ترین عنصر لیست است و در موقعیت ابتدایی لیست مرتب قرار می‌گیرد.

برای موقعیت دوم که اینک مقدار 33 را در خود جای داده، باقی مانده لیست را به همان روش خطی بررسی می‌کنیم.

درمی‌یابیم که 14 دومین مقدار کوچک در آرایه ما است و باید در جایگاه دوم لیست قرار داشته باشد، این مقادیر را تعویض می‌کنیم

پس از چرخه دوم اینک دو مقدار داریم که در ابتدای لیست به صورت مرتب قرار گرفته‌اند:

همین فرایند در مورد بخش باقی مانده لیست نیز به کار گرفته می‌شود. در ادامه کل فرایند مرتب سازی به صورت مرحله به مرحله و تصویری ارائه شده است:

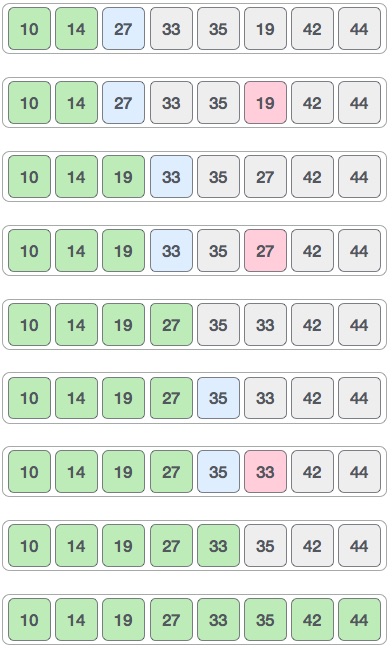
اینک جنبه‌های برنامه‌نویسی الگوریتم مرتب سازی انتخابی را بررسی می‌کنیم:

الگوریتم

• گام 1 – مقدار Min را برابر با 0 می‌گیریم.
• گام 2 - به دنبال کوچک‌ترین عنصر لیست می‌گردیم.
• گام 3 – کوچک‌ترین مقدار را در موقعیت Min قرار می‌دهیم
• گام 4 – مقدار Min را به افزایش می‌دهیم تا برابر با این مقدار جدید باشد.
• گام 5- این فرایند را تا زمانی که همه لیست مرتب شود تکرار می‌کنیم.

شبه کد

procedure selection sort 
   list  : array of items
   n     : size of list

   for i = 1 to n - 1
   /* set current element as minimum*/
      min = i    
  
      /* check the element to be minimum */

      for j = i+1 to n 
         if list[j] < list[min] then
            min = j;
         end if
      end for

      /* swap the minimum element with the current element*/
      if indexMin != i  then
         swap list[min] and list[i]
      end if
   end for
	
end procedure

پیاده‌سازی الگوریتم مرتب سازی انتخابی در زبان C

#include 
#include 

#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
   int i;
	
   for(i = 0;i < count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i < MAX;i++) {
      printf("%d ", intArray[i]);
   }
	
   printf("]\n");
}

void selectionSort() {
   int indexMin,i,j;
	
   // loop through all numbers 
   for(i = 0; i < MAX-1; i++) { 
	
      // set current element as minimum 
      indexMin = i;
		
      // check the element to be minimum 
      for(j = i+1;j < MAX;j++) {
         if(intArray[j] < intArray[indexMin]) {
            indexMin = j;
         }
      }

      if(indexMin != i) {
         printf("Items swapped: [ %d, %d ]\n" , intArray[i], intArray[indexMin]); 
			
         // swap the numbers 
         int temp = intArray[indexMin];
         intArray[indexMin] = intArray[i];
         intArray[i] = temp;
      }          

      printf("Iteration %d#:",(i+1));
      display();
   }
}  

void main() {
   printf("Input Array: ");
   display();
   printline(50);
   selectionSort();
   printf("Output Array: ");
   display();
   printline(50);
}

اگر کد فوق را کامپایل و اجرا کنیم، خروجی زیر به دست می‌آید:

خروجی

Input Array: [4 6 3 2 1 9 7 ]
==================================================
Items swapped: [ 4, 1 ]
Iteration 1#:[1 6 3 2 4 9 7 ]
Items swapped: [ 6, 2 ]
Iteration 2#:[1 2 3 6 4 9 7 ]
Iteration 3#:[1 2 3 6 4 9 7 ]
Items swapped: [ 6, 4 ]
Iteration 4#:[1 2 3 4 6 9 7 ]
Iteration 5#:[1 2 3 4 6 9 7 ]
Items swapped: [ 9, 7 ]
Iteration 6#:[1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================

الگوریتم مرتب سازی ادغامی (Merge sort)

مرتب سازی ادغامی تکنیکی است که بر مبنای الگوریتم حل مسئله «تقسیم و حل» عمل می‌کند. پیچیدگی بدترین حالت برای این الگوریتم برابر با (Ο(n log n است و از این رو یکی از الگوریتم‌هایی است که بسیار مورد استقبال قرار می‌گیرد.

مرتب سازی ادغامی، ابتدا آرایه را به دو نیمه مساوی تقسیم می‌کند و سپس آن‌ها را به روشی مرتب با هم ترکیب می‌کند.

طرز کار مرتب سازی ادغامی

برای درک مرتب سازی ادغامی یک آرایه نامرتب را به صورت زیر در نظر می‌گیریم:

می‌دانیم که مرتب سازی ادغامی نخست کل آرایه را به نیمه‌های مساوی تقسیم می‌کند تا این که به مقادیر منفرد برسد. در ادامه می‌بینیم که یک آرایه 8 آیتمی به دو آرایه 4 تایی تقسیم می‌شود.

این کار توالی نمایش آیتم‌ها را در آرایه اصلی تغییر نمی‌دهد. اینک می‌توانیم این دو آرایه را به دو نیمه تقسیم کنیم.

در مرحله بعد باز هم آرایه‌ها را به دو نیمه تقسیم می‌کنیم و بدین ترتیب 8 مقدار منفرد به دست می‌آید که دیگر قابل تقسیم نیستند.

اینک آن‌ها را به همان روشی که تقسیم کردیم، با هم ترکیب می‌کنیم. لطفاً به کدهای رنگی که به عناصر داده شده است، توجه کنید.

در ابتدا عناصر هر لیست را مقایسه می‌کنیم و سپس آن را به روش مرتب در یک لیست دیگر ترکیب می‌کنیم. می‌بینیم که 14 و 33 در موقعیت‌های مرتب هستند. مقادیر 27 و 10 را مقایسه کرده و در لیست هدف 2 مقداری آن‌ها را به روش مرتب درج می‌کنیم، یعنی ابتدا 10 و سپس 27. بدین ترتیب در ادامه موقعیت‌های 19 و 35 را نیز عوض می‌کنیم در حالی که 42 و 44 به همان ترتیب در لیست 2 تایی جای می‌گیرند.

در چرخه بعدی از فاز ترکیب، لیست‌های 2 مقداری را با هم مقایسه می‌کنیم و آن‌ها را در دو لیست چهارتایی ترکیب می‌کنیم به طوری که همه عناصر به صورت مرتب باشند.

پس از ادغام نهایی، لیست به صورت زیر درمی‌آید:

در ادامه برخی جنبه‌های برنامه‌نویسی مرتب سازی ادغامی را با هم مرور می‌کنیم.

الگوریتم

مرتب سازی ادغامی به طور مداوم لیست را به نیمه‌های مساوی تقسیم می‌کند، تا جایی که دیگر امکان تقسیم نباشد. بر اساس تعریف اگر لیستی تنها یک آیتم داشته باشد، این لیست مرتب محسوب می‌شود. بنابراین مرتب سازی ادغامی این لیست‌های مرتب کوچک‌تر را به ترتیب با هم دیگر ادغام می‌کند، به طوری که لیست حاصل هم مرتب باشد.

• گام 1 – اگر تنها یک عنصر در لیست باشد، این لیست مرتب است و بازگرد.
• گام 2- لیست را به طور بازگشتی به نیمه‌های مساوی تقسیم کن تا زمانی که دیگر امکان تقسیم وجود نداشته باشد.
• گام 3- لیست‌های کوچک‌تر را به روشی مرتب در یک لیست جدید ادغام کن.

شبه کد

در ادامه شبه کد الگوریتم مرتب سازی ادغامی را می‌بینیم. توجه کنید که الگوریتم ما دارای دو تابع اصلی است: تقسیم و ادغام. مرتب سازی ادغامی به صورت بازگشتی عمل می‌کند و پیاده‌سازی ما نیز به همین ترتیب بوده است:

procedure mergesort( var a as array )
   if ( n == 1 ) return a

   var l1 as array = a[0] ... a[n/2]
   var l2 as array = a[n/2+1] ... a[n]

   l1 = mergesort( l1 )
   l2 = mergesort( l2 )

   return merge( l1, l2 )
end procedure

procedure merge( var a as array, var b as array )

   var c as array
   while ( a and b have elements )
      if ( a[0] > b[0] )
         add b[0] to the end of c
         remove b[0] from b
      else
         add a[0] to the end of c
         remove a[0] from a
      end if
   end while
   
   while ( a has elements )
      add a[0] to the end of c
      remove a[0] from a
   end while
   
   while ( b has elements )
      add b[0] to the end of c
      remove b[0] from b
   end while
   
   return c
	
end procedure

پیاده‌سازی الگوریتم مرتب سازی ادغامی در زبان C

#include 

#define max 10

int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];

void merging(int low, int mid, int high) {
   int l1, l2, i;

   for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
      if(a[l1] <= a[l2])
         b[i] = a[l1++];
      else
         b[i] = a[l2++];
   }
   
   while(l1 <= mid)    
      b[i++] = a[l1++];

   while(l2 <= high)   
      b[i++] = a[l2++];

   for(i = low; i <= high; i++)
      a[i] = b[i];
}

void sort(int low, int high) {
   int mid;
   
   if(low < high) {
      mid = (low + high) / 2;
      sort(low, mid);
      sort(mid+1, high);
      merging(low, mid, high);
   } else { 
      return;
   }   
}

int main() { 
   int i;

   printf("List before sorting\n");
   
   for(i = 0; i <= max; i++)
      printf("%d ", a[i]);

   sort(0, max);

   printf("\nList after sorting\n");
   
   for(i = 0; i <= max; i++)
      printf("%d ", a[i]);
}

اگر کد فوق را کامپایل و اجرا کنیم، نتیجه زیر را مشاهده خواهیم کرد:

خروجی

List before sorting

10 14 19 26 27 31 33 35 42 44 0

List after sorting

0 10 14 19 26 27 31 33 35 42 44

الگوریتم مرتب سازی شِل (Shell sort)

مرتب سازی شل یکی از الگوریتم‌های مرتب سازی بسیار بهینه است که بر مبنای الگوریتم مرتب سازی درجی عمل می‌کند. این الگوریتم از جابجایی‌های بزرگی که در آن مقادیر کوچک‌تر در موقعیت‌های دورتر در سمت راست یا چپ قرار دارند و در مرتب سازی درجی وجود داشت، اجتناب می‌کند.

این الگوریتم از مرتب سازی درجی بر روی عناصر بسیار دور از هم استفاده می‌کند و ابتدا آن‌ها را مرتب سازی می‌کند و سپس عناصری که فاصله اندکی با هم دارند را مرتب می‌سازد. این فاصله‌گذاری به نام بازه (Interval) نامیده می‌شود. این بازه بر اساس فرمول نات (knuth) به صورت زیر محاسبه می‌شود:

فرمول نات

h = h * 3 + 1

که h بازه‌ای به اندازه 1 است.

این الگوریتم برای مجموعه داده‌های با اندازه متوسط بسیار بهینه است، زیرا سناریوی حالت متوسط آن دارای پیچیدگی (Ο(nlogn است که n تعداد آیتم‌های لیست است. توجه داشته باشید که بدترین حالت آن نیز برابر با Ο(n²) است.

طرز کار الگوریتم مرتب سازی شل

برای این که بهتر متوجه شویم مرتب سازی شل چگونه عمل می‌کند، مثال زیرا را در نظر بگیرید. برای سهولت کار مثالی که در بخش‌های قبلی بررسی کردیم را در نظر می‌گیریم. همچنین برای سادگی امور بازه را به اندازه 4 فرض می‌کنیم. یک لیست فرعی مجازی از همه مقادیری که در بازه‌ای به اندازه 4 واحد از هم قرار دارند را تصور می‌کنیم. در این بازه‌ها مقادیر {35 و 14}، {33 و 19}، {42 و 27} و {10 و 44} قرار دارند.

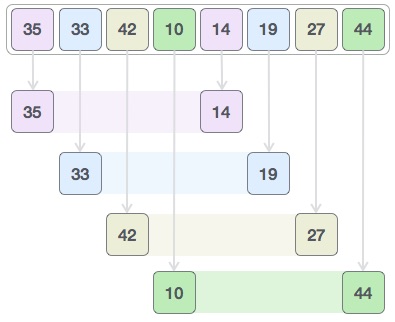
مقادیر هر لیست فرعی را با هم مقایسه می‌کنیم و آن‌ها را در صورت لزوم در آرایه اصلی با هم تعویض می‌کنیم. پس از این مرحله آرایه جدید به شکل زیر درمی‌آید:

سپس بازه 2 را در نظر می‌گیریم و این شکاف دو زیر لیست ایجاد می‌کند: {14, 27, 35, 42}, {19, 10, 33, 44}

ما این مقادیر را مقایسه کرده و در صورت لزوم در آرایه اصلی جابجا می‌کنیم. پس از این مرحله، آرایه ما به شکل زیر درمی‌آید:

در نهایت بخش‌های باقی مانده آرایه را با استفاده از بازه 1 مرتب می‌کنیم. مرتب سازی شل در این مرحله از مرتب سازی درجی برای مرتب سازی آرایه استفاده می‌کند.

در ادامه این فرایند به صورت گام به گام به تصویر کشیده شده است:

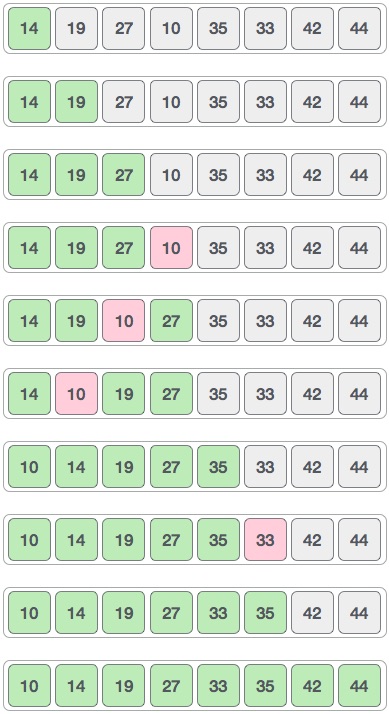
می‌بینیم که برای مرتب سازی بقیه آرایه تنها به 4 تکرار نیاز داریم.

الگوریتم

• گام 1- مقدار اولیه h را محاسبه کن
• گام 2- لیست را به زیرلیست‌های کوچک‌تر با بازه‌های مساوی h تقسیم کنید.
• گام 3- این زیرلیست‌ها را با استفاده از مرتب سازی درجی مرتب کن.
• گام 4 – تا زمانی که همه لیست مرتب شود این فرایند را تکرار کن

شبه کد

procedure shellSort()
   A : array of items 
	
   /* calculate interval*/
   while interval < A.length /3 do: interval = interval * 3 + 1 end while while interval > 0 do:

      for outer = interval; outer < A.length; outer ++ do: /* select value to be inserted */ valueToInsert = A[outer] inner = outer; /*shift element towards right*/ while inner > interval -1 && A[inner - interval] >= valueToInsert do:
            A[inner] = A[inner - interval]
            inner = inner - interval
         end while

      /* insert the number at hole position */
      A[inner] = valueToInsert

      end for

   /* calculate interval*/
   interval = (interval -1) /3;	  

   end while
   
end procedure

پیاده‌سازی الگوریتم مرتب سازی شل در زبان C

#include 
#include 

#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
   int i;
	
   for(i = 0;i < count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i < MAX;i++) {
      printf("%d ",intArray[i]);
   }
	
   printf("]\n");
}

void shellSort() {
   int inner, outer;
   int valueToInsert;
   int interval = 1;   
   int elements = MAX;
   int i = 0;
   
   while(interval <= elements/3) { interval = interval*3 +1; } while(interval > 0) {
      printf("iteration %d#:",i); 
      display();
      
      for(outer = interval; outer < elements; outer++) { valueToInsert = intArray[outer]; inner = outer; while(inner > interval -1 && intArray[inner - interval] 
            >= valueToInsert) {
            intArray[inner] = intArray[inner - interval];
            inner -=interval;
            printf(" item moved :%d\n",intArray[inner]);
         }
         
         intArray[inner] = valueToInsert;
         printf(" item inserted :%d, at position :%d\n",valueToInsert,inner);
      }
		
      interval = (interval -1) /3;
      i++;
   }          
}

int main() {
   printf("Input Array: ");
   display();
   printline(50);
   shellSort();
   printf("Output Array: ");
   display();
   printline(50);
   return 1;
}

اگر کد فوق را کامپایل و اجرا کنیم خروجی زیر حاصل می‌آید:

خروجی

Input Array: [4 6 3 2 1 9 7 ]
==================================================
iteration 0#:[4 6 3 2 1 9 7 ]
 item moved :4
 item inserted :1, at position :0
 item inserted :9, at position :5
 item inserted :7, at position :6
iteration 1#:[1 6 3 2 4 9 7 ]
 item inserted :6, at position :1
 item moved :6
 item inserted :3, at position :1
 item moved :6
 item moved :3
 item inserted :2, at position :1
 item moved :6
 item inserted :4, at position :3
 item inserted :9, at position :5
 item moved :9
 item inserted :7, at position :5
Output Array: [1 2 3 4 6 7 9 ]
==================================================

الگوریتم مرتب سازی سریع (Quick sort)

مرتب سازی سریع یک الگوریتم مرتب سازی بسیار بهینه است که بر اساس افراز یک آرایه به آرایه‌های کوچک‌تر عمل می‌کند. یک آرایه بزرگ به دو آرایه کوچک‌تر افراز می‌شود که یکی از آن‌ها مقادیری کوچک‌تر از یک مقدار مشخص را نگه‌داری می‌کند، فرض کنید این مقدار pivot نام دارد. بر همین اساس آرایه دیگر مقادیر بزرگ‌تر از Pivot را نگه‌داری می‌کند.

الگوریتم مرتب سازی سریع یک آرایه را افراز می‌کند و سپس خود را به صورت بازگشتی مجدداً فراخوانی می‌کند تا دو آرایه فرعی حاصل را مرتب سازی کند. این الگوریتم برای مجموعه داده‌های بزرگ کاملاً بهینه است، چون پیچیدگی سناریوی حالت متوسط برابر با ((Θ(n log(n و پیچیدگی زمانی بدترین حالت برابر با (Ο(n2 است که n تعداد آیتم‌ها است.

افراز در مرتب سازی سریع

در تصویر متحرک زیر روش یافتن مقدار pivot در آرایه را می‌بینید:

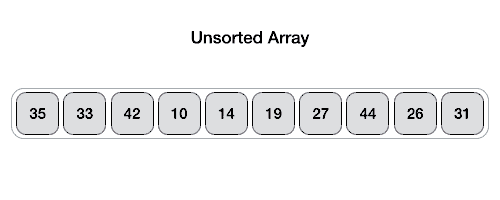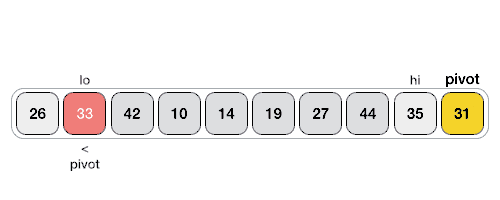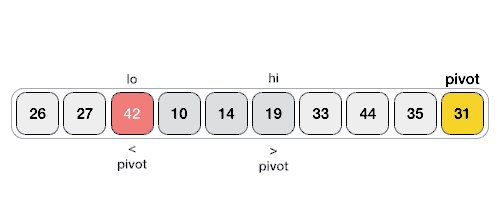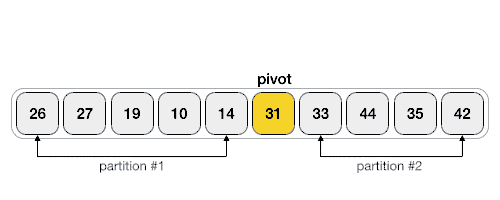
مقدار pivot لیست را به دو بخش تقسیم می‌کند و سپس به طور بازگشتی مقدار pivot را برای هر لیست فرعی پیدا می‌کنیم تا جایی که لیست‌ها تنها حاوی یک عنصر باشند.

الگوریتم pivot مرتب سازی سریع

بر اساس درکی که از افراز در مرتب سازی سریع داریم، اینک می‌توانیم الگوریتم آن را به صورت زیر بنویسیم:

• گام 1- مقدار بالاترین اندیس را به عنوان مقدار pivot انتخاب کن
• گام 2 – دو متغیر را برای اشاره به سمت چپ و راست لیست به جز pivot انتخاب کن.
• گام 3 – متغیر چپ به اندیس پایین اشاره می‌کند.
• گام 4- متغیر راست به اندیس بالا اشاره می‌کند.
• گام 5- مادمی که مقدار متغیر چپ کمتر از pivot باشد، به سمت راست حرکت کن.
• گام 6 – مادامی که متغیر راست بزرگ‌تر از pivot باشد، به سمت چپ حرکت کن.
• گام 7 – اگر هر دو وضعیتی که در گام‌های 5 و 6 اشاره کردیم مطابقت نداشتند، جای متغیرهای راست و چپ را تغییر بده
• گام 8 – اگر چپ > راست بود در این صورت جایی که این دو به هم می‌رسند، pivot جدید است.

شبه کد pivot مرتب سازی سریع

function partitionFunc(left, right, pivot)
   leftPointer = left
   rightPointer = right - 1

   while True do
      while A[++leftPointer] < pivot do //do-nothing end while while rightPointer > 0 && A[--rightPointer] > pivot do
         //do-nothing         
      end while
		
      if leftPointer >= rightPointer
         break
      else                
         swap leftPointer,rightPointer
      end if
		
   end while 
	
   swap leftPointer,right
   return leftPointer
	
end function

الگوریتم مرتب سازی سریع

با استفاده بازگشتی از الگوریتم pivot در نهایت به کوچک‌ترین اندازه ممکن برای افرازها می‌رسیم. سپس هر افراز برای مرتب سازی سریع مورد پردازش قرار می‌گیرد. الگوریتم بازگشتی برای مرتب سازی سریع به صورت زیر است:

• گام 1 - اندیسی که در انتهای سمت راست قرار دارد را pivot قرار بده
• گام 2 – آرایه را با استفاده از این مقدار pivot افراز کن
• گام 3 – بخش چپ افراز را با استفاده از مرتب سازی سریع به طور بازگشتی مرتب کن.
• گام 4 - بخش راست افراز را با استفاده از مرتب سازی سریع به طور بازگشتی مرتب کن.

شبه کد مرتب سازی سریع

procedure quickSort(left, right)

   if right-left <= 0
      return
   else     
      pivot = A[right]
      partition = partitionFunc(left, right, pivot)
      quickSort(left,partition-1)
      quickSort(partition+1,right)    
   end if		
   
end procedure

پیاده‌سازی الگوریتم مرتب سازی سریع در زبان C

#include 
#include 

#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
   int i;
	
   for(i = 0;i < count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i < MAX;i++) {
      printf("%d ",intArray[i]);
   }
	
   printf("]\n");
}

void swap(int num1, int num2) {
   int temp = intArray[num1];
   intArray[num1] = intArray[num2];
   intArray[num2] = temp;
}

int partition(int left, int right, int pivot) {
   int leftPointer = left -1;
   int rightPointer = right;

   while(true) {
      while(intArray[++leftPointer] < pivot) { //do nothing } while(rightPointer > 0 && intArray[--rightPointer] > pivot) {
         //do nothing
      }

      if(leftPointer >= rightPointer) {
         break;
      } else {
         printf(" item swapped :%d,%d\n", intArray[leftPointer],intArray[rightPointer]);
         swap(leftPointer,rightPointer);
      }
   }
	
   printf(" pivot swapped :%d,%d\n", intArray[leftPointer],intArray[right]);
   swap(leftPointer,right);
   printf("Updated Array: "); 
   display();
   return leftPointer;
}

void quickSort(int left, int right) {
   if(right-left <= 0) {
      return;   
   } else {
      int pivot = intArray[right];
      int partitionPoint = partition(left, right, pivot);
      quickSort(left,partitionPoint-1);
      quickSort(partitionPoint+1,right);
   }        
}

int main() {
   printf("Input Array: ");
   display();
   printline(50);
   quickSort(0,MAX-1);
   printf("Output Array: ");
   display();
   printline(50);
}

اگر کد فوق را کامپایل و اجرا کنیم، خروجی زیر حاصل می‌شود:

خروجی

Input Array: [4 6 3 2 1 9 7 ]
==================================================
 pivot swapped :9,7
Updated Array: [4 6 3 2 1 7 9 ]
 pivot swapped :4,1
Updated Array: [1 6 3 2 4 7 9 ]
 item swapped :6,2
 pivot swapped :6,4
Updated Array: [1 2 3 4 6 7 9 ]
 pivot swapped :3,3
Updated Array: [1 2 3 4 6 7 9 ]
Output Array: [1 2 3 4 6 7 9 ]
==================================================

در این نوشته تلاش کردیم تا الگوریتم‌های مرتب سازی عمده‌ای که ساختارهای داده‌ای مورد استفاده قرار می‌گیرند را با هم مرور کنیم. روش‌های دیگری هم مانند الگوریتم مرتب سازی شمارشی وجود دارند که البته به صورت رایج به عنوان «زیرروال» (Subroutine) تکنیک «مرتب‌سازی مبنایی» (Radix Sort) استفاده می‌شود.

در مورد هر روش مرتب سازی نیز هم الگوریتم و هم شبه کد مربوطه ارائه شد. همچنین پیاده‌سازی کامل آن در زبان C ارائه شده و توصیه می‌کنیم که این پیاده‌سازی را شخصاً کامپایل کرده و با بررسی بخش‌های مختلف آن به طور عملی با طرز کار هر یک از الگوریتم مرتب سازی آشنا شوید. توجه کنید که الگوریتم‌های مرتب سازی جزو مهم‌ترین الگوریتم‌های موجود در علوم رایانه هستند و هر نوع اپلیکیشنی که بخواهید بنویسید، می‌بایست از این الگوریتم‌ها در آن استفاده کنید. بنابراین یادگیری کامل این راهنما امری ضروری تلقی شود.