روش‌ های نمونه گیری (Sampling) در آمار — به زبان ساده

در روش‌های تحقیقات علمی، بررسی نمونه‌ای و تحقیقات آماری، «نمونه‌گیری» (Sampling) و روش های نمونه گیری به فرآیندی گفته می‌شود که براساس آن انتخاب اعضایی از جامعه آماری صورت می‌پذیرد. این کار با هدف برآورد پارامتر جامعه و یا شناخت بیشتر از آن انجام می‌شود.

اهمیت نمونه‌گیری را می‌توان صرفه‌جویی در زمان برای تهیه مشاهدات از جامعه آماری به منظور انجام تحقیق علمی دانست. معمولا نمونه‌گیری در مقابل سرشماری قرار دارد. سرشماری به منظور بررسی همه اعضای جامعه آماری به کار می‌رود ولی گاهی دسترسی به تمام اعضای این جامعه میسر نیست یا تعداد اعضای آن نامتناهی است.

هر «مشاهده» (Observation)، بیانگر مقدار یک یا چند ویژگی‌ (مانند وزن، قد و محل سکونت) از اعضای جامعه آماری است. انتخاب این‌گونه مشاهدات معمولا به روش‌های آماری وابستگی دارد.

برای آشنایی بیشتر با مفهوم جامعه آماری مطلب جامعه آماری — انواع داده و مقیاس‌های آن‌ها را مطالعه کنید. همچنین برای آگاهی از تعریف نمونه و کاربرد آن به مطلب نمونه‌گیری و بازنمونه‌گیری آماری (Sampling and Resampling) — به زبان ساده مراجعه کنید.

در این مطلب به بررسی روش های نمونه گیری تصادفی و غیرتصادفی پرداخته و شیوه‌های آن‌ها را بررسی می‌کنیم.

روش های نمونه گیری

انتخاب بعضی از اعضای جامعه آماری به منظور بررسی یا تحقیق علمی، روش نمونه‌گیری را تشکیل می‌دهد. روش‌های نمونه‌گیری در بسیاری از زمینه‌ها کاربرد دارند. برای مثال در صنایع، به منظور قبول یا رد یک محموله از محصولات از روش‌های نمونه‌گیری استفاده می‌شود. در پیش‌بینی نتیجه انتخابات نیز نمونه‌گیری کاربرد دارد.

فیلم آموزش کنترل کیفیت آماری – جامع و با نکات کاربردی در فرادرس

کلیک کنید

برای انتخاب نمونه از جامعه آماری ممکن است تهیه یک لیست از اعضای جامعه مناسب باشد. البته به شرطی که قادر به تهیه چنین لیستی باشیم. سپس با مشخص کردن تعداد مورد نیاز برای نمونه و انتخاب بعضی از این اعضا می‌توان نمونه را تهیه کرد.

روشی که برای انتخاب این اعضا به کار گرفته می‌شود،‌ نقش مهمی در تحلیل‌های و بررسی‌های آماری دارد. در این میان دو روش عمده برای نمونه‌‌گیری موجود است.

• نمونه‌گیری تصادفی: ممکن است انتخاب اعضا براساس احتمال و توزیع احتمال جامعه آماری صورت گیرد که این حالت را «نمونه‌گیری تصادفی» (Probability Sampling) می‌گویند.
• نمونه‌گیری غیرتصادفی: اگر شیوه نمونه‌گیری یا انتخاب اعضای نمونه براساس الگویی غیرتصادفی انجام شود،  آن را به نام «نمونه‌گیری غیرتصادفی» (Non-probability Sampling) می‌شناسند.

روش های نمونه گیری تصادفی

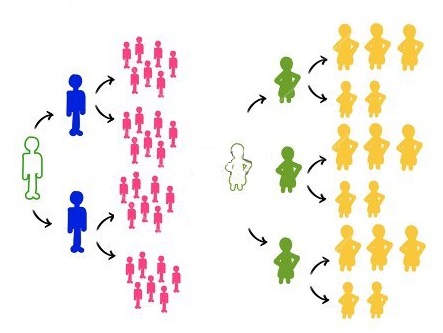
در این روش نمونه‌گیری، هر عضو از جمعیت‌ آماری دارای شانس مثبت برای انتخاب شدن در نمونه است. این کار کمک می‌کند که بتوان به نمونه‌ای دست پیدا کرد که بیانگر ویژگی‌های اکثر جامعه آماری باشد. برای مثال، فرض کنید، قرار است مجموع درآمد خانوار مربوط به خانواده‌هایی که در یک خیابان زندگی می‌کنند برآورد شود. به هر یک از خانه‌ها مراجعه و به طور تصادفی یکی از سرپرست‌های خانواده را انتخاب می‌کنیم.

انتخاب این فرد می‌تواند براساس نسبت دادن یک کد تصادفی به هر یک از سرپرست‌ها (پدر و مادر) انجام شود و سپس سرپرستی که دارای کد زوج است را برای تکمیل پرسش‌نامه انتخاب می‌کنیم.

کسی که تنها زندگی می‌کند به طور قطع انتخاب می‌شود ولی در خانواده‌‌ای که دارای ۲ سرپرست هستند احتمال انتخاب هر یک برابر با $$1/2$$ است. در نتیجه برآورد حاصل از نمونه با مقدار واقعی مجموع درآمد خانوار فاصله خواهد داشت. برای بهبود برآورد، درآمد سرپرست‌هایی که در جمع خانواده زندگی می‌کنند را دو برابر کرده و در جمع اثر می‌دهیم. این کار برآورد را به مقدار واقعی نزدیک‌تر می‌کند.

به طور معمول، نمونه‌گیری تصادفی می‌تواند به یکی از صورت‌های زیر انجام شود:

• نمونه‌گیری تصادفی ساده (Simple Random Sample)
• نمونه‌گیری سیستماتیک (Systematic Sampling)
• نمونه‌گیری طبقه‌ای (Stratified Sampling)
• نمونه‌گیری خوشه‌ای (Cluster Sampling)

نمونه گیری تصادفی ساده

در نمونه‌گیری تصادفی ساده، همه اعضای جامعه آماری شانسی برابر برای انتخاب شدن در نمونه را دارند. در این حالت جامعه آماری یکپارچه است و قابل تفکیک به بخش‌های مختلف نیست. این احتمال حتی برای هر زوج یا هر سه‌تایی و ... نیز وجود دارد.

این گونه نمونه‌گیری باعث کاهش اریبی و سادگی در نتایج حاصله می‌شود. به این معنی که واریانس یا پراکندگی بین اعضای نمونه می‌تواند برآوردگر خوبی برای واریانس جامعه باشد. به این ترتیب خطای نتایج از تحلیل آماری قابل محاسبه است.

در این شیوه نمونه‌گیری برای مثال، انتخاب ۱۰ نفر از یک جامعه، باعث می‌شود که به طور متوسط به اطلاعات ۵ مرد و ۵ زن دسترسی داشته باشیم. ولی اگر توزیع جامعه آماری از لحاظ نسبت زن و مرد نیز در انتخاب نمونه تصادفی دخیل باشد، بهتر می‌توان نمونه را انتخاب کرد و به نتایج حاصل از تحقیق اعتماد بیشتری داشت.

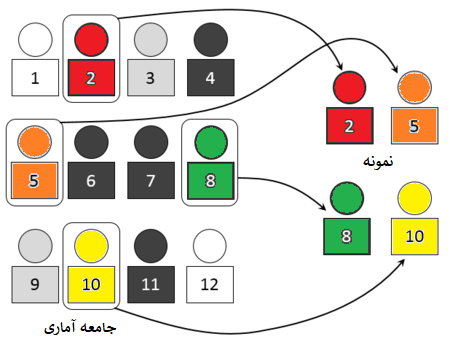
نمونه‌گیری تصادفی ساده، ممکن است هنگام جمع‌آوری اطلاعات از یک جمعیت هدف غیرمعمول بسیار ناقص عمل کند. در برخی موارد، محققان علاقه‌مند هستند که بررسی خاصی را روی زیر گروهی از جامعه آماری انجام دهند. برای مثال، محقق ممکن است بخواهد به بررسی عامل نژاد در توانایی عملکرد شغلی افراد مختلف بپردازد. استفاده از نمونه‌گیری تصادفی ساده در این حالت نمی‌تواند نیازهای محقق را برای تعیین نمونه مناسب برآورده کند.

نمونه‌ گیری سیستماتیک

اگر جامعه آماری را بتوان براساس یک ویژگی مرتب کرد، می‌توان از نمونه‌گیری سیستماتیک بهره گرفت. انتخاب اعضای نمونه در این شیوه، با استفاده از یک مقدار تصادفی و همچنین مقداری به عنوان فاصله اعضا صورت می‌گیرد.

فیلم آموزش فرآیند آماری در کنترل کیفیت آماری (رایگان) در فرادرس

کلیک کنید

برای انجام نمونه‌گیری سیستماتیک احتیاج به یک لیست مرتب شده از اعضای جامعه آماری داریم که دارای ستون ردیف است. ابتدا یک مقدار تصادفی کوچکتر از n انتخاب می‌شود. این مقدار نشان دهنده ردیفی است که اولین عضو نمونه در آن قرار دارد. سپس، شماره ردیف بعدی، توسط جمع شماره ردیف نمونه اول با مقدار فاصله محاسبه شده و عضو دوم نمونه بدست می‌آید. این کار تا رسیدن به تعداد نمونه مورد نظر ادامه پیدا می‌کند.

البته بعد از انتخاب عضوی از جامعه آماری در نمونه، شماره ردیف آن از لیست حذف شده و شماره‌ ردیف‌ها مجددا تولید می‌شوند. به همین علت اگر هنگام نمونه‌گیری به انتهای لیست برسیم، می‌توان از ابتدای لیست دوباره کار نمونه‌گیری را ادامه داد. به این ترتیب این شیوه نمونه‌گیری می‌تواند بدون جایگذاری تلقی شود.

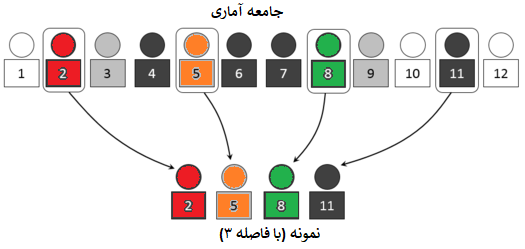
فرض کنید جدولی بر این اساس تشکیل شده که دارای شماره ردیف‌هایی از ۱ تا ۲۴ است و احتیاج داریم که یک نمونه ۸ تایی تهیه کنیم. اولین عضو نمونه به شیوه تصادفی از این لیست ۲۴ تایی انتخاب می‌شود. این کار ممکن است با انتخاب یک عدد تصادفی از بین ۱ تا ۲۴ صورت پذیرد. در این حالت فرض کنید که مشاهده دوم لیست انتخاب شده باشد.

انتخاب عضو دوم نمونه نیز با استفاده از پارامتر فاصله (k) صورت می‌گیرد. اگر به فرض مقدار k برابر با 5 باشد، عضوی از جامعه که دارای شماره ردیف 5+2=7 باشد، در نمونه قرار می‌گیرد.

عناصر بعدی نیز برهمین مبنا انتخاب می‌شوند. یعنی عنصر سوم نمونه دارای شماره ردیف 7+5=۱۲ خواهد بود. جدول زیر شماره ردیف‌های مربوط به اعضای جامعه آماری که باید در نمونه قرار گیرند را مشخص کرده است.

معمولا مقدار k‌ را به وسیله نسبت اندازه جامعه به اندازه نمونه محاسبه می‌کنند. در نتیجه داریم:

$$k=\frac{Population\;\; Size}{Sample\;\; Size}$$

نکته: گاهی برای راحتی کار، نمونه اول را از بین k عضو اول جامعه و بطور تصادفی انتخاب می‌کنند.

نمونه گیری طبقه ای

در حالتی که جامعه آماری دارای بخش‌های مجزایی باشد، می‌توان محدوده نمونه‌گیری را به بخش‌های مختلف تقسیم کرد. در این حالت هر بخش از جامعه به عنوان یک زیرجامعه تلقی شده که نسبت به بقیه بخش‌ها مستقل است. به این ترتیب با استفاده از نمونه‌گیری تصادفی از هر زیربخش به یک نمونه کامل خواهیم رسید. این روش را نمونه‌گیری طبقه‌ای می‌نامند.

این شیوه نمونه‌گیری دارای مزایای زیادی است که به بعضی از آن‌ها در زیر اشاره شده است:

• ایجاد بخش‌های مجزا از جامعه آماری، امکان بررسی گروه‌هایی از جامعه را به وجود می‌آورد که ممکن است در نمونه‌گیری تصادفی ساده در نظر گرفته نشوند.
• دقت محاسبات و برآوردهای حاصل از نمونه آماری را افزایش می‌دهد زیرا حجم نمونه از هر زیرگروه متناسب با حجم زیرجامعه‌ مربوط به خودش است.
• استفاده از شیوه نمونه‌گیری طبقه‌ای این امکان را می‌دهد که در هر زیربخش از جامعه آماری روش نمونه‌گیری خاصی به کار رود. بنابراین گاهی می‌توان به جای استفاده از نمونه‌گیری تصادفی در زیربخش‌ها از نمونه‌گیری خوشه‌ای نیز استفاده کرد.

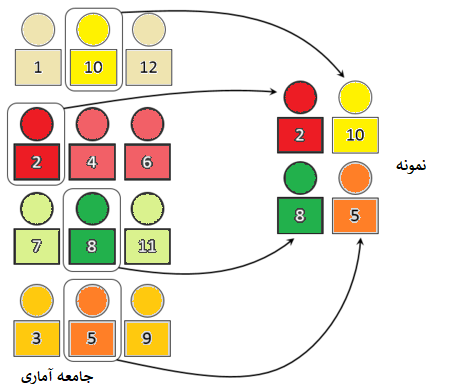
همچنین معیابی نیز برای این شیوه نمونه‌گیری می‌توان برشمرد:

• انتخاب ویژگی که براساس آن بتوان جامعه آماری را گروه‌بندی کرد، کار مشکلی و حساسی است.
• برای جامعه‌ای که به طور یکدست و همگن باشد، استفاده از چنین شیوه‌ای ممکن است، نتایج حاصل از تحقیق و تحلیل آماری را به گمراهی بکشد.
• هزینه و زمان در اجرای نمونه‌گیری طبقه‌ای نسبت به نمونه‌گیری تصادفی ساده نسبتا زیاد است.

البته تعیین بخش‌های مجزا از جامعه آماری در نمونه‌گیری طبقه‌ای، هزینه و زمان بیشتری نسبت به نمونه‌گیری تصادفی دارد. تعیین بخش‌های جامعه آماری باید به شکلی باشد که شرط‌های زیر برایش صدق کنند:

• پراکندگی در درون هر بخش کمینه باشد. به بیان دیگر حداکثر میزان شباهت را در هر بخش داشته باشیم.
• پراکندگی بین بخش‌ها بیشینه باشد. به بیان دیگر میزان شباهت بین بخش‌های جامعه آماری حداقل ممکن باشد.
• ویژگی که باعث ایجاد طبقات در جامعه آماری شده، بیشترین ارتباط یا وابستگی را با موضوع مورد تحقیق داشته باشد.

نمونه گیری خوشه ای

گاهی برای نمونه‌گیری از جامعه‌ای که اعضای آن در گروه‌هایی مجزا قرار دارند، از روش نمونه‌گیری خوشه‌ای استفاده می‌شود. این شیوه معمولا براساس بخش‌های مجزایی که توسط نواحی جغرافیایی تعیین می‌شوند به کار می‌رود. برای مثال اگر میزان درآمد خانوار مورد بحث باشد، نمونه‌گیری می‌تواند به صورت انتخاب ۱۰0۰ خانوار از شهرهای مختلف کشور صورت بگیرید. اگر از شیوه نمونه‌گیری تصادفی ساده استفاده کنیم باید از لیست خانوار که در مرکز آمار وجود دارد با استفاده از اعداد تصادفی یک نمونه به حجم ۱۰۰۰ انتخاب کنیم. این احتمال وجود دارد که بیشتر اعضای این نمونه به علت تراکم خانوار در استان تهران، محدود به این استان شوند و سهم استان‌های دیگر در برآورد مجموع درآمد خانوار کاهش یابد.

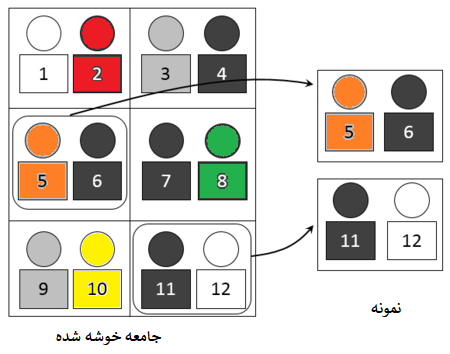
در نتیجه بهتر است برای بالا بردن دقت برآورد از شیوه نمونه‌گیری خوشه‌ای استفاده شود. برای چنین حالتی از بین استان‌های کشور به طور تصادف ۱۰ استان انتخاب می‌شود، از بین هر استان نیز ۱۰ شهر به طور تصادفی انتخاب شده و از هر شهر نیز ۱۰ خانه باز هم به طور تصادفی انتخاب می‌شود. در نتیجه یک نمونه ۱۰۰۰ تایی از خانوارها داریم که می‌توانیم پرسشنامه مربوط به درآمد را برایشان تکمیل کنیم.

این شیوه نمونه‌گیری در کسب اطلاعات کامل و با اهمیت از جامعه آماری با حفظ تغییر پذیری زیاد در اعضای نمونه کمک شایانی می‌کند. گاهی به نمونه‌گیری خوشه‌ای، روش «نمونه‌گیری چند سطحی» (Multistage Sampling) نیز گفته می‌شود. گام‌های این روش نمونه‌گیری به صورت زیر است:

• گام اول: تعیین خوشه‌ها برای تهیه نمونه‌ها
• گام دوم: انتخاب یک نمونه تصادفی از خوشه‌های مرحله اول
• گام سوم: انتخاب یک نمونه تصادفی از خوشه‌های مرحله دوم
• ....
• گام نهایی: انتخاب یک نمونه تصادفی از خوشه‌های مرحله قبلی

اگر در نمونه‌گیری خوشه‌ای یا چند سطحی فقط گام یک و دو طی شود، روش نمونه‌گیری، «یک مرحله‌ای» (One Stage) است و با طی شدن گام‌های ۱ تا ۳ به آن نمونه‌گیری دو مرحله‌ای (Two Stage) می‌گویند. در مثالی که در مورد نمونه‌گیری خوشه‌ای درآمد خانوار گفته شد، روش نمونه‌گیری سه مرحله‌ای است.

روش نمونه گیری غیرتصادفی

همانطور که اشاره شد، نمونه‌گیری، به کارگیری قسمتی از جامعه آماری به منظور شناسایی خصوصیات آن است. در نمونه‌گیری تصادفی، یا نمونه‌گیری برمبنای احتمال، هر عضو از جامعه آماری احتمال دارد که در نمونه آماری قرار گیرد و مشخصا این احتمال مثبت است. در مقابل در روش‌های نمونه‌گیری غیرتصادفی، این شرط وجود ندارد و ممکن است عضو یا اعضایی از جامعه آماری اصلا قابلیت قرارگیری در نمونه را نداشته باشند. شرط انتخاب اعضای نمونه آماری ممکن است براساس نظر شخصی یا قضاوت محقق صورت گیرد که در راستای هدف بررسی آماری است.

فیلم آموزش کنترل پیش بین مدل با متلب در فرادرس

کلیک کنید

معمولا بررسی‌ها و استنباط‌هایی که روی نمونه حاصل از روش نمونه‌گیری غیرتصادفی به دست آمده است، قابلیت انتقال به جامعه آماری را ندارد. به همین دلیل نتایجی که از طریق روش های نمونه گیری غیرتصادفی بدست می‌آید ممکن است با نتایج حاصل از نمونه‌گیری تصادفی متفاوت باشد. بنابراین روش نمونه‌گیری غیرتصادفی در زمینه‌هایی به کار گرفته می‌شود که محقق سعی در ایجاد یک نظریه برای بخشی از جامعه آماری دارد و فقط با تکرار عمل نمونه‌گیری غیرتصادفی می‌توان به نظریه‌ای برمبنای نتایج علمی حاصله دست یافت.

روش های نمونه گیری غیرتصادفی معمولا به منظور تایید تئوری‌هایی که از قبل وجود دارند بخصوص برای تحلیل داده‌های کیفی به کار گرفته می‌شود تا محقق بتواند به توصیف یک پدیده در بخشی از جامعه آماری بپردازد. یکی از جنبه‌های موثر در به کارگیری روش‌های نمونه‌گیری غیرتصادفی، هزینه کم‌تر و زمان کوتاه‌تر برای حصول به نمونه مورد نظر در مقابل با روش‌های نمونه‌گیری تصادفی است. در این میان می‌توان به روش‌های نمونه‌گیری غیرتصادفی مانند روش «نمونه‌گیری گلوله برفی» (Snowball Sampling)، «نمونه‌گیری اتفاقی» (Accidental Sampling)، «نمونه‌گیری متوالی» (Consecutive Sampling) و «نمونه‌گیری قضاوتی» (Judgmental Sampling) اشاره کرد.

نمونه گیری گلوله برفی

در این روش اولین عضو نمونه، به طریقی انتخاب می‌شود که بیشترین ارتباط را با موضوع مورد تحقیق دارد. از طریق ارتباط این عضو با اعضای دیگر جامعه آماری، امکان دسترسی به سایر نمونه‌ها میسر می‌شود. به این ترتیب اعضای نمونه حاصل شده، مانند یک شبکه اجتماعی به یکدیگر پیوند داشته و می‌توانند بیشترین اطلاعات را در مورد موضوع تحقیق و شناخت پدیده مورد نظر در اختیار محقق قرار دهند. در این حالت نمونه حاصل دارای اریبی خواهد بود و اعضایی از جامعه که در یک گروه خاص هستند شانس بیشتری برای عضویت در نمونه را دارند.

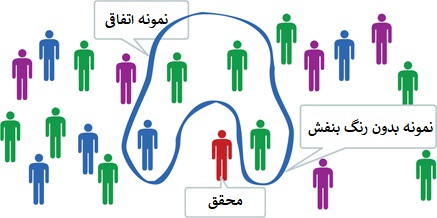
نمونه گیری اتفاقی

اعضای جامعه آماری با توجه به قابل دسترس بودن در نمونه جای می‌گیرند. برای مثال نمونه می‌تواند از دوستان،‌ همکاران و یا فروشندگان یک مرکز خرید تشکیل شود. در این روش باز هم نمونه حاصل دارای اریبی است زیرا نتایج حاصل از تحقیق به گروه خاصی از جامعه آماری وابسته است.

نمونه گیری متوالی

اگر نمونه‌گیری را به صورتی انجام دهیم که با استفاده از یک یا چند شرط اعضای جامعه را محدود کرده و سپس آن را اجرایی کنیم، در اصل روش نمونه‌گیری متوالی را به کار بسته‌ایم. عمل انتخاب اعضای نمونه تا رسیدن به حجم نمونه مورد نیاز ادامه پیدا می‌کند. برای مثال اگر منظور از نمونه‌گیری بررسی تعداد خودروهای قرمز رنگ باشد، می‌توان نمونه را به یک چهار راه محدود و رنگ خودرو ها را یادداشت کرد. نسبت تعداد خودروهای قرمز رنگ به کل می‌تواند درصد خودروهای قرمز رنگ را تخمین بزند.

نمونه گیری قضاوتی

در این روش، محقق براساس نظر و پیشینه‌ای که در مورد اعضای جامعه آماری دارد، دست به نمونه‌گیری می‌زند. انتخاب یا عدم انتخاب عضوی از جامعه در نمونه بسته به نظر محقق و تجربیات او دارد. معمولا این روش در جوامع آماری محدود و با حجم کم به کار می‌رود زیرا محقق باید در مورد تک تک اعضا اطلاعات قبلی داشته باشد تا بتواند نمونه حاصل را بهتر انتخاب کند.

هر چند که روش های نمونه گیری تصادفی و غیر تصادفی دو روش جداگانه محسوب می‌شوند ولی در برخی از روش‌های تحقیق ممکن است ترکیبی از هر دو روش برای تهیه نمونه به کار گرفته شود. با این کار نتایج حاصل از نمونه‌ها، قابلیت بیشتری دارند تا به جامعه آماری تعمیم داده شوند، هرچند ترکیب این دو روش ممکن است باعث صرف زمان و هزینه بیشتری شود.