فرادرسمقیاسبندی قضیه فیثاغورس — ریاضیات به زبان ساده
قضیه فیثاغورس را نه تنها در مورد مثلث بلکه در مورد هر شکلی می‌توان به کار گرفت. با استفاده از قضیه فیثاغورس می‌توان تقریباً هر نوع مسافتی را اندازه‌گیری کرد. این فرمول 2000 ساله همچنان ترفندهای زیادی دارد که به ما نشان دهد. اگر فرمول فیثاغورس را از شکل زیر:
$$c=\sqrt{a^2 + b^2}$$
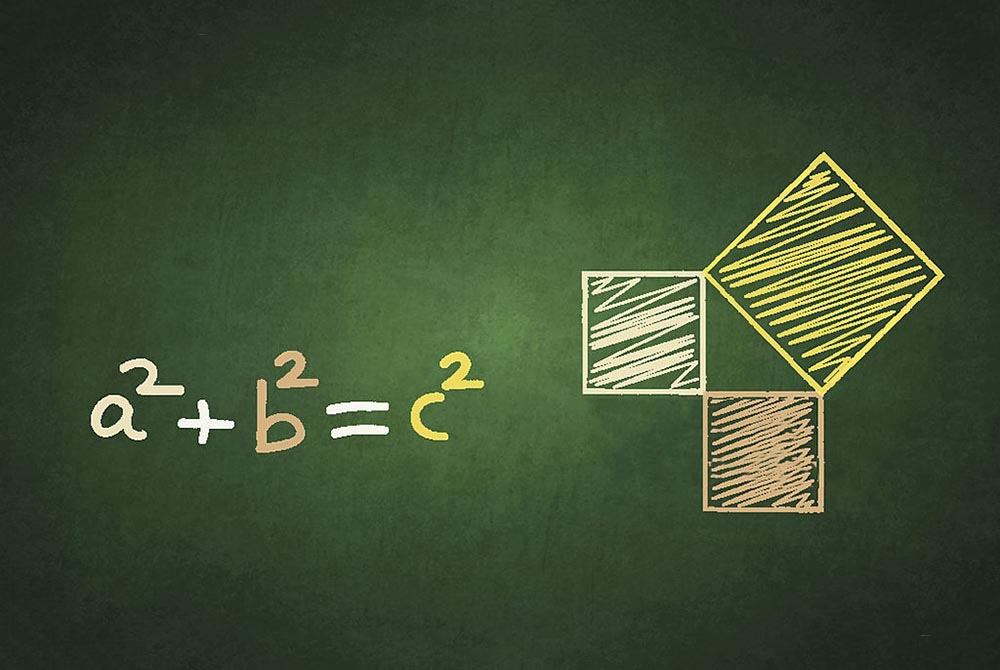
به صورت زیر بازنویسی کنیم:
$$c=a.\sqrt{(1 + (b/a)^2)}$$
می‌توانیم درک بهتری از رابطه بین شیب و مسافت به دست آوریم. در ادامه این مسئله را بیشتر توضیح می‌دهیم.
تغییر مقیاس مثلث
تغییر مقیاس باعث می‌شود بینش‌های جدیدی کسب کنیم. با این که می‌دانیم درآمد 500 میلیون در سال درآمد بالایی است؛ اما وقتی تصور کنیم همه چیز 10 برابر ارزان‌تر است شاید تصور چنین درآمدی ملموس‌تر باشد. مثلاً تصور کنید یک خودرو یا لپ‌تاپ 10 برابر ارزان‌تر از قیمت کنونی آن باشد.
فرمول‌های تغییر مقیاس می‌توانند راهگشا نیز باشند. ابتدا با مثلث مشهور به اضلاع 5-4-3 آغاز می‌کنیم و هر یک از اضلاع آن را به 3 قسمت تقسیم می‌کنیم:
اینک مثلث قرمز کوچک‌تر را با اضلاع 1=3/3، 3/4 و 3/5 داریم. در واقع این نسخه کوچک شده‌ای از مثلث بزرگ‌تر است و قضیه فیثاغورس همچنان صدق می‌کند:
$$1^2 + (4/3)^2 = (5/3)^2$$
بنابراین باید پرسید چرا این مثلث ویژه است؟ با این که این تغییر مقیاس، کار چندان عجیبی به نظر نمی‌رسد، اما نتایج شگفت‌انگیزی دارد.
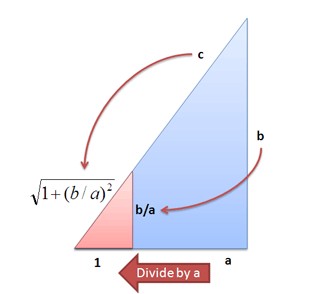
ابتدا باید گفت که می‌توان هر نوع مثلثی را به مثلثی تبدیل کرد که کوچک‌ترین ضلعش به اندازه 1 باشد. همه مثلث‌های مشابه یعنی مثلث‌هایی با نسبت اضلاع 3-4-5 یا 6-8-10 را می‌توان به این مثلث کوچک تبدیل کرد.
این مثلث کوچک خصوصیات جالبی دارد. در این مثلث تنها نسبت b/a مهم است. تنها عدد معنی‌دار 1 و b/a هستند:
وتر مثلث کوچک = $$\sqrt{1 + (b/a)^2}$$
اما این b/a چه خصوصیت ویژه‌ای دارد؟ این همان شیب خط وتر است. آن را شیب، گرادیان، مشتق و بسیاری نام‌های دیگر می‌نامند؛ اما در هر حال b/a نشان دهنده تغییرات وتر است.
بدین ترتیب برای هر واحدی که روی ضلع کوچک مثلث طی کنیم، روی ضلع دیگر شیبی به اندازه b/a به دست می‌آوریم. در یک مثلث 3-4-5، اگر 1 واحد به سمت شرق حرکت کنیم، 4/3 واحد به سمت شمال حرکت کرده‌ایم. و طول وتر نیز 5/3 یا 1.66 برای هر 1 واحد حرکت به سمت شرق افزایش می‌یابد
می‌بینیم که نتیجه مقیاس‌بندی جالب است. ما از شیب وتر (b/a) برای یافتن مسافت پیموده شده برای هر واحد حرکت شرقی به صورت $$c = \sqrt{(5^2+12^2)} \ = 13$$ استفاده می‌کنیم.
بررسی یک مثال
شاید نتیجه‌گیری فوق در ابتدا کمی غریب به نظر بیاید، لذا مثالی را بررسی می‌کنیم. فرض کنید از نقطه‌ای شروع به حرکت کرده و 5 واحد به سمت شرق و 12 واحد به سمت شمال می‌رویم. فاصله ما اینک از نقطه مبدأ حرکت چه مقدار است؟
رویکرد سنتی با بهره‌گیری از قضیه فیثاغورس به صورت زیر است:
$$c = \sqrt{(5^2+12^2)} \ = 13$$
این پاسخ صحیح است؛ اما با استفاده از روش مثلث کوچک محاسبه به صورت زیر خواهد بود:
در شکل فوق به جای مثلث بزرگ، آن را تغییر مقیاس داده‌ایم و یک مثلث کوچک با اضلاع 1=5/5 و 12/5 داریم. اینک وتر کوچک برابر با $$\sqrt{1 + (12/5)^2} = 2.6$$ است. این بدان معنی است که 2.6 واحد حرکت در راستای وتر به ازای هر واحد حرکت شرقی صورت می‌پذیرد. حال اگر بخواهیم مسافت را برای 5 واحد شرقی محاسبه کنیم مقدار به دست آمده به صورت 13 = 2.6 × 5 واحد خواهد بود، که همان نتیجه قبلی است.
اما حُسن این روش آن است که دیگر نیازی به مجذور گیری نیست و با توجه به این که نسبت اضلاع یکسان است. برای هر مسافتی که بخواهیم محاسبه کنیم کافی است در شیب وتر (در اینجا 2.6) آن را ضرب کنیم.
بدین ترتیب مسافت پیموده شده را یک ضرب معمولی نیز می‌توان یافت. این رویکرد هم برای انسان و هم برای رایانه سریع‌تر است. شاید اگر با روش‌های عجیب و غریبی که برنامه‌نویسان برای احتراز از محاسبه مجذور در برنامه‌های رایانه‌ای استفاده می‌کنند آشنا بودید، بیشتر به فایده این رویکرد پی می‌بردید.
فرمول‌های استاتیک و دینامیک
می‌دانیم که قضیه فیثاغورس روی متغیرهای a و b به صورت مستقل از هم تمرکز دارد:
$$c=\sqrt{a^2 + b^2}$$
ما a و b را عناصری جدا از هم می‌دانیم که باید به توان 2 رسیده و با هم جمع شوند. این رویکرد سرراست است و هنگام طراحی پل‌ها یا خلق تصاویری از مثلث‌ها کاملاً مفید محسوب می‌شود. چون فرمول سنتی روی مقادیر نهایی تمرکز دارد. اما نسخه تغییر مقیاس یافته شکل جدیدی دارد:
$$c=a.\sqrt{(1 + (b/a)^2)}$$
در این جا ما دیگر به آن دو کمیت مجزا علاقه زیادی نداریم و صرفاً نسبت آن‌ها b/a که شیب وتر است برای ما حائز اهمیت تلقی می‌شود. این شیب یک ثابت مقیاس‌بندی به صورت $$\sqrt{(1 + (b/a)^2)}$$ ایجاد می‌کند که حرکت رو به شرق ما را به مسافت طی شده تبدیل می‌کند. فرمول دینامیک روی نسبت‌های تغییر تمرکز دارد.
اگر یک تابع فرضی (f(x داشته باشیم می‌توانیم قضیه فیثاغورس دینامیک خود را به صورت زیر بنویسیم:
مسافت در راستای مسیر = $$x.\sqrt{1 + (slope)^2}$$
این مفهوم در حسابان برای یافتن طول هر خط مستقیم یا منحنی استفاده می‌شود؛ اما این موضوع نوشته دیگری است.
نکته کلیدی این است که یک فرمول منفرد را می‌توان به شیوه متفاوتی درک کرد و بدین ترتیب بینش‌های جدیدی به دست آورد. بنابراین سعی کنید همیشه کنجکاوی خود را حفظ کنید چون وقتی فکر کنیم همه چیز را یافته‌ایم، دیگر چیز جدیدی یاد نخواهیم گرفت.
نکته نهایی: شیب در برابر مسافت
نکته‌ای که شاید در این نوشته موجب سردرگمی می‌شود، ایده شیب (b/a) از روی مسافت پیموده شده (وتر، c) باشد.
شیب برابر با b/a به میزان ارتفاع گرفتن از سطح افق گفته می‌شود. یعنی وقتی مسافتی پیموده می‌شود چه مقدار ارتفاع افزایش می‌یابد. برای نمونه می‌گوییم شیب تپه چقدر است. متأسفانه کلمه شیب باعث می‌شود یاد دامنه تپه بیفتیم؛ اما شیب واقعاً به ارتفاع مربوط است.
مسافت (وتر) اشاره به دامنه تپه دارد، یعنی چه مقدار حرکت کرده‌اید. در اینجا میزان تند بودن شیب اهمیتی ندارد، چون شما متری را روی زمین می‌گذارید و مسافت را اندازه‌گیری می‌کنید. این مسافت می‌تواند مسطح، عمودی یا از بالا به پایین باشد. آیا طول یک نان سنگک ربطی به جهتی که آن را گرفته‌اید دارد؟
اما در دنیای روزمره ما شیب و مسافت با هم مرتبط هستند، چون ما در اغلب موارد موقعیت‌های مختلف را بر حسب واحد شرقی (مختصات x) بیان می‌کنیم و نه واحدهای مسافت. بنابراین وقتی یک نقشه می‌بینید نوشته است «یک کیلومتر به سمت شرق برو» و شما روبروی یک کوه (شیب بلند) قرار دارید، در واقع شما باید مسافتی بیش از یک کیلومتر حرکت کنید. زمانی که روی زمین مسطح با شیب صفر حرکت می‌کنیم، 1 کیلومتر به سمت شرق صرفاً 1 کیلومتر است و نه بیشتر یا کمتر. هر چه شیب بیشتر باشد، مسافتی که باید برای حرکت 1 کیلومتری به سمت شرق حرکت کنید بیشتر خواهد شد.
در این مورد هم می‌بینیم که قضیه فیثاغورس ربطی به مثلث‌ها ندارد و برای تبدیل شیب به مسافت پیموده شده استفاده می‌شود.
==
