رویه های بازگشتی (Recursive Procedures) — ساختار داده و الگوریتم ها

برخی زبان‌های برنامه‌نویسی این امکان را فراهم ساخته‌اند که یک ماژول یا تابع خود را فراخوانی کند. این وضعیت «بازگشت» نامیده می‌شود. در بازگشت، یک تابع مثلاً آلفا یا خودش را مستقیماً فراخوانی می‌کند و یا تابع بتا را فراخوانی می‌کند که آن تابع، آلفا را بازخوانی می‌کند. بدین ترتیب تابع آلفا به صورت بازگشتی فراخوانی می‌شود.

مثال – فراخوانی یک تابع از سوی خود

int function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

مثال – تابعی یک تابع دیگر را فراخوانی می‌کند که این تابع دوم، تابع اولیه را فراخوانی می‌کند.

iint function(int value) {
   if(value < 1)
      return;
   function(value - 1);

   printf("%d ",value);   
}

مشخصات

یک تابع بازگشتی همانند حلقه می‌تواند وارد حالت نامتناهی شود. برای جلوگیری از اجرای نامتناهی توابع بازگشتی، دو خصوصیت هستند که باید رعایت شوند:

• معیار مبنا - دست‌کم باید یک معیار یا شرط مبنا وجود داشته باشد به طوری که وقتی شرط برقرار شد، تابع متوقف شود و دیگر خود را فراخوانی نکند.
• رویکرد پیش‌رونده – فراخوانی‌های بازگشتی باید به نحوی پیش روند که هر بار با فراخوانی بازگشتی، تابع به شرط مبنا نزدیک‌تر شود.

پیاده‌سازی

بسیاری از زبان‌های برنامه‌نویسی، بازگشت را به وسیله پشته‌ها (stacks) پیاده‌سازی می‌کنند. به طور کلی هر زمان که یک تابع (Caller) تابع دیگر (Callee) یا خودش را به عنوان Callee فراخوانی می‌کند، تابع فراخواننده کنترل اجرایی را به تابع فراخوانی شده انتقال می‌دهد. این فرایند انتقال می‌تواند شامل انتقال بخشی از داده‌ها از فراخواننده به فراخوانی شده نیز باشد.

فیلم آموزش ساختمان داده ها در فرادرس

کلیک کنید

این بدان معنی است که تابع فراخواننده باید به طور موقت اجرای خود را معلق کند و بعدتر زمانی که کنترل اجرایی را مجدداً از تابع فراخوانی شده دریافت کرد، عملکرد خود را از سر گیرد. در این زمان، تابع فراخواننده باید دقیقاً از همان نقطه‌ای کار خود را آغاز کند که متوقف شده بود. همچنین باید دقیقاً همان مقادیر داده‌ای که مشغول کار روی آن بود را ذخیره کند. به این منظور، رکورد فعال‌سازی (یا قاب پشته) برای تابع فراخواننده ایجاد می‌شود.

این رکورد فعال‌سازی شامل اطلاعاتی است که به متغیرهای محلی، پارامترهای شکلی، آدرس بازگشت و همه اطلاعاتی که به تابع فراخوانی شده ارسال کرده است، مربوط می‌شوند.

تحلیل بازگشت

ممکن است فکر کنید که اصولاً چه لزومی به استفاده از بازگشت وجود دارد، چون همان کار را می‌توان با استفاده از چرخه (تکرار) نیز انجام داد. اولین دلیل برای استفاده از بازگشت این است که باعث می‌شود برنامه خوانایی بیشتری داشته باشد. دلیل دیگر این است که به دلیل بهینه‌سازی‌های جدیدی که روی سی‌پی‌یوها اعمال شده است، استفاده از رویه‌های بازگشتی به جای چرخه‌ها، بسیار کارآمدتر است.

فیلم آموزش روابط بازگشتی در ریاضیات گسسته (رایگان) در فرادرس

کلیک کنید

پیچیدگی زمانی

در مورد چرخه‌ها از تعداد تکرار برای محاسبه پیچیدگی زمانی استفاده می‌کنیم. به طور مشابه در مورد بازگشت نیز فرض می‌کنیم که همه چیز ثابت است و سعی می‌کنیم تعداد دفعاتی که فراخوانی بازگشتی صورت می‌گیرد را محاسبه کنیم. یک فراخوانی که به یک تابع صورت می‌گیرد دارای پیچیدگی (O(1 است و از این رو اگر n بار فراخوانی بازگشتی صورت بگیرد، پیچیدگی زمانی برابر با (O(n خواهد بود.

پیچیدگی فضایی

پیچیدگی فضایی به معنی مقدار فضایی است که برای اجرای یک ماژول مورد نیاز است. در مورد چرخه‌ها، کامپایلر به ندرت به فضای بیشتری نیاز خواهد داشت. کامپایلر به طور مداوم مقادیر متغیرهای مورد استفاده از سوی چرخه را به‌روزرسانی می‌کند. اما در مورد بازگشت، سیستم باید رکوردهای فعال‌سازی را هر بار که فراخوانی بازگشتی صورت می‌گیرد، به‌روزرسانی کند. از این رو پیچیدگی فضایی تابع‌های بازگشتی ممکن است بالاتر از تابع‌های دارای چرخه باشد. در ادامه برج هانوی (Hanoi) را به عنوان یکی از مثال‌های کلاسیک استفاده از توابع بازگشتی بررسی می‌کنیم.

برج هانوی

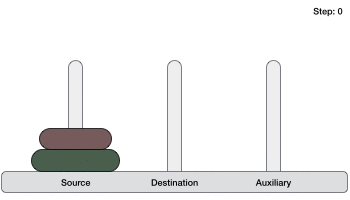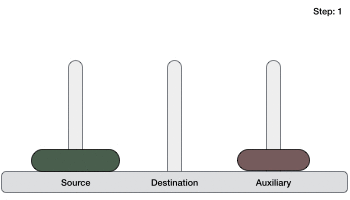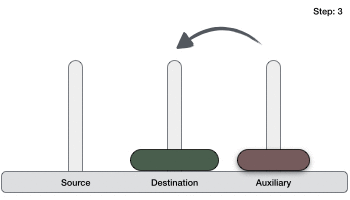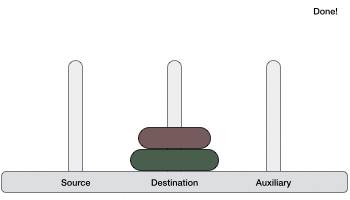
برج هانوی یک مسئله ریاضیاتی است که شامل سه برج است و همان طور که در تصویر زیر مشخص است، بیش از یک حلقه وجود دارد.

سه حلقه با اندازه‌های مختلف با ترتیب صعودی روی هم قرار می‌گیرند، یعنی حلقه کوچک‌تر در بالا قرار گرفته و حلقه‌های بزرگ‌تر به ترتیب زیر آن هستند. نسخه‌های دیگری از این مسئله نیز وجود دارند که در آن تعداد حلقه‌ها بیشتر است؛ اما تعداد برج‌ها همواره ثابت است.

قواعد

هدف از این مسئله آن است که همه حلقه‌ها بدون نقض توالی چیدمان‌ها که در بخش قبل توضیح دادیم به برج بعدی انتقال یابند. چند قاعده در این فرایند وجود دارند که باید رعایت شوند:

• در هر زمان تنها یک حلقه بین برج‌ها می‌تواند انتقال یابد.
• تنها حلقه فوقانی را می‌توان جابجا کرد.
• حلقه‌های بزرگ‌تر نمی‌توانند روی حلقه‌های کوچک‌تر از خود قرار گیرند.

برج هانوی‌ای که دارای n حلقه باشد را در کمترین حالت می‌توان در 2ⁿ−1 مرحله حل کرد. در تصویر فوق مشخص است که مسئله‌ای با 3 حلقه را می‌توان در 7 = 1 - 2³  مرحله حل کرد.

الگوریتم

برای نوشتن الگوریتمی برای برج‌ هانوی، ابتدا باید بدانیم که چگونه می‌توانیم مسئله را با تعداد اندکی از حلقه‌ها برای مثال یک یا دو عدد، حل کنیم. میله‌ها را به صورت مبدأ، مقصد و کمکی نام‌گذاری می‌کنیم (از میله کمکی صرفاً برای کمک به جابجایی حلقه‌ها استفاده می‌شود.) اگر تنها یک حلقه داشته باشیم، می‌توانیم به سادگی آن را از میله مبدأ به میله مقصد انتقال دهیم.

اگر دو حلقه داشته باشیم:

• ابتدا حلقه کوچک‌تر (فوقانی) را به میله کمکی انتقال می‌دهیم.
• سپس حلقه بزرگ‌تر (زیرین) را به میله مقصد انتقال می‌دهیم.
• در نهایت حلقه کوچک‌تر را از میله کمکی به میله مقصد انتقال می‌دهیم.

بنابراین اینک می‌توانیم الگوریتمی برای برج هانوی با بیش از دو حلقه طراحی کنیم. ما پشته حلقه‌ها را به دو بخش تقسیم می‌کنیم. بزرگ‌ترین حلقه (حلقه n-اُم) را در یک طرف و باقی حلقه‌ها (n-1 عدد) را در طرف دیگر قرار می‌دهیم.

هدف نهایی ما این است که دیسک n را از مبدأ به مقصد انتقال دهیم و سپس همه n-1 حلقه دیگر را روی آن قرار دهیم. می‌توانیم تصور کنیم که می‌توانیم از همان روش بازگشتی برای همه مجموعه حلقه‌ها استفاده کنیم. مراحل کار به صورت زیر است:

• گام 1 – n-1 حلقه را از مبدأ به میله کمکی انتقال دهید.
• گام 2 – حلقه n-ام را از مبدأ به مقصد انتقال دهید.
• گام 3 – n-1 حلقه را از میله کمکی به حلقه مقصد انتقال دهید.

الگوریتم بازگشتی برای برج هانوی به صورت زیر خواهد بود:

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

در ادامه الگوریتم فوق را در زبان C پیاده‌سازی کرده‌ایم.

پیاده‌سازی زبان C

#include 
#include 

#define MAX 10

int list[MAX] = {1,8,4,6,0,3,5,2,7,9};

void display(){
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0; i < MAX; i++) {
      printf("%d ",list[i]);
   }
	
   printf("]\n");
}

void bubbleSort() {
   int temp;
   int i,j;
   bool swapped = false;       
   
   // loop through all numbers 
   for(i = 0; i < MAX-1; i++) { 
      swapped = false;
		
      // loop through numbers falling ahead 
      for(j = 0; j < MAX-1-i; j++) { printf("Items compared: [ %d, %d ] ", list[j],list[j+1]); // check if next number is lesser than current no // swap the numbers. // (Bubble up the highest number) if(list[j] > list[j+1]) {
            temp = list[j];
            list[j] = list[j+1];
            list[j+1] = temp;

            swapped = true;
            printf(" => swapped [%d, %d]\n",list[j],list[j+1]);
         } else {
            printf(" => not swapped\n");
         }
      }

      // if no number was swapped that means 
      //   array is sorted now, break the loop. 
      if(!swapped) {
         break;
      }
      
      printf("Iteration %d#: ",(i+1)); 
      display();                     
   }    
}

int main() {
   printf("Input Array: ");
   display();
   printf("\n");
   bubbleSort();
   printf("\nOutput Array: ");
   display();
}

اگر کد فوق را کامپایل کرده و اجرا کنید، خروجی زیر را مشاهده می‌کنید.

خروجی

Input Array: [1 8 4 6 0 3 5 2 7 9 ]

     Items compared: [ 1, 8 ]  => not swapped
     Items compared: [ 8, 4 ]  => swapped [4, 8]
     Items compared: [ 8, 6 ]  => swapped [6, 8]
     Items compared: [ 8, 0 ]  => swapped [0, 8]
     Items compared: [ 8, 3 ]  => swapped [3, 8]
     Items compared: [ 8, 5 ]  => swapped [5, 8]
     Items compared: [ 8, 2 ]  => swapped [2, 8]
     Items compared: [ 8, 7 ]  => swapped [7, 8]
     Items compared: [ 8, 9 ]  => not swapped
Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ]
     Items compared: [ 1, 4 ]  => not swapped
     Items compared: [ 4, 6 ]  => not swapped
     Items compared: [ 6, 0 ]  => swapped [0, 6]
     Items compared: [ 6, 3 ]  => swapped [3, 6]
     Items compared: [ 6, 5 ]  => swapped [5, 6]
     Items compared: [ 6, 2 ]  => swapped [2, 6]
     Items compared: [ 6, 7 ]  => not swapped
     Items compared: [ 7, 8 ]  => not swapped
Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ]
     Items compared: [ 1, 4 ]  => not swapped
     Items compared: [ 4, 0 ]  => swapped [0, 4]
     Items compared: [ 4, 3 ]  => swapped [3, 4]
     Items compared: [ 4, 5 ]  => not swapped
     Items compared: [ 5, 2 ]  => swapped [2, 5]
     Items compared: [ 5, 6 ]  => not swapped
     Items compared: [ 6, 7 ]  => not swapped
Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ]
     Items compared: [ 1, 0 ]  => swapped [0, 1]
     Items compared: [ 1, 3 ]  => not swapped
     Items compared: [ 3, 4 ]  => not swapped
     Items compared: [ 4, 2 ]  => swapped [2, 4]
     Items compared: [ 4, 5 ]  => not swapped
     Items compared: [ 5, 6 ]  => not swapped
Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ]
     Items compared: [ 0, 1 ]  => not swapped
     Items compared: [ 1, 3 ]  => not swapped
     Items compared: [ 3, 2 ]  => swapped [2, 3]
     Items compared: [ 3, 4 ]  => not swapped
     Items compared: [ 4, 5 ]  => not swapped
Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ]
     Items compared: [ 0, 1 ]  => not swapped
     Items compared: [ 1, 2 ]  => not swapped
     Items compared: [ 2, 3 ]  => not swapped
     Items compared: [ 3, 4 ]  => not swapped

Output Array: [0 1 2 3 4 5 6 7 8 9 ]

یکی دیگر از مثال‌های کلاسیک برای بررسی رویه‌های بازگشتی، سری فیبوناچی است که در ادامه آن را نیز بررسی می‌کنیم.

سری فیبوناچی

در سری فیبوناچی با افزودن دو عدد قبلی، عدد بعدی ایجاد می‌شود. سری فیبوناچی از دو عدد آغاز می‌شود که آن‌ها را F0 و F1 می‌نامیم. مقادیر اولیه F0 و F1 را می‌توان به ترتیب 0,1 و یا 1,1 در نظر گرفت.

فیلم مجموعه آموزش ساختمان داده و طراحی الگوریتم – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

سری فیبوناچی شرایط زیر را دارد:

Fn = Fn-1 + Fn-2

از این رو سری فیبوناچی مانند زیر خواهد بود:

F8 = 0 1 1 2 3 5 8 13

یا

F8 = 1 1 2 3 5 8 13 21

به منظور نمایش بهتر این سری، در ادامه آن را به صورت تصویر متحرکی ارائه کرده‌ایم:

الگوریتم تکرار فیبوناچی

ابتدا تلاش می‌کنیم پیش‌نویسی از الگوریتم تکرار برای سری‌های فیبوناچی تهیه کنیم:

Procedure Fibonacci(n)
Procedure Fibonacci(n)
   declare f0, f1, fib, loop 
   
   set f0 to 0
   set f1 to 1
   
   display f0, f1
   
   for loop ← 1 to n
   
      fib ← f0 + f1   
      f0 ← f1
      f1 ← fib

      display fib
   end for
	
end procedure

پیاده‌سازی الگوریتم فوق در زبان C به صورت زیر است:

پیاده‌سازی زبان C

#include 

int factorial(int n) {
   //base case
   if(n == 0) {
      return 1;
   } else {
      return n * factorial(n-1);
   }
}

int fibbonacci(int n) {
   if(n == 0){
      return 0;
   } else if(n == 1) {
      return 1;
   } else {
      return (fibbonacci(n-1) + fibbonacci(n-2));
   }
}

int main() {
   int n = 5;
   int i;
	
   printf("Factorial of %d: %d\n" , n , factorial(n));
   printf("Fibbonacci of %d: " , n);
	
   for(i = 0;i<n;i++) {
      printf("%d ",fibbonacci(i));            
   }
}

اگر کد فوق را کامپایل و اجرا کنیم، خروجی زیر به دست می‌آید:

خروجی

Factorial of 5: 120

Fibbonacci of 5: 0 1 1 2 3

الگوریتم بازگشتی سری فیبوناچی

در ادامه الگوریتم سری فیبوناچی را به صورت بازگشتی تعریف کرده‌ایم:

#include <stdio.h>
START
Procedure Fibonacci(n)
   declare f0, f1, fib, loop 
   
   set f0 to 0
   set f1 to 1
   
   display f0, f1
   
   for loop ← 1 to n
   
      fib ← f0 + f1   
      f0 ← f1
      f1 ← fib

      display fib
   end for

END

اگر این الگوریتم را نیز در زبان C پیاده سازی کنیم خروجی برنامه شبیه وضعیت قبل خواهد بود:

خروجی

Factorial of 5: 120

Fibbonacci of 5: 0 1 1 2 3

اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد می‌کنیم موارد زیر را نیز ملاحظه کنید:

• آموزش روش های حل روابط بازگشتی
• آموزش تجزیه بازگشتی پیشگو در طراحی کامپایلر
• مجموعه آموزش‌های مهندسی نرم افزار
• آموزش رابطه های بازگشتی در طراحی الگوریتم و ساختمان گسسته (مرور – تست کنکور ارشد)
• روش پسگام – مبانی و مفاهیم
• الگوریتم ژنتیک و محاسبات تکاملی

==