اعداد تصادفی (Random Numbers) — تاریخچه و کاربردها

ضرورت استفاده از «اعداد تصادفی» (Random Number) در صنعت، نمونه‌گیری و توزیع‌های آماری و بخصوص «رمزنگاری» (Cryptography) اطلاعات رایانه‌ای برهیچ کس پوشیده نیست. ولی سوالی که مطرح می‌شود این است که چگونه مطمئن هستیم که روش‌های مختلف تولید عدد تصادفی، واقعا اعداد تصادفی تولید کرده‌اند. آیا واقعا اعداد تصادفی تولید شده توسط الگوریتم‌ها، دستگاه‌های الکترونیکی و ... تصادفی هستند.

در این نوشتار به بررسی علت نیاز به اعداد تصادفی، تاریخچه تولید آن‌ها و کاربردهایشان می‌پردازیم. از آنجایی که معمولا در تولید اعداد تصادفی از توزیع یکنواخت (گسسته) استفاده می‌شود، مطالعه نوشتار توزیع یکنواخت گسسته و پیوسته — مفاهیم و کاربردها خالی از لطف نیست.

اعداد تصادفی (Random Numbers)

چگونه می‌توان پدیده تصادفی (Random Phenomena) را تشخیص داد؟ آیا همه پدیده‌های طبیعی تصادفی هستند؟ از آنجایی که پدیده‌های تصادفی، غیرقابل پیش‌بینی هستند، زیبا به نظر می رسند ولی مشکل آن است که استخراج و تشخیص پدیده‌های تصادفی طبیعی کاری سخت و پیچیده است.

فیلم آموزش محاسبات آماری در اکسل Excel در فرادرس

کلیک کنید

یکی از قدیمی‌ترین وسایل ایجاد پدیده‌های (اعداد) تصادفی که به دست انسان ساخته شده تاس (Dice) است. گالتون دانشمند و آمارشناس بزرگ در مجله Nature نوشته است:

«به عنوان یک ابزار انتخاب تصادفی، هیچ چیزی برتر از تاس وجود ندارد.»

وقتی تاس‌ها را تکان دهید و درون یک سبد بریزید، نتیجه نهایی و عدد مشاهده شده قابل پیش‌بینی نیست زیرا پدیده‌ها و علت‌های مختلفی بر روی مشاهده نهایی تاثیر دارند. برخورد تاس‌ها با یکدیگر، برخورد تاس‌ها با سطح سبد و غیره بر نتیجه نهایی تاثیر گذار هستند. بنابراین می‌توان تاس را از اولین ابزارهای تولید اعداد تصادفی دانست که به دست بشر ساخته شده است.

 اعداد تصادفی و تاریخچه تولید

قدیمی‌ترین تاس کشف شده مربوط به 2400 سال قبل از میلاد در خاورمیانه است. همچنین در ۱۱۰۰ سال قبل از میلاد، در چین نیز لاک لاکپشت‌ها را حرارت می‌دادند تا به صورت تصادفی ترک بردارد. به این وسیله پیشگو‌ها دست به پیشگویی می‌زدند.

در سال‌های 1940، با ظهور کامپیوترها شیوه تولید اعداد تصادفی تغییر کرد. شرکت RAND به تولید ماشینی پرداخت که می‌توانست اعداد تصادفی را براساس پالس‌های تصادفی ایجاد کند. آن‌ها نتایج اعداد تصادفی تولید شده را در کتابی با عنوان «یک میلیون اعداد تصادفی با انحراف نرمال ۱۰۰ هزار» (A Million Random Digits with 100,000 Normal Deviates) به چاپ رساندند. این کتاب‌ امروز دوباره در سال ۲۰۰۱ برای علاقمندان بخصوص دانشمندان، محققین و ریاضی‌دان‌ها چاپ شده است.

یک رایانه دیگر نیز به نام ERNIE در دهه ۵۰ میلادی به تولید اعداد تصادفی پرداخت. از این اعداد به منظور قرعه کشی و تولید کدهای مربوط به کارت‌های بخت آزمایی استفاده می‌شد.

اعداد تصادفی و انواع آن

به عنوان یک تعریف می‌توان دستگاه تولید اعداد تصادفی را وسیله‌ای دانست که اعداد را به شکلی ایجاد می‌کند که دنباله این اعداد قابل پیش‌بینی نباشد. ممکن است چنین دستگاهی برمبنای پدیده‌های تصادفی فیزیکی یا شیمایی به تولید اعداد تصادفی بپردازد (مثل دستگاه ERNIE) که در اینصورت به آن‌ها به اختصار HRNG یا (Hardware Random Number Generator) گفته می‌شود. معمولا پدیده‌های تصادفی به کار رفته در این دستگاه‌ها وابسته به دما، اشعه کاتدی و ... هستند. اعداد تولید شده توسط چنین دستگاه‌هایی معمولا به نام TRNG یا (True Random Number Generator) معروفند.

ممکن است دستگاه تولید اعداد تصادفی براساس روش‌های نرم‌افزاری و الگوریتم‌های شبیه‌سازی عمل کند که در این صورت این گونه ارقام را «اعداد شبه تصادفی» (Pseudo-Random Number) و دستگاه را «تولید کننده اعداد شبه تصادفی» (Pseudo-random Number Generators) یا PRNG می‌گویند.

الگوریتم‌های تولید اعداد شبه تصادفی

در آغاز دهه ۶۰ میلادی، الگوریتم‌ها و روش‌های محاسباتی برای تولید اعداد تصادفی توسط کامیپوترها ایجاد و به کار گرفته شد. ایده به کار گرفته شده در این الگوریتم‌ها از دستور العمل «آلن تورینگ» (Alan Turring) ریاضی‌دان و دانشمند انگلیسی استفاده شده بود. او بوسیله باز کردن پیام‌های رمزنگاری شده آلمان‌ها، نقش مهمی در جنگ جهانی دوم داشت.

از آنجایی که کار کردن و پیاده سازی الگوریتم تورینگ برای برنامه‌نویسان سخت و گاهی غیرممکن بود، بعدها، ایده جدیدی به نام الگوریتم «تولید اعداد شبه تصادفی» (Pseudo Random Number Generator) که به اختصار PRNG نامیده می‌شود، ظهور کرد. در این روش، از یک تابع ریاضی برای تولید اعداد تصادفی استفاده می‌شود.

با اجرای تکراری این گونه الگوریتم‌ها، ارقام یک عدد تصادفی تولید می‌شود. موضوع قابل توجه در مورد این روش آن است که اگر ورودی‌های یکسانی به این تابع داده شود، عدد تصادفی حاصل نیز یکسان خواهد بود. این ورودی که به عنوان مقدار اولیه برای تابع تولید اعداد تصادفی در نظر گرفته می‌شود به اصطلاح «دانه» (Seed) گفته می‌شود. به این ترتیب اگر هنگام تولید عدد تصادفی از مقدار seed یکسانی استفاده شود، نتایج نیز یکسان خواهد بود.

این ایده توسط «جان فون نویمان» (John Von Neumann) مطرح شد. او متوجه شد که اگر عدد اولیه seed را مربع کنیم و بخش میانی حاصل را انتخاب کنیم یک عدد تصادفی خواهیم داشت. این عدد تصادفی در مرحله بعدی به عنوان seed عمل کرده و مجددا به تولید عدد تصادفی دیگر می‌پردازد. در نتیجه اگر عدد seed شش رقمی باشد، اعداد تصادفی شش رقمی تولید خواهد شد که از لحاظ آماری می‌توانند تصادفی باشند به این معنی که این اعداد دارای توزیع یکنواخت گسسته هستند و دوره تکرار آن‌ها بسیار طولانی است.

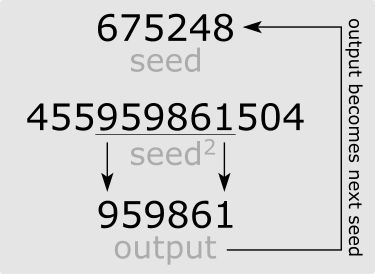
متاسفانه این روش با تکرارهای زیاد و یا انتخاب نادرست برای seed ممکن است دچار خطا شده و اعداد غیرتصادفی و به صورت چرخشی تولید کند. البته انتظار دیگری نیز از این الگوریتم نباید داشت زیرا مبنای محاسبه عدد تصادفی، برمبنای عدد قبلی است. بنابراین اگر با بزرگ انتخاب کردن عدد seed چرخه را طولانی و طولانی‌تر کنیم، عملا به اعداد تصادفی دست پیدا خواهیم کرد. در تصویر زیر، چرخه مربوط به این الگوریتم قابل مشاهده است.

«لهمر» (D. H. Lehmer) ریاضی‌دان آمریکایی از ایده «نویمان» استفاده کرد و در سال 1949 روشی به نام «تولید همسان خطی» (Linear Congruential Generator) را معرفی کرد. این روش به اختصار LCG نامیده می‌شود. در این روش از رابطه بازگشتی زیر استفاده می‌شود.

$$\large R_{n+1}=(aR_n+b) \mod m$$

 در این رابطه منظور از mod محاسبه باقی‌مانده تقسیم (aR_n+b) بر m است. در این حالت a ضریب و b میزان افزایش است. در ادامه کد مربوط به «جاوا» (Java) برای تولید اعداد تصادفی که به نام Central Randomize معروف است نوشته شده.

1// The Central Randomizer 1.3 (C) 1997 by Paul Houle (paul@honeylocust.com)
2// See:  http://www.honeylocust.com/javascript/randomizer.html
3rnd.today=new Date();
4rnd.seed=rnd.today.getTime();
5function rnd() {
6  rnd.seed = (rnd.seed*9301+49297) % 233280;
7  return rnd.seed/(233280.0);
8};
9
10function rand(number) {
11  return Math.ceil(rnd()*number);
12};

معمولا مقدارهای مربوط به پارامترهای a و b را اعداد اول در نظر می‌گیرند. همچنین مقدار m نیز دوره تکرار (Period) را مشخص می‌کند. این الگوریتم و کد در زبان جاوا در بسیاری از برنامه‌ها مورد استفاده قرار گرفت زیرا در زبان جاوا تابعی برای تولید اعداد تصادفی وجود نداشت.

اعداد تصادفی و کاربردهای آن‌

تا قبل از به کارگیری اعداد تصادفی در اینترنت، محیط مرورگرها امن نبود تا اینکه در سال ۱۹۹۵ پرتکل SSL و روش‌های رمزنگاری اطلاعات در اینترنت بوسیله الگوریتم پیشرفته PRNG معرفی شد. در بیشتر CPU های رایانه‌های دهه ۹۰ میلادی، دستور العملی برای تولید اعداد تصادفی وجود نداشت و بوسیله الگوریتم‌هایی که بر مبنای seed کار می‌کردند اعداد شبه تصادفی ایجاد می‌شد. به همین علت سرورهای وب Netscape از ترکیب ID و زمان استفاده کاربر، برای تولید seed استفاده می‌کردند. در این میان «بیکر» (Phillip Hallam-Baker) به عنوان یک دانشمند علوم رایانه کشف کرد که یک هکر می‌تواند به عنوان یک مهاجم، با استفاده از حدس‌های مختلف برای مقدار seed و محاسبات ساده، به رمز‌های رایانه‌ها دسترسی پیدا کند.

در سال 1999، شرکت اینتل یک مدار تولید اعداد تصادفی بر روی سرور i810 خود قرار داد. این مدار الکترونیکی براساس تغییرات دمایی، به تولید اعداد تصادفی واقعی می‌پرداخت. متاسفانه دستگاه‌ها و روش‌های تولید اعداد تصادفی واقعی (TRNG) نسبت به روش‌های شبه‌تصادفی (PRNG) کندتر هستند به همین علت الگوریتم‌های تولید اعداد تصادفی از محبوبیت و البته دقت کمتری نسبت به روش‌های واقعی برخوردارند.

در سال 2012 شرکت اینتل برمبنای همان روشی که در i810 ارائه داده بود، دو دستورالعمل RDRAND و RDSEED را به عنوان روش TRNG معرفی کرد که نرخ ۵۰۰ مگابایت در ثانیه برای تولید اعداد تصادفی دارد. متاسفانه شرکت اینتل در مورد روشی که برای تولید اعداد تصادفی در تابع RDRAND به کار رفته، توضیحی نداده است.

امروز دستگاه‌های تولید اعداد تصادفی واقعی TRNG به صورت سخت‌افزارهای متن باز نیز قابل دستیابی هستند. به این ترتیب شفافیت در نحوه کار دستگاه‌های TRNG به صورت یک نهضت به پیش‌ می‌رود. REDOUBLER یکی از این گونه برنامه‌ها است که کد آن در GitHub (+) قابل دسترس است.

انتخاب روش تولید عدد تصادفی و شیوه پیاده‌سازی آن هنوز جای بحث دارد. بخصوص برای کسانی که در حال توسعه نرم‌افزارهای هسته سیستم عامل یا زبان برنامه نویسی هستند، اطلاع از روش‌های تولید عدد تصادفی اهمیت دارد. همچنین رمزنگاری و پرتکل‌های امن مثل OpenSSL یا OpenSSH وابسته به شیوه‌های مطمئن در تولید اعداد تصادفی هستند. الگوریتم‌های تولید عدد تصادفی با توجه به تنوع شیوه محاسبات و نرخ تولید ارقام تصادفی با یکدیگر به رقابت می‌پردازند. ولی در سطح ابتدایی و نیمه حرفه‌ای با استفاده از تابع $$rand()$$ در بیشتر زبان‌های برنامه نویسی و برنامه‌های کاربردی می‌توان به تولید عدد تصادفی پرداخته و از این شیوه برای اموری که از سطح امنیت خیلی بالایی برخودار نیستند، بهره گرفت.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش Cryptography در دات نت
• آموزش آمار و احتمال مهندسی
• آموزش محاسبه انتگرال به کمک شبیه سازی مونت کارلو
• آزمایش تصادفی، پیشامد و تابع احتمال
• توزیع یکنواخت گسسته و پیوسته — مفاهیم و کاربردها