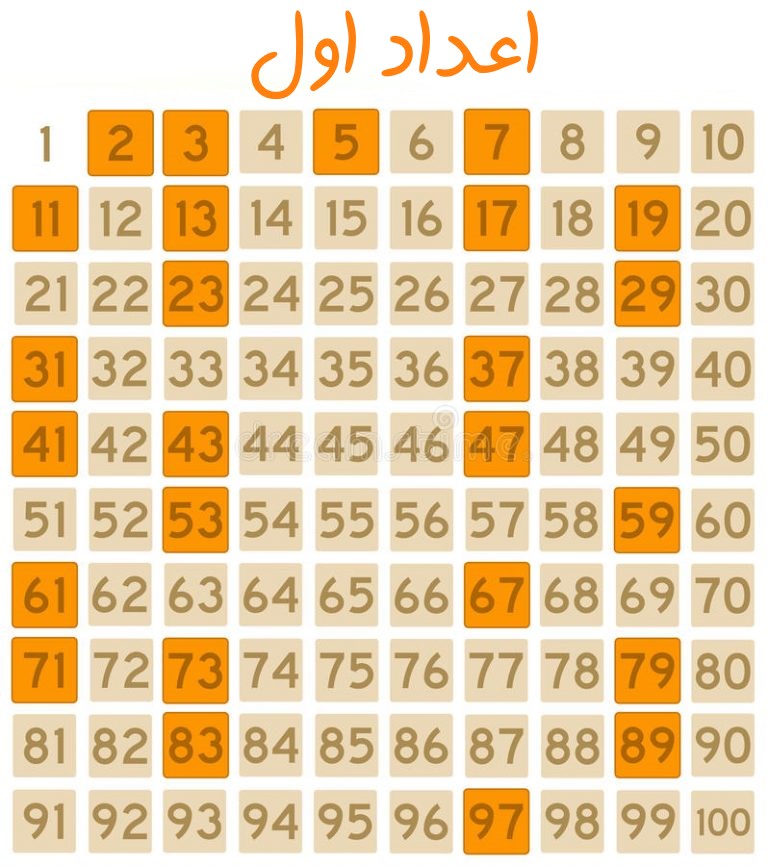
اعداد اول – به زبان ساده

در این مطلب از مجله فرادرس با اعداد آشنا می‌شویم. اعداد اول همانند چهره‌های مشهور در بین اعداد هستند. از آن‌ها در فیلم‌ها، کدهای امنیتی و معماها استفاده می‌شود و حتی اساتید دانشگاهی نیز با نگاهی حسرت‌بار به آن‌ها می‌نگرند. ریاضیدان‌ها مشغول یافتن بزرگترین عدد اول هستند. آن‌ها تاکنون 20 میلیارد عدد اول را شناسایی کرده‌اند. بنابراین اجازه دهید افتخار یافتن بزرگ‌ترین عدد اول را به آنان واگذار کنیم و در این مقاله صرفاً به ارائه بینشی شهودی از اعداد اول بپردازیم.

در ادامه با ویژگی‌های اعداد اول آشنا خواهیم شد:

• اعداد اول آجرهای سازنده ساختمان اعداد محسوب می شوند. اعداد اول در ریاضیات مانند مولکول‌های مواد در شیمی هستند. همان‌طور که در شیمی با دانستن ساختار شیمیایی یک ماده می‌توانیم آن را تشخیص داده و خصوصیاتش را پیش‌بینی کنیم، در ریاضیات نیز اعداد اول چنین هستند.
• اعداد اول خصوصیات ویژه‌ای دارند. مثلاً تعیین آن‌ که عددی اول است کاری دشوار به نظر می‌رسد (باید توجه کنید که دشوار بودن نیز می‌تواند یک خصیصه مثبت باشد). این خصوصیات در رمزنگاری، چرخه‌ها و تعیین نحوه ضرب اعداد در یکدیگر مفید هستند.
• اعداد اول، بعضی از اعضای مجموعه اعداد طبیعی هستند.

اعداد اول چه هستند؟

یکی از اصول اولیه ریاضیات این است که هر عدد صحیحی را می‌توان به صوت حاصلضرب اعداد اول تجزیه کرد.

برای نمونه:

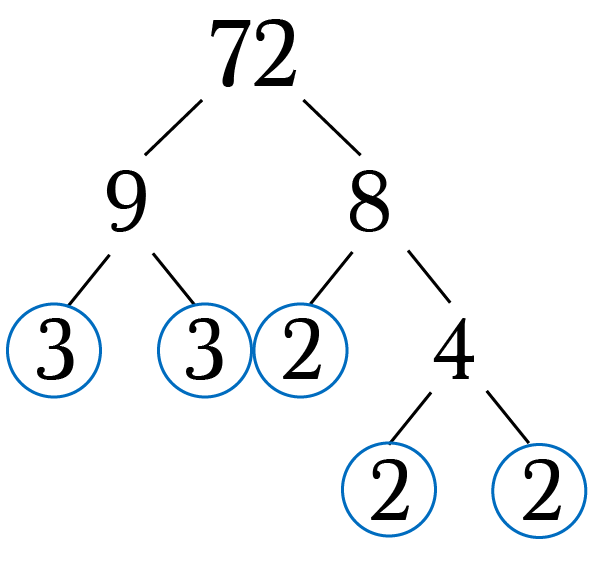
9 = 3 × 3 =3²

12 = 2 × 2 × 3 = 2² × 3

100 = 4 × 25 = 2 × 2 × 5 × 5 = 2² × 5²

مورد استثنا

اعداد اول اعدادی هستند که فقط به خودشان و ۱ بخش‌پذیر هستند و نمی‌توان آن‌ها را به عوامل دیگری غیر از این دو مورد تجزیه کرد. برای نمونه عدد ۲۴۱۵ را می‌توان به صورت حاصل ضرب اعداد اول 3، 5، 7 و 23 در نظر گرفت. حتی عدد 2 نیز اول است. اما عدد 1 چطور؟ پاسخ این است که 1 عدد خاصی است که اول در نظر گرفته نمی‌شود، چون در این صورت نتایج عجیبی به دست می‌آید مثلاً $$1=1\times 1\times 1\times \cdots =1^{\infty}$$ که باید آن را تعریف نشده در نظر گرفت. به همین علت حتی ریاضیدان‌ها نیز  1 را از این بحث استثنا می‌کنند و آن را عدد اول در نظر نمی‌گیرند.

بازنویسی یک عدد به صورت حاصلضرب اعداد اول، تجزیه به عوامل اول نامیده می‌شود که گاهی به آن، یافتن فاکتورهای اول نیز گفته می‌شود. تا این جا که اعداد اول ساده به نظر می‌رسند. اما باید بگوییم که نباید آن‌ها را ساده در نظر گرفت، چون مشخص شده است که:

• بی‌نهایت عدد اول وجود دارد و هرگز تمام نمی‌شوند.
• اعداد اول هیچ الگویی ندارند که بتوان آن را کشف کرد و برای مشخص کردن اول بودن یک عدد باید تقسیم‌های متوالی و زیادی را انجام داد.
• اعداد اول در اغلب موارد در جاهای عجیبی همچون مکانیک کوانتومی مشاهده می‌شوند.
• تجزیه یک عدد به عوامل اول دشوار است. معمولا این کار با تقسیم کردن خودِ عدد به اعداد اول انجام می‌شود که روشی طولانی محسوب می‌شود.

در هر صورت باید اذعان کنیم که توزیع اعداد اول کاملاً پیچیده است.

قیاس: اعداد اول و فرمول‌های شیمیایی

اعداد اول مانند اتم‌ها هستند. ما می‌توانیم هر عددی را بر اساس «فرمول شیمیایی» آن بازنویسی کنیم که اجزای آن را مشخص می‌کند. در شیمی، می‌توانیم بگوییم که مولکول آب در واقع همان H₂O است:

آب = H₂O= دو اتم هیدروژن و یک اتم اکسیژن

در مورد اعداد نیز می‌توانیم آن‌ها را به عوامل اولشان تجزیه کنیم. برای مثال عدد ۱۲ با تجزیه به عوامل اول به صورت زیر نوشته می‌شود:

12 = 2 × 2 × 3 = 2² × 3 = دو تا 2 و یک 3

می‌بینید قیاس جالبی به نظر می‌رسد. در حقیقت‌ ۲ها همانند H و ۳ همانند O است.

نکات جالب در اعداد اول

اما نکته جالب این قیاس چیست؟ وقتی شیمیدان‌ها عناصر اولیه خود را به صورت جدول تناوبی عنصر‌ها تنظیم کردند، ارتباطی میان عناصر یافتند که به صورت زیر است:

• عناصر جدید بر اساس جاهای خالی که در جدول بودند، پیش‌بینی شدند.
• عناصری که در ردیف و ستون یکسان بودند خصوصیات شیمیایی مشابهی داشتند.
• با حرکت در جهت‌های مختلف، روندهای خاصی (مانند افزایش واکنش‌پذیری) بروز و ظهور یافتند.

این نتایج و دستاوردها برای سازماندهی مجدد داده‌های از قبل موجود، چندان هم بد نیستند. می‌توانیم تصور کنیم که چه خوب می‌شود اگر اعداد اول را همانند عناصر در یک جدول قرار دهیم. اما برای این کار مشکلی وجود دارد.

هیچ کس نمی‌داند که جدول بایستی به چه شکل باشد! اعداد اول نامتناهی هستند و با این که ما قرن‌ها است که در جستجوی یافتن الگویی برای آن‌ها هستیم، اما موفق نبوده‌ایم. ما هیچ ایده‌ای در مورد این که شکاف بین اعداد اول چه اندازه می‌تواند باشد و یا این که عدد اول بعدی کجا ظاهر خواهد شد نداریم. این مسئله کاملاً واقعیت دارد و اگرچه فرضیه‌ها و حدس‌های جالبی در این خصوص وجود دارند، اما ما هنوز همه جزییات را نمی‌دانیم.

شیمی آلی و گروه‌های عاملی

هر کسی که اندک اطلاعاتی از شیمی داشته باشد، می‌تواند رابطه آن را با اعداد اول تشخیص دهد. در ادامه عناصر شیمیایی در قالب جدول تناوبی، نشان داده شده‌اند. 

عناصر شیمیایی بر اساس موقعیتشان در جدول تناوبی، خصوصیاتی دارند:

• اتم‌ها در گروه 8A (نئون و آرگون) گازهای نجیب هستند. این عناصر واکنشی با عناصر دیگر ندارند.
• اتم‌ها در گروه 4A (کربن و سیلیکون) اتصال‌پذیری خوبی دارند. این عناصر بلوک‌های تشکیل دهنده عناصر دیگر هستند.
• اتم‌ها در گروه 1 (سدیم، پتاسیم و غیره) بسیار واکنش‌پذیر هستند. این عناصر اگر در آب قرار بگیرند، منفجر می‌شوند.

در زمینه شیمی آلی ایده‌ای از گروه‌های عاملی وجود دارد: چند اتم می‌توانند دسته کل مولکول را تعیین کنند. برای نمونه:

• الکل‌ها زنجیره‌های خاصی از کربن-هیدروژن هستند که در انتهای خود دارای گروه OH هستند.
• متانول، اتانول و دیگر الکل‌ها خصوصیات مشابهی دارند و به همین دلیل گروه عاملی OH را تشکیل می‌دهند.

اکنون ببینیم اگر بخواهیم همین ایده را در مورد اعداد به کار بگیریم چه اتفاق رخ می‌دهد؟

مثال اول: حدس زدن زوج بودن

به طور کلی یک ماده شیمیایی آلی شامل کربن است (البته الزامی نیست ولی شروع خوبی محسوب می‌شود). مهم نیست که چه عناصری را با هم ترکیب می‌کنید؛ اگر هیچ گاه کربن را به این ترکیب اضافه نکنید، در این صورت نمی‌توانید یک ترکیب آلی بسازید.

فیلم آموزش مقدماتی نظریه اعداد – جامع و کاربردی در فرادرس

کلیک کنید

خصوصیت زوج بودن یک عدد نیز به همین ترتیب است. یک عدد در صورتی زوج است که در تجزیه خود عدد 2 را داشته باشد. یعنی از 2 برای تشکیل آن استفاده شده باشد. حال این عدد می‌تواند یک 2 باشد یا پنجاه تا 2 باشد. اگر فقط یک 2 در تجزیه هر عددی وجود داشته باشد، در این صورت عدد شما زوج است و در صورتی که نداشته باشید، عدد شما فرد است.

اینک می‌توانیم فرمول‌هایی که برای ضرب اعداد زوج و فرد در هم وجود دارد را مرور کنیم:

• عدد زوج × عدد فرد = عدد زوج.
• عدد زوج × عدد زوج = عدد زوج.
• عدد فرد × عدد فرد = عدد فرد.

فرمول اعداد اول

اگر بخواهیم این فرمول‌ها را بر حسب اعداد اول توضیح دهیم باید بگوییم که ضرب کردن، همان ترکیبِ «فرمول‌های عدد اول» است. از آنجا که اعداد زوج حامل فاکتور 2 هستند می‌توان حدس زد که:

• حاصل‌ضرب عددی زوج در یک عدد فرد بایستی زوج باشد، چراکه با یک 2 کار خود را آغاز کرده‌ایم و مهم نیست که پشت سر آن چه چیزی قرار دهیم.
• حاصلضرب عدد زوج در عدد زوج نیز عددی زوج است. در این مورد نیز اولین عامل عدد ما 2 است که معیار خوبی برای زوج بودن حاصلضرب است.
• اما حاصلضرب عدد فرد در عدد فرد باید فرد باشد. چون در هیچ کدام از آن‌ها عامل 2 وجود ندارد و نتیجه نیز فاقد 2 خواهد بود.

می‌بینید که یک نتیجه‌گیری ساده و جالب داریم. از آنجا که 2 عدد اول است، می‌دانیم که نمی‌توانیم آن را از حاصلضرب اعداد دیگر به دست آوریم. بدین ترتیب روش متفاوتی برای تفکر در مورد این مسئله یافتیم. اینک می‌توانیم پاسخ سؤالاتی مانند زیر را نیز به سادگی بدهیم:

حاصلضرب یک عدد فرد × عدد فرد × عدد فرد × عدد فرد × عدد زوج، عددی زوج خواهد بود یا فرد؟

بدیهی است که پاسخ زوج است، زیرا در گام آخر یک 2 را وارد ترکیب خود کرده‌ایم.

مثال دوم: پایان با صفر

احتمالاً از مشاهده نتیجه فوق هیجان‌زده شده‌اید و انتظار یک فرمول شیمیایی دیگر را دارید. این بار از گروه‌های عاملی کمک می‌گیریم. فرض کنید یک عدد، گروه عاملی به صورت 2 * 5 دارد یعنی یک یا چند 2 و یک یا چند 5 در میان عوامل خود دارد. برای نمونه:

10 = 2 × 5

40 = 2 × 2 × 2 × 5

90 = 3 × 3 × 2 × 5

آیا به این الگو توجه کردید؟ اگر عددی یک گروه عاملی 5 × 2 داشته باشد، حتماً رقم انتهایی آن 0 خواهد بود.

دلیل این حالت آن است که 5 × 2 = 10 است. بنابراین 5 × 2 × 2 × 2 مانند این است که داشته باشیم 10 × (2 × 2). هر عدد کامل ضرب در 10 شود رقم انتهایی‌اش 0 خواهد بود. به طور کلی حاصل‌ضرب عدد اول × (5 × 2) برابر با عددی است که رقم آخرش 0 خواهد بود.

بنابراین صرفاً با ملاحظه «فرمول اول» می‌توانیم رقم انتهایی حاصلضرب دو عدد را تشخیص دهیم و دیگر نیازی به انجام ضرب وجود ندارد.

مثال سوم: مجموع ارقام

در این بخش نیز یک مثال دیگر از گروه‌های عاملی ارائه می‌کنیم. اعدادی را تصور کنید که گروه عاملی «33» داشته باشند. یک عدد می‌تواند 400 تا 3 داشته باشد، اما تا زمانی که دست کم یک 2 داشته باشد، مطلوب ماست. اگر عددی عامل 3×3 را در خود داشته باشد، بدین معنی است که:

• بر 9 بخش‌پذیر است
• مجموع ارقام آن بر 9 بخش‌پذیر است.

برای نمونه عدد ۱۸ را در نظر بگیرید. این عدد را می‌توان به صورت زیر نوشت.

3 × 3 × 2 = 18

همان‌طور که در بالا نیز نشان داده شده، این عدد گروه عاملی 3 × 3 را در خود دارد. مجموع ارقام آن به صورت 1 + 8 = 9 است که بر 9 بخش‌پذیر است.

عدد عجیبی مانند 31 × 3 × 3 = 279 را در نظر بگیرید. این عدد نیز گروه عاملی 3 × 3 را دارد و مجموع ارقامش 2 + 7 + 9 = 18 است. 18 بر 9 بخش‌پذیر است و از این رو این عدد نیز خصوصیات فوق را دارد.

این خصوصیت نیز کاملاً جالب است. ما صرفاً با مشاهده یک خصوصیت معین به صورت گروه عاملی می‌توانیم در مورد مجموع ارقام یک عدد نظر بدهیم.

اعداد اول در زندگی روزمره

اعداد اول خصوصیاتی دارند که آن‌ها را مفید ساخته است.

فیلم آموزش اعداد اول در ریاضی – پایه هشتم (رایگان) در فرادرس

کلیک کنید

1. تجزیه اعداد به عوامل اول دشوار است

در واقع ما هنگام تجزیه یک عدد به عوامل اول، عملاً از روش آزمون و خطا استفاده می‌کنیم. یک روش این است که تلاش کنیم عدد را بر اعداد دیگر تا ریشه عدد تقسیم کنیم. این واقعیت که اعداد اول و تجزیه‌های عدد اول رمزآمیز هستند، می‌تواند سرنخ خوبی برای رمزنگاری باشد.

2. اعداد اول رابطه‌ای با اعداد غیر اول ندارند بلکه اعداد غیر اول با آن‌ها دارای رابطه‌اند

اعداد اول با اعداد غیر اول رابطه‌ای ندارند. ولی کوچکترین مضرب مشترک دو عدد برحسب اعداد اول آن‌ها نوشته می‌شود. برای نمونه 4 و 6 را در نظر بگیرید. کوچک‌ترین مضرب مشترک این دو عدد برابر با 12 است که البته از حاصلضرب آن‌ها یعنی ۲۴ کوچکتر است. با این حال کوچکترین مضرب مشترک برای اعداد اول از طریق ضرب آن‌ها بدست می‌آید. برای مثال کوچکترین مضرب مشترک 5 و 7 عددِ ۳۵ است که از طریق 35 = 7 × 5 حاصل می‌شود و هیچ مقدار دیگری کوچکتر از ۳۵ نمی‌تواند مضرب مشترک این دو باشد.

ممکن است فکر کنید که  عدم نظم در اعداد اول ممکن است چیز بدی باشد؛ اما این مسئله در طبیعت، یک مزیت محسوب می‌شود. حشره جیرجیرک هر 13 تا 17 سال یک بار از زیر زمین خارج می‌شود و این بدان معنی است که احتمال همپوشانی عمر آن با چرخه عمر جانور شکارچی‌اش (یعنی مضرب مشترک عمر آن‌ها) که ممکن است در چرخه رایج‌تر 2 یا 4 ساله قرار دارد کاهش می‌یابد و با احتمال زیاد، عمر بیشتری نیز خواهد داشت.

3. اعداد اول همه جا برتر هستند

در فیلم سینمایی تماس (1997) از اعداد اول به عنوان توالی‌هایی که در سراسر جهان درک می‌شوند یاد می‌شود. توالی اعداد اول (2، 3، 5، 7، 11، 13) یک توالی غیرمعمول است که تولید تصادفی آن دشوار است. برای مثال توالی 1، 0، 1، 0 می‌تواند توسط یک آونگ ایجاد شود در حالیکه به راحتی با دستگاه‌های مکانیکی نمی‌توان توالی اعداد اول را ایجاد کرد.

اعداد اول در هر سیستم عددی که باشند اول محسوب می‌شوند. 1/3 یک کسر با دوره گردش در مبنای 10 (0.33333) است و می‌توان استدلال کرد که عدد پی (3.14159...) در مبنای «$$\pi$$» یک عدد گنگ نیست. اما همه بر این نظر اتفاق دارند که اعداد اول در هیچ سیستم عددی قابل تقسیم به عوامل دیگر نیستند. اعداد اول را حتی می‌توان به یک سیستم عددی یکه که فاقد نقطه اعشاری است نیز انتقال داد:

II
III
IIIII
IIIIIII

بنابراین اعداد اول بی‌نهایت، غیرتکراری، و به صورت یک توالی درک شده جهانی هستند که برای ارسال پیام‌ها می‌توان از آن‌ها استفاده کرد.

نتیجه‌گیری

نباید به این دلیل که اعداد اول متفاوت هستند، از آن‌ها متنفر باشیم. در عوض ببینید که چه قدر خصوصیات مثبت دارند. عدم تطبیق در صورتی که قرار باشد به معنی عدم مواجهه با شکارچی باشد، هیچ گاه معنی نامناسبی نمی‌دهد! دشوار بودن تجزیه به عوامل سازنده، در صورتی که قرار باشد پیامی به صورت سری ارسال شود، خصوصیت بسیار خوبی محسوب می‌شود! برای مدتی طولانی اعداد اول صرفاً یک کنجکاوی نظری در نظر گرفته می‌شدند؛ اما چه موافق و چه مخالف مسلماً امروزه همگان اذعان دارند که این اعداد کاربردهای مفید زیادی دارند.

یکی از ویژگی‌های مهم ریاضیات نیز همین است که تشخیص دهد چگونه خصوصیات عجیب اعداد، می‌توانند در زندگی روزمره مفید باشند و هدف ما باید این باشد که دریابیم در کجا می‌توانیم از این قواعد بهره بگیریم.