معادله های پارامتری – به زبان ساده
جبر اساساً در مورد روابط است. چیزهای مختلف چگونه به هم وصل میشوند؟ آیا با هم حرکت میکنند یا حرکت جداگانهای دارند و یا کاملاً مستقل از هم هستند؟
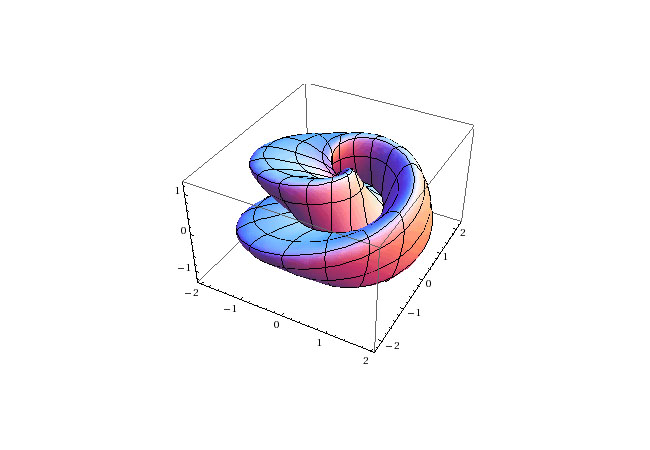
معادلههای معمولی یک اتصال ورودی به خروجی دارند. بدین ترتیب یک ورودی مانند x=3 میگیریم و در رابطه y=x2 نتیجه را به صورت y=9 میبینیم.
اما این تنها سناریوی ممکن نیست. فرمول y=x^2 نشان میدهد که y تنها به این دلیل حرکت میکند که x حرکت کرده است. اما آیا این امکان هست که هم y برابر با x^2 باشد و هم این که به طور همزمان عاملی پنهان هر دوی آنها را تغییر دهد. یعنی این عامل x را به 3 تغییر دهد و همزمان y را نیز برابر با 9 بسازد.
به عنوان یک مثال واقعی فرض کنید وقتی دمای هوا بالاتر از 21 درجه سلسیوس باشد، یک فروشگاه x عدد کرم ضد آفتاب و x^2 عدد بستنی میفروشد. رابطه جبری آن را میتوانیم به صورت زیر بنویسیم:
2(کرم ضد آفتاب) = بستنی
و با این که رابطه فوق ایرادی ندارد؛ اما گمراهکننده محسوب میشود.
این معادله بدین معنی است که کرم ضد آفتاب به طور مستقیم تقاضای بستنی را تغییر میدهد؛ در حالی که این عامل پنهان (دمای هوا) است که هر دوی آنها را تغییر داده است.
بهتر است که آنها را به صورت دو معادله جدا از هم بنویسیم:
21 - دما = کرم ضد آفتاب
2( 21 - دما) = بستنی
که علیت را نیز به خوبی نمایش میدهد. ایدههای «دمای هوا روی بستنی تأثیر دارد» و «دمای هوا روی کرم ضد آفتاب تأثیر دارد» وضعیت را به روشنی نشان میدهد و سعی میکند بخش «دما» ی مشترک را فاکتورگیری کند. معادلههای پارامتری به رابطه دنیای واقعی نزدیکتر است.
معادلههای پارامتری به زبان هندسی
در واقع معادلههای پارامتری مجموعهای از معادلهها هستند که یک مجموعه از مقادیر را به صورت تابعهای صریح از یک تعدادی متغیر مستقل بیان میکنند. این متغیرهای مستقل پارامتر نامیده میشوند.
دایره
برای نمونه گرچه معادله دایره در مختصات دکارتی به صورت R2 = x2+y2 است، اما میتوانیم با استفاده از یک مجموعه معادلههای پارامتری دایره را به صورت زیر توصیف کنیم:
X= r cos t
Y = r sin t
این معادلات پارامتری در شکل زیر نمایش یافتهاند:
توجه داشته باشید که بازنمایی معادلههای پارامتری معمولاً منحصر به فرد نیست. چون کمیتهای یکسان را میتوان به وسیله پارامترهای مختلف نشان داد. یک پارامتر منفرد معمولاً به وسیله t مشخص میشود،؛ در حالی که در معادلاتی که دو پارامتر دارند؛ معمولاً از حروف u و v استفاده میشود. معادلههای پارامتری روشی آسان برای نمایش دایرهها و سطوح هستند. برای مثال در ادامه معادلات پارامتری بیضی نیز به عنوان یک شکل دو بعدی ارائه شده است.
بیضی
بیضی در موقعیت کانونی خود (مرکز در مبدأ و قصر اصلی بیضی روی محور x های نمودار) و نیم قطرهای a و b به صورت معادلههای پارامتری زیر قابل نمایش است:
X = a cos t
y = b sin t
یک بیضی در موقعیت عمومی خود را میتوان به صورت زیر نمایش داد
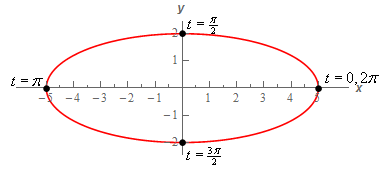
به زمان فکر نکنید، فقط به دلایل اصلی نگاه کنید
تقریباً همه آموزشهایی که در مورد معادلههای پارامتری وجود دارند از زمان به عنوان یک پارامتر نمونه استفاده میکنند. در واقع آن قدر این مثالهای معادلههای پارامتری با زمان همهگیر شدهاند که گاهی اوقات فراموش میکنیم معادلههای پارامتری در مورد زمان نیست؛ بلکه در خصوص علیت است.
اغلب معادلههای جبری رابطهای مانند y=x2 را نشان میدهند. معادلههای پارامتری باعث میشوند نگاه عمیقتری داشته باشیم؛ اما متأسفانه غالباً دچار همین ذهنیت زمان/فیزیکی هستیم. بدیهی است که در همه شرایط پارامتر پنهان وجود ندارد؛ اما موقعیتهای مختلف ارزش این بررسی را دارند.
اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد میکنیم موارد زیر را نیز بررسی کنید:
- مجموعه آموزشهای ریاضیات
- آموزش نرم افزار متمتیکا (Mathematica) برای حل معادلات ریاضی
- آموزش حل معادلات جبری و ریشه یابی در متلب
- آموزش طراحی پارامتریک و شبیه سازی حرکتی و ارگونومیک در کتیا (CATIA)
- آموزش های رایگان ریاضی و فیزیک
==



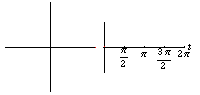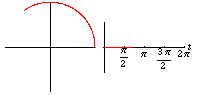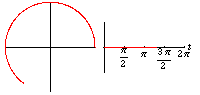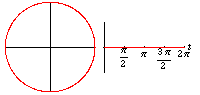











الان من کلاس یازدهم هستم رشتم ریاضیه معلم فیزیک من چرا باید این مبحث رو درس بده
اساساً دلیل این که ما از معادله های پارامتری استفاده می کنیم چیست مثلاً چه اشکالی دارد که همان معادله دایره را در دستگاه مختصات دکارتی بیان کنیم در واقع چه لزومی دارد که پارامترهای ایکس و y را از هم جدا کنیم و به صورت نسبت های مثلثاتی بنویسیم؟تشکر
خیلی ممنون مطالب بسیار روان قابل فهم و کاربردی بیان شده بودند. از زحمات شما سپاسگزاریم
بنظر من حل معادلات پارامتری، آسان تر از معادلات تحلیلی هست، و حجم محاسباتی کمتری هم دارد. برنامه های کامپیوتری مدلسازی سطحی و حجمی، از معادلات پارامتری برای رسم منحنی استفاده میکنند.
با سلام و احترام
یک سوال داشتم که جوابش خیلی برام مهمه. تصویر یا سایه یک دایره روی سطح چه شکلی میشه؟ آیا بیضی جوابه؟
ممنون از سایت خوبتون
میشه لطفا گوینده ی ویدئو هاتون رو عوض کنید
درود
خواهش میکنم .
همچنین خوشحال هستم از سایت عالی فرادرس
شاید خیلی مورد توجه نباشه اما سطر اول هم به جای یک اتصال ورودی به خروجی بک نوشته شده . با سپاس از فرادرس
سلام و وقت بخیر همراه عزیز فرادرس؛
از لطف شما سپاسگزاریم و به داشتن چنین خوانندگان دقیقی افتخار میکنیم. موردی که تذکر دادید، اصلاح شد.
متشکریم.
درود به فرادرس
سایت بسیار عالی ومفید من در وبگردی هم مقالات علمی فرادرس رو مطالعه میکنم
فقط در پاراگراف چهارم اشتباه شده کرم ضد اقتاب به طور مستقیم تقاضای بستنی رو افزایش میده.
با تشکر همیشگی از گروه عالی فرادرس
به امید هرروز پیشرفت و ترقی سایت و گروه فرادرس .
سلام.
متن اصلاح شد.
از بازخورد دقیقتان سپاسگزاریم و خوشحالیم که با مجله فرادرس همراه هستید.
شیوه بیان شما به خوبی مفهوم مورد نظر رو انتقال میداد.
بسیار سپاسگزارم 🙂