تنش نرمال و کرنش نرمال — آموزش جامع

تنش و کرنش به عنوان ابتدایی‌ترین مفاهیم مقاومت مصالح و مکانیک مواد به شمار می‌روند. در این مقاله، شما را یکی از ساده‌ترین انواع تنش و کرنش، یعنی تنش و کرنش نرمال آشنا خواهیم کرد.

در ابتدا به تعریف برخی از مفاهیم اولیه در رابطه با مبحث تنش و کرنش نرمال می‌پردازیم:

• تنش: معیاری است که نسبت نیروهای داخلی یک ماده بر واحد سطح را بیان می‌کند.
• کرنش: معیاری است که میزان تغییر شکل یک ماده نسبت به شکل اولیه آن را بیان می کند.
• میله منشوری: یک عضو سازه‌ای مستقیم است که سطح مقطع آن در امتداد طولش تغییری نمی‌کند.
• نیروی محوری: نیروی است که با اعمال در راستای محور عضو، باعث ایجاد کشش (افزایش طول) یا فشار (کاهش طول) می‌شود.

تنش نرمال

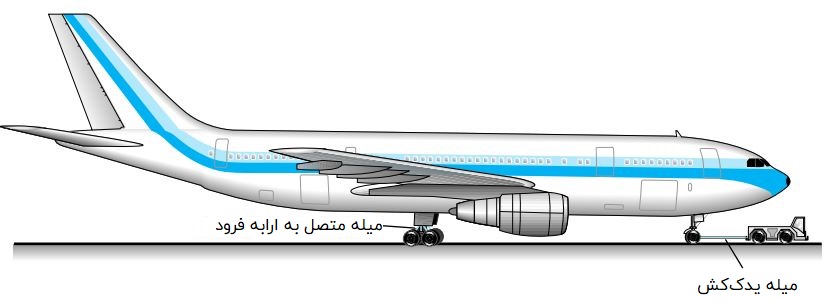
به منظور بررسی نحوه عملکرد تنش نرمال در قطعات مختلف، میله یدک‌کش در تصویر بالا را به عنوان یک مثال در نظر می‌گیریم. سپس، بخشی از این میله را انتخاب کرده و نمودار جسم آزاد این بخش را صرف نظر از وزن آن رسم می‌کنیم (شکل زیر). در این حالت، تنها نیروی اعمال شده بر این میله، نیروی محوری P خواهد بود.

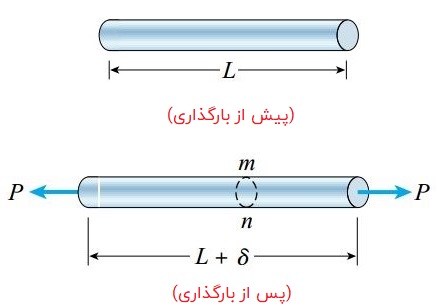
شکل زیر، میله بالا را در وضعیت پیش از اعمال بار و پس از اعمال بار نمایش می‌دهد. توجه داشته باشید که طول اولیه این میله با حرف L و تغییر طول آن با حرف یونانی دلتا (δ) مشخص شده است.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

با در نظر گرفتن یک مقطع فرضی مانند مقطع mn می‌توانیم فعل و انفعالات داخل میله را نمایش دهیم. از آنجایی که مقطع mn در راستای عمود بر محور طولی میله ایجاد شده است، به آن یک «مقطع عرضی» (Cross Section) گفته می‌شود.

اکنون بخش سمت چپ مقطع mn را به عنوان یک جسم آزاد در نظر می‌گیریم (شکل زیر). سپس سمت راست این جسم آزاد را حذف می‌کنیم و تنها عکس العمل آن نسبت به بخش باقی مانده را نمایش می‌دهیم. تنش‌های پیوسته اعمال شده بر روی سطح مقطع mn و نیروی محوری P (برآیند تنش‌ها)، به عنوان عکس العمل بخش حذف شده در نظر گرفته می‌شوند.

تنش با حرف یونانی سیگما (σ) نمایش داده می‌شود. به طور کلی، توزیع تنش اعمال شده بر روی یک سطح صاف می‌تواند به صورت یکنواخت یا متغیر باشد. فرض کنید که توزیع تنش بر روی سطح مقطع mn در شکل بالا یکنواخت است. به این ترتیب، برآیند این تنش‌ها با مقدار تنش ضرب در مساحت سطح مقطع میله برابر خواهد بود (P=σA). بنابراین، برای تعیین مقدار تنش‌های اعمال شده بر روی سطح مقطع میله می‌توان از رابطه زیر استفاده کرد:

معادله بالا، شدت تنش یکنواخت در حین بارگذاری محوری بر روی یک میله منشوری با شکل مقطع دلخواه را نمایش می‌دهد. در صورتی که میله بر اثر اعمال نیروهای P تحت کشش قرار گرفته باشد، «تنش کششی» (Tensile Stress) و در صورتی که تحت فشار قرار گرفت باشد، «تنش فشاری» (Compressive Stress) به وجود می‌آید. به دلیل اعمال تنش‌های کششی و فشاری در امتداد عمود بر سطح مقطع میله، به آن‌ها «تنش‌های نرمال» (Normal Stresses) گفته می‌شود. در نتیجه، تنش‌های نرمال یا به صورت کششی و یا به صورت فشاری هستند.

با توجه قواعد علامت‌گذاری، معمولاً علامت مثبت برای تنش کششی و علامت منفی برای تنش فشاری مورد استفاده قرار می‌گیرد. از آنجایی که تنش نرمال σ از تقسیم نیروی محوری بر مساحت سطح مقطع به دست می‌آید، یکای آن معادل نیرو بر واحد سطح است.

به عنوان مثال، میله‌ای با قطر 2 اینچ (in) را در نظر بگیرید که تحت بار 6 کیلو پوند (kip) قرار گرفته است. تنش نرمال درون این میله برابر به صورت زیر محاسبه می‌شود:

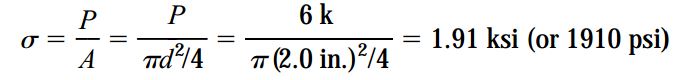
در این مثال، تنش به صورت کششی یا مثبت است. در سیستم آمریکایی (مانند مثال بالا)، مقدار تنش با واحد پوند بر اینچ مربع (psi) یا کیلو پوند بر اینچ مربع (ksi) بیان می‌شود.

در سیستم SI، برای بیان نیرو از واحد نیوتن (N) و برای بیان مساحت از واحد متر مربع (m²) استفاده می‌شود. به این ترتیب، واحد تنش در سیستم SI برابر با نیوتن بر متر مربع (N/m²) یا پاسکال (Pa) خواهد بود. توجه داشته باشید که پاسکال یک واحد کوچک به شمار می‌رود. از این‌رو، در اکثر مسائل واقعی به منظور بیان مقدار تنش از واحد مگاپاسکال (MPa) استفاده می‌شود. واحد نیوتن بر میلی‌متر مربع (N/mm²) معادل واحد مگاپاسکال است.

توجه: 1psi=6895Pa

بنابراین، اگر بخواهیم مثال بالا را در سیستم SI حل کنیم، جواب مسئله برابر با 13.2x10⁺⁶ پاسکال یا 13.2 مگاپاسکال خواهد بود.

محدودیت‌های استفاده از رابطه تنش نرمال

کاربرد اصلی رابطه σ=P/A برای مواقعی است که تنش‌های موجود بر روی سطح مقطع میله دارای توزیع یکنواخت باشند. این شرط زمانی تحقق می‌یابد که نیروی محوری P بر مرکز هندسی سطح مقطع اعمال شود. اگر نیروی P بر روی مرکز هندسی سطح مقطع اعمال نشود، میله با خمش مواجه خواهد شد. در نتیجه، برای ارزیابی این شرایط به تحلیل‌های پیچیده‌تری نیاز خواهد بود. معمولاً در مسائل کاربردی فرض می‌شود که شرط بالا برقرار است؛ مگر اینکه خلاف آن در گزارش‌ها بیان شده باشد.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

در شکل زیر، شرط یکنواخت بودن توزیع تنش برای تمام طول میله به جز انتهای آن صادق است. توزیع تنش در انتهای یک میله به نحوه انتقال بار P به درون آن بستگی دارد. اگر این بار به صورت یکنواخت به انتهای میله وارد شود، الگوی تنش در این ناحیه با دیگر نواحی تفاوتی نخواهد داشت. اگرچه، در صورت اعمال بار به صورت نقطه‌ای (از طریق یک میخ یا پیچ)، ناحیه‌ای با تجمع بالای تنش در انتهای میله به وجود می‌آید. به این ناحیه، «تمرکز تنش» (Stress Concentration) گفته می‌شود.

در شکل زیر، نمونه‌ای از یک نوع بارگذاری با احتمال وجود تمرکز تنش نمایش داده شده است. در این مثال، بارهای P به وسیله میخ‌های عبوری از حفره‌های انتهای میله به درون جسم اعمال می‌شوند. نیروهای نمایش داده شده، برآیند فشارهای تکیه‌گاهی بین میخ و میله هستند. در این حالت، تمرکز تنش به وجود آمده در اطراف حفره‌های میله وضعیت پیچیده‌ای دارد. اگرچه، با فاصله گرفتن از انتهای میله و حرکت به سمت مرکز آن، توزیع تنش به طور تدریجی یکنواخت می‌شود.

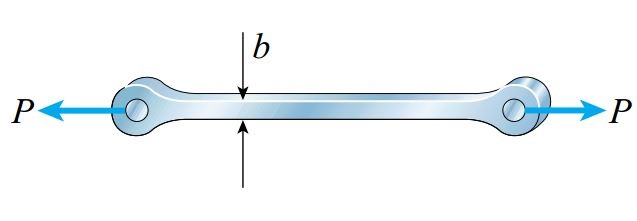
به عنوان یک قانون کاربردی به خاطر داشته باشید که به کارگیری رابطه σ=P/A برای نقاط درون یک میله منشوری در صورتی از دقت خوبی برخوردار خواهد بود که این نقاط از محل تمرکز تنش به اندازه کافی (در امتداد بزرگ‌ترین بعد میله) فاصله داشته باشند. به عبارت دیگر، توزیع تنش در مثال بالا برای فاصله b یا فواصل بیشتر از b یکنواخت است. b با عرض میله برابری می‌کند. در شکل زیر، توزیع تنش برای فاصله d یا فواصل بیشتر از d نسبت به دو انتهای میله به صورت یکنواخت خواهد بود. d با قطر میله برابر است.

توجه: لازم به ذکر است که رابطه σ=P/A در هنگام غیر یکنواخت بودن توزیع تنش نیز قابل استفاده است زیرا این رابطه، مقدار تنش نرمال میانگین بر روی سطح مقطع را تعیین می‌کند.

کرنش نرمال

هنگامی که یک میله مستقیم تحت بارگذاری محوری قرار می‌گیرد، طول آن در صورت اعمال کشش افزایش و در صورت اعمال فشار کاهش می‌یابد. میله منشوری زیر را به عنوان یک مثال در نظر بگیرید. میزان افزایش طول یا کشیدگی (δ) این میله، از جمع کشیدگی تمام اجزای ماده سازنده آن به دست می‌آید. فرض کنید که ماده سازنده میله در تمام نقاط یکسان است. به این ترتیب، در صورت در نظر گرفتن نصف طول میله (L/2)، میزان کشیدگی برابر با δ/2 و در صورت در نظر گرفتن یک چهارم طول میله، میزان کشیدگی برابر با δ/4 خواهد شد.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

به طور کلی، کشیدگی یک بخش با تقسیم طول آن بر طول کل (L) و ضرب نسبت به دست آمده در کشیدگی کل (δ) تعیین می‌شود. بنابراین، کشیدگی بخشی از میله با طول واحد (1 متر، 1 سانتی‌متر، 1 میلی‌متر یا ...) برابر حاصل‌ضرب معکوس L در δ خواهد بود. این کمیت با عنوان کشیدگی بر واحد طول یا «کرنش» (Strain) شناخته شده و با حرف یونانی اپسیلون (‎ε) نمایش داده می‌شود. رابطه زیر برای محاسبه کرنش مورد استفاده قرار می‌گیرد:

در صورتی که میله تحت کشش قرار گرفته باشد، «کرنش کششی» (Tensile Strain) و در صورتی که میله تحت فشار قرار گرفت باشد، «کرنش فشاری» (Compressive Strain) به وجود می‌آید. معمولاً برای کرنش کششی علامت مثبت و برای کرنش فشاری علامت منفی در نظر گرفته می‌شود. از آنجایی که کرنش ε در اثر اعمال تنش نرمال به وجود می‌آید، به این کمیت «کرنش نرمال» (Normal Strain) می‌گویند.

کرنش نرمال یک کمیت بدونِ بعد به شمار می‌رود زیرا از تقسیم دو کمیت با واحد یکسان به دست می‌آید. کمیت‌های بدون بعد هیچ واحدی ندارند و تنها به وسیله یک عدد نمایش داده می‌شوند. معمولاً در میله‌هایی که از مواد سازه‌ای ساخته می‌شوند، مقادیر عددی کرنش بسیار کوچک است؛ چراکه طول این مواد در هنگام قرارگیری در معرض بارگذاری به مقدار کمی تغییر می‌کند. به عنوان مثال اگر یک میله فولادی با طول 2 متر تحت بارگذاری کششی قرار گیرد، طول آن به اندازه 1.4 میلی‌متر افزایش می‌یابد. با در نظر گرفتن این مقادیر، کرنش این میله برابر است با:

در مسائل واقعی، واحدهای اصلی δ و L در کنار کرنش ذکر می‌شوند. به این ترتیب، کرنش در کنار عباراتی نظیر میلی‌متر بر متر (mm/m)، میکرومتر بر متر (μm/m) و اینچ بر اینچ (in/in) ثبت می‌شود. به عنوان مثال، مقدار کرنش در مسئله بالا را می‌توان به صورت 700μm/m یا 700x10^-6in/in بیان کرد. به علاوه، کرنش در برخی از مواقع (بخصوص در هنگام بزرگ بودن مقدار آن) به شکل درصد بیان می‌شود. به عنوان مثال، مقدار کرنش در مسئله بالا، 0.07 درصد است.

تنش و کرنش تک‌محوری

مفاهیم تنش نرمال و کرنش نرمال بر اساس ملاحظات هندسی و استاتیکی محض تعریف می‌شوند. از این‌رو، روابط ارائه شده در بخش‌های قبل را می‌توان برای تمام مقادیر بارگذاری و هر نوع ماده‌ای مورد استفاده قرار داد. به این منظور باید تمام شرط‌های زیر برقرار باشند:

• همسانگرد بودن ماده (یکنواخت بودن تغییر شکل در تمام نقاط)
• منشوری بودن هندسه (یکسان بودن سطح مقطع در طول ماده)
• اعمال بار بر روی مرکز هندسی مقاطع
• همگن بودن ماده (یکسان بودن مواد سازنده در تمام نقاط)

با برقرار بودن شرط‌های، حالت به دست آمده برای تنش و کرنش با عنوان «تنش و کرنش تک‌محوری» (Uniaxial Stress and Strain) شناخته می‌شود.

خط اثر نیروهای محوری برای توزیع تنش یکنواخت

در مطالب ارائه شده راجع به تنش و کرنش درون یک میله منشوری، فرض کردیم که تنش نرمال σ به صورت یکنواخت بر روی سطح مقطع میله توزیع شده است. این حالت زمانی رخ می‌دهد که خط اثر نیروهای محوری از مرکز هندسی سطح مقطع عبور کرده باشد.

فیلم مجموعه آموزش تحلیل و طراحی سازه‌ ها – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

شکل زیر، یک میله منشوری با سطح مقطعی به شکل دلخواه را نمایش می‌دهد که تحت نیروهای محوری P قرار گرفته است. تنش‌های ناشی از اعمال نیروهای P دارای توزیع یکنواخت هستند. نقطه p₁، بر روی محل تقاطع نیروها با سطح مقطع قرار دارد. با ایجاد یک دستگاه مختصات xy در صفحه دربرگیرنده سطح مقطع می‌توان مختصات نقطه p₁ را با ^-x^- و ^-y^- مشخص کرد.

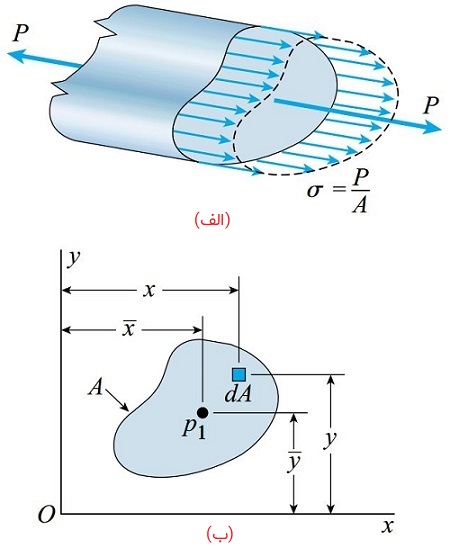
برای تعیین این مختصات، باید گشتاور M_x و M_y حاصل از نیروی P حول محور x و y را با گشتاورهای حاصل از تنش‌های یکنواخت برابر قرار داد. رابطه گشتاور حاصل از نیروی P برابر است با:

در روابط بالا، گشتاوری مثبت در نظر گرفت می‌شود که بردار آن در جهت مثبت محور مربوطه اعمال شود. گشتاور تنش‌های توزیع شده از طریق انتگرال‌گیری بر روی مساحت سطح مقطع (A) به دست می‌آید. نیروی تفاضلی اعمال شده بر روی المان سطح dA با حاصل σdA برابر است. گشتاورهای حاصل از این نیروی جزئی حول محورهای x و y به ترتیب با σ_ydA و σ_xdA- برابر هستند. در این روابط، x و y مختصات المان dA را نمایش می‌دهند. مقدار گشتاور کل از طریق انتگرال‌گیری از سطح مقطع به دست می‌آید:

در روابط بالا، گشتاورهای حاصل از تنش‌های σ محاسبه می‌شوند. در مرحله بعد باید گشتاورهای M_x و M_y حاصل از نیروی P را برابر با روابط بالا قرار داد:

از آنجایی که توزیع تنش‌های σ یکنواخت است، مقادیر آن‌ها بر روی سطح A تغییر نمی‌کند. به همین دلیل، پارامتر A را می‌توان از درون انتگرال خارج کرد. علاوه بر این، با جایگذاری P/A به جای σ در روابط بالا خواهیم داشت:

معادلات بالا با روابط موجود برای تعیین مختصات مرکز هندسی یک سطح برابر هستند. بنابراین می‌توان نتیجه گرفت که به منظور اعمال فشار یا کشش یکنواخت بر یک میله منشوری، نیروی محوری باید از مرکز هندسی مساحت سطح مقطع میله عبور کند. در اکثر مواقع فرض می‌شود که این شرط برای مسئله مورد بررسی برقرار است.

مثال‌های کاربردی

در ادامه نحوه محاسبه تنش و کرنش موجود در میله‌های منشوری را با ارائه دو مثال تشریح می‌کنیم. در مثال اول، وزن بار نادیده گرفته شده اما در مثال دوم این پارامتر نیز به مسئله اضافه می‌شود.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

مثال 1

یک لوله مدور توخالی از جنس آلومینیوم مطابق شکل زیر تحت بار فشاری 26k (کیلو پوند) قرار دارد. قطر داخلی و خارجی لوله به ترتیب .d₁=4in و .d₂=4.5in و طول آن برابر .L=16in است. طول لوله پس از اعمال فشار به اندازه .0.012in کاهش می‌یابد. با توجه به اطلاعات مسئله، میزان تنش و کرنش فشاری را تعیین کنید. (از وزن لوله و همچنین از احتمال کمانش آن صرف نظر شده است.)

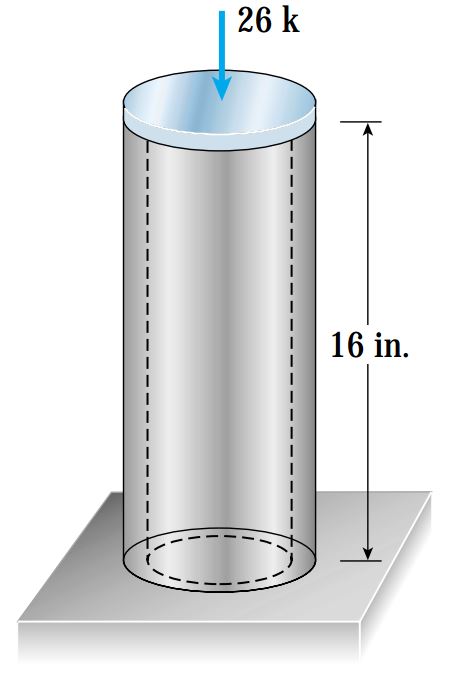
با فرض اعمال بار فشاری به مرکز لوله توخالی می‌توانیم از فرمول σ=P/A برای محاسبه تنش نرمال استفاده کنیم. نیروی P برابر با 26 کیلو پوند است و مساحت سطح مقطع لوله نیز از رابطه زیر به دست می‌آید:

بنابراین، برای تنش فشاری خواهیم داشت:

کرنش فشاری نیز از طریق رابطه زیر قابل محاسبه است:

توجه: همان‌طور که در ابتدای مقاله توضیح داده شد، کرنش یک کمیت بدون بعد به حساب می‌آید و نیازی به نوشتن واحد در کنار آن نیست. اگرچه، برای ارائه اطلاعات بیشتر می‌توان واحد آن را نیز بیان کرد. به عنوان مثال در اینجا می‌توان ε را به صورت .ε=750x10^-6in/in یا .ε=750µin/in نوشت.

مثال 2

یک میله فولادی مدور با طول L و قطر d مطابق شکل زیر از یک چاه معدنی (شفت) آویزان شده است. این میله یک صندوق حاوی مواد معدنی با وزن W را در انتهای خود نگه می‌دارد.

• الف: رابطه تنش ماکسیمم σ_max در میله را با در نظر گرفتن وزن آن تعیین کنید.
• ب: اگر طول میله 40 متر، قطر آن 8 میلی‌متر و وزن آن 1.5 کیلو نیوتن باشد، مقدار تنش ماکسیمم چقدر خواهد بود؟

الف: نیروی محوری ماکسیمم F_max در انتهای بالایی میله رخ می‌دهد و مقدار با حاصل جمع وزن صندوق حاوی مواد معدنی W و وزن میله W₀ برابر است. وزن میله از حاصل‌ضرب وزن مخصوص در حجم آن به دست می‌آید:

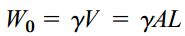
A، مساحت سطح مقطع میله را نمایش می‌دهد. بنابراین، رابطه تنش ماکسیمم به صورت زیر خواهد بود:

ب: برای محاسبه تنش ماکسیمم، مقادیر عددی را درون رابطه به دست آمده از قسمت اول سؤال جایگذاری می‌کنیم. d=8mm و وزن مخصوص فولاد (λ) برابر 77kN/m³ است. مساحت سطح مقطع A نیز از رابطه πd²/4 به دست می‌آید. بنابراین داریم:

توجه: در این مثال، وزن میله تأثیر قابل توجهی بر روی مقدار تنش ماکسیمم دارد. به همین دلیل نباید آن را نادیده گرفت.

^^