توزیع نرمال و توزیع نرمال استاندارد – به زبان ساده

در این مطلب از مجله فرادرس با توزیع نرمال و توزیع نرمال استاندارد آشنا می‌شویم. شاید تا کنون بارها عبارت «توزیع آماری» به گوش‌تان خورده باشد، ولی تصور دقیقی از معنی این اصطلاح نداشته باشید. پس از انجام هر نوع اندازه‌گیری همواره تعدادی داده (عدد) در اختیار داریم که می‌خواهیم ارتباط بین آنها را کشف کنیم یا آنها را دسته‌بندی نماییم تا بتوانیم آنها را تجزیه و تحلیل کنیم. برای انجام این کار ابتدا می‌بایست نحوه توزیع داده‌ها را بدانیم. به عبارت ساده‌تر توزیع داده‌ها به ما می‌گوید که پراکندگی و گستردگی داده‌هایی که جمع‌آوری کرده ایم چگونه است. توزیع نرمال نیز یکی از این الگوها است.

مثلاً اگر شما هر روز هفته صبح به ورزش می‌پردازید، توزیع زمان‌های ورزشی شما به صورت خطی است. داده‌ها ممکن است بسته به ماهیت آزمایش و عوامل گوناگون به انواع مختلفی توزیع یافته باشند. محققین معمولاً تلاش می‌کنند دریابند که توزیع داده‌ها به کدام توابع ریاضی نزدیک‌تر هستند، تا بدین ترتیب بتوانند تحلیل صحیحی از  ماهیت توزیع و محاسبات بر روی آن داشته باشند. یکی از مهم‌ترین توزیع‌های آماری، «توزیع نرمال» نام دارد.

نام دیگر توزیع نرمال، «توزیع طبیعی» یا «تابع گاوسی» است، زیرا این تابع را نخستین بار کارل فردریش گاوس پیشنهاد کرده است. این توزیع یکی از مهمترین توزیع‌های احتمالی پیوسته در نظریه احتمالات است. علت نام‌گذاری و همچنین اهمیت این توزیع، هم‌خوانی بسیاری از مقادیر حاصل شده، هنگام نوسان‌های طبیعی و فیزیکی پیرامون یک مقدار ثابت با مقادیر حاصل از این توزیع است. در ادامه انواع مختلفی از توزیع‌های محتمل داده‌ها را نشان داده‌ایم.

داده‌ها ممکن است طوری توزیع شوند که بیشتر در سمت راست باشند.

یا ممکن است این توزیع به گونه‌ای باشد که بیشتر در سمت چپ تجمع یابند.

همچنین ممکن است توزیع داده‌ها به صورت مختلط باشد.

اما موارد بسیاری وجود دارد که داده ها میل به جمع شدن در اطراف مقدار میانگین دارند. در چنین حالتی داده‌ها به سمت چپ یا راست تمایل ندارند، به این توزیع «توزیع نرمال» یا توزیع زنگوله‌ای‌ گفته می‌شود. مثل حالت زیر:

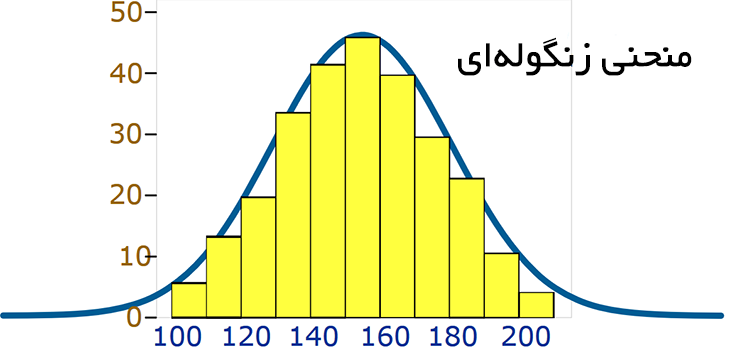
یک توزیع نرمال

«خمیدگی روی سطح زنگوله»، یک توزیع نرمال است. هیستوگرام زردرنگ در تصویر فوق برخی از داده‌ها را که به این منحنی نزدیک هستند نشان ‌می دهد. ممکن است در مواردی این داده‌ها کاملاً منطبق بر شکل زنگوله نباشد و این امری معمول و طبیعی است.

این توزیع بیشتر به نام «نمودار زنگوله‌ای» نیز نامیده می‌شود، زیرا شکل منحنی آن شبیه به یک زنگوله است.

موارد بسیاری وجود دارند که از توزیع نرمال تبعیت می کنند:

• قد افراد
• اندازه اجسام تولید شده ماشین‌آلات صنعتی
• خطاهای اندازه‌گیری
• فشار خون
• نمرات یک امتحان

در چنین مواردی می‌گوییم که داده‌ها «به صورت نرمال» توزیع یافته‌اند:

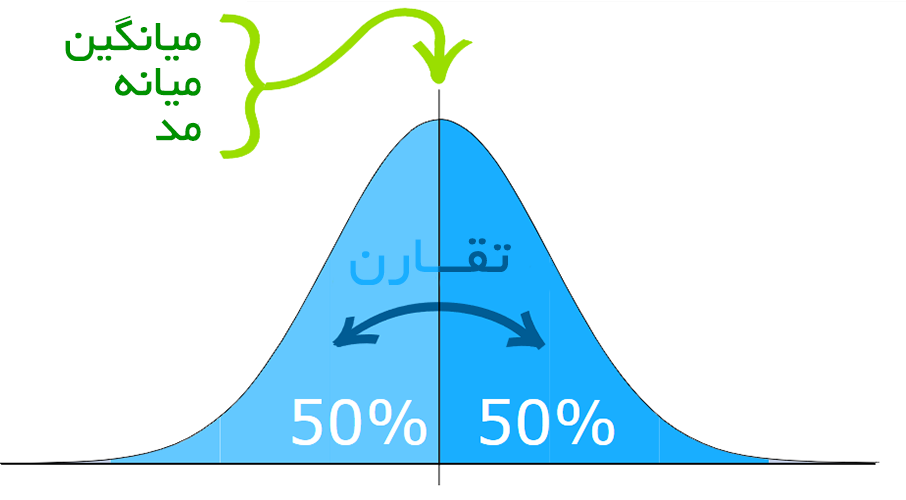
توزیع نرمال دارای موارد زیر است:

• میانگین = میانه = مد است.
• خط تقارن در وسط قرار می‌گیرد.
• %50 مقادیر، کوچکتر از میانگین و  %50 دیگر بزرگتر از میانگین هستند.

در آموزش‌های فرادرس، آمار و داده کاوی از موضوعات جذاب و مورد پسند محسوب می‌شوند. در آموزش آمار و احتمال مهندسی که توسط فرادرس منتشر شده است، سرفصل‌های مربوط به آموزش این درس در دانشگاه به طور کامل، پوشش داده شده و مثال‌ها به همراه نمونه آزمون کارشناسی ارشد، مورد بحث قرار می‌گیرد. لینکی که در ادامه مشاهده می‌کنید، برای دسترسی به این آموزش است.

انحراف معیار

انحراف معیار یا خطای استاندارد (Standard Deviation)، معیار پراکندگی اعداد است. هنگامی که انحراف معیار را اندازه‌گیری می کنیم، به طور معمول با موارد زیر مواجه می‌شویم:

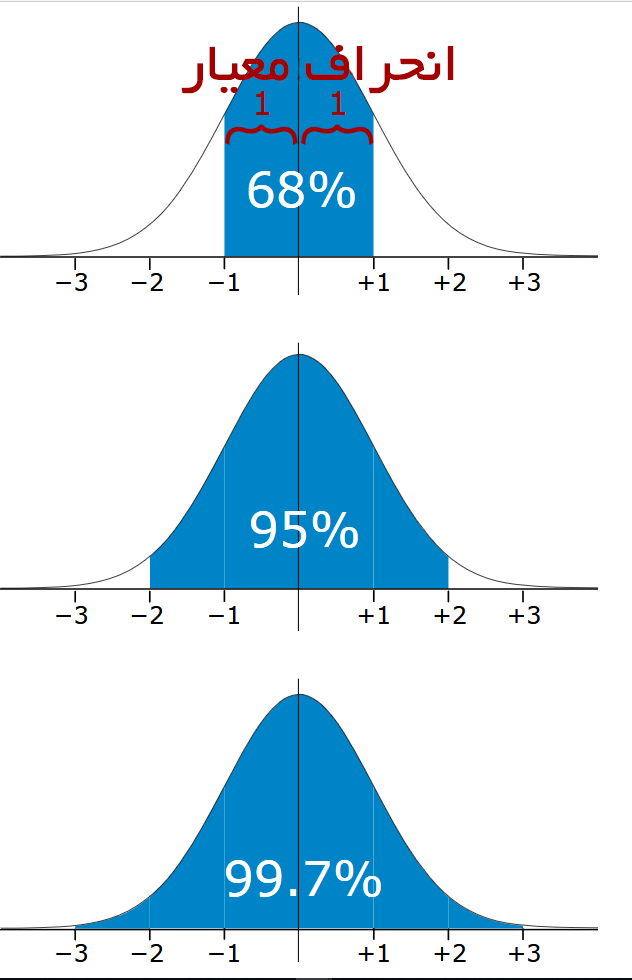
در تصویر اول می‌بینیم که 68% از مقدارها در محدوده یک انحراف معیار از میانگین هستند. در تصویر دوم، 95% از مقدارها در محدوده دو برابر انحراف معیار از میانگین هستند. در تصویر سوم، 99.7% از مقدارها در محدوده سه برابر انحراف معیار از میانگین هستند.

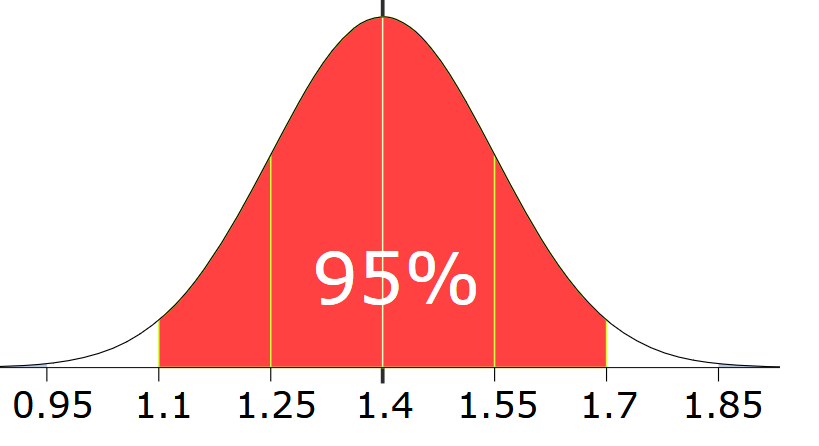
مثال: قد %95 از دانش آموزان در مدرسه بین 1.1 متر و 1.7 متر است. با در نظر گرفتن این که داده‌ها دارای توزیع نرمال هستند، چگونه می‌توان میانگین و انحراف معیار را به دست آورد؟ پاسخ بسیار ساده است. میانگین، در میان 1.1 متر و 1.7 متر است، پس:

= میانگین

(1.1m + 1.7m) / 2 = 1.4m

95%، برابر دو انحراف از معیار در طرفین میانگین است (مجموع 4 انحراف معیار)، پس:

= 1 انحراف معیار

(1.7m – 1.1m) / 4

= 0.6m / 4

= 0.15m

و نمودار حاصل به شکل زیر است:

دانستن انحراف معیار برای ما سودمند است، چون در آن صورت در مورد توزیع داده‌ها موارد زیر را می‌توانیم بیان کنیم:

• مقادیر ما به احتمال متوسط در محدوده یک برابر انحراف معیار از میانگین قرار دارند (68 از 100).
• مقادیر ما به احتمال زیاد در محدوده دو انحراف معیار از میانگین هستند (95 از 100)
• مقادیر ما تقریبا به احتمال بسیار زیاد در محدوده سه انحراف معیار حضور دارند (997 از 1000)

نمرات معیار

تعداد انحراف‌ها از میانگین همچنین با نام «نمره معیار یا نمره استاندارد» (Standard Score)، نیز نامیده می‌شود که به صورت «سیگما» و یا «نمره z» مورد اشاره قرار می‌گیرند.

مثال: در همان مدرسه مثال قبل، قد یکی از دانش آموزان برابر با 1.85 متر است.

در روی نمودار زنگوله ای، مشاهده می‌کنید که 1.85 متر، در محدوده  3 برابر انحراف از میانگین 1.4 متر قرار دارد.

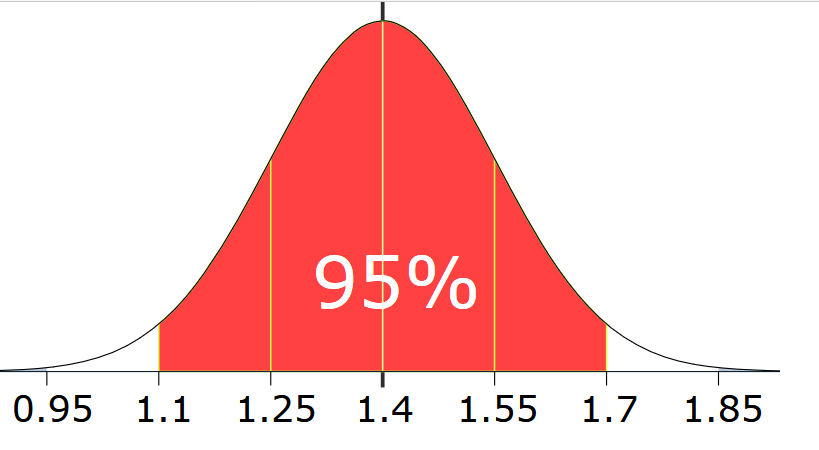
پس:

«نمره z» قد این دانش آموز برابر 3.0 است

همچنین می‌توان تعداد انحراف‌های عدد 1.85 از میانگین را محاسبه کرد. عدد 1.85 به چه مقدار از میانگین فاصله دارد؟

به اندازه 0.45 = 1.4 - 1.85 از میانگین فاصله دارد.

این مقدار فاصله برابر چند انحراف معیار است؟ انحراف معیار برابر 0.15 است، پس:

3 انحراف معیار = 0.45m / 0.15m

پس برای تبدیل یک مقدار به یک نمره معیار:

• ابتدا میانگین را از آن کم می کنیم،
• سپس بر مقدار انحراف معیار تقسیم می کنیم.

و انجام دادن این عمل را «استانداردسازی» می‌نامیم:

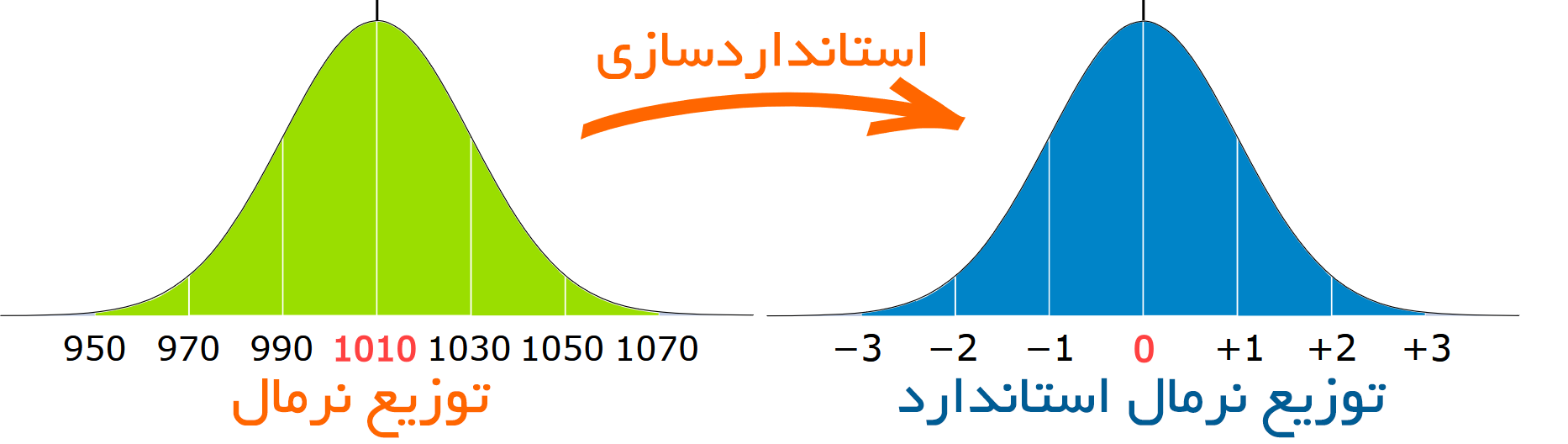
ما می‌توانیم هر توزیع نرمال را به توزیع نرمال استاندارد تبدیل کنیم.

مثال: زمان مسافرت

یک نظرسنجی از مدت زمان مسافرت، این مقادیر را نتیحه داده است (به دقیقه):

26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32, 28, 34

میانگین برابر 38.8 دقیقه و انحراف معیار نیز برابر 11.4 دقیقه است. مقادیر را به نمره های z یا نمرات استاندارد تبدیل کنید.

برای تبدیل 26:

• ابتدا مقدار میانگین را از آن کم کنید: 12.8- = 38.8 - 26
• سپس آن را بر مقدار انحراف معیار تقسیم کنید: 1.12 - = 11.4 / 12.8 -

پس عدد 26، 1.12- انحراف از میانگین دارد.

سه تبدیل اول را می توانید در زیر ببینید

و این سه تا را می توانید در نمودار مشاهده کنید:

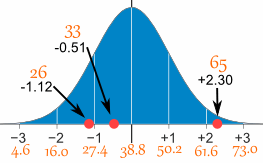
می توانید بقیه نمرات z را خودتان محاسبه کنید!

فرمول محاسبه نمره z در زیر آمده است:

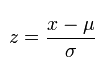
• z برابر «نمره z» (نمره معیار) است
• x مقداری است که باید استاندارد شود
• μ برابر میانگین است
• و σ برابر انحراف معیار می باشد

چرا از استانداردسازی استفاده می کنیم؟

استاندارد سازی می‌تواند به ما کمک کند که تصمیم‌هایی در مورد داده‌هایمان بگیریم. به مثال زیر توجه کنید.

مثال: پروفسور ویلوبی در حال تصحیح ورقه های دانشجویان است. نمرات دانش‌آموزان در زیر آمده است (از 60 نمره):

20, 15, 26, 32, 18, 28, 35, 14, 26, 22, 17

بسیاری از دانش‌آموزان حتی از 60 نمره، 30 نمره هم نگرفته‌اند و بیشترشان تجدید خواهند شد. امتحان باید بسیار سخت بوده باشد، پس پروفسور تصمیم می گیرد که تمامی نمرات را استاندارد کند و فقط آنهایی را که یک انحراف معیار پایین‌تر از میانگین نمره گرفته‌اند، تجدید اعلام کند. میانگین برابر 23 و انحراف معیار برابر 6.6 است و این مقادیر، نمرات استاندارد هستند:

-0.45, -1.21, 0.45, 1.36, -0.76, 0.76, 1.82, -1.36, 0.45, -0.15, -0.91

مشاهده می‌کنید که تنها 2 دانشجو تجدید خواهند شد (همان‌هایی که در امتحان 15 و 14 گرفته بودند).

از طرف دیگر استانداردسازی کارها را آسا‌ن‌تر می کند، چون در این حالت ما تنها به یک جدول نیاز خواهیم داشت (جدول توزیع نرمال استاندارد)، که دیگر نیازی به انجام محاسبات تک به تک برای فاصله هر مقدار از میانگین و انحراف استاندارد وجود ندارد.

جزئیات بیشتر

در تصویر زیر توزیع نرمال استاندارد را با درصد هایی برای هر نیمه از انحراف معیار، و درصد‌های تجمعی نمایش یافته است.

مثال: نمره شما در یک تست 0.5 انحراف معیار بیشتر از میانگین بود، چند نفر از شما کمتر نمره گرفته اند؟

• بین 0 و 0.5 برابر %19.1 است
• کمتر از 0 نیز برابر %50 است (نصف منحنی)

پس مجموع نمرات کمتر از نمره شما برابر است با:

50% + 19.1% = 69.1%

در تئوری، %69.1 کمتر از شما نمره گرفته اند؛ اما با داده‌های واقعی، درصد ممکن است، کمی متفاوت باشد.

مثال کاربردی برای بسته‌بندی شکر

فرض کنید شرکتی بسته‌های شکر را به صورت بسته‌های 1 کیلوگرمی بسته‌بندی می‌کند.

وقتی شما یک نمونه از کیسه‌ها را وزن می‌کنید، نتایج زیر به دست می‌آید:

• 1007 گرم، 1032 گرم، 1002 گرم، 983 گرم، 1004 گرم، ... (100 اندازه‌گیری)
• میانگین = 1010 گرم
• انحراف معیار = 20 گرم

اینک متوجه می‌شوید که برخی از مقادیر کمتر از 1000 گرم هستند. آیا می‌توانید این مشکل را حل کنید؟

توزیع نرمال اندازه‌گیری‌های شما به این شکل است:

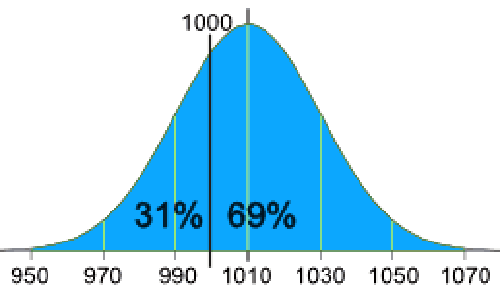
%31 از بسته‌ها کمتر از 1000 گرم وزن دارند، که در واقع فریب مشتری محسوب می‌شود.

این یک اتفاق تصادفی است، پس نمی توانیم بسته‌های کمتر از 1000 گرم شکر را متوقف کنیم؛ اما می‌توانیم تعداد آنها را به مقدار قابل توجهی کاهش دهیم. بدین منظور تنظیمات دستگاه بسته‌بندی را  در انحراف‌های معیار‌ مختلف  برای بسته‌های 1000 گرم بررسی می‌کنیم:

• در محدوده 3- برابر انحراف معیار:
  در منحنی زنگوله‌ای بزرگ مشاهده می‌کنیم که بسته‌ها در این محدوده %0.1‌ کم هستند؛ اما شاید این عدد بسیار کوچک باشد.
• در محدوده 2.5- انحراف معیار می‌بینیم :
  در بازه زیر 3 انحراف معیار، 0.1% و مابین انحراف‌های 3 و 2.5، %0.5 از بسته‌ها کم می‌شود که وقتی با هم جمع کنیم مقدار  %0.6 = %0.5 + %0.1 به دست می‌آید. این تنظیمات گزینه مناسبی برای انتخاب به نظر می‌رسد.

پس دستگاه را طوری تنظیم می کنیم که 1000 گرم را در محدوده 2.5- انحراف از میانگین داشته باشیم. اکنون، ما می توانیم به دو طریق تنظیم کنیم:

• مقدار شکر را در هر بسته افزایش دهیم، که میانگین را تغییر می‌دهد و یا
• دقت را افزایش دهیم که انحراف معیار را کاهش می‌دهد.

هر دو سناریو را امتحان کنیم.

تنظیم مقدار میانگین در هر بسته

انحراف معیار برابر 20 گرم است، و میانگین ما باید در محدوده  2.5 برابری از آن قرار گیرد:

2.5 × 20g = 50g

پس دستگاه باید میانگین 1050 گرم را نتیجه دهد:

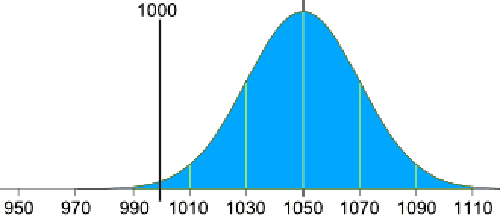
تنظیم دقت دستگاه

با این روش می‌توان میانگین 1010 گرم را ثابت نگه داشت؛ اما در آن صورت ما به 2.5 انحراف معیار که برابر  با 10 گرم  است، نیاز داریم:

10g / 2.5 = 4g

پس انحراف معیار باید برابر با 4 گرم باشد:

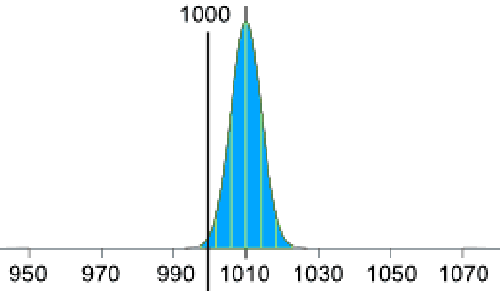
این دقت مطلوبی برای دستگاه بسته‌بندی به نظر می‌رسد.

با کمی تلاش بیشتر می‌توان ترکیبی از دقت بیشتر و میانگین بالاتر به دست آورد.

مقادیر دقیق‌تر
می توان از جدول توزیع نرمال استاندارد استفاده کرد تا مقادیر دقیق تری به دست آورد.