رفتار غیر خطی مواد — به زبان ساده

اکثر سازه‌ها، به منظور عملکرد در محدوده الاستیک خطی (ناحیه پایین‌تر از حد تناسب در منحنی تنش-کرنش) طراحی می‌شوند. به همین دلیل، در بیشتر مسائل مهندسی، موادی مورد بررسی قرار می‌گیرند که رفتار آن‌ها از قانون هوک پیروی می‌کند. در این مقاله، با معرفی منحنی تنش-کرنش غیر خطی، تغییر طول غیر خطی یک میله و کاربرد معادله رامبرگ-ازگود، رفتار مواد پس از حد تناسب (رفتار غیر خطی مواد) را مورد بررسی قرار می‌دهیم. در انتها نیز به تشریح یک مثال کاربردی می‌پردازیم.

منحنی تنش-کرنش غیرخطی

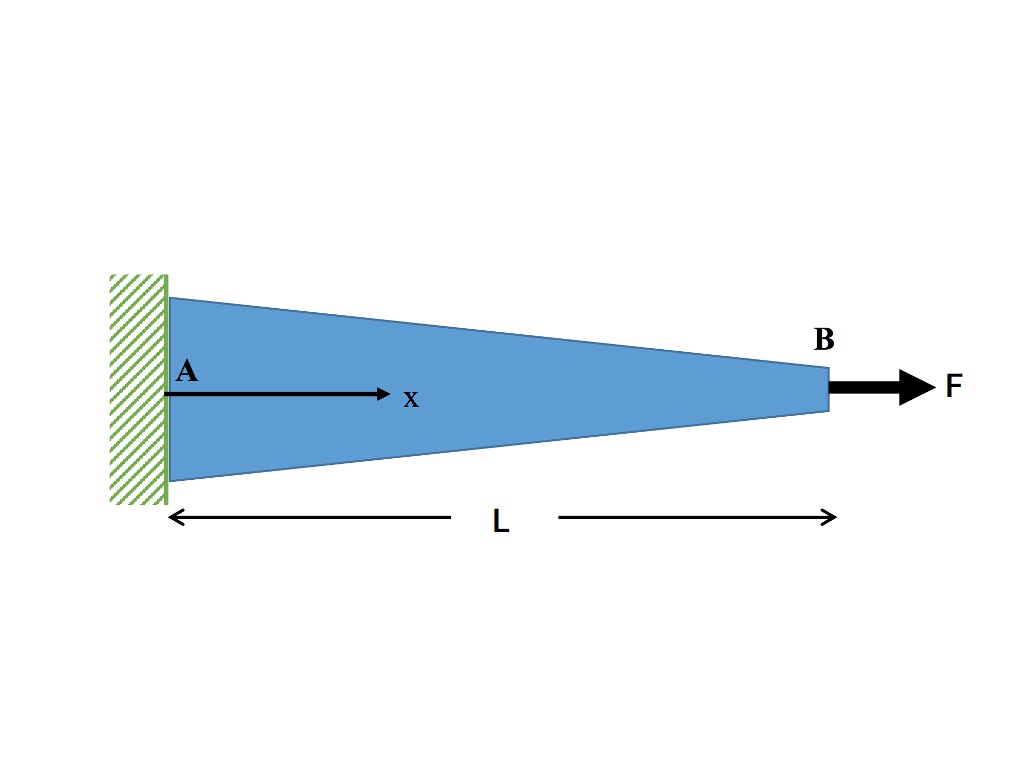
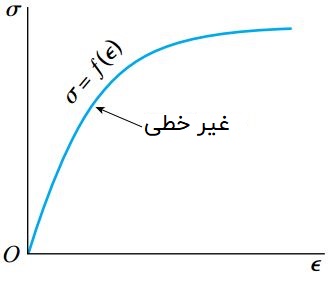
به منظور طراحی و تحلیل رفتار مواد، معمولا منحنی تنش-کرنش واقعی ماده با استفاده از توابع ریاضی به صورت یک منحنی ایده‌آل درمی‌آید. به عنوان مثال، برای شروع منحنی زیر را در نظر بگیرید.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

بخش ابتدایی این منحنی به صورت الاستیک خطی و بخش دوم آن غیر خطی است. هر دو ناحیه مشخص شده در این منحنی توسط روابط ریاضی تعریف شده‌اند.

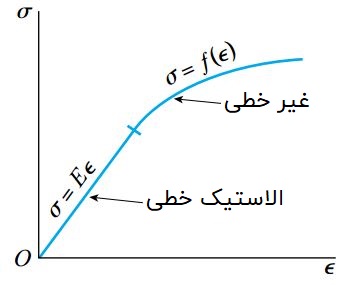
در برخی از موارد می‌توان رفتار دقیق آلیاژهای آلومینیوم تا پیش از رخ دادن کرنش‌های بسیار بزرگ را به وسیله یک منحنی مشابه با مثال بالا نمایش داد.

در شکل زیر، رفتار کلی ماده و تغییرات منحنی تنش-کرنش توسط یک تابع ریاضی نمایش داده شده است. «معادله رامبرگ-ازگود» (Ramberg-Osgood Equation)، یکی از روابط ریاضی شناخته شده برای نمایش این نوع رفتار به شمار می‌رود. در بخش‌های بعدی به معرفی کاربردهای این معادله خواهیم پرداخت.

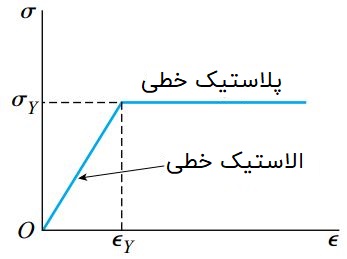
شکل زیر، منحنی تنش-کرنش معمول برای فولاد سازه‌ای را نمایش می‌دهد. منحنی تنش-کرنش فولاد دارای یک ناحیه الاستیک خطی و ناحیه‌ای با سطح تسلیم بسیار بالا است. به همین دلیل، رفتار این ماده را می‌توان توسط دو خط مستقیم نمایش داد. در این مثال فرض می‌شود که تا قبل از رسیدن به تنش تسلیم (σ_y)، ماده از قانون هوک پیروی می‌کند.

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

پس از تنش تسلیم، رفتار ماده با عنوان «پلاستیسیته کامل» (Perfectly Plastic) شناخته می‌شود. ناحیه پلاستیک کامل تا رسیدن میزان کرنش‌ها به 10 یا 20 برابر کرنش تسلیم ادامه می‌یابد. ماده‌ای که رفتار آن مطابق این نوع منحنی باشد، «الاستو پلاستیک» (Elastoplastic) یا «الاستیک-پلاستیک» (Elastic-Plastic) نام دارد.

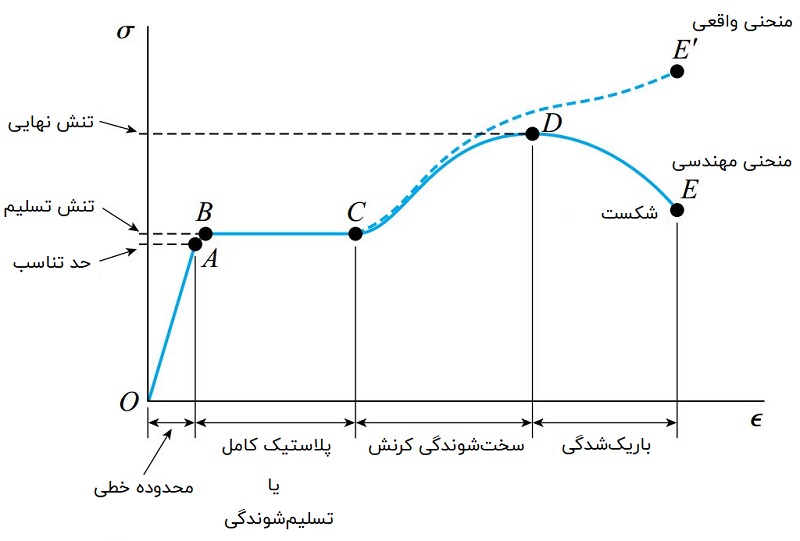
با ایجاد کرنش‌های بسیار بزرگ، شیب منحنی تنش-کرنش فولاد بر اثر سخت‌شوندگی کرنش (Strain Hardening) افزایش می‌یابد (شکل بالا). در لحظه شروع سخت‌شوندگی کرنش، جابجایی‌ها به قدری بزرگ می‌شوند که عملکرد صحیح سازه را با مشکل مواجه می‌کنند. به همین دلیل، رفتار سازه‌های فولادی در هر دو حالت بارگذاری کششی و فشاری معمولاً بر اساس منحنی تنش-کرنش الاستو پلاستیک مورد تحلیل قرار می‌گیرد. به تحلیل‌هایی که بر مبنای این فرضیات انجام می‌شوند، تحلیل الاستو پلاستیک یا تحلیل پلاستیک می‌گویند.

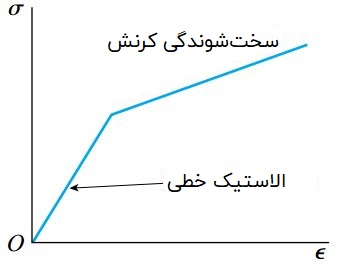
منحنی تنش-کرنش نمایش داده شده در شکل زیر دارای دو خط مستقیم با شیب‌های متفاوت است. به این نوع منحنی، «منحنی تنش-کرنش دوخطی» (Bilinear Stress-Strain Curve) گفته می‌شود. توجه داشته باشید که رابطه بین تنش و کرنش در هر دو بخش به صورت خطی است. با این وجود، میزان تنش فقط در بخش اول با میزان کرنش متناسب است (قانون هوک). این منحنی ایده‌آل را می‌توان برای بیان رفتار موادی با سخت‌شوندگی کرنش یا تخمین منحنی‌های غیر خطی مورد استفاده قرار داد.

تغییر طول میله

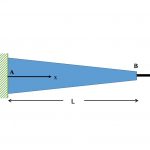
در صورتی که منحنی تنش-کرنش یک ماده مشخص باشد، میزان افزایش یا کاهش طول میله‌ای از جنس آن ماده قابل تعیین خواهد بود. به منظور نمایش فرآیند کلی تعیین تغییر طول یک میله با استفاده از منحنی تنش-کرنش ماده تشکیل‌دهنده آن، شکل زیر را در نظر می‌گیریم. در این شکل، میله مخروطی AB با طول اولیه L نمایش داده شده است.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

مساحت سطح مقطع این میله و همچنین نیروی محوری اعمال شده، در راستای طول تغییر می‌کنند. علاوه بر این، منحنی تنش-کرنش ماده تشکیل‌دهنده میله به صورت غیر خطی است. از آنجایی که میله از نظر استاتیکی معین است، نیروهای محوری داخلی در تمام سطح مقطع‌ها را می‌توان با کمک معادلات تعادل استاتیکی تعیین کرد. میزان تنش‌های موجود نیز از تقسیم این نیروها بر مساحت سطح مقطع‌ها به دست می‌آید. در مرحله بعد، میزان کرنش‌های ایجاد شده با استفاده از منحنی تنش-کرنش تعیین می‌شود. در انتها نیز تغییر طول میله مورد محاسبه قرار می‌گیرد.

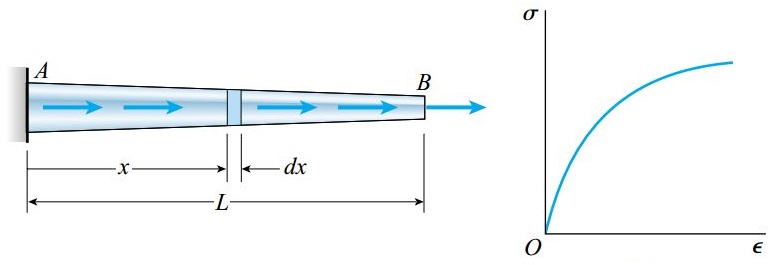
تغییر طول المان dx با کرنش (ε) در فاصله x از انتهای میله برابر است. با انتگرال‌گیری در بازه 0 تا L، میزان تغییر طول کلی میله تعیین می‌شود:

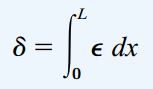
در صورتی که کرنش به صورت تحلیلی و با استفاده از روابط جبری بیان شده باشد، با انتگرال‌گیری از رابطه بالا می‌توان به یک عبارت ریاضی برای محاسبه تغییر طول دست یافت. اگر تنش و کرنش به صورت عددی بیان شده باشند، می‌توان مراحل زیر را به منظور تعیین میزان تغییر طول دنبال کرد:

1. تقسیم میله به بخش‌های کوچکی با طول Δx
2. تعیین میانگین تنش و کرنش در هر یک از بخش‌ها
3. محاسبه تغییر طول در کل میله

این فرآیند معادلِ انتگرال‌گیری از رابطه بالا به وسیله روش‌های عددی است. در صورتی که کرنش درون میله یکنواخت باشد، جواب انتگرال بالا بدیهی خواهد بود. به این ترتیب، تغییر طول میله از رابطه زیر به دست می‌آید:

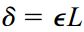
معادله تنش-کرنش رامبرگ-ازگود

در برخی از فلزات نظیر آلومینیوم و منیزیم، منحنی تنش-کرنش ماده با استفاده از معادله رامبرگ-ازگود قابل ترسیم است:

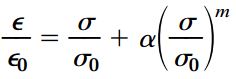
در این معادله، σ و ε به ترتیب تنش و کرنش را نمایش می‌دهد. ε₀ ، σ₀ ، α و m نیز ثابت‌های ماده هستند که از آزمایش‌های کششی به دست می‌آیند. فرم دیگری از این معادله به صورت زیر نوشته می‌شود:

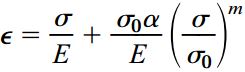
E: مدول الاستیسیته در بخش اولیه منحنی تنش-کرنش است که مقدار آن از رابطه σ₀/ε₀ محاسبه می‌شود.

فیلم آموزش مقاومت مصالح در فرادرس

کلیک کنید

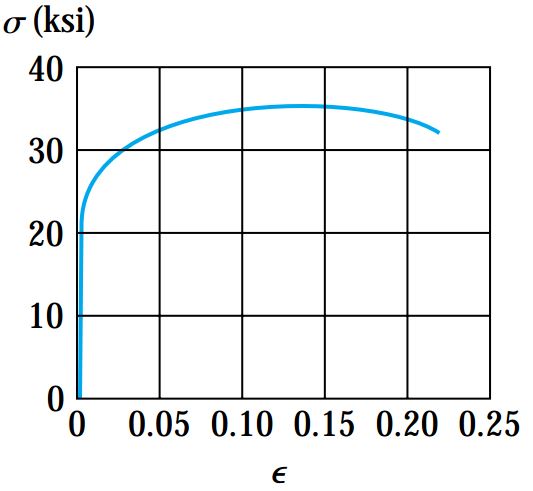
شکل زیر، منحنی تنش-کرنش برای یک نوع آلیاژ آلومینیوم را نمایش می‌دهد. مقادیر مدول الاستیسیته و دیگر ثابت‌های این آلیاژ برابر است با:

E=10*10⁶ psi, σ₀=38000 psi, α=3/7, m=10

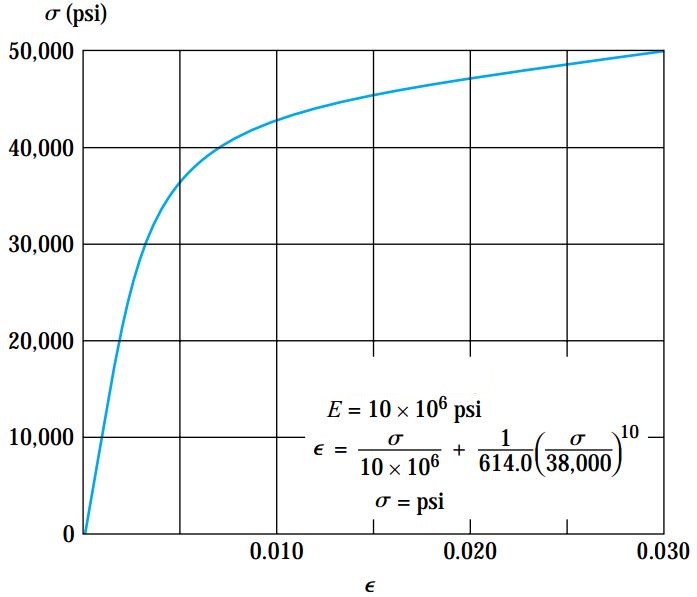
معادله رامبرگ-ازگود برای این منحنی بخصوص به صورت زیر نوشته می‌شود:

واحد تنش در رابطه بالا، پوند بر اینچ مربع (psi) است.

یک آلیاژ آلومینیوم با مشخصات زیر را در نظر بگیرید:

E=70 GPa, σ₀=260 MPa, α=3/7, m=10

معادله رامبرگ-ازگود برای این ماده در سیستم SI به صورت زیر نوشته می‌شود:

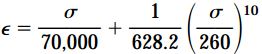
واحد تنش در رابطه بالا، مگا پاسکال (MPa) است.

حل یک مثال کاربردی

میله منشوری AB با طول 2.2 متر و مساحت سطح مقطع 450 میلی‌متر مربع را در نظر بگیرید. این میله مطابق شکل زیر در معرض دو نیروی متمرکز P₁=108kN و P₂=27kN قرار دارد.

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

جنس این میله از یک نوع آلیاژ آلومینیوم با منحنی تنش-کرنش غیر خطی است.

میله‌ای از جنس یک ماده غیر خطی

منحنی تنش-کرنش این میله توسط معادله رامبرگ-ازگود به دست می‌آید:

با توجه به اطلاعات مسئله، جابجایی δ_B در انتهای پایینی میله تحت شرایط زیر را را محاسبه کنید.

• الف) اعمال بار P₁
• ب) اعمال بار P₂
• ج) اعمال هم‌زمان بار P₁ و P₂

الف) جابجایی ناشی از اعمال P₁

بار P₁ باعث ایجاد یک تنش کششی یکنواخت در طول میله می‌شود. این تنش از طریق رابطه P₁/A به دست می‌آید و مقدار آن برابر با 225MPa است. با جایگذاری این مقدار در رابطه تنش-کرنش، میزان کرنش برابر با ε=0.003589 می‌شود. به این ترتیب، تغییر طول میله (جابجایی آن در نقطه B) از طریق رابطه زیر به دست می‌آید:

ب) جابجایی ناشی از اعمال بار P₂

تنش موجود در نیمه بالایی میله برابر با P₂/A یا 56.25MPa است. در این حالت، هیچ تنش در نیمه پایینی میله وجود ندارد. همانند بخش الفِ این مثال، تغییر طول میله از طریق رابطه زیر محاسبه می‌شود:

ج) جابجایی ناشی از اعمال هم‌زمان بار P₁ و P₂

میزان تنش موجود در نیمه پایینی میله از طریق رابطه P1/A و تنش موجود در نیمه بالایی آن از طریق رابطه P₁+P₂/A به دست می‌آید. مقدار هر از این تنش‌ها به ترتیب برابر 225MPa و 281.25MPa است. به این ترتیب، مقادیر کرنش‌های حاصل از این تنش‌ها به ترتیب برابر 0.003589 و 0.007510 خواهد بود (بر اساس معادله رامبرگ-ازگود). در نتیجه، تغییر طول میله به صورت زیر تعیین می‌شود:

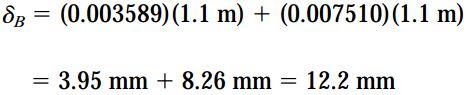
نتیجه‌گیری

مقایسه مقادیر به دست آمده برای δ_B در بخش‌های مختلف مسئله، یکی از اصول مهم مربوط به سازه‌های متشکل از مواد غیر خطی را نمایش می‌دهد. بر اساس این اصل، جابجایی ناشی از اعمال هم‌زمان دو یا چند بار در یک سازه غیر خطی با حاصل جمع جابجایی‌های ناشی از اعمال جداگانه هر بار برابر نیست.

^^