تئوری مور-کولمب — آشنایی با خصوصیات رفتاری مواد

«تئوری مور-کولمب» (Mohr–Coulomb Theory)، یک مدل ریاضی برای توصیف عکس‌العمل مواد شکننده‌ای مانند بتن در برابر تنش‌های نرمال و برشی است. در اکثر مواد کلاسیک مهندسی، بخشی از پوش شکست برشی به نحوی از این تئوری پیروی می‌کند. به طور کلی، تئوری مور-کولمب برای موادی به کار می‌رود که مقاومت فشاری آن‌ها بسیار بیشتر از مقاومت کششی باشد.

در مهندسی ژئوتکنیک، از تئوری مور-کولمب برای مشخص کردن مقاومت برشی خاک و سنگ در سطوح مختلف تنش مؤثر و در مهندسی سازه، از این تئوری برای تعیین بار و زاویه شکست در بتن و مواد مشابه استفاده می‌شود. علاوه بر این، فرضیه اصطکاک کولمب نیز جهت به دست آوردن ترکیب تنش نرمال و برشی به وجود آورنده شکست کاربرد دارد. «دایره مور» (Mohr’s Circle)، تنش‌های اصلی ایجاد کننده این ترکیب و زاویه صفحه اعمال آن‌ها را تعیین می‌کند.

اگر شکست یک ماده بر اساس فرضیه اصطکاک کولمب رخ دهد، زاویه خط جابجایی موجود در محل شکست با زاویه اصطکاک برابر خواهد بود. با توجه به این ویژگی می‌توان با مقایسه کار مکانیکی خارجی حاصل از جابجایی و بارگذاری خارجی و همچنین کار مکانیکی داخلی حاصل از تنش و کرنش در خط شکست، مقاومت ماده را محاسبه کرد. بر اساس اصل پایستگی انرژی، مجموع این مقادیر باید صفر باشد. این موضوع، امکان محاسبه بارگذاری شکست سازه را فراهم می‌کند. یکی از پیشرفت‌های مدل مور-کولمب، توصیف شکستگی جدا شده توسط ترکیب قانون اصطکاک کولمب با «قاعده رانکین» (Rankine's Principal) است.

تاریخچه توسعه تئوری مور-کولمب

تئوری مور-کولمب توسط «شارل آگوستن دو کولُن» (Charles-Augustin de Coulomb) و «کریستین اتو مور» (Christian Otto Mohr) توسعه داده شده است. کولن (کولمب) در سال 1773 مقاله‌ای را در زمینه بررسی کاربرد قوانین حداکثری و حداقلی برای حل برخی از مسائل استاتیک در حوزه معماری تألیف کرد.

فیلم آموزش مکانیک خاک – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

مور نیز در اواخر قرن 19 ام میلادی، فرم تعمیم‌یافته‌ای از تئوری کولمب را ارائه کرد. این فرم تعمیم‌یافته، تنها نحوه تفسیر معیار ارائه شده را تحت تأثیر قرار داد و در ذات آن تغییری ایجاد نکرد. از این‌رو، در برخی از منابع، این فرم هنوز هم با عنوان «معیار کولمب» (Coulomb Criterion) شناخته می‌شود.

معیار شکست مور-کولمب

«معیار شکست مور-کولمب» (Mohr–Coulomb Failure Criterion)، پوش خطی حاصل از نمودار مقاومت برشی ماده در مقابل تنش نرمال اعمال شده به آن را نشان می‌دهد. رابطه ریاضی این معیار به صورت زیر تعریف می‌شود:

$$\tau =\sigma ~\tan(\phi )+c$$

τ: مقاومت برشی؛ σ: تنش نرمال؛ c: تقاطع پوش شکست با محور مقاومت برشی؛ (tan(ϕ: شیب پوش شکست

کمیت c معمولاً با عنوان «چسبندگی» (Cohesion) و ϕ با عنوان «زاویه اصطکاک داخلی» (Internal Friction Angle) شناخته می‌شود. معمولاً علامت تنش در هنگام اعمال فشار، مثبت (+) در نظر گرفته می‌شود. در صورت فرض منفی بودن علامت فشار، باید σ– را جایگزین σ کرد.

اگر ϕ=0 باشد، معیار مور-کولمب به «معیار ترسکا» (Tresca Criterion) تبدیل می‌شود. در طرف مقابل، اگر ϕ=90 باشد، مدل مور-کولمب با «مدل رانکین» (Rankine Model) برابر خواهد بود. علاوه بر این، زاویه اصطکاک داخلی نمی‌تواند مقداری بیشتر از 90 درجه داشته باشد.

فیلم آموزش مکانیک خاک – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

بر اساس روابط موجود در دایره مور داریم:

$$\sigma =\sigma _{m}-\tau _{m}\sin \phi ~;~~\tau =\tau _{m}\cos \phi$$

که در آن:

$${\displaystyle \tau _{m}={\cfrac {\sigma _{1}-\sigma _{3}}{2}}~;~~\sigma _{m}={\cfrac {\sigma _{1}+\sigma _{3}}{2}}}$$

σ₁: تنش اصلی ماکسیمم؛ σ₃: تنش اصلی مینیمم

بر اساس معادلات بالا می‌توان معیار مور-کولمب را به صورت زیر نیز نوشت:

$$\tau _{m}=\sigma _{m}\sin \phi +c\cos \phi ~$$

این شکل از معیار مور-کولمب برای حالتی مناسب است که سطح شکست با جهت σ₂ موازی باشد.

معیار شکست مور-کولمب در سه بعد

معیار مور-کولمب در مختصات سه‌بعدی اغلب به صورت زیر تعریف می‌شود:

$$\begin{aligned}\pm {\cfrac {\sigma _{1}-\sigma _{2}}{2}}&=\left[{\cfrac {\sigma _{1}+\sigma _{2}}{2}}\right]\sin(\phi )+c\cos(\phi )\\\pm {\cfrac {\sigma _{2}-\sigma _{3}}{2}}&=\left[{\cfrac {\sigma _{2}+\sigma _{3}}{2}}\right]\sin(\phi )+c\cos(\phi )\\\pm {\cfrac {\sigma _{3}-\sigma _{1}}{2}}&=\left[{\cfrac {\sigma _{3}+\sigma _{1}}{2}}\right]\sin(\phi )+c\cos(\phi )\end{aligned}$$

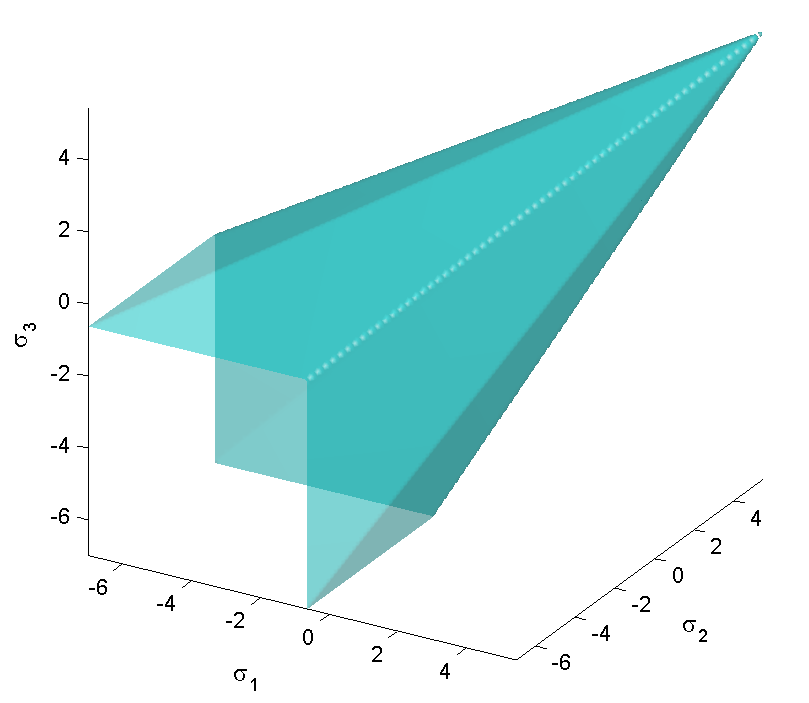
سطح شکست مور-کولمب مخروطی با مقطع شش‌وجهی در دستگاه مختصات تنش انحرافی است.

با بسط دادن تنش‌های نرمال و تنش برشی به دست آمده در یک صفحه با جهت‌گیری دلخواه نسبت به محورهای مختصات (بردارهای پایه)، می‌توان عبارات  τ و σ را در سه بعد تعمیم داد. فرض کنید که بردار یکه نرمال برای صفحه مورد نظر به صورت زیر باشد:

$${\mathbf {n}}=n_{1}~{\mathbf {e}}_{1}+n_{2}~{\mathbf {e}}_{2}+n_{3}~{\mathbf {e}}_{3}$$

در معادله بالا، e_i بردار یکه پایه در جهت i=1,2,3 (سه بردار عمود بر هم) را نشان می‌دهد. اگر تنش‌های اصلی σ₂، σ₁ و σ₃ با بردارهای e₂، e₁ و e₃ هم‌راستا باشند، عبارات τ و σ به صورت زیر به دست خواهند آمد:

$${\displaystyle {\begin{aligned}\sigma &=n_{1}^{2}\sigma _{1}+n_{2}^{2}\sigma _{2}+n_{3}^{2}\sigma _{3}\\\tau &={\sqrt {(n_{1}\sigma _{1})^{2}+(n_{2}\sigma _{2})^{2}+(n_{3}\sigma _{3})^{2}-\sigma ^{2}}}\\&={\sqrt {n_{1}^{2}n_{2}^{2}(\sigma _{1}-\sigma _{2})^{2}+n_{2}^{2}n_{3}^{2}(\sigma _{2}-\sigma _{3})^{2}+n_{3}^{2}n_{1}^{2}(\sigma _{3}-\sigma _{1})^{2}}}\end{aligned}}}$$

با تعیین مقادیر معادلات بالا، معیار مور-کولمب توسط رابطه اصلی زیر برای شش صفحه معرف تنش برشی ماکسیمم به دست می‌آید:

$$\tau =\sigma ~\tan(\phi )+c$$

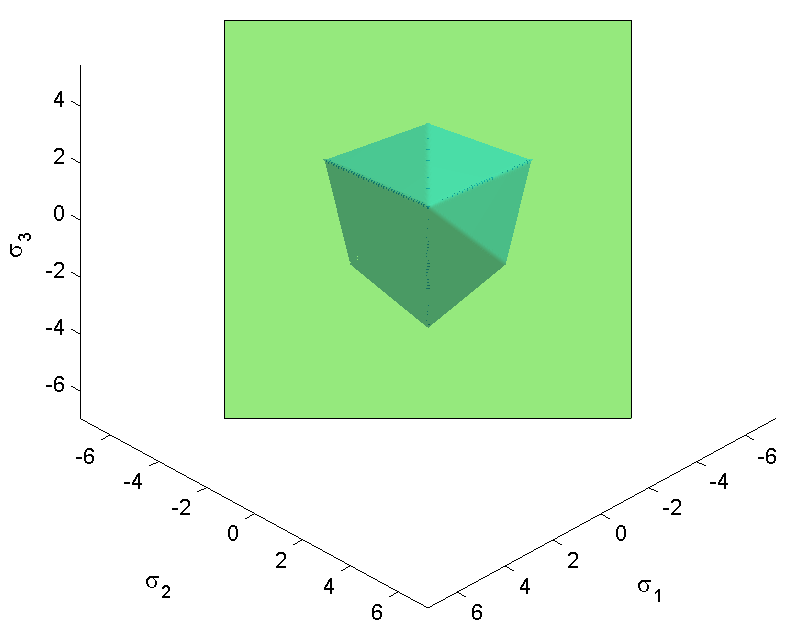
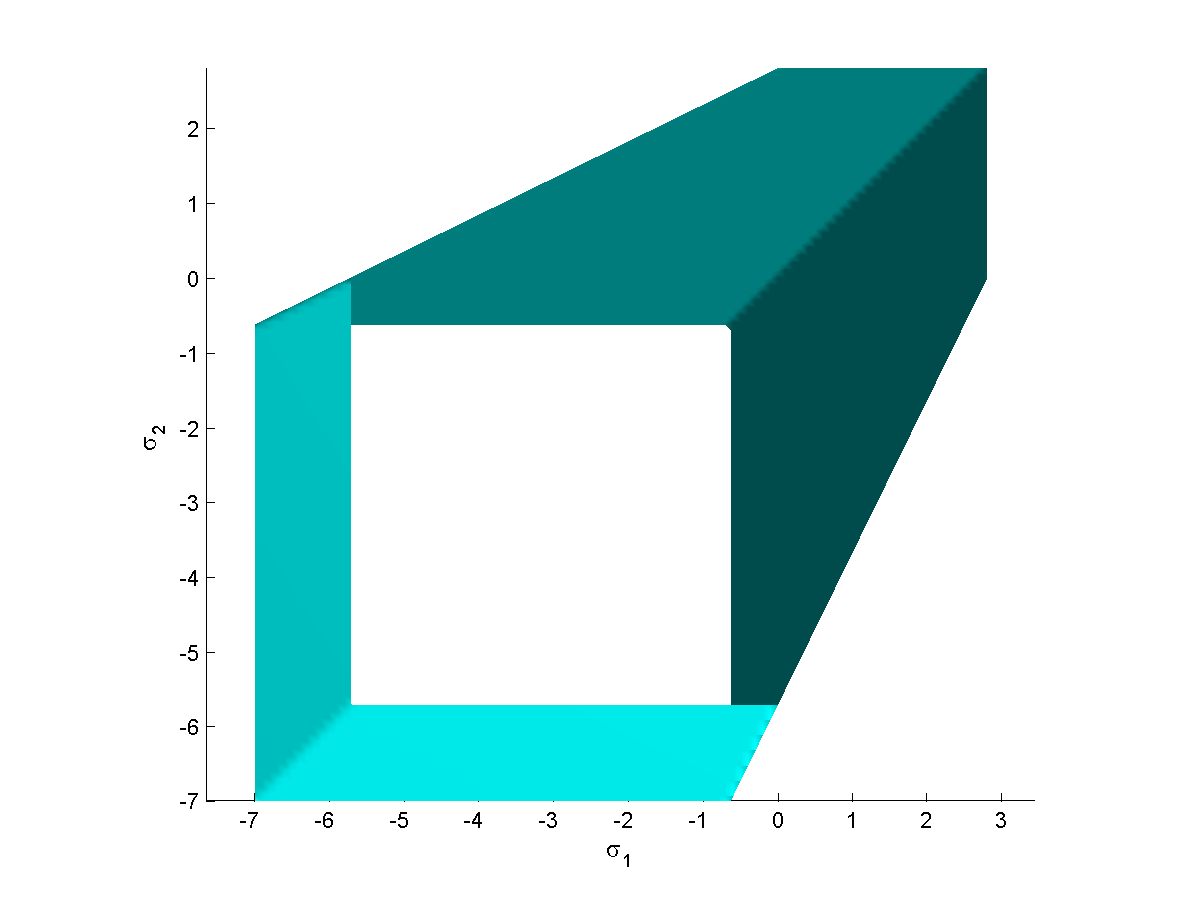
سطح شکست مور-کولمب در مختصات های-وسترگارد

سطح (تسلیم) شکست مور-کولمب، اغلب در دستگاه مختصات «های-وسترگارد» (Haigh–Westergaard) بیان می‌شود (یک نوع دستگاه مختصات استوانه‌ای).

فیلم آموزش مکانیک خاک – مرور و حل مساله در فرادرس

کلیک کنید

به عنوان مثال، تابع زیر را در نظر بگیرید:

$${\displaystyle {\cfrac {\sigma _{1}-\sigma _{3}}{2}}={\cfrac {\sigma _{1}+\sigma _{3}}{2}}~\sin \phi +c\cos \phi }$$

این تابع را می‌توان به صورت زیر نیز نوشت:

$$\left[{\sqrt {3}}~\sin \left(\theta +{\cfrac {\pi }{3}}\right)-\sin \phi \cos \left(\theta +{\cfrac {\pi }{3}}\right)\right]\rho -{\sqrt {2}}\sin(\phi )\xi ={\sqrt {6}}c\cos \phi$$

با در نظر گرفتن کمیت‌های تغییرناپذیر q، p و r، معادله بالا به شکل زیر تبدیل خواهد شد:

$$\left[{\cfrac {1}{{\sqrt {3}}~\cos \phi }}~\sin \left(\theta +{\cfrac {\pi }{3}}\right)-{\cfrac {1}{3}}\tan \phi ~\cos \left(\theta +{\cfrac {\pi }{3}}\right)\right]q-p~\tan \phi =c$$