همنهشتی – به زبان ساده

نظریه همنهشتی یا حساب پیمانه‌ای یکی از شاخه‌های مهم نظریه اعداد است که مبدع آن کارل فردریش گاوس است. گرچه این شاخه از نظریه اعداد عموماً توجه چندانی را برنمی‌انگیزد، اما در واقع ابزار بسیار قدرتمندی برای محاسبات مختلف است. در واقع بهتر است که همه ما در کنار عملیات جمع و ضرب معمولی با این روش محاسبه مبتنی بر باقی‌مانده تقسیم نیز آشنایی داشته باشیم.

در این راهنما به جای این که مانند اغلب نوشته‌های دیگر شما را زیر بمباران فرمول‌ها قرار دهیم، تلاش خواهیم کرد تا درکی شهودی از مفهوم همنهشتی در ذهن شما ایجاد کنیم و آن را به زبانی کاملاً ساده توضیح دهیم.

اعداد زوج، فرد و مضارب 3

وقتی که نخستین بار در دبستان با اعداد آشنا شدیم، بی‌درنگ مفهومی به نام زوج یا فرد بودن را ما آموزش داده‌اند:

• اعداد زوج: اعدای هستند که بر 2 بخش‌پذیر هستند (0، 2، 4، 6، ...)
• اعداد فرد: اعدادی هستند که بر 2 بخش‌پذیر نیستند (1، 3، 5، 7، ...)

اما سؤال این است که این تمایز چرا مهم است؟ چون در واقع این آغاز تفکر انتزاعی (مجرد) است. ما در این زمان شروع به تفکر در مورد خصوصیات عدد (زوج و فرد بودن) می‌کنیم و از اندیشه صرف در مورد خود عدد (مثلاً 37) فراتر می‌رویم.

این تفکر انتزاعی گامی بزرگ است، چون به ما امکان می‌دهد که ریاضیات را در سطحی عمیق‌تر کاوش کنیم و روابط بین اعداد را درک نماییم. برای نمونه می‌توانیم قواعدی مانند زیر بسازیم:

• عدد زوج × عدد زوج = عدد زوج
• عدد فرد × عدد فرد = عدد فرد
• عدد زوج × عدد فرد = عدد زوج

تفکر شهودی

این‌ها قواعدی کلی هستند و در سطح همه خصوصیات اعداد عمل می‌کنند. اگر بخواهیم شهودی‌تر فکر کنیم می‌توانیم قیاسی از شیمی بیاوریم که زوج بودن یک عدد، مولکولی است که برخی اعداد (مواد) دارند و با ضرب کردن (فرایند شیمیایی) نمی‌توان این خصوصیت را از آن‌ها گرفت. اما زوج/فرد بودن یک خصوصیت کاملاً مشخص است: تقسیم بر 2. اینک در مورد عدد 3 چه می‌توانیم بگوییم؟

• همه مضارب 3 بر عدد 3 بخش‌پذیر هستند (0، 3، 6، 9، ...)
• اعداد غیر مضرب 3 بر عدد 3 بخش‌پذیر نیستند (1، 2، 4، 5، 7، 8، ...)

گرچه عجیب است، اما واقعیت دارد. در این جا چند نکته را متوجه می‌شویم: دو نوع عدد غیر مضرب 3 وجود دارند. اعدادی مانند 4 که 1 واحد از مضارب 3 بزرگ‌تر هستند (باقی‌مانده 1 هنگام تقسیم بر 3) و اعدادی مانند 5 که دو واحد بزرگ‌تر هستند (یعنی باقی‌مانده تقسیم آن‌ها بر 3 برابر با 2 است)

مضرب 3 بودن نیز یک خصوصیت دیگر هر عددی است. البته شاید به اندازه زوج/فرد بودن کارایی نداشته باشد؛ اما به هر حال چنین خصوصیتی وجود دارد و می‌توانیم قواعدی مانند زیر بسازیم:

• مضرب 3 × مضرب 3 = مضرب 3
• و ...

اما این وضعیت را تا کجا می‌توانیم ادامه بدهیم؟

به همنهشتی خوش آمدید

عملیات پیمانه‌ای (با عبارت اختصاری mod یا % در اغلب زبان‌های برنامه‌نویسی) مقدار باقی‌مانده حاصل از تقسیم بر یک عدد را ارائه‌ی کند. برای مثال

5 mod 3 = 2

یعنی 2 باقی‌مانده تقسیم 5 بر 3 است.

فیلم آموزش ریاضیات گسسته پایه دوازدهم – مرور و حل مساله در فرادرس

کلیک کنید

اگر بخواهیم واژه‌های روزمره را به زبان ریاضیات تبدیل کنیم، باید بگوییم که یک عدد زوج عددی است که خصوصیت «0 mod 2» دارد یعنی باقی‌مانده آن هنگامی که بر 2 تقسیم می‌شود، برابر با صفر است. عدد فرد به صورت «1 mod 2» است یعنی باقیمانده ش 1 است.

اما دلیل این نوع نگارش چیست؟ وقتی بخواهیم قواعد «زوج/فرد» که قبلاً بیان کردیم را به زبان ریاضیات بنویسیم:

• زوج × زوج = 0 × 0 = 0 [زوج]
• فرد × فرد= 10 × 1 = 1 [فرد]
• زوج × فرد = 1 × 0 = 0 [زوج]

می‌بینید که این روش محاسبه چقدر آسان‌تر است. در واقع می‌توانید ببینید که یک عدد زوج در هر عددی ضرب شود، حاصل‌ضرب آن عددی زوج خواهد بود، یعنی باقیمانده برابر با صفر است.

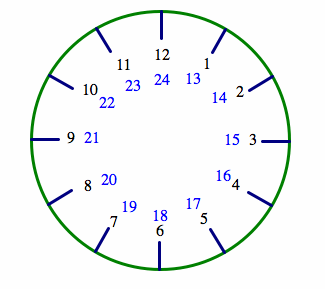
ریاضیات روی عقربه‌های ساعت

نکته جالب در مورد همنهشتی آن است که ما همواره در مورد محاسبات مربوط به ساعت از آن استفاده می‌کنیم. برای مثال فرض کنید ساعت 07:00 است (مهم نیست که قبل یا بعد از ظهر باشد). اینک سؤال این است که عقربه ساعت شما 7 ساعت بعد روی چه عددی خواهد بود؟

پاسخ این است که 14 = 7+7؛ اما ما می‌دانیم که روی صفحه هیچ ساعتی عدد 14:00 وجود ندارد. بنابراین ساعت باید 2 باشد. این استدلال به صورت شهودی انجام می‌یابد و اگر بخواهیم به زبان ریاضیاتی پاسخ دهیم باید بگوییم که

(7 + 7) mod 12 = (14) mod 12 = 2 mod 12 (یعنی 2 باقیمانده تقسیم 14 بر 12 است)

معادله زیر

14 mod 12 = 2 mod 12

به این معنی است که در یک ساعت با صفحه‌ای که به دوازده بخش تقسیم شده، ساعت‌های 2 و 14 شبیه هم هستند. در واقع می‌گوییم این دو متجانس هستند و با علامت سه خط موازی رو هم نشان داده می‌شود:

14 ≡ 2 mod 12

مثال دیگر به صورت زیر است: فرض کنید ساعت اینک 08:00 باشد، 25 ساعت دیگر عقربه ساعت شما روی کدام است؟

در این موقعیت به جای این که 25 واحد به 8 اضافه کنیم، می‌توانیم با کمی تأمل متوجه شویم که 25 ساعت همان «1 شبانه‌روز + 1 ساعت» است. 25 ساعت دیگر، عقربه ساعت شمار تنها 1 واحد جلوتر خواهد بود، یعنی روی ساعت 09:00.

(8 + 25) mod 12 ≡ (8) mod 12 + (25) mod 12 ≡ (8) mod 12 + (1) mod 12 ≡ 9 mod 12

بدین ترتیب به صورت شهودی ساعت 25 را به ساعت 1 تبدیل کرده و به ساعت 8 اضافه کردیم. ما با استفاده از ساعت به عنوان یک مقایسه می‌توانیم درک کنیم که قواعد همنهشتی چگونه عمل می‌کنند.

جمع/تفریق

فرض کنیم دو زمان هستند که روی عقربه‌های ساعت مشابه هم هستند (مثلاً: ساعت 02:00 و ساعت 14:00) اگر مقدار x را به هر دو ساعت اضافه کنیم، چه رخ می‌دهد؟ بدیهی است که این دو زمان مجدداً هر دو به زمان یکسانی روی ساعت اشاره می‌کنند یعنی:

2:00 + 5 ساعت≡ 14:00 + 5 ساعت

هر دو این مقادیر به ساعت 07:00 اشاره خواهند کرد. واقعیت این است که ما در چنین مواردی هرگز وقتی عقربه از ساعت 12 بگذرد مقدار 14 ساعت را در نظر نمی‌گیریم و باقیمانده تقسیم عدد بر 12 یعنی 2 را در نظر می‌گیریم و می‌دانیم که هر دو آن‌ها به یک میزان پیشروی می‌کنند. برای همه اعداد متجانس (2 و 14) جمع یا تفریق نتیجه یکسانی ارائه می‌کنند.

ضرب

مشاهده وضعیت ضرب در چنین مواردی کمی دشوارتر است. اگر

14 ≡ 2 (mod 12)

باشد، در این صورت آیا می‌توانیم هر دو طرف را در عدد واحدی ضرب کرده و نتیجه یکسانی بگیریم؟ در ادامه بررسی می‌کنیم که وقتی دو طرف عبارت فوق در 3 ضرب شود چه اتفاقی رخ می‌دهد؟

می‌دانیم که 2:00 * 3 ≡ 6:00 است؛ اما در مورد 14:00 * 3 چه می‌توان گفت؟ به خاطر داشته باشید که 14 = 12 + 2 بنابراین می‌توان گفت:

14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12

بخش اول یعنی 12 * 3 را می‌توانید نادیده بگیرید. بخش 12 ساعت همان برابر با صفر است و ساعت 14 چند بار آن را در خود دارد. ولی این مقدار اهمیتی ندارد و در هر صورت آن را نادیده می‌گیریم.

هنگامی که می‌خواهیم ضرب کنیم تنها باقی‌مانده است که اهمیت دارد که برای 14:00 و 02:00، همان 2 ساعت است. به طور شهودی می‌بینیم که ضرب، تغییری در محاسبات همنهشتی ایجاد نکرده است، یعنی دو طرف همنهشتی در عدد یکسانی ضرب شده و نتیجه یکسانی حاصل آمده است.

استفاده از حساب پیمانه‌ای

سؤالی که اینک پیش می‌آید این است که حساب پیمانه‌ای چه فایده‌ای دارد؟

محاسبات ساده زمانی

ما از این محاسبات به صورت شهودی استفاده می‌کنیم؛ اما چه بهتر که نامی برای آن داشته باشیم. فرض کنید پرواز شما ساعت 3 بعد از ظهر می‌رسد. اگر این پرواز 14 ساعت پرواز تأخیر داشته باشد، پرواز چه ساعتی بر زمان خواهد نشست؟

می‌دانیم که

14 ≡ 2 mod 12

بنابراین می‌توانیم این طور فرض کنیم که «14 ساعت برابر است با 2 ساعت به علاوه تغییر قبل/بعد از ظهر». بنابراین می‌دانیم که ساعت نشستن هواپیما به صورت 3 + 2 = 5 قبل از ظهر خواهد بود. محاسباتی که در ادامه ارائه کرده‌ایم، کمی پیچیده‌تر از عملگر پیمانه‌ای ساده است؛ اما مفهوم آن یکسان است.

قرار دادن آیتم‌ها در گروه‌های تصادفی

فرض کنید افرادی هستند که بلیت‌های سینما را به وسیله یک شماره تأیید خریداری کرده‌اند. شما می‌خواهید این افراد را به دو دسته تقسیم کنید.

چه باید کرد؟ «شماره‌های فرد این طرف و شماره‌های زوج طرف دیگر». لزومی ندارد که بدانید چه تعداد بلیت صادر شده است. بدین ترتیب هر کس می‌تواند گروه خود را بدون نیاز به ارتباط با یک مرجعیت مرکزی بی‌درنگ بداند و این طرح با افزایش تعداد خریداران بلیت همچنان پاسخگو است.

اگر به 3 گروه نیاز داشته باشیم چطور؟ در این حالت باید شماره تأیید را بر 3 تقسیم کنید و باقی‌مانده را در نظر بگیرید (یعنی mod 3) در این صورت گروه‌هایی به صورت 0، 1 و 2 داریم.

در برنامه‌نویسی از عملگر پیمانه برای قرار دادن آیتم‌ها در یک جدول هش استفاده می‌شود. اگر جدول ما N مدخل داشته باشد، در این صورت کلید آیتم را به یک عدد تبدیل می‌کنیم، باقی‌مانده آن را بر N (mod N) به دست می‌آوریم و آیتم را در گروهی که مربوط است قرار می‌دهیم. در این موارد احتمالاً از یک لیست پیوندی برای نگهداری آیتم‌ها استفاده می‌شود. با افزایش اندازه جدول هش، می‌توانید پیمانه را برای کلیدها مجدداً محاسبه کنید.

انتخاب یک آیتم به صورت تصادفی

ما در زندگی روزمره خود نیز از همنهشتی استفاده می‌کنیم. فرض کنید 4 نفر داریم که به یک بازی مشغول هستند و باید یک نفر به عنوان اولین بازیکن انتخاب شود. در این وضعیت می‌توانیم یک بازی کوچک به صورت «باقی‌مانده 4» داشته باشیم. به هر یک از افراد به ترتیب یکی از اعداد 1، 2، 3 و 4 می‌دهیم. سپس با شمارش از یک تا 4 هر کس به طور همزمان یک عدد تصادفی اعلام می‌کند. همه اعداد را با هم جمع می‌کنیم و بر 4 تقسیم می‌کنیم. هر کس که باقیمانده محاسبه شده را داشته باشد، بازیکن اول خواهد بود. برای مثال فرض کنید مجموع اعداد 11 باشد، هر کس که باقیمانده 3 را داشته باشد، بازیکن اول خواهد بود، زیرا 11 mod 4 = 3. این یک روش ساده و آسان است.

اجرای دوره‌ای یک سری وظایف

فرض کنید نیاز داریم کارهای زیر را دریک زمان‌بندی معین انجام دهیم:

• وظیفه الف هر ساعت سه بار صورت می‌گیرد.
• وظیفه ب هر ساعت 6 بار انجام می‌یابد.
• وظیفه ج هر ساعت 1 بار صورت می‌پذیرد.

این اطلاعات را چگونه می‌توانیم ذخیره کرده و یک جدول زمان‌بندی ایجاد کنیم؟ یکی از روش‌ها چنین است:

• یک تایمر داشته باشیم که هر دقیقه یک بار عمل می‌کند (شماره دقیقه‌ها را به صورت یک متغیر n ردگیری می‌کند)
  منظور از هر ساعت 3 بار یعنی هر 60/3 = 20 دقیقه یک بار. بنابراین وظیفه الف هر زمان که «n% 20 == 0» باشد انجام می‌یابد.
• وظیفه ب هر زمان که «n% 10 == 0» انجام می‌یابد.
• وظیفه ج هر زمان که «n% 60 == 0» انجام می‌یابد.

حال فرض کنید وظیفه ج 1 را داریم که 1 بار در هر ساعت اجرا می‌شود؛ اما همان وظیفه ج نیست. مطمئناً این وظیفه نیز باید زمانی که «n mod 60 == 1» است اجرا شود. یعنی گرچه هر ساعت یک بار اجرا می‌شود؛ اما وظیفه ج نیست.

به طور ذهنی یک دایره می‌بینیم که در بازه‌های مختلف باید کار معینی صورت بگیرد. بنابراین از همنهشتی استفاده می‌کنیم. نکته جالب این است که این کارها در بازه‌های مختلف می‌توانند مستقل از هم باشند و همچنان همپوشانی نیز داشته باشند. این وضعیت تا حدودی شبیه عملگر XOR است که در آن هر XOR می‌تواند در لایه مجزایی باشد، اما توضیح این وضعیت خارج از حوصله این مقاله است.

به طور مشابه وقتی برنامه‌نویسی می‌کنیم، می‌توانیم از هر 100 آیتم گزارش شده یکی را با دستور زیر نمایش دهیم:

if (n% 100 == 0){ print… }

این یک روش بسیار ساده و انعطاف‌پذیر برای اجرای وظایف مختلف در زمان‌بندی مشخص است. در واقع در موارد مختلف اگر از عملیات همنهشتی بهره بگیرید، پاسخ دادن به اغلب مسائل بسیار آسان‌تر خواهد بود.

یافتن مشخصات اعداد

فرض کنید حالت زیر برقرار باشد:

a = (47 * 2 * 3)

فیلم آموزش ریاضیات گسسته – جامع و به زبان ساده در فرادرس

کلیک کنید

در اولین نگاه چه نتیجه‌ای استنتاج می‌شود؟ می‌دانیم که a باید زوج باشد، چون با چیزی برابر است که شامل ضرب در 2 است. اگر به شما گفته شود که

a = (39 * 7)

احتمالاً شگفت‌زده می‌شوید، نه به این خاطر که می‌دانید دو حاصل‌ضرب متفاوت هستند، بلکه چون یکی به وضوح فرد و دیگری زوج است. پس مشکلی وجود دارد، a نمی‌تواند عدد یکسانی در هر دو مورد باشد، زیرا مشخصات این دو عدد با هم مطابقت ندارند.

بررسی صحت معادلات

چیزهایی مانند زوج، مضرب 3 و mod n مشخصاتی هستند که عمومی‌تر از اعداد منفرد هستند و می‌تواند خصوصیتی برای بررسی یکپارچگی باشد. بنابراین می‌توانیم از عملگر پیمانه برای درک این که اعداد با هم مطابقت دارند یا نه استفاده کنیم و همچنان خود عدد را ندانیم!

اگر به شما گفته شود که

3a + 5b = 8

3a + b = 2

آیا معادله‌های فوق با اعداد صحیح قابل حل هستند؟ ببینیم:

3a + 5b = 8 → 0 + 2b ≡ 2 mod 3, یا b ≡ 1 mod 3

3a + b = 2 → 0 + b ≡ 2 mod 3, یا b ≡ 2 mod 3

می‌بینیم که تناقضی وجود دارد:

1 mod 3

2 mod 3

و می‌بینیم که امکان زوج و فرد بودن به طور همزمان وجود ندارد.

اما یک نکته وجود دارد. اعدادی مانند 1.5 نه زوج هستند و نه فرد. چون این اعداد، عدد صحیح نیستند. خصوصیت پیمانه‌ای در مورد اعداد صحیح کاربرد دارد و از این رو می‌توانیم بگوییم که عدد b نمی‌تواند یک عدد صحیح باشد.

در ادامه معادلات را عملاً حل می‌کنیم:

(3a + 5b) – (3a +b) = 8 – 2

4b = 6

b = 1.5

3a + 1.5 = 2

3a = 0.5

a = 1/6

بنابراین نباید مقهور قدرت همنهشتی بشوید و باید محدودیت‌های آن را نیز بپذیریم. عملیات‌های همنهشتی تنها روی اعداد صحیح کاربرد دارند.

رمزنگاری

یکی از مهم‌ترین جنبه‌های رمزنگاری کار با اعداد است. گرچه توضیحش خارج از حیطه این مقاله است، اما از پیمانه‌ها در مبادله کلید دیف-هیلمن (Diffie-Hellman) استفاده می‌شود. این روش رمزنگاری در پروتکل SSL برای مبادله ترافیک‌های وب‌سایت مورد استفاده قرار می‌گیرد.

همنهشتی به بیان ساده

برخی افراد به استفاده از واژه‌ها در چارچوب‌های منظم علاقه‌مند هستند. ممکن است شنیده باشید که «X همان Y به پیمانه Z است.» که معنی تقریبی آن چنین است: «اگر Z را نادیده بگیریم، X و Y یکسان هستند.» برای نمونه:

• B و b به پیمانه حروف بزرگ یکسان هستند.
• iTouch و iPad به پیمانه اندازه، یکسان هستند.

سخن پایانی

تفکر در مورد کاربردهای عملیات همنهشتی چیز عجیبی است. مانند این است که کسی در مورد فایده توان بپرسد. در زندگی روزمره می‌توان در موارد زیادی از همنهشتی به عنوان ابزاری برای درک الگوها در دنیا و ایجاد الگوهای خاص استفاده کرد.

به طور کلی، چندین کاربرد عمومی محاسبات همنهشتی را در ادامه فهرست کرده‌ایم:

• کاهش محدوده: یک ورودی را در نظر بگیرید، آن را به پیمانه N حساب کنید و بدین ترتیب اعدادی از 0 تا N-1 دارید.
• انتساب به گروه: یک ورودی را بگیرید، پیمانه N را محاسبه کنید تا بتوانید همه اعضا را به گروه‌هایی از 0 تا N-1 انتساب دهید. این گروه می‌تواند از طرف هر تعداد از طرف‌ها مورد توافق قرار گیرد. برای مثال سرورهای مختلف که می‌دانند N=20 است می‌توانند توافق کنند که به ID گروهی که برابر با 57 است، تعلق داشته باشند.
• کاهش خصوصیات: می‌توان با اعداد بر حسب مشخصاتشان رفتار کرد (زوج، مضرب 3 و ...) و مفاهیمی از در این سطح از خصوصیات استنتاج نمود.

==