روش های ارزیابی نتایج خوشه بندی (Clustering Performance) – معیارهای بیرونی (External Index)
«خوشهبندی» (Clustering)، روشی است که در آن دستهبندی یا طبقهبندی نقاط براساس خصوصیات و ویژگیهایشان انجام میشود. این کار اغلب با استفاده از یک «تابع شباهت» (Similarity Function) یا «عدم شباهت» (Dissimilarity) تعریف شده برای سنجش دوری یا نزدیکی نقاط از یکدیگر صورت میپذیرد. البته معمولا تابع عدم شباهت را همان «تابع فاصله» (Distance Function) در نظر میگیرند. هدف از ایجاد خوشهها، تفکیک نقاط به گروههایی است که بیشترین شباهت (کمترین فاصله) را در درون گروهها و کمترین شباهت (بیشترین فاصله) را بین گروهها داشته باشند.


تعلق نقاط به هر خوشه، توسط عمل «برچسبگذاری» (Labeling) انجام میشود. با توجه به انواع مختلف ویژگیها برای نقاط، روشها و الگوریتمهای متنوعی نیز برای خوشهبندی وجود دارد. در نتیجه، ارزیابی نتایج خوشهبندی ملاکی است برای انتخاب الگوریتم مناسب. در این مطلب، شاخصهای ارزیابی بیرونی معرفی و بررسی میشوند.
روشهای ارزیابی نتایج خوشهبندی با معیارهای بیرونی
از آنجایی که «تحلیل خوشهبندی» (Clustering Analysis) یک روش «بدون نظارت» (Unsupervised) محسوب میشود، روشهای ارزیابی و سنجش کارایی آن با روشهای «نظارت شده» (Supervised) تفاوت دارند.
معمولا ارزیابی نتایج خوشهبندی براساس تابع فاصله و برچسبهای تولید شده در تحلیل خوشهبندی انجام میشود. ارزیابی نتایج خوشهبندی میتواند از دو منظر بررسی شود: ارزیابی درونی (Internal Index) و ارزیابی بیرونی (External Index)
منظور از ارزیابی درونی، بررسی دستیابی به اهداف خوشهبندی است. همانطور که گفته شد هدف از خوشهبندی، ایجاد دستههایی با بیشترین شباهت درونی و کمترین شباهت بین دستهها است. در نتیجه در رویکرد ارزیابی درونی خوشهبندی از ترکیب توابع فاصله یا شباهت برای خوشهها استفاده میشود. برای مثال اگر دادهها یک بعدی باشند، «تحلیل واریانس» (Analysis of Variance) میتواند نسبت میانگین تغییرات بین خوشهها را به میانگین تغییرات درون خوشهها اندازهگیری کرده و مشخص کند که آیا خوشهها کاملا از یکدیگر جدا هستند یا خیر.
ولی در روش ارزیابی با معیارهای بیرونی، برای همه نقاط یک «برچسب واقعی» (Benchmark) وجود دارد که نشان دهنده تعلق نقاط به دستهها است. معمولا به برچسبهای واقعی، «استاندارد طلایی» (Gold Standard) نیز میگویند. از طرفی «برچسبهای خوشهبندی» (Clustering Label) نیز کد مربوط به خوشهای است که یک نقطه درون آن قرار دارد. در این متن مجموعه دستهها را با و خوشهها را به صورت نشان میدهیم.
در روش ارزیابی بیرونی، مطابقت این دو گونه برچسب انجام میپذیرد. باید توجه داشت که ممکن است کدهای برچسبهای حاصل از خوشهبندی با برچسبهای واقعی یکسان نباشند. به این معنی که برچسب واقعی ۱ برای یک نقطه بیانگر متعلق بودن آن به دسته شماره ۱ است در حالیکه ممکن است شماره برچسب برای این نقطه در خوشهبندی برابر با ۴ باشد.
مثال ۱
فرض کنید برای ۵ نقطه برچسب واقعی و حاصل از خوشهبندی در جدول زیر قرار داشته باشد. هر چند برچسبها یکسان نیستند ولی هر دو سری برچسب به دسته یا خوشههای یکسانی اشاره دارند.
| مقدار | 5 | 4 | 6 | 2 | 1 |
| برچسب واقعی | 1 | 1 | 1 | 2 | 2 |
| برچسب خوشه | 2 | 2 | 2 | 1 | 1 |
پس هنگام مقایسه برچسبها، باید توجه داشت که عدم مطابقت برچسبهای واقعی با خوشهای ممکن است حاصل از این مسئله باشد. در ادامه به بررسی روشهایی میپردازیم که با در نظر گرفتن این مسئله، مطابقت برچسبهای حاصل از خوشهبندی را با واقعی ارزیابی میکنند.
شاخص خلوص
یکی از سادهترین شاخصهای ارزیابی بیرونی در خوشهبندی، «شاخص خلوص» (Purity Index) است که درصد مطابقت بین برچسبهای خوشهبندی و برچسبهای واقعی را میسنجد. در این حالت برچسب هر خوشه با برچسب واقعی دستهای که بیشترین اشتراک را دارد مطابقت پیدا کرده و تعداد نقاطی از خوشه که در دسته صحیح طبقهبندی شدهاند شمارش میشوند. نسبت این تعداد به تعداد کل نقاط شاخص خلوص را میسازد و شکل محاسباتی آن به صورت زیر است:
باید توجه داشت که منظور از تعداد نقاط مشترک از خوشه با دسته و N نیز تعداد کل نقاط است. با توجه به شیوه محاسبه شاخص خلوص، مشخص است که حداکثر مقدار برای آن ۱ خواهد بود و این در زمانی اتفاق میافتد که برچسبهای حاصل از خوشهبندی کاملا با برچسبهای واقعی مطابقت داشته باشند. همینطور اگر هیچ برچسب خوشهای با برچسب واقعی مطابقت نداشته باشد، این شاخص صفر میشود.
مثال 2
فرض کنید برای ۵ نقطه، برچسبهای واقعی و برچسبهای حاصل از تحلیل خوشهبندی در جدول زیر قرار دارند.
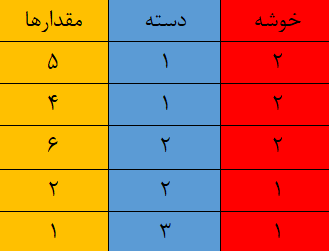
به منظور محاسبه شاخص خلوص، جدول متقاطعی از برچسبها ایجاد میکنیم و محاسبات را طبق فرمول انجام میدهیم. شاخص شفافیت برای خوشههای ایجاد شده برابر است با 0.6 یا 60٪.
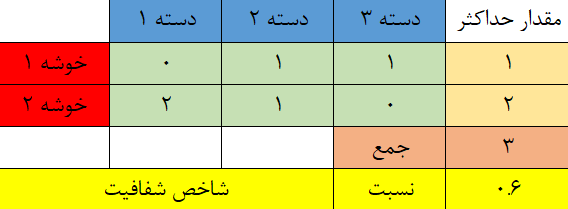
نکته: در این روش احتیاجی نیست که تعداد دستهها با خوشهها برابر باشد. به ماتریس بالا که چنین وضعیتی را نشان میدهد دقت کنید.
خصوصیات شاخص خلوص
سادگی در محاسبات: با توجه به شیوه محاسبه این شاخص، محاسبات طولانی برای بدست آوردن میزان مطابقت لازم نیست.
مستقل از تعداد خوشهها: شاخص خلوص به تعداد خوشهها توجه ندارد. در نتیجه نمیتوان این شاخص را به عنوان معیاری برای سنجش مطابقت تعداد خوشهها نیز در نظر گرفت.
کاهش کارایی با افزایش تعداد خوشهها: اگر تعداد خوشهها زیاد باشد و هیچ هماهنگی نیز بین برچسبهای واقعی و خوشهای وجود نداشته باشد ممکن است شاخص خلوص به ۱ نزدیک شود که یک عیب برای چنین شاخصی است.
شاخص رَند اصلاح شده
برای نشان دادن میزان شباهت بین دو شیوه برچسبگذاری میتوان از «شاخص رَند» (Rand Index) استفاده کرد. این شاخص توسط دانشمند آمار ویلیام رند (William Rand) در سال 1971 در مقالهای با عنوان «معیارهای هدف برای ارزیابی روشهای خوشهبندی» (Objective criteria for the evaluation of clustering methods) معرفی شد.
برای محاسبه آن باید دو پارامتر را اندازهگیری کنیم:
A: تعداد زوجهایی که هم در خوشهها و هم در دستهها در کنار هم هستند. به بیان دیگر هم در خوشهها دارای برچسب یکسانی هستند و هم برچسب دستهها برای آنها یکسان است.
B: تعداد زوجهایی که هم در خوشهها و هم در دستهها از یکدیگر جدا هستند. یعنی برچسب خوشههایشان متفاوت است و البته برچسب دستههای متفاوتی نیز دارند.
مثلا در جدول اطلاعاتی مربوط به مثال ۲، زوجهای در یک دست و در یک خوشه هستند. هرچند ممکن است شماره برچسبهای متفاوتی برای خوشهها یا دستهها وجود داشته باشد. همچنین زوج نیز در دو دسته جدا قرار داشته و ضمناً برچسب خوشههای جداگانه نیز دارند.
حال برای محاسبه شاخص رند کافی است که حاصل جمع A و B را به تعداد کل زوجها تقسیم کنیم.
مثال ۳
اگر برای دادههای مربوط به مثال ۲ شاخص Rand را محاسبه کنیم، مطابقت برچسبهای واقعی و خوشهای را به صورت زیر میتوان مشاهده کرد.

اگر خوشهها مطابق با دستهها ایجاد شده باشند، شاخص رند برابر با ۱ خواهد بود. ولی اگر خوشهبندی به صورت تصادفی ایجاد شده باشد، دلیلی ندارد که مقدار این شاخص برابر با صفر باشد. برای رفع این مشکل از «شاخص رند اصلاح شده» (Adjusted Rand Index) استفاده میشود. این شاخص را به صورت ARI نشان داده و به شکل زیر محاسبه میشود:
منظور از E نیز امید-ریاضی شاخص رند است.
خصوصیات شاخص رند اصلاح شده
حدود مقدارها: ARI مقداری بین ۱ و ۱- خواهد بود. در حالتی که ARI=1 باشد، مطابقت کامل بین برچسبهای واقعی و خوشهای وجود دارد و در مقابل اگر مقدار این شاخص برابر با ۱- باشد نشانگر برچسبگذاری تصادفی در حین خوشهبندی است.
- شاخص کارا برای مقایسه چندین روش: از آنجایی که این شاخص به توافق بین برچسبها تکیه دارد، میتوان از آن برای مقایسه دو روش خوشهبندی نیز استفاده کرد. برای مثال میتوان مطابقت بین شیوه خوشهبندی و برچسبگذاری در الگوریتم k-میانگین را با روش فازی c-means بررسی کرد.
- بدون وابستگی به تعداد خوشهها: با توجه به شیوه محاسبه این شاخص، تفاوت بین تعداد خوشهها و دستهها نیز در آن لحاظ شده است.
- تقارن در ARI: اگر جای دستهها و خوشهها عوض شود، شاخص ARI تعییری نمیکند. به این معنی که .
- عدم حساسیت به تغییر برچسبها: اگر برچسبهای خوشهها تغییر کند در نتیجه ARI تغییری بوجود نمیآید. برای مثال اگر همه برچسبهای ۱ در خوشهبندی به برچسب ۲ تبدیل شوند، حاصل ARI تغییری نخواهد کرد.
اگر جدول متقاطعی از دستهها و خوشهها مانند مثال ۱ ایجاد کنیم، میتوانیم به شیوه دیگری نیز شاخص رند اصلاح شده را محاسبه کنیم.
فرض کنید در اینجا تعداد عناصر مشترک در دسته i و خوشه j باشد. همچنین نیز مجموع مقدارهای برای سطر iام و نیز جمع مقدارهای در ستون jام باشد. جدول متقاطع زیر تعداد عناصر مشترک در بین دستهها و خوشهها را نشان میدهد.

حال براساس محاسبه زیر میتوان شاخص رند اصلاح شده را بدست آورد:
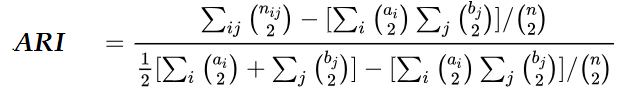
مثال ۴
با توجه به مثال ۲ مقدار شاخص اصلاح شده رند 0.0909 خواهد بود که در مقایسه با مقدار شاخص رند کاملا متفاوت است.
همینطور که دیده میشود، در این حالت عدم مطابقت تعداد خوشهها با دستهها در شاخص بسیار تاثیر گذار است.
شاخص فولکز-مالوز
برای استفاده از این شاخص باید در مورد چند اصطلاح، آگاهی داشته باشید:
- مثبت صحیح: اگر زوجی از مشاهدات که در یک دسته هستند، در یک خوشه نیز قرار بگیرند، نتیجه خوشهبندی را برای این زوج «مثبت صحیح« (True Positive) مینامیم. مثبت صحیح را با TP نیز نشان میدهند.
- منفی صحیح: اگر زوجی از مشاهدات که در دو دسته مجزا قرار دارند، در دو خوشه مجزا نیز جای گیرند، نتیجه خوشهبندی را برای این زوج «منفی صحیح» (True Negative) مینامیم. منفی صحیح را با TN نیز نشان میدهند.
- مثبت کاذب: اگر زوجی از مشاهدات که در دو دسته مجزا قرار دارند، در یک خوشه جای گیرند، نتیجه خوشهبندی برای این زوج «مثبت کاذب» (False Positive) است. مثبت کاذب را با FP نیز نشان میدهند.
- منفی کاذب: اگر زوجی از مشاهدات که در یک دسته قرار دارند به اشتباه در دو خوشه قرار گیرند، نتیجه خوشهبندی برای این زوج «منفی کاذب» (False Negative) است. منفی کاذب را با FN نیز نشان میدهند.
جدول زیر که وظیفه مقایسه بین تعداد نتایج خوشهبندی توسط الگوریتم و دستهبندی اصلی را به عهده دارد، به «ماتریس درهمریختگی» (Confusion Matrix) شهرت دارد که توجه به آن به درک و شیوه محاسبه اشخص فولکر-مالوز و اصطلاحات گفته شده، کمک میکند.
| نتیجه خوشهبندی برای زوج | دستهبندی واقعی | ||
| در یک دسته | در دو دسته مجزا | ||
| خوشهبندی | در یک خوشه | TP | FP |
| در دو خوشه مجزا | FN | TN | |
حال اگر تعداد زوجهای مثبت صحیح را با ، تعداد مثبت کاذب را با و تعداد منفی کاذب را با نشان بدهیم، شاخص «فولکز- مالوز» (Fowlkes-Mallows) که با FMI نشان داده میشود به صورت زیر محاسبه میشود:
مقدار این شاخص نیز بین ۰ تا ۱ تغییر میکند. هر چه FMI به ۱ نزدیکتر باشد، مطابقت بین دو شیوه برچسبگذاری بیشتر است. در صورتی که این شاخص به صفر برسد، خوشهبندی به صورت تصادفی انجام شده.
مثال 5
با توجه به مثال ۱ و ۲ شاخص فولکز-مالوز بر اساس اطلاعات زیر قابل محاسبه است.
| TP=1 | FP=3 |
| FN=1 | TN=5 |
اندازه F
همانطور که دیده شده، استفاده از مفاهیم مثبت کاذب، مثبت صحیح، منفی کاذب و منفی صحیح در محاسبه شاخص ارزیابی نتایج خوشهبندی اهمیت زیادی دارد. با توجه به این مفاهیم میتوان شاخص رند را به صورت زیر نیز محاسبه کرد:
در این حالت وزن یا اهمیت مربوط به منفی کاذب (FN) یا مثبت کاذب (FP) در محاسبه شاخص یکسان است. ولی در «اندازه F» () میتوان وزن آنها را با پارامتر تغییر داد. اگر P و R را به صورت زیر تعریف کنیم:
آنگاه شاخص F را به ازاء به شکل زیر محاسبه میشود:
مثال 6
اندازه برای دادههای مربوط به مثال ۲ برابر است با:
با این کار وزن پارامتر FN بیشتر از FP در نظر گرفته شده است.
اگر به یادگیری مباحث مشابه این مطلب علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
- آموزش خوشه بندی تفکیکی با نرم افزار R
- آموزش خوشه بندی سلسله مراتبی با SPSS
- آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن
- فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی













سپاس از توضیحات مفیدتون.
با عرض سلام و احترام
استاد گرامی
من دو الگوریتم خوشه بندی را برای یک مجموعه داده که شامل 8 ویژگی کمی و کیفی است مورد مقایسه قرار دادم و برای ارزیابی بیرونی می خواهم از معیار ARI استفاده کنم، با توجه به اینکه داده ها شامل True Lable نیستند چگونه می توان از روشهای ارزیابی بیرونی استفاده کرد؟
سپاسگزارم من را در این زمینه راهنمایی کنید.
سلام. ممنونم از مطالبتون
خب میدونیم که خوشه بندی از نوع Unsupervised و معنی اش اینه که ما برای داده ها label نداریم. حالا پس این موضوع برچسب واقعی (Benchmark یا gold standard) دیگه چیه؟ یعنی اگه داده ها label دارند و قراره از این labelها استفاده بشه (حتی برای ارزیابی الگوریتم) میشه supervised و نیازی به clustering نداریم
یا اگه من بد فهمیدم خواهش میکنم راهنمایی بفرمایید
سلام و درود
از اینکه همراه مجله فرادرس هستید بسیار سپاسگزاریم.
آنچه به عنوان ایراد به مشخص کردن برچسب فرمودید، کاملا صحیح است. ولی توجه داشته باشید که در نظر گرفتن برچسبهای واقعی فقط زمانی مورد نظر است که بخواهیم یک روش خوشهبندی را با روش دیگر مقایسه کنیم و کارایی هر یک را بسنجیم. در نتیجه براساس مشاهدات برچسب دار، سعی در پیدا کردن بهترین الگوریتم میکنیم. در اینجا خوشهبندی هدف نیست بلکه ارزیابی روش خوشهبندی موضوع بحث است.
به این ترتیب مجموعه دادهای که از قبل برچسبگذاری شده را مبنا قرار داده و مشخص میکنیم که نتیجه روش خوشهبندی (بدون در نظر گرفتن برچسبها) چقدر با برچسبهای واقعی همخوانی دارد.
به همین دلیل شاخصهای ارائه شده از نوع بیرونی هستند یعنی با الگویی خارج از خوشهها، الگوریتم سنجیده میشود.
اما استفاده از معیارهای درونی، بدون در نظر گرفتن برچسب عمل میکند و فقط ویژگیها اصلی بهینه برای خوشهها را در نظر میگیرد.
شاد و تندرست باشید.
خیلی عالی بود سپاس
خیلی خوب توضیح داده بودین
سپاسگزارم
اگر براتون مقدره ممکنه معیار ارزیابی Bcubed رو هم با مثال شرح بدین و فرق آن را با f-measure بفرمایید