توزیع لوگ نرمال (Log-normal Distribution) — به زبان ساده

در تئوری آمار و احتمال، توزیع «لوگ نرمال» (Log-normal) به عنوان یک توزیع پیوسته، برای بیان رفتار بعضی از پدیده‌های احتمالی، به کار می‌رود. اگر متغیر تصادفی $$X$$ دارای توزیع لوگ نرمال باشد، آنگاه توزیع $$Y=\ln(X)$$ نرمال است. به همین ترتیب می‌توان گفت، اگر $$Y$$ توزیع نرمال داشته باشد، آنگاه $$X=\operatorname{EXP}(Y)$$ دارای توزیع «لاگ نرمال» است.

به دلیل ارتباط بین توزیع نرمال و توزیع لوگ نرمال، بهتر است ابتدا مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را بخوانید. همچنین برای اطلاع از انواع توزیع‌های آماری خواندن مطلب توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس نیز خالی از لطف نیست.

توزیع لوگ نرمال (Log-normal Distribution)

توزیع «لاگ نرمال» از نوع توزیع‌های پیوسته و دارای تکیه‌گاه مثبت است. در نتیجه اگر متغیر تصادفی $$X$$ دارای توزیع لاگ نرمال باشد، مطمئن هستیم که $$X>0$$ است. این توزیع را گاهی به نام «توزیع گالتون» (Galton Distribution) نیز می‌شناسند، زیرا «فرانسیس گالتون» (Francis Galton) دانشمند و آمارشناس انگلیسی در تحقیقاتش در قرن 1۹ به این توزیع پرداخته است.

فیلم آموزش مقدماتی نظریه قابلیت اعتماد در فرادرس

کلیک کنید

از این توزیع برای بیان پدیده‌های تصادفی که به صورت تجمعی و افزایشی تغییر می‌یابند، استفاده می‌شود. برای مثال می‌توان توزیع احتمالی برای پدیده‌های تصادفی زیر را از نوع لوگ نرمال در نظر گرفت:

• طول یادداشت‌های مربوط به یک موضوع در انجمن‌های اینترنتی
• زمان انجام بازی شطرنج
• مدت زمان مقایسه و تشخیص یک محرک صوتی با یک محرک استاندارد
• تغییرات مساحت پوسته یک موجود زنده
• شمارش دنباله‌ RNA استاندارد شده برای هر ناحیه ژنی
• ...

تابع چگالی و تابع توزیع تجمعی متغیر تصادفی لوگ نرمال

به عنوان تعریف متغیر تصادفی با توزیع لوگ نرمال می‌توان گفت که اگر یک متغیر تصادفی مانند $$X$$‌ دارای توزیع لوگ نرمال با پارامترهای $$\mu$$ و $$\sigma^2$$ باشد، آنگاه توزیع $$\ln(X)\sim N(\mu,\sigma^2)$$، نرمال خواهد بود.

با توجه به رابطه‌ای که بین توزیع نرمال و توزیع لوگ نرمال وجود دارد، می‌توان به روش زیر تابع چگالی متغیر تصادفی $$X$$ را به صورت زیر محاسبه کرد. البته توجه داشته باشید که در رابطه‌های زیر منظور از $$\Phi$$‌ تابع توزیع تجمعی نرمال استاندارد است. همچنین $$\phi$$ نیز تابع چگالی احتمال نرمال استاندارد را نشان می‌دهد. از طرفی می‌دانیم که تابع چگالی از طریق مشتق‌گیری از تابع توزیع تجمعی حاصل می‌شود. به این ترتیب براساس این توضیحات مراحل محاسبه تابع چگالی توزیع لوگ نرمال را پی‌میگیریم.

$$\large \begin{aligned}f_{X}(x)&={\frac {\rm {d}}{{\rm {d}}x}}\Pr(X\leq x)={\frac {\rm {d}}{{\rm {d}}x}}\Pr(\ln X\leq \ln x)\\ \large &={\frac {\rm {d}}{{\rm {d}}x}}\Phi \left({\frac {\ln x-\mu }{\sigma }}\right)\\ \large &=\phi \left({\frac {\ln x-\mu }{\sigma }}\right){\frac {\rm {d}}{{\rm {d}}x}}\left({\frac {\ln x-\mu }{\sigma }}\right)\\\large &=\phi \left({\frac {\ln x-\mu }{\sigma }}\right){\frac {1}{\sigma x}}\\ \large &={\frac {1}{x}}\cdot {\frac {1}{\sigma {\sqrt {2\pi \,}}}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right)\end{aligned}$$

همانطور که دیده می‌شود، تابع چگالی حاصل، بسیار شبیه به توزیع نرمال است. نمودار مربوط به توزیع لوگ نرمال در تصویر زیر دیده می‌شود.

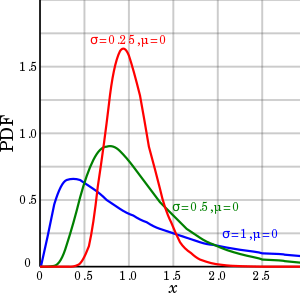
همانطور که در تصویر دیده می‌شود، تکیه‌گاه (مجموعه مقادیر متغیر تصادفی) در این توزیع مثبت است. همچنین وجود چولگی زیاد این توزیع بخصوص برای مقدارهای بزرگ $$\sigma$$ کاملا واضح است.

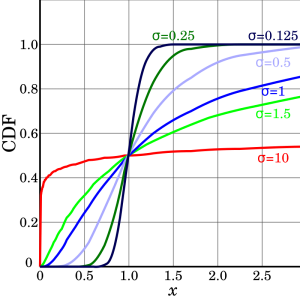
از طرفی تابع توزیع احتمال تجمعی برای متغیر تصادفی لوگ نرمال به شکل زیر نمایش داده می‌شود.

$$\large F_{X}(x)=\Phi ({\frac {(\ln x)-\mu }{\sigma }})$$

نمودار تابع توزیع تجمعی این متغیر تصادفی نیز در شکل زیر دیده می‌شود.

خصوصیات متغیر تصادفی لوگ نرمال

همانطور که در تعریف پارامترهای توزیع لوگ نرمال مشخص شد، شیوه بیان برای توزیع متغیر تصادفی $$X$$ به صورت $$X\sim Lognormal(\mu ,\sigma^2)$$ است. ولی باید دقت کرد که این پارامترها به عنوان میانگین و واریانس توزیع لوگ نرمال محسوب نمی‌شوند. برای محاسبه امید ریاضی و واریانس متغیر تصادفی با توزیع لوگ نرمال باید از میانگین و واریانس توزیع نرمال استفاده کرد. به این ترتیب برای محاسبه امید ریاضی متغیر تصادفی لوگ نرمال خواهیم داشت:

$$\large E(X)=\operatorname{EXP}(\mu+\frac{\sigma^2}{2})$$

در تصویر زیر رابطه بین تابع چگالی احتمال و امید ریاضی متغیر تصادفی لوگ نرمال و نرمال را مشاهده می‌کنید. مشخص است که این رابطه به واسطه یک تابع نمایی ($$x=e^y$$) ایجاد شده است.

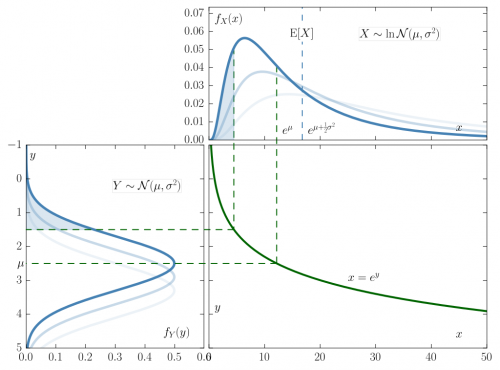
همچنین واریانس چنین متغیر تصادفی به شکل زیر قابل محاسبه خواهد بود.

$$\large \operatorname{Var}(X)= [\exp(\sigma ^{2})-1]\operatorname{EXP}(2\mu +\sigma ^{2})$$

البته برای محاسبه میانه و نما به صورت زیر عمل می‌کنیم.

$$\large \operatorname{Median}(X)=\operatorname{EXP}(\mu)$$

$$\large \operatorname{Mode}(X)=\operatorname{EXP}(\mu-\sigma^2)$$

در تصویر زیر نیز نمودار مربوط به توزیع لوگ نرمال به همران میانگین، میانه و نمای این توزیع قابل مشاهده است.

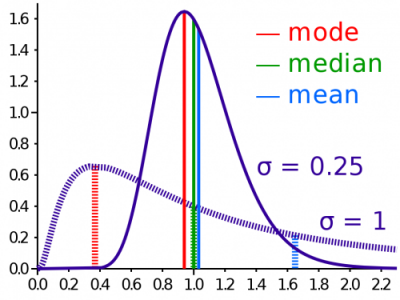
ارتباط با توزیع‌های دیگر

در این قسمت به بررسی ارتباطی که توزیع لوگ نرمال با توزیع‌های دیگر دارد می‌پردازیم. البته مشخص است که به علت وابستگی زیاد بین توزیع نرمال و لوگ نرمال، بسیاری از خصوصیات و ارتباط آن‌ها با دیگر توزیع‌ها، مشابه باشد.

فیلم آموزش کاربرد آمار در برنامه ریزی نگهداری و تعمیرات (رایگان) در فرادرس

کلیک کنید

براساس تعریفی که برای متغیر تصادفی لوگ نرمال ارائه شد، ارتباط این توزیع با توزیع‌های دیگر در فهرست زیر مشاهده می‌شود.

• اگر $$X\sim N(\mu.\sigma^2)$$ باشد آنگاه $$\exp(X)\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$$ یعنی تابع نمایی با پایه طبیعی متغیر تصادفی $$X$$ دارای توزیع نرمال با همان پارامترهای توزیع لوگ نرمال است.
• اگر $$ X\sim \operatorname {Lognormal} (\mu ,\sigma ^{2})$$ آنگاه توزیع لگاریتم طبیعی $$X$$ به صورت نرمال با همان پارامترهای توزیع لوگ نرمال است، یعنی $$ \ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})$$
• اگر $$X_i$$ها n متغیر تصادفی مستقل با توزیع لوگ نرمال با پارامترهای $$\mu_i$$ و $$\sigma^2_i$$ باشند، آنگاه توزیع حاصلضرب آن‌ها یعنی $$Y=\textstyle \prod _{i=1}^{n}X_{i}$$ به صورت لوگ نرمال با پارامترهای $$\sum _{i=1}^{n}\mu _{i}$$ و $$ \sum _{i=1}^{n}\sigma _{i}^{2}$$ است. به این ترتیب خواهیم داشت: $$Y\sim \operatorname {Lognormal} {\Big (}\textstyle \sum _{i=1}^{n}\mu _{i},\ \sum _{i=1}^{n}\sigma _{i}^{2}{\Big )}$$.
• براساس پاراگراف قبلی می‌توان نشان داد که متغیر تصادفی حاصل از $$a$$ بار ضرب متغیر تصادفی $$X$$ در خودش، متغیر تصادفی لوگ نرمال با پارامترهای $$a\mu$$ و $$a^2\sigma^2$$ ایجاد خواهد کرد.
• برای متغیر تصادفی $$X$$ با توزیع لوگ نرمال، داریم $$aX\sim \operatorname {Lognormal} (\mu +\ln a,\ \sigma ^{2})$$. به این معنی که ضرب کردن متغیر تصادفی لوگ نرمال در مقدار ثابت $$a$$، باعث افزایش مقدار $$ln(A)$$ به پارامتر اول توزیع لاگ نرمال می‌شود.

به منظور شبیه‌سازی داده‌های با توزیع لوگ نرمال، بهتر است به تعداد مورد نیاز عدد تصادفی از توزیع نرمال با پارامترهای $$\mu$$ و $$\sigma^2$$ تولید کرده ($$X$$) و با توجه به رابطه زیر آن‌ها را به توزیع لوگ نرمال ($$Y$$) تبدیل کرد.

$$\large Y=\exp(X)$$

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آمار و احتمال مهندسی
• توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس

^^