مسئله فروشنده دوره گرد در جاوا — به زبان ساده

در این راهنما در مورد الگوریتم «تبرید شبیه‌سازی‌ شده» (Simulated Annealing) صحبت خواهیم کرد و مثالی از پیاده‌سازی آن را بر مبنای مسئله فروشنده دوره گرد (TSP) ارائه می‌کنیم.

تبرید شبیه‌سازی‌ شده

الگوریتم شبیه‌سازی‌شده یک راه‌حل شهودی برای حل کردن مسائلی با فضای جستجوی بزرگ محسوب می‌شود. نام و منبع الهام این الگوریتم از موضوع تبرید در متالوژی ناشی می‌شود. این تکنیکی است که در آن حرارت‌دهی و خنک کردن کنترل‌شده یک ماده صورت می‌گیرد.

فیلم آموزش شبیه سازی تبرید Simulated Annealing در متلب MATLAB در فرادرس

کلیک کنید

به طور کلی تبرید شبیه‌سازی‌ شده موجب کاهش احتمال پذیرش راه‌حل‌های نادرست در زمان کاوش فضای راه‌حل و کاهش دمای سیستم می‌شود. انیمیشن زیر سازوکار یافتن بهترین راه‌حل را با الگوریتم تبرید شبیه‌سازی‌ شده نمایش می‌دهد:

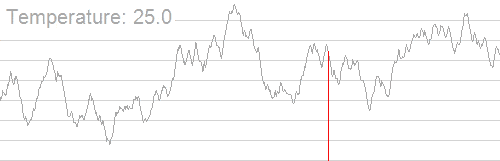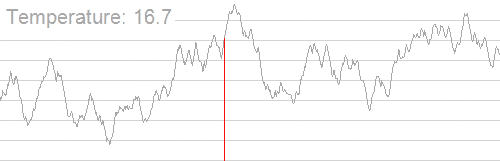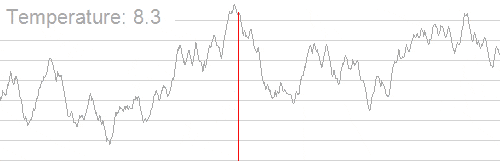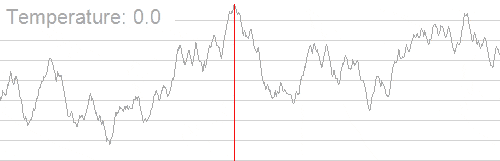
همان طور که مشاهده می‌کنید؛ الگوریتم از یک بازه وسیعی از راه‌حل با دمای بالای سیستم استفاده می‌کند و به دنبال نقطه بهینه سراسری می‌گردد. زمانی که دما کاهش می‌یابد، بازه جستجو کوچک‌تر می‌شود تا این که به بهینه سراسری می‌رسد.

این الگوریتم چند پارامتر دارد که با آن‌ها کار می‌کند:

• تعداد تکرارها: شرط توقف برای شبیه‌سازی است.
• دمای اولیه: انرژی آغازین سیستم است.
• پارامتر نرخ خنک‌سازی: درصد کاهش دمای سیستم را تعیین می‌کند.
• کمینه دما: شرایط اختیاری توقف است.
• زمان شبیه‌سازی: شرایط اختیاری توقف است.

مقادیر این پارامترها باید به دقت انتخاب شوند، چون ممکن است تأثیر زیادی روی عملکرد فرایند بگذارند.

مسئله فروشنده دوره‌گرد

مسئله فروشنده دوره‌گرد (TSP) شناخته‌شده‌ترین مسئله بهینه‌سازی رایانه در دنیای مدرن محسوب می‌شود. به بیان ساده این مسئله به یافتن مسیر بهینه بین گره‌های یک گراف گفته می‌شود. مسافت کلی سفر می‌تواند یکی از معیارهای سفر باشد.

فیلم آموزش حل مساله فروشنده دوره گرد با الگوریتم ژنتیک در فرادرس

کلیک کنید

مدل جاوا

برای حل مسئله TSP باید کلاس‌های مدل را که City و Travel نام دارند در اختیار داشته باشیم. در کلاس اول شرایط گره‌ها را در گراف ذخیره می‌کنیم:

1@Data
2public class City {
3 
4    private int x;
5    private int y;
6 
7    public City() {
8        this.x = (int) (Math.random() * 500);
9        this.y = (int) (Math.random() * 500);
10    }
11 
12    public double distanceToCity(City city) {
13        int x = Math.abs(getX() - city.getX());
14        int y = Math.abs(getY() - city.getY());
15        return Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
16    }
17 
18}

متد سازنده کلاس City، امکان ایجاد موقعیت‌های تصادفی شهرها را به ما می‌دهد. منطق (..)distanceToCity مسئول محاسبه مسافت بین شهرها است.

کد زیر مسئول مدل‌سازی گردش یک فروشنده دوره‌گرد است. کار خود را با ایجاد ترتیب اولیه شهرها در سفر آغاز می‌کنیم:

1public void generateInitialTravel() {
2    if (travel.isEmpty())
3        new Travel(10);
4    Collections.shuffle(travel);
5}

علاوه بر ایجاد مسیر اولیه، باید متدهایی برای تعویض دو شهر تصادفی در ترتیب سفر نیز تهیه کنیم. ما از آن برای جستجوی راه‌حل‌های بهتر درون الگوریتم تبرید شبیه‌سازی‌ شده استفاده می‌کنیم:

1public void swapCities() {
2    int a = generateRandomIndex();
3    int b = generateRandomIndex();
4    previousTravel = travel;
5    City x = travel.get(a);
6    City y = travel.get(b);
7    travel.set(a, y);
8    travel.set(b, x);
9}

افزون بر آن باید یک متد برای بازگرداندن تعویض ایجاد شده در مرحله قبلی نیز داشته باشیم که اگر راه‌حل جدید پذیرفته نشود مورد استفاده قرار می‌گیرد:

1public void revertSwap() {
2    travel = previousTravel;
3}

آخرین متد که باید داشته باشیم، محاسبه مسافت کلی سفر است که به عنوان معیار بهینه بودن استفاده می‌شود:

1public int getDistance() {
2    int distance = 0;
3    for (int index = 0; index < travel.size(); index++) {
4        City starting = getCity(index);
5        City destination;
6        if (index + 1 < travel.size()) {
7            destination = getCity(index + 1);
8        } else {
9            destination = getCity(0);
10        }
11            distance += starting.distanceToCity(destination);
12    }
13    return distance;
14}

اینک روی بخش اصلی مسئله یعنی پیاده‌سازی الگوریتم تبرید شبیه‌سازی‌ شده متمرکز می‌شویم.

پیاده‌سازی الگوریتم تبرید شبیه‌سازی‌ شده

در پیاده‌سازی زیر برای الگوریتم تبرید شبیه‌سازی‌ شده قصد داریم مسئله TSP را حل کنیم. به عنوان یادآوری باید بگوییم که هدف ما یافتن کوتاه‌ترین مسافت برای سفر بین دو شهر است.

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

برای آغاز فرایند باید سه پارامتر اصلی یعنی startingTemperature ،numberOfIterations و coolingRate را ارائه کنیم:

1public double simulateAnnealing(double startingTemperature,
2  int numberOfIterations, double coolingRate) {
3    double t = startingTemperature;
4    travel.generateInitialTravel();
5    double bestDistance = travel.getDistance();
6 
7    Travel currentSolution = travel;
8    // ...
9}

پیش از آغاز شبیه‌سازی، ترتیب اولیه (تصادفی) شهرها را ایجاد و مسافت کلی سفر را محاسبه می‌کنیم. از آنجا که این نخستین محاسبه مسافت است باید آن را درون متغیر bestDistance همراه با currentSolution ذخیره کنیم.

در گام بعدی یک حلقه شبیه‌سازی‌های اصلی را آغاز می‌کنیم:

1for (int i = 0; i < numberOfIterations; i++) {
2    if (t > 0.1) {
3        //...
4    } else {
5        continue;
6    }
7}

این حلقه به تعداد تکرارهایی که تعیین‌شده اجرا می‌شود. به علاوه یک شرط نیز برای توقف آن تعیین کرده‌ایم که به صورت کاهش دما به کمتر از 0.1 است. بدین ترتیب می‌توانیم در زمان شبیه‌سازی‌ها صرفه‌جویی کنیم، زیرا در دماهای پایین، اختلاف بهینه‌سازی‌ها چندان درخور توجه نیست. در ادامه منطق اصلی الگوریتم تبرید شبیه‌سازی‌ شده را می‌بینید:

1currentSolution.swapCities();
2double currentDistance = currentSolution.getDistance();
3if (currentDistance < bestDistance) {
4    bestDistance = currentDistance;
5} else if (Math.exp((bestDistance - currentDistance) / t) < Math.random()) {
6    currentSolution.revertSwap();
7}

یافتن کوتاه‌ترین مسافت

در هر گام از شبیه‌سازی به صورت تصادفی دو شهر را در ترتیب سفر قرار می‌دهیم. به علاوه currentDistance را محاسبه می‌کنیم، اگر مسافت جدید پایین‌تر از bestDistance باشد، آن را به عنوان بهترین نتیجه (bestDistance) ذخیره می‌کنیم.

در غیر این صورت بررسی می‌کنیم که آیا تابع بولتزمان احتمال توزیع پایین‌تر از مقدار انتخاب شده تصادفی در بازه 0 تا 1 است یا نه. اگر چنین بود شهرها را عوض می‌کنیم؛ در غیر این صورت ترتیب جدید شهرها را نگه می‌داریم، چون به ما کمک می‌کند که از کمینه‌های موضعی احتراز کنیم. در نهایت در هر گام از شبیه‌سازی دما را به میزان coolingRate کاهش می‌دهیم:

1t *= coolingRate;

پس از این که شبیه‌سازی پایان یافت، بهترین راه‌حل را که با استفاده از الگوریتم تبرید شبیه‌سازی‌ شده به دست آمده است، بازگشت می‌دهیم. در ادامه چند نکته در مورد انتخاب پارامترهای بهترین شبیه‌سازی ارائه شده که باید مورد توجه قرار دهید:

• در فضاهای راه‌حل کوچک بهتر است دمای آغازین پایین باشد و نرخ خنک‌سازی کاهش یابد تا زمان شبیه‌سازی بدون تأثیر منفی روی کیفیت، پایین بماند.
• برای فضاهای راه‌حل بزرگ‌تر بهتر است نرخ آغازین دما بالا باشد و نرخ خنک‌سازی کم انتخاب شود، چون ممکن است کمینه‌های موضعی زیادی وجود داشته باشند.
• همواره زمان کافی برای شبیه‌سازی از دماهای بالا تا پایین در اختیار سیستم قرار دهید.

فراموش نکنید که پیش از آغاز شبیه‌سازی‌های اصلی، زمان بیشتری را صرف تنظیم الگوریتم با وهله‌های کوچک‌تر مسئله بکنید، چون موجب بهبود نتیجه نهایی می‌شود.

سخن پایانی

در این راهنمای کوتاه با الگوریتم تبرید شبیه‌سازی‌ شده آشنا شدیم و مسئله فروشنده دوره‌گرد را حل کردیم. امیدواریم این مطلب میزان کارآمد بودن این الگوریتم ساده را در زمان استفاده برای انواع خاصی از مسائل بهینه‌سازی به شما نشان داده باشد. برای مشاهده کد کامل این پیاده‌سازی به این آدرس گیت‌هاب (+) مراجعه کنید.

فیلم مجموعه آموزش جاوا Java – مقدماتی تا پیشرفته در فرادرس

کلیک کنید