آنتروپی اطلاعات – مبانی اولیه
در تئوری اطلاعات، آنتروپی اطلاعات یا به صورت دقیقتر، آنتروپی شانون، امید ریاضی (میانگین) اطلاعات موجود در هر پیام دریافت شده است. در اینجا «پیام» لزوما متن نیست و هر جریانی از اطلاعات میتواند باشد. آنتروپی هر پیام، مقدار عدم قطعیت آن است. هرچه پیام تصادفیتر باشد مقدار آن افزایش ، و هرچه کمتر تصادفی باشد مقدار آن کاهش مییابد. مقصود در اینجا این است که هرچه یک رویداد، کمتر تصادفی باشد، در زمان رخداد اطلاعات بیشتری را فراهم میکند.
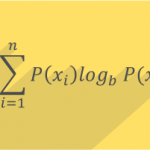
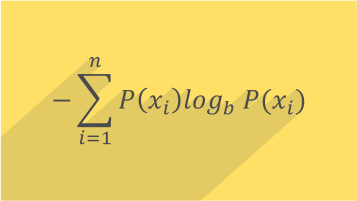
در ابتدا این قضیه وارونه به نظر میرسد: اینطور تصور میشود که پیامهایی که ساختاریافتهتر هستند، حاوی اطلاعات بیشتری باشند، اما چنین نیست. برای مثال، پیام «آآآآآآ» که به نظر بسیار ساختار یافته و غیرتصادفی به نظر میرسد، که گرچه میتواند از یک فرایند تصادفی ایجاد شده باشد، حاوی اطلاعات کمتری نسبت به پیام «الفبا» است. پیام الفبا را میتوان تا حدودی ساختار یافته اما تصادفیتر دانست. همچنین، پیام «آبستیخدم2» را باید یک پیام کاملا تصادفی ذکر کرد.
مفهوم اطلاعات
در تئوری اطلاعات، «اطلاعات» لزوما به معنای اطلاعات مفید نیستند، بلکه تنها مقدار تصادفی بودن پیام را مشخص میکند. بنابراین در مثال بالا، پیام اول دارای کمترین اطلاعات و پیام آخر دارای بیشترین اطلاعات است، هرچند که در اصطلاح روزمره، پیام میانی، یعنی «الفبا» شامل اطلاعات بیشتری نسبت به رشتههایی از حروف تصادفی خواهد بود. بنابراین، در تئوری اطلاعات، پیام اول دارای آنتروپی کمی است، پیام دوم آنتروپی بالاتری از اولی، و پیام سوم بیشترین آنتروپی را دارد
بیت و شانون
به صورت فنیتر، دلایلی برای تعریف اطلاعات به صورت منفی لگاریتم توزیع احتمال وجود دارد که در زیر به بیان آنها خواهیم پرداخت. توزیع احتمال رویدادها، در کنار مقدار اطلاعات هر رویداد، یک متغیر تصادفی را تشکیل میدهد که میانگین آن (امید ریاضی آن) برابر با میانگین مقدار اطلاعات یا به عبارت دیگر آنتروپی آن است که توسط این توزیع تولید میشود. واحد آنتروپی، وابسته به پایه لگاریتم استفاده شده برای تعریف آن، «شانون» (Shannon)، «نات» (Nat) یا «هارتلی» (Hartley) است و به واحد شانون، به طور معمول یک بیت گفته میشود.

از آنجا که لگاریتم توزیع احتمال برای منابع مستقل به صورت افزایشی میباشد، به عنوان معیاری برای اندازهگیری آنتروپی بسیار مفید است. برای مثال، آنتروپی یک بار پرتاب سکه برابر 1 شانون، و برای m بار پرتاب سکه برابر m شانون است. به صورت کلی، شما برای نمایش متغیری که میتواند یکی از n مقدار را بگیرد به (log2(n بیت نیاز دارید، اگر n توانی از 2 باشد. در صورتیکه این مقادیر، احتمال برابری داشته باشند، آنتروپی (در واحد شانون) برابر با تعداد بیتهاست.
شرط برابری بیت و شانون
برابری بین تعداد بیت و شانون تنها وقتی اتفاق میافتد که احتمال وقوع تمام خروجیها برابر باشد. اگر احتمال وقوع یکی از رویدادها بیشتر از بقیه باشد، مشاهده آن رویداد حاوی اطلاعات کمتری است. به صورت برعکس، مشاهده رویدادهای نادرتر، در هنگام رخداد، اطلاعات بیشتری فراهم میکنند. از آنجا که مشاهده رویدادهای نادرتر کمتر اتفاق میافتد، اثر این است که آنتروپی (به عنوان میانگین اطلاعات) دریافتی از داده با توزیع غیریکنواخت کمتر از از (log2(n است. آنتروپی صفر است اگر وقوع یک خروجی، قطعی باشد.
آنتروپی شانون تمام این مقادیر را وقتی توزیع احتمال منبع شناخته شده باشد، مشخص میکند. مفهوم رویدادهای مشاهده شده (یعنی معنی پیامها) در تعریف آنتروپی نقشی ندارد. آنتروپی تنها احتمال مشاهده یک رویداد خاص را در نظر میگیرد، بدین ترتیب اطلاعاتی که حاوی آنهاست اطلاعاتی در مورد توزیع احتمال است، و نه مفهوم خود رویدادها. به صورت کلی، آنتروپی به عدم قطعیت یا بینظمی اشاره میکند. آنتروپی شانون در سال 1948 در مقالهای تحت عنوان «یک نظریه ریاضی برای ارتباطات» توسط کلاود شانون مطرح شد.

اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:












خیلی عالی بود
من برای درس داده کاوی استفاده کردم.
سلام خسته نباشید این مبحث مرتبط با کدامیک از آموزشهای فرادرس هست؟