پیاده سازی درخت دودویی در کاتلین (Kotlin) — از صفر تا صد

در این راهنما عملیات مقدماتی را برای یک درخت دودویی با استفاده از زبان برنامه‌نویسی کاتلین معرفی می‌کنیم. بدین ترتیب با پیاده‌سازی درخت دودویی در کاتلین آشنا می‌شویم.

تعریف

در حوزه برنامه‌نویسی، درخت دودویی به درختی گفته می‌شود که در آن هر گره بیش از دو گره فرزند نداشته باشد. هر گره شامل مقادیری داده است که کلید نامیده می‌شود. ما می‌توانیم بدون از دست دادن تعمیم‌پذیری، ملاحظه خود را محدود به مواردی کنیم که کلیدها صرفاً اعداد صحیح باشند. بنابراین می‌توانیم یک نوع داده بازگشتی به صورت زیر تعریف کنیم:

1class Node(
2    var key: Int,
3    var left: Node? = null,
4    var right: Node? = null)

این نوع داده شامل یک مقدار (کلید فیلد با مقدار صحیح) و یک ارجاع اختیاری به گره‌های فرزند چپ و راست است که از همان نوع والد خود هستند. چنان که مشاهده می‌کنیم به دلیل ماهیت لینک شده، کل درخت دودویی را می‌توان با صرفاً یک گره که گره ریشه نامیده می‌شود توصیف کرد.

در صورتی که مقداری محدودیت روی ساختار درخت اعمال کنیم، همه چیز جالب‌تر خواهد شد. در این راهنما فرض می‌کنیم که درخت، یک درخت دودویی مرتب است (که به نام درخت جستجوی دودویی نیز شناخته می‌شود). این بدان معنی است که گره‌ها با نوعی ترتیب چیدمان یافته‌اند. ما فرض می‌کنیم که همه شرایط زیر در مورد درخت ما صدق می‌کنند:

1. درخت شامل هیچ کلید تکراری نیست.
2. در هر گره، کلید بزرگ‌تر از کلید گره‌های زیردرخت چپ آن است.
3. در هر گره، کلید کمتر از کلید گره‌های زیردرخت راست آن است.

عملیات مقدماتی

برخی از رایج‌ترین عملیات این نوع درخت شامل موارد زیر هستند:

• جستجو برای یک گره با مقدار مفروض
• درج یک مقدار جدید
• حذف یک مقدار موجود
• بازیابی گره‌ها با ترتیب معین

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

گشتن

زمانی که درخت مرتب باشد، فرایند گشتن (Lookup) بسیار کارآمد می‌شود. اگر مقدار مورد جستجو برابر با مقدار گره جاری باشد، در این صوت گشتن به پایان می‌رسد. اگر مقدار مورد جستجو بزرگ‌تر از گره جاری باشد، در این صورت باید زیردرخت چپ کنار گذاشته شود و صرفاً زیردرخت راست جستجو شود:

1fun find(value: Int): Node? = when {
2    this.value > value -> left?.findByValue(value)
3    this.value < value -> right?.findByValue(value)
4    else -> this
5}

توجه کنید که مقدار مورد نظر ممکن است در میان کلیدهای درخت حضور نداشته باشد و از این رو نتیجه‌ی جستجو ممکن است مقدار null بازگشت دهد. همچنین توجه داشته باشید که ما از کلیدواژه when در Kotlin استفاده کرده‌ایم که معادل جاوای آن به همراه گزاره switch-case است، اما قدرت و انعطاف‌پذیری بسیار بیشتری دارد.

درج

از آنجا که درخت امکان حضور هیچ نوع کلید تکراری را نمی‌دهد، درج یک مقدار جدید کاملاً آسان است:

1. اگر مقدار قبلاً موجود باشد، هیچ اقدامی صورت نمی‌گیرد.
2. اگر مقدار موجود نباشد، در گرهی درج می‌شود که جایگاه راست یا چپ آن خالی است.

بنابراین می‌توانیم به صورت بازگشتی درخت را به دنبال زیردرخت‌هایی که می‌توانند این مقدار را در خود بپذیرند مورد جستجو قرار دهیم. زمانی که مقدار کمتر از کلید گره جاری باشد، زیردرخت چپ آن را در صورت وجود برمی‌داریم. اگر موجود نباشد، بدان معنی است که مکان درج مقدار مورد نظر را یافته‌ایم. این همان فرزند چپ گره جاری است.

در حالتی که مقدار بزرگ‌تر از کلید گره جاری باشد، به طور مشابه عمل می‌کنیم. تنها حالت ممکن این است که مقدار برابر با کلید گره جاری باشد. این بدان معنی است که مقدار مورد نظر از قبل در درخت وجود دارد و کار دیگری لازم نیست انجام دهیم:

1fun insert(value: Int) {
2    if (value > this.key) {
3        if (this.right == null) {
4            this.right = Node(value)
5        } else {
6            this.right.insert(value)
7        }
8    } else if (value < this.key) {
9        if (this.left == null) {
10            this.left = Node(value)
11        } else {
12            this.left.insert(value)
13        }
14    }

حذف

ابتدا باید گرهی را که شامل مقدار مفروض است شناسایی کنیم. همانند فرایند گشتن، می‌توانیم درخت را در جستجوی گره اسکن کنیم و ارجاعی به والد گره مورد نظر نگه داریم:

1fun delete(value: Int) {
2    when {
3        value > key -> scan(value, this.right, this)
4        value < key -> scan(value, this.left, this)
5        else -> removeNode(this, null)
6    }
7}

سه حالت متمایز وجود دارند که ممکن است در زمان تلاش برای حذف گره از درخت دودویی با آن‌ها مواجه شویم. ما این حالت‌ها را بر مبنای تعداد گره‌های فرزند غیر تهی دسته‌بندی کرده‌ایم.

هر دو گره فرزند تهی باشند

مدیریت این حالت کاملاً آسان است و تنها حالتی است که ممکن است نتوانیم گره را حذف کنیم، چون اگر گره همان گره ریشه باشد امکان حذف آن وجود نخواهد داشت. در غیر این صورت کافی است گره متناظر والد را برابر با null قرار دهیم.

پیاده‌سازی این رویکرد به صورت زیر است:

1private fun removeNoChildNode(node: Node, parent: Node?) {
2    if (parent == null) {
3        throw IllegalStateException("Can not remove the root node without child nodes")
4    }
5    if (node == parent.left) {
6        parent.left = null
7    } else if (node == parent.right) {
8        parent.right = null
9    }
10}

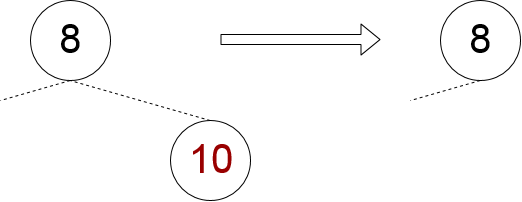
یک فرزند تهی و دیگری غیر تهی باشد

در این حالت، باید همواره تنها گره فرزند را به گرهی که قرار است حذف شود انتقال دهیم.

پیاده‌سازی آن به صورت زیر است:

1private fun removeSingleChildNode(parent: Node, child: Node) {
2    parent.key = child.key
3    parent.left = child.left
4    parent.right = child.right
5}

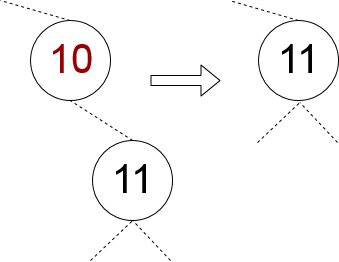
هر دو گره غیر تهی هستند

این حالت پیچیده‌تر است، زیرا باید گرهی را پیدا کنیم که جایگزین گرهی می‌شود که می‌خواهیم حذف کنیم. یک روش برای یافتن این گره جایگزین آن است که یک گره را از زیردرخت چپ با بزرگ‌ترین کلید برداریم. روش دیگر دقیقاً متقارن روش فوق است. ما باید گرهی را در زیردرخت راست با کوچک‌ترین کلید برداریم. ما در این نوشته از رویکرد اول استفاده می‌کنیم:

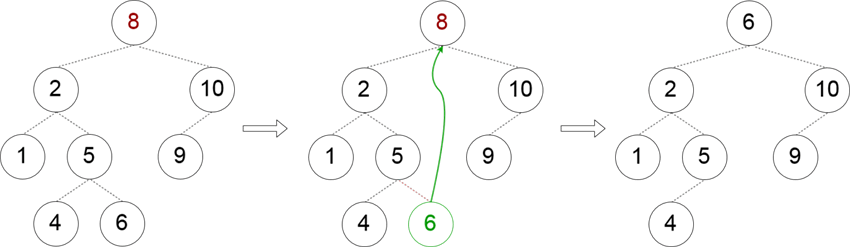
زمانی که گره جایگزین پیدا شد، می‌توانیم ارجاع به آن را از گره والدش حذف کنیم. این بدان معنی است که وقتی برای گره جایگزین جستجو می‌کنیم، باید والد آن را نیز بازگشت دهیم:

1private fun removeTwoChildNode(node: Node) {
2    val leftChild = node.left!!
3    leftChild.right?.let {
4        val maxParent = findParentOfMaxChild(leftChild)
5        maxParent.right?.let {
6            node.key = it.key
7            maxParent.right = null
8        } ?: throw IllegalStateException("Node with max child must have the right child!")
9    } ?: run {
10        node.key = leftChild.key
11        node.left = leftChild.left
12    }
13}

پیمایش

روش‌های مختلفی برای بازدید از گره‌ها وجود دارد. رایج‌ترین روش‌ها شامل روش «عمق-اول» (depth-first)، «عرض-اول» (breadth-first) و «سطح-اول» (level-first) است. در این مقاله ما تنها روش عمق-اول را بررسی می‌کنیم که می‌تواند یکی از حالت‌های زیر را داشته باشد:

1. پیش‌ ترتیبی (اول گره والد و سپس گره چپ و سپس گره راست را بازدید می‌کنیم)
2. میان‌ ترتیبی (ابتدا فرزند چپ، سپس گره والد و سپس فرزند راست را بازدید می‌کنیم)
3. پس‌ ترتیبی (ابتدا فرزند چپ را بازدید می‌کنیم و سپس فرزند راست و در نهایت گره والد)

برای کسب اطلاعات بیشتر درباره پیمایش درخت می‌توانید به مطلب آموزش پیمایش درخت در ساختمان داده به زبان ساده از مجله فرادرس مراجعه کنید.

همه انواع پیمایش در کاتلین می‌توانند به روشی ساده اجرا شوند. به عنوان نمونه برای پیمایش پیش‌ترتیبی می‌توان به صورت زیر استفاده کرد:

1fun visit(): Array<Int> {
2    val a = left?.visit() ?: emptyArray()
3    val b = right?.visit() ?: emptyArray()
4    return a + arrayOf(key) + b
5}

توجه کنید که کاتلین امکان الحاق آرایه‌ها را با استفاده عملگر + فراهم می‌سازد. البته این پیاده‌سازی فاصله زیادی با یک روش کارآمد دارد، چون tail-recursive نیست و در مورد درخت‌های با عمق زیاد ممکن است استثنای سرریز پشته را ایجاد کند.

سخن پایانی

در این راهنما با شیوه ساخت و پیاده‌سازی عملیات مقدماتی یک درخت جستجوی دودویی با استفاده از کاتلین آشنا شدیم. همچنین برخی سازه‌های کاتلین را که در جاوا موجود نیستند و می‌توانند مفید واقع شوند را معرفی کردیم. کد کامل این مطلب را می‌توانید در این صفحه گیت‌هاب (+) ملاحظه کنید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های جاوا (Java)
• مجموعه آموزش‌های برنامه‌‌نویسی
• برنامه نویسی Kotlin — مقدمه‌ای بر برنامه‌نویسی اندروید با زبان کاتلین
• برنامه نویسی Kotlin — ایجاد الگوهای طراحی اندروید با کاتلین
• درخت جستجوی دودویی (BST) — ساختار داده و الگوریتم ها

==